一、图论是什么?
图论是数学的一个分支,主要研究“图”的性质及其应用。图在现实世界中有着广泛的应用,比如网络、社交关系、交通路线、计算机科学中的各种结构等。
二、什么是“图”?
1. 图的定义
- 图(Graph)本质上是由一些点和点之间的连线组成的结构。
- 数学上,图常常表示为一个二元组:
G = (V, E)- V(Vertex set,点集):是图中所有“点”的集合。点也叫顶点或节点。
- E(Edge set,边集):是图中所有“边”的集合。边是连接两个顶点的线,可以理解为顶点之间的关系。
2. 例子
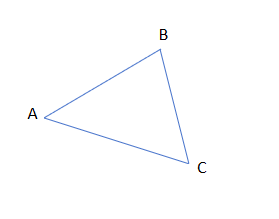
假设有三个点A、B、C:
- 点集V = {A, B, C}
- 边集E = { (A,B), (B,C) }
这里,(A,B)表示A和B之间有一条边,(B,C)表示B和C之间有一条边。
三、图的分类
1. 按点、边的数量
- 有限图:点集和边集都是有限个数的图。实际中大多数都是有限图。
- 无限图:点集、边集之一或全部是无限的图。主要在理论研究中涉及。
2. 按边的性质
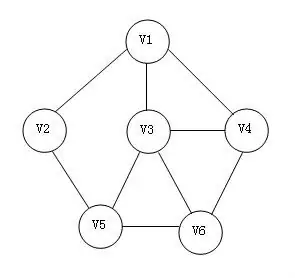
1)无向图(Undirected Graph)
- 边没有方向,连接的两个顶点地位对等。
- 用集合表示边,例如:{A,B} 表示A和B之间有边。
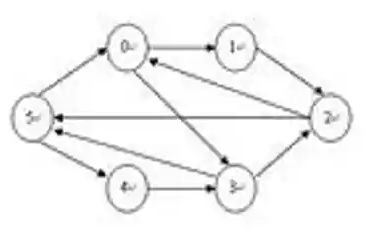
2)有向图(Directed Graph)
- 边有方向,从一个点指向另一个点。
- 用有序对表示边,例如:(A,B)表示从A指向B有一条边。
3)混合图(Mixed Graph)
- 既有有向边,也有无向边。
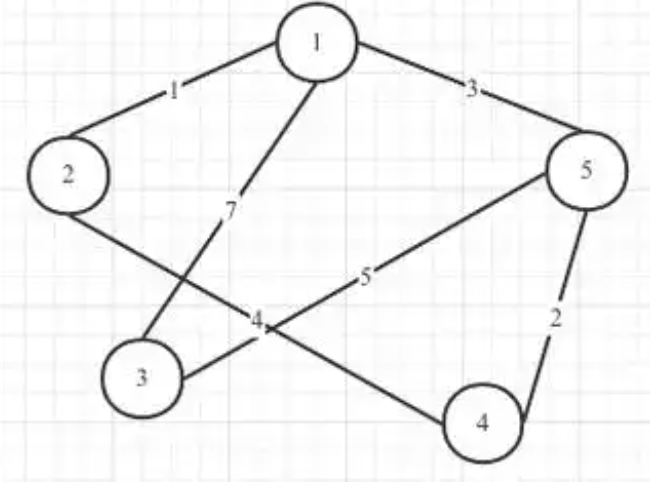
4)带权图(Weighted Graph)
- 边上有“权值”,比如距离、费用等。权值可以是任意数值,比如G=(V, E, w)表示w为权值函数。
四、图的表示方法
1、邻接矩阵(Adjacency Matrix)
(1)概念
邻接矩阵是一种二维数组,假设图有n个顶点,就用一个n×n的矩阵(数组)来表示顶点之间的连接关系。
- 行和列都代表顶点。
- 无向图:
matrix[i][j]=1表示节点i和j之间有边,否则为0。 - 有向图:
matrix[i][j]=1表示有一条从i指向j的边。
如果是带权图,则用权值(如距离、费用)代替1,未连接的地方可以用“无穷大”或-1等特殊值。
(2) 例子
假设有四个顶点A、B、C、D,编号为0,1,2,3。边如下:
- A连B(权重为2)
- A连C(权重为5)
- B连C(权重为4)
- C连D(权重为1)
邻接矩阵如下(无向带权图):
| 0(A) | 1(B) | 2(C) | 3(D) | |
|---|---|---|---|---|
| 0(A) | 0 | 2 | 5 | 0 |
| 1(B) | 2 | 0 | 4 | 0 |
| 2(C) | 5 | 4 | 0 | 1 |
| 3(D) | 0 | 0 | 1 | 0 |
如果是没有边的地方填 “无穷大”(inf):
| 0(A) | 1(B) | 2(C) | 3(D) | |
|---|---|---|---|---|
| 0(A) | 0 | 2 | 5 | inf |
| 1(B) | 2 | 0 | 4 | inf |
| 2(C) | 5 | 4 | 0 | 1 |
| 3(D) | inf | inf | 1 | 0 |
3. 优缺点
优点
- 查找两点是否有边,或边的权值,速度非常快,O(1)。
- 编码简单,适合用于小规模稠密图(边数接近n²)。
缺点
- 空间浪费大。n个点,不管有没有边都要n²个空间。
- 不方便遍历一个点所有相邻点(需要一行一行查)。
常用场景
- 点数不大(比如n<500),或者图比较稠密(边很多)。
- 需要频繁判断两点是否有边。
2、邻接表(Adjacency List)
(1) 概念
邻接表是用“每个点维护一个链表(或列表)”,存储它所有相邻的点。
- 一个数组,数组下标i代表顶点i。
- 每个i对应一个链表/列表,记录所有和i直接相连的点和权值。
(2) 例子
还是上面那4个点的例子:
邻接表表示如下:
0(A): [(1,2), (2,5)] // A连B权2,A连C权5
1(B): [(0,2), (2,4)] // B连A权2,B连C权4
2(C): [(0,5), (1,4), (3,1)] // C连A权5,连B权4,连D权1
3(D): [(2,1)] // D连C权1如果是无权图,可以只记录点编号,不带权值。
(3)优缺点
优点
- 空间效率高。只存实际存在的边,适合大多数稀疏图(边比较少)。
- 遍历某点的所有邻居很方便。
- 添加、删除边简单。
缺点
- 查找两点之间是否有边,时间复杂度是O(该点的度),不是O(1)。
- 编码略复杂,比邻接矩阵多一步初始化。
常用场景
- 点数大,但边数较少(稀疏图)。
- 需要遍历每个点的所有邻居,比如BFS、DFS等。
3、边集数组(Edge List)
(1)概念
边集数组就是一个数组,每个元素都是一条边(起点、终点、权值)。
(2)例子
用数组存储所有边:
[ (0, 1, 2), // A到B,权2
(0, 2, 5), // A到C,权5
(1, 2, 4), // B到C,权4
(2, 3, 1) // C到D,权1 ]每条边都用三元组(起点,终点,权值)表示。
(3)优缺点
优点
- 编码最简单,没什么结构,可以灵活处理。
- 非常适合需要遍历所有边的算法,比如Kruskal最小生成树。
缺点
- 不适合快速查找某一点的所有邻居。
- 查找两点之间是否有边,必须遍历整个数组,效率低。
常用场景
- 边为主的算法(如Kruskal、求边排序等)。
- 只关心边的整体属性,不关注单个点的邻居。
4、三种方法的简要对比
| 方法 | 空间复杂度 | 查找是否有边 | 遍历某点相邻点 | 适用场景 |
|---|---|---|---|---|
| 邻接矩阵 | O(n²) | O(1) | O(n) | 小规模稠密图 |
| 邻接表 | O(n+m) | O(度) | O(度) | 稀疏图常用 |
| 边集数组 | O(m) | O(m) | O(m) | 遍历所有边的情形 |
n为点数,m为边数。
五、图的基本术语
- 路径:从一个点走到另一个点经过的点和边的序列。
- 回路/环:起点和终点是同一个点的路径,且不重复经过其它点。
- 连通图:任意两点之间都能互达的图。
- 度(Degree):一个点连接的边数。
- 无向图:节点的度就是连接它的边数。
- 有向图:分为入度(进来的边数)和出度(出去的边数)。