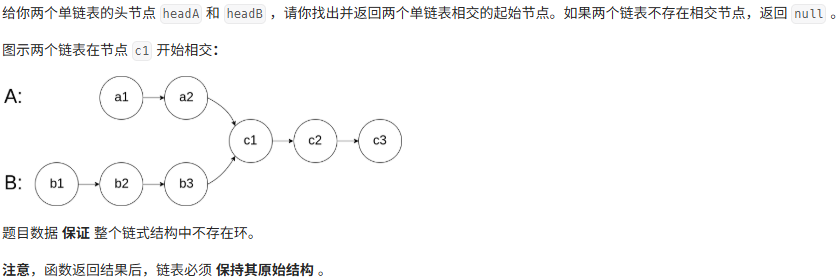
问题描述
核心思路:双指针交替遍历
算法思想: 使用两个指针 pa 和 pb 分别从链表A和链表B的头节点出发,同步向后遍历。当任一指针走到链表末尾时,将其重定位到另一链表的头节点继续遍历。若两链表相交,pa 和 pb 最终会在相交节点相遇;若不相交,则最终会同时到达 null。
数学原理: 设链表A独立部分长度为 a,链表B独立部分长度为 b,公共部分长度为 c。
- 指针
pa的路径:a + (b - c) + c = a + b - 指针
pb的路径:b + (a - c) + c = a + b两指针走过的总长度均为a + b,因此必然在相交节点(或null)相遇。
代码实现:
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA==null||headB==null){
return null;
}
ListNode pa=headA;
ListNode pb=headB;
while(pa!=pb){
if(pa==null){
pa=headB;
}else{
pa=pa.next;
}
if(pb==null){
pb=headA;
}else{
pb=pb.next;
}
}
return pa;
}复杂度分析:
- 时间复杂度:O(m + n),其中 m 和 n 分别为链表长度。
- 空间复杂度:O(1),仅使用两个指针。
关键点:
- 循环终止条件:
pa == pb时退出循环(包括两者均为null的情况)。 - 重定位时机:当指针走到当前链表末尾时,立即切换到另一链表的头部。
- 不相交处理:两指针最终同时为
null,返回null符合预期。
其他解法对比
方法二:计算长度差(同步遍历)
思路:
- 遍历两链表,分别计算长度
lenA和lenB。 - 长链表指针先走
|lenA - lenB|步。 - 两指针同步遍历,相遇点即为相交节点。
代码:
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int lenA = getLength(headA), lenB = getLength(headB);
ListNode pa = headA, pb = headB;
// 长链表指针先走差值步
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) pa = pa.nextB; i++) pa = pa.next;
} else {
for (int i = 0; i < lenB - lenA; i++) pb = pb.next;
}
// 同步遍历直至相遇
while (pa != pb) {
pa = pa.next;
pb = pb.next;
}
return pa;
}
private int getLength(ListNode head) {
int lenLength(ListNode head) {
int len = 0;
while (head != null) {
len++;
head = head.next;
}
return len;
}复杂度:
- 时间复杂度:O(m + n)(需两次遍历)。
- 空间复杂度:O(1)。
适用场景: 当链表长度差异较大时,此方法可能略快于双指针交替法。
方法三:哈希集合(空间换时间)
思路: 1时间) 思路:
- 遍历链表A,将所有节点存入
HashSet。 - 遍历链表B,检查节点是否在集合中,第一个存在的节点即为交点。
代码:
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set<ListNode> set = new HashSet<>();
while (headA != null) {
set.add(headA);
headA = headA.next;
}
while (headB != null) {
if (set.contains(headB)) return headB;
headB = headB.next;
}
return null;
}复杂度:
- 时间复杂度:O(m + n)。
- 空间复杂度:O(m)(存储链表A的节点)。
适用场景: 对空间复杂度不敏感时,代码最简洁直观。
方法对比总结
| 方法 | 时间复杂度 | 空间复杂度 | 特点 |
|---|---|---|---|
| 双指针交替遍历 | O(m + n) | O(1) | 空间最优,代码简洁 |
| 计算长度差 | O(m + n) | O(1) | 逻辑清晰,略多一次遍历 |
| 哈希集合 | O(m + n) | O(m) | 思路直接,但需额外空间 |
推荐:双指针交替遍历法在空间和代码简洁性上表现最佳,是面试中的理想解法。
问题描述
核心解法:迭代双指针法
算法思想: 使用双指针 new_head 和 temp 动态反转链表:
new_head:指向已反转部分的头节点(初始为null)temp:遍历原链表的当前节点 每次迭代将当前节点从原链表断开,插入到反转链表的头部,实现原地反转。
代码实现:
public ListNode reverseList(ListNode head) {
ListNode new_head = null;
ListNode temp = head;
while (temp != null) {
ListNode next = temp.next; // 保存后继节点
temp.next = new_head; // 当前节点指向反转链表头部
new_head = temp; // 更新反转链表头
temp = next; // 移动到下一个节点
}
return new_head;
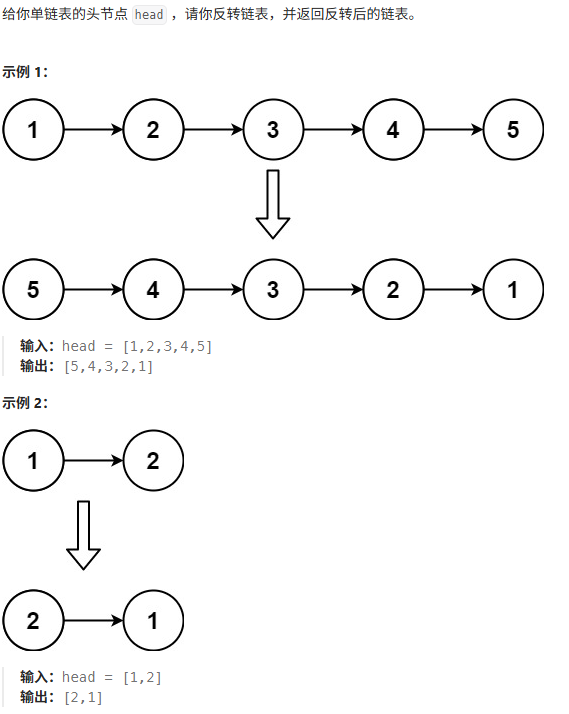
}图解过程:
原始链表:1 → 2 → 3 → 4 → null
迭代过程:
第1轮:new_head=1→null, temp=2
第2轮:new_head=2→1→null, temp=3
第3轮:new_head=3→2→1→null, temp=4
第4轮:new_head=4→3→2→1→null, temp=null复杂度分析:
- 时间复杂度:O(n),仅需一次遍历
- 空间复杂度:O(1),仅使用常量空间
优势:
- 原地操作,不占用额外空间
- 逻辑清晰,代码简洁
- 适用于所有编程语言的链表实现
其他经典解法
方法二:递归法(分治思想)
算法思想:
- 递归到链表尾部
- 回溯时反转节点指向
- 返回新的头节点
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next); // 递归到尾部
head.next.next = head; // 反转指针方向
head.next = null; // 断开原指针
return newHead;
}复杂度分析:
- 时间复杂度:O(n)
- 空间复杂度:O(n)(递归栈空间)
适用场景:
- 链表长度适中(避免栈溢出)
- 需要简洁的代码表达
- 函数式编程环境
方法三:头插法(使用虚拟节点)
算法思想:
- 创建虚拟头节点
dummy - 遍历原链表,将每个节点插入到
dummy之后 - 返回
dummy.next
public ListNode reverseList(ListNode head) {
ListNode dummy = new ListNode(-1);
ListNode cur = head;
while (cur != null) {
ListNode next = cur.next; // 保存后继节点
cur.next = dummy.next; // 头插操作
dummy.next = cur; // 更新头节点
cur = next; // 移动指针
}
return dummy.next;
}复杂度分析:
- 时间复杂度:O(n)
- 空间复杂度:O(1)
优势:
- 统一处理头节点特殊情况
- 逻辑更易理解
- 支持链表的其他变形操作
方法对比总结
| 方法 | 时间复杂度 | 空间复杂度 | 特点 |
|---|---|---|---|
| 迭代双指针 | O(n) | O(1) | 空间最优,推荐首选 |
| 递归法 | O(n) | O(n) | 代码简洁,但空间消耗大 |
| 头插法(虚拟节点) | O(n) | O(1) | 逻辑清晰,易扩展 |
核心技巧:
- 指针保存:在修改节点指针前,必须保存后继节点引用
- 头插操作:将节点插入链表头部是反转的关键
- 终止条件:注意处理空链表和单节点链表的边界情况
延伸思考:
- 如何反转部分链表(区间反转)?
- 如何K个一组反转链表?
- 如何判断链表是否有环?(快慢指针技巧)
迭代双指针法因其优异的时空复杂度,成为面试和工程实践中的首选方案。掌握这三种经典解法,能够灵活应对各种链表反转问题。