D. 2+ doors
题目: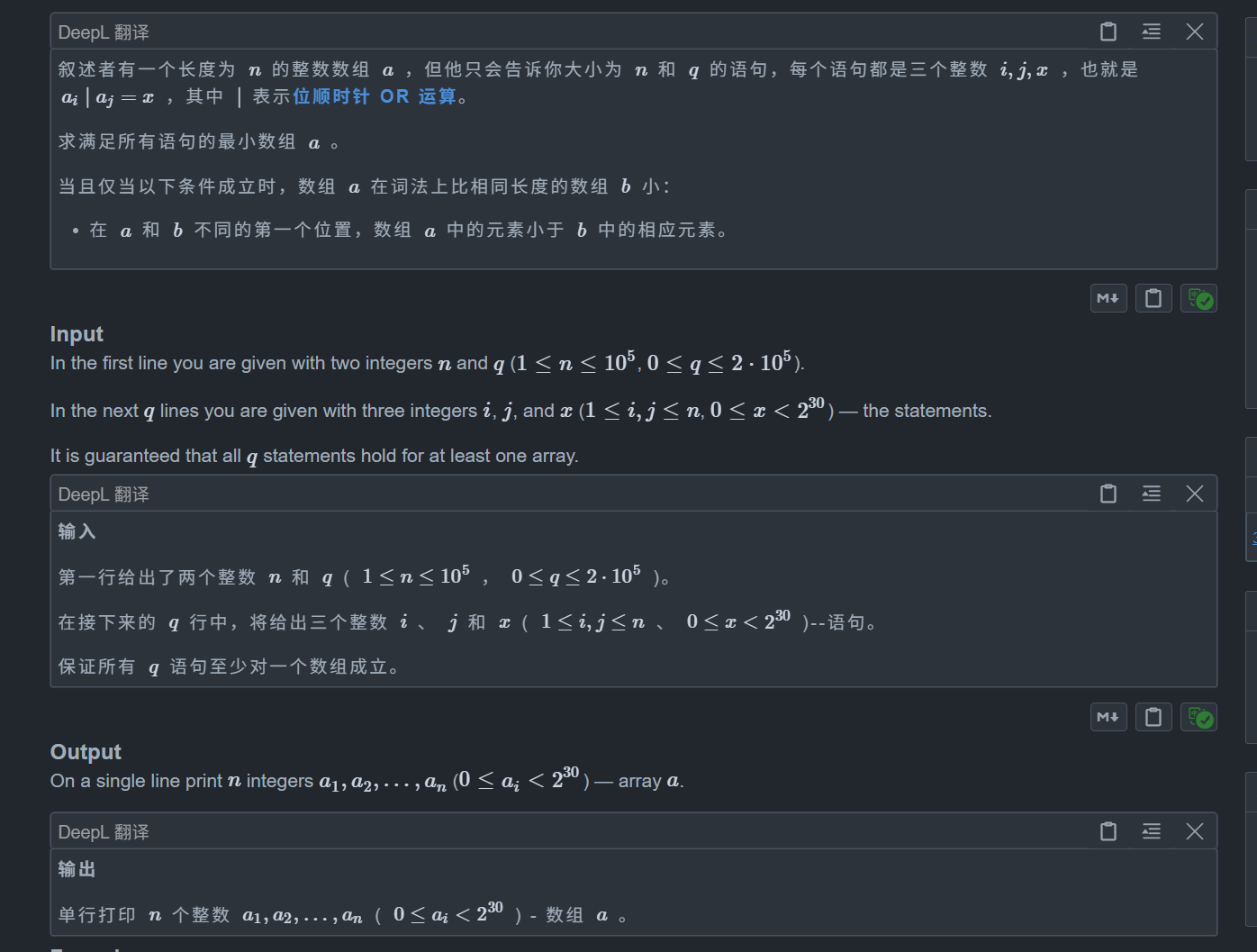
思路:
有多种解法,这里选了一个稍微好理解的解法
题目的条件给的很简单,给你 q 个限制,在确保 a[i] | a[j] = x 的限制下构造出字典序最小的数组 a
显然我们可以分位考虑,因为每个位都是不影响的,那么考虑如何构造
假如 a[i] | a[j] = x 中某一位是 0,那么 a[i] 和 a[j] 这一位就必须都是 0,否则如果是 1,那么二者可以任意一个这一位是 1 另一个是 0,但是当 i = j 时,a[i] 这一位就必须是 1 了
我们定义 must0[i][j] 为 a[i] 的第 j 位是否必须为 0,如果 must0[i][j] = 1,则这位只能是 0,must1[i][j] 同理
然后考虑建图,由于有其中一个是 0 一个是 1 的情况,那么显然我们可以让下标小的那个数为 0,所以定义 g[i][j] 其中储存着当 i 的第 j 位为 0 时有哪些下标的该位必须为 1
随后就直接暴力模拟即可,具体实现可以看代码,还是很好理解的
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int must0[100005][30], must1[100005][30];
// 当 i 的第 j 位为 0 时其孩子必须为 1
vector<vector<vector<int>>> g(100005, vector<vector<int>>(30));
void solve()
{
int n, q;
cin >> n >> q;
while (q--)
{
int i, j, x;
cin >> i >> j >> x;
if (i > j)
swap(i, j);
for (int w = 0; w < 30; w++)
{
if (x >> w & 1)
{
if (i == j)
must1[i][w] = 1;
else
g[i][w].push_back(j);
}
else
{
must0[i][w] = must0[j][w] = 1;
}
}
}
for (int i = 1; i <= n; i++)
{
int res = 0;
for (int w = 0; w < 30; w++)
{
if (must0[i][w])
{
for (auto &son : g[i][w])
{
must1[son][w] = 1;
}
continue;
}
int flag = must1[i][w];
for (auto &son : g[i][w])
{
if (must0[son][w])
flag = 1;
}
if (!flag)
{
for (auto &son : g[i][w])
{
must1[son][w] = 1;
}
}
else
{
res |= 1 << w;
}
}
cout << res << " ";
}
cout << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
while (t--)
{
solve();
}
return 0;
}C. Min-Max Array Transformation
题目:
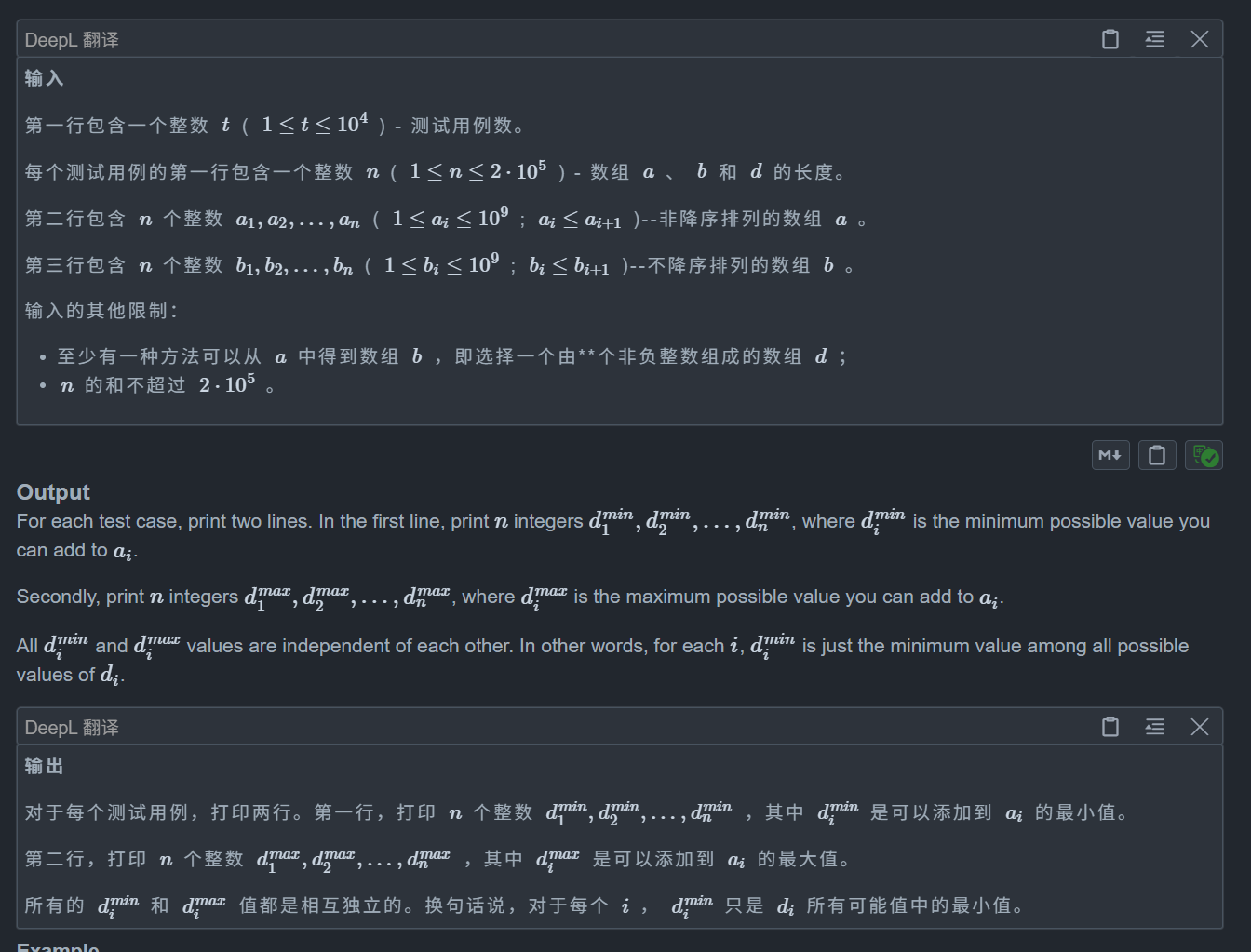 思路:
思路:
感觉有点难想
不难发现 d_min 是很简单的,我们直接在 b 中找到第一个小于等于 a[i] 的下标即可,则有 d_min = b[it] - a[i]
但是 d_max 略显复杂,我们画图理解一下
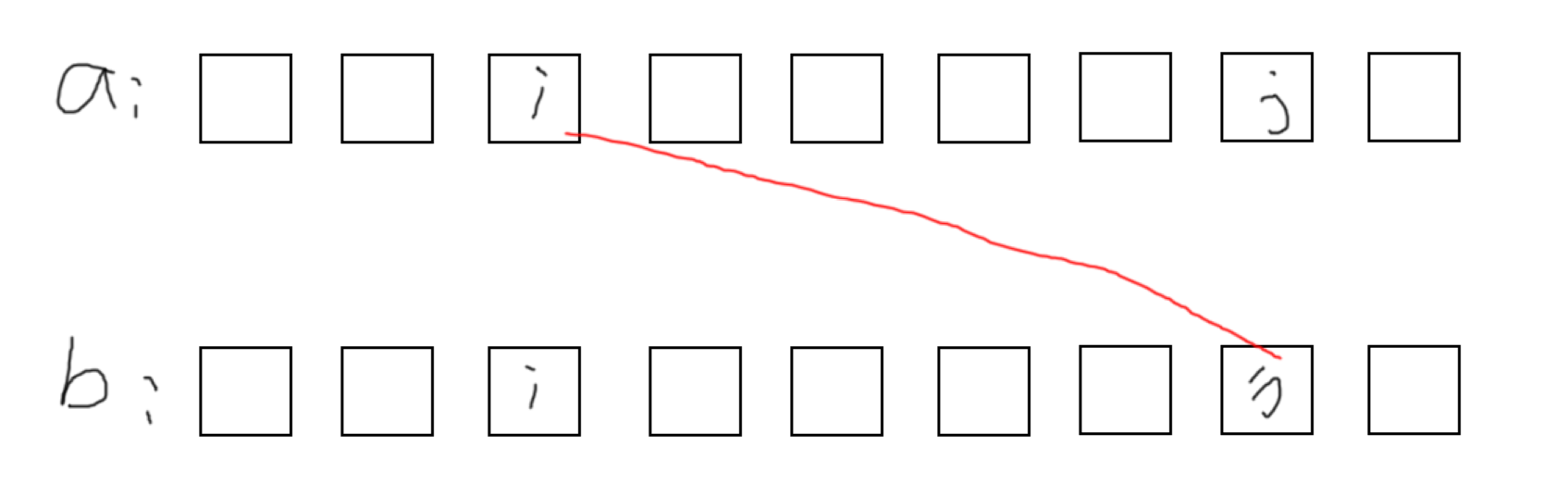
假设我们的 a[i] 选了 j 这个位置,那么 i ~ j 的位置就需要重新排列了,考虑最极限情况,即
为什么呢?因为我们两个数组都是递增的,所以选择相邻的比较肯定是最好的,否则如果往前选,那么配对失败的概率越高
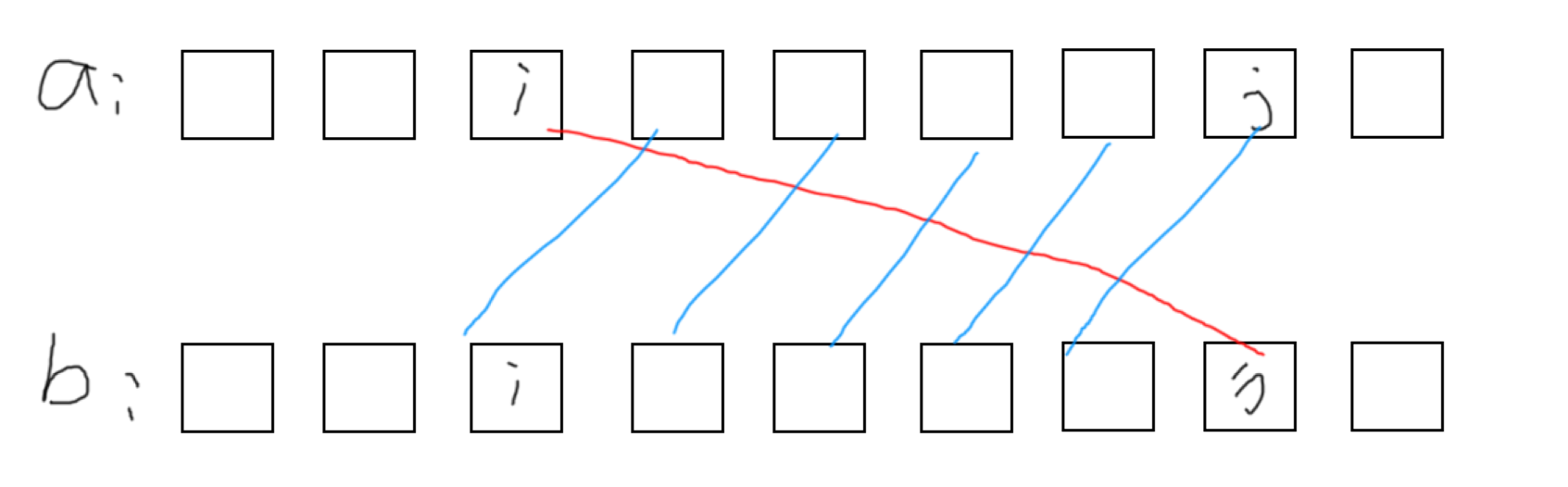
那为什么不用管其余位置呢?显然其余位置直接配对即可
那为什么 j 不往右边选呢?显然如果选了右边的,那么 j + 1 就面临着 j 的同样情况,所以显然不行
所以我们显然现在的目标就是找到一个点 j,使得对于每一个 k,都有 b[k-1] >= a[k],如何去找呢?
我们不妨考虑倒序枚举,一开始 j 为 n,那么显然当某个点 i 的 d_min 的位置也是 i 时就不行了,因为此时就如下图了
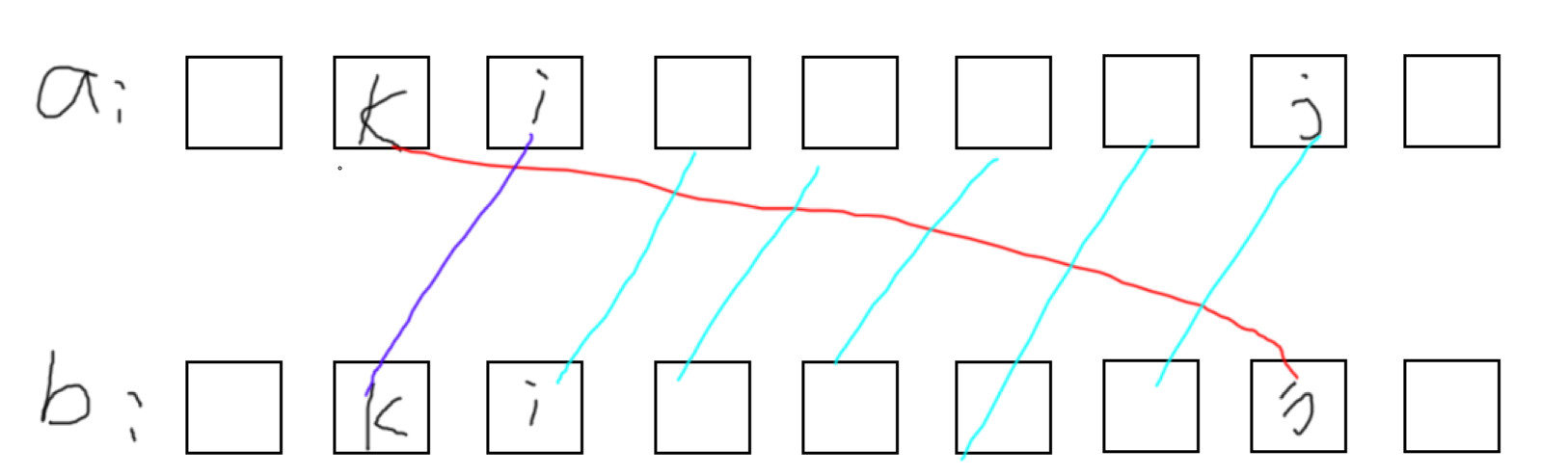
此时紫线配对是不成立的,因此此时就要更新 j 了
具体实现看代码
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
void solve()
{
int n;
cin >> n;
vector<int> a(n), b(n), mi(n), mx(n);
for (int i = 0; i < n; i++)
cin >> a[i];
for (int i = 0; i < n; i++)
cin >> b[i];
int j = n - 1;
for (int i = n - 1; i >= 0; i--)
{
auto it = lower_bound(b.begin(), b.end(), a[i]) - b.begin();
mi[i] = b[it] - a[i];
mx[i] = b[j] - a[i];
if (it == i)
{
j = i - 1;
}
}
for (int i = 0; i < n; i++)
cout << mi[i] << " ";
cout << endl;
for (int i = 0; i < n; i++)
cout << mx[i] << " ";
cout << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}D. Madoka and The Corruption Scheme
题目: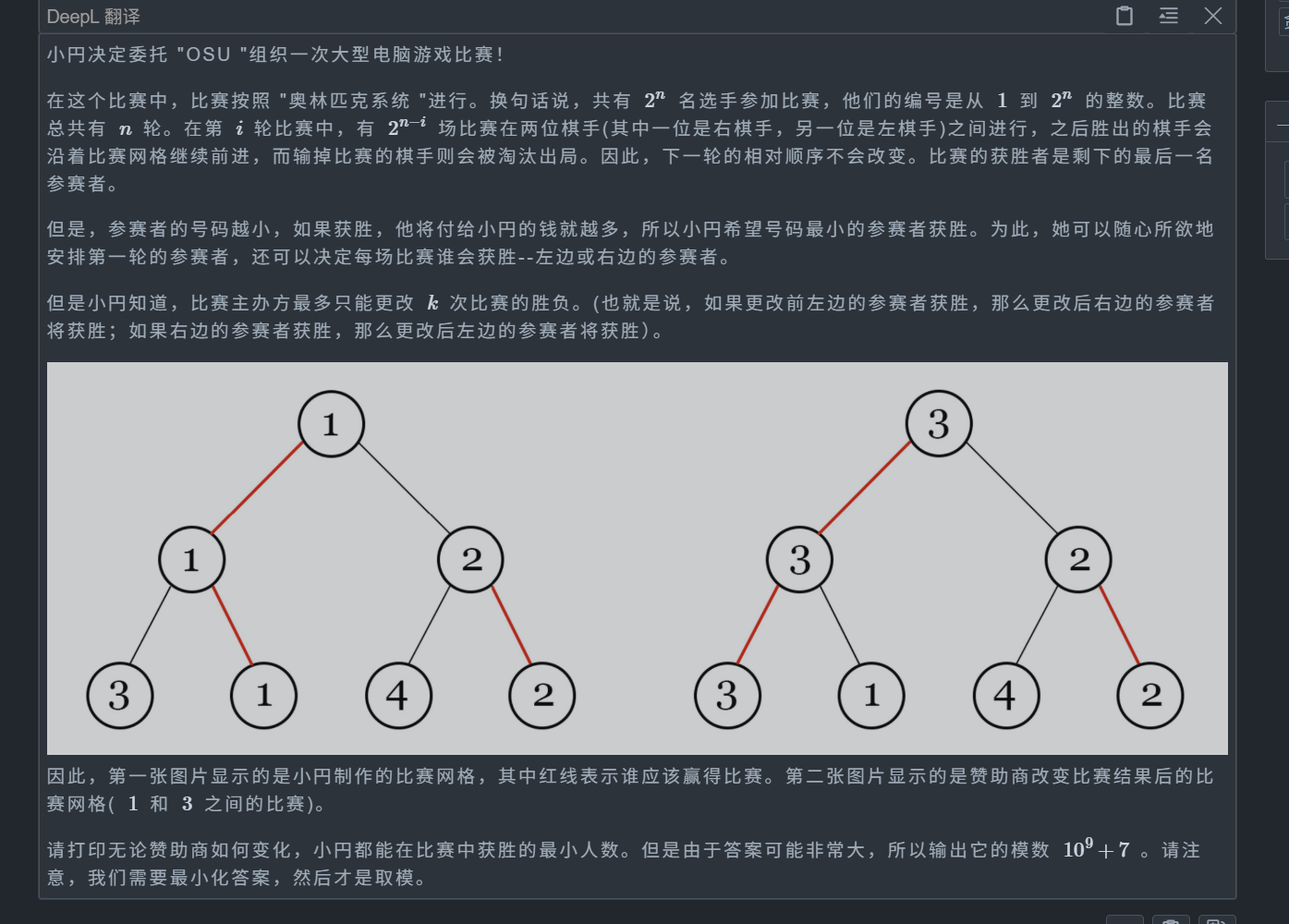
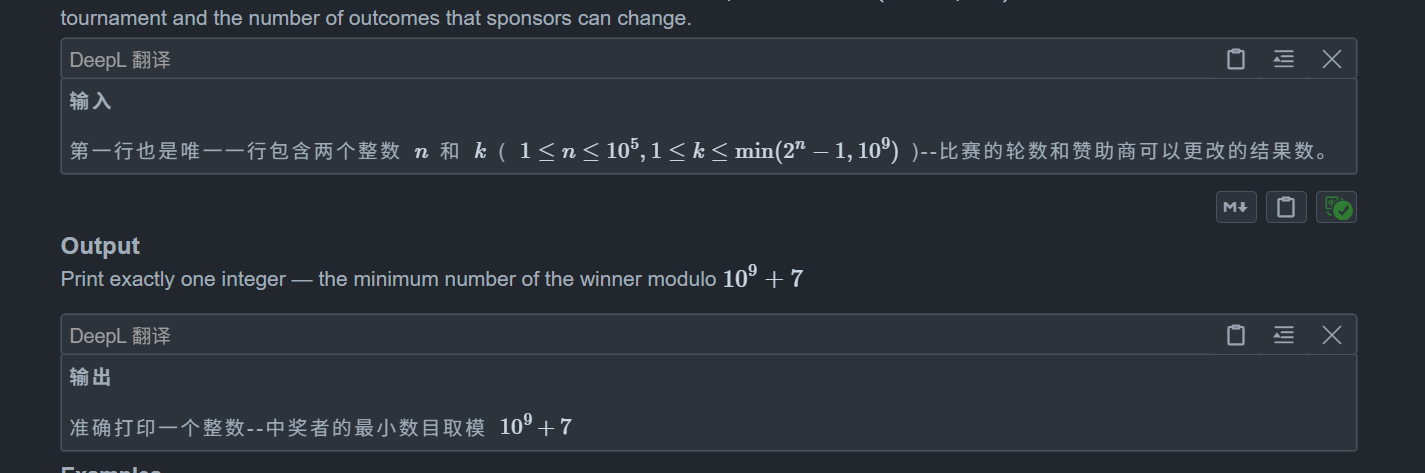 思路:
思路:
转换为数学问题
题目乍一看一点都不知道怎么写,我们不妨先考虑左线全胜利,那么就是下图所示
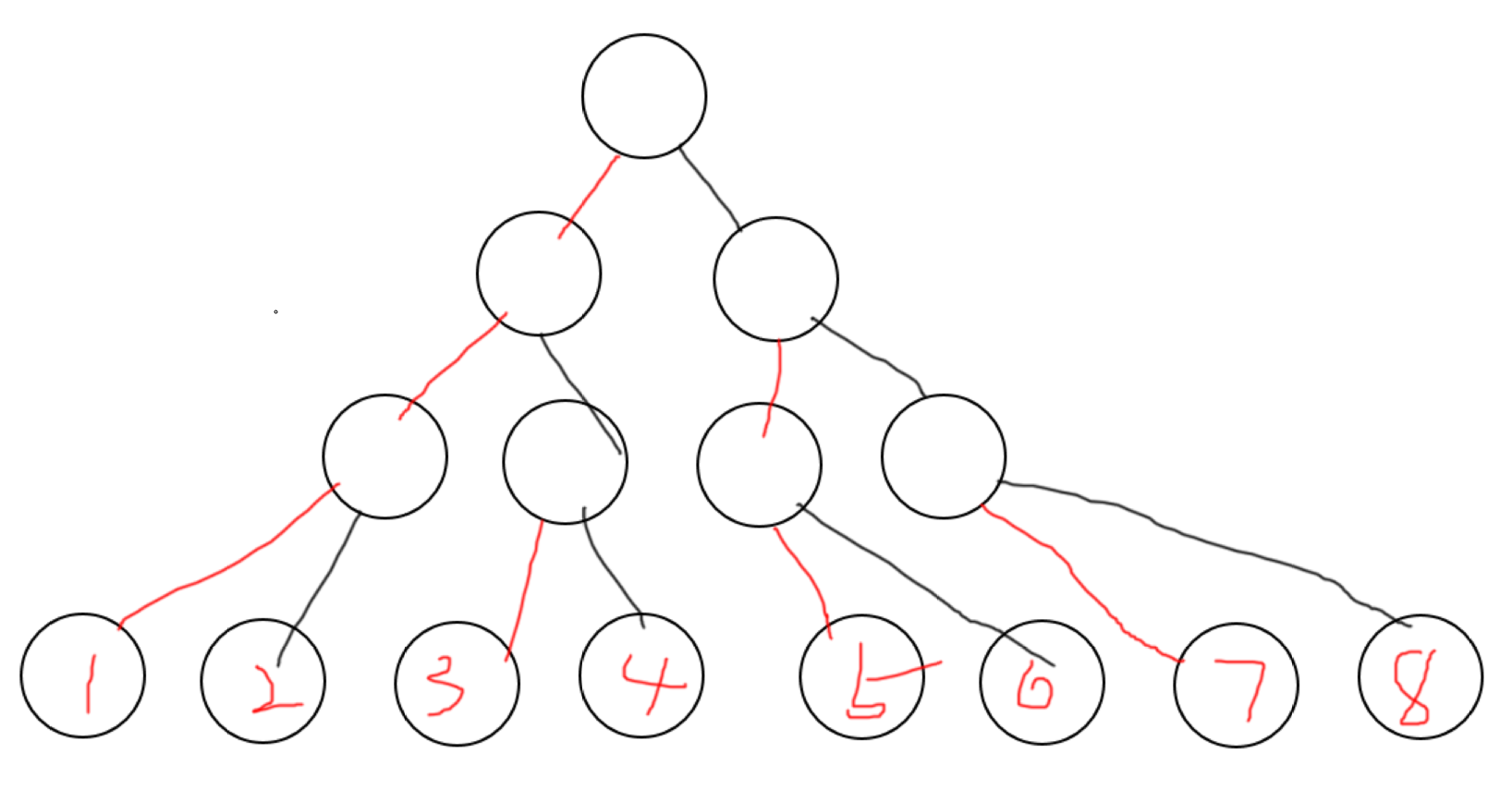
那么我们考虑最后获胜的人有什么特点,不难发现,如果一个数 x 能走 n 次红边,那么就能获胜
那么现在我能将 k 条边重新定向,我们不妨考虑 3节点 要赢差几条边,显然就差一条,所以 3 节点只需要 一次 重新定向即可,我们定义 f[i] 为需要修改 i 次才能获胜的节点数量,不难发现其就等于
所以我们只需要求 0 ~ min(k,n) 的 即可,假设求出来的结果为 sum,也就是说在修改 k 条边的情况下能强行使得 sum 个节点获胜,那么为了小的获胜,我们将 1 ~ sum 分给这 sum 个节点即可,所以最后结果就是 sum
具体实现看代码
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
const int MOD = 1e9 + 7;
int fac[100005], inv_fac[100005];
int qp(int a, int b)
{
int res = 1;
a %= MOD;
while (b)
{
if (b & 1)
res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
int C(int n, int m)
{
return fac[m] * inv_fac[n] % MOD * inv_fac[m - n] % MOD;
}
void solve()
{
int n, k;
cin >> n >> k;
fac[0] = 1;
for (int i = 1; i <= n; ++i)
fac[i] = fac[i - 1] * i % MOD;
inv_fac[n] = qp(fac[n], MOD - 2);
for (int i = n - 1; i >= 0; i--)
inv_fac[i] = inv_fac[i + 1] * (i + 1) % MOD;
int ans = 0;
for (int i = 0; i <= min(n, k); i++)
{
ans = (ans + C(i, n)) % MOD;
ans = (ans + MOD) % MOD;
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
while (t--)
{
solve();
}
return 0;
}D1. Xor-Subsequence (easy version)
题目:
 思路:
思路:
题意真的很麻烦,为什么不能说人话
题目大意:
让你求一个 a 的最长的子序列 b,其中 b 需要满足任意两个相邻的元素都要满足 a[i] ^ j < a[j] ^ i,其中 j > i
那么显然可以按照 LIS 的思想直接双重枚举,对于 dp[i] 就有 dp[i] = max{ dp[j] + 1 },其中 j < i,且 a[j] ^ i < a[i] ^ j
但是对于 n 这个 1e5 数据显然会爆,不妨观察到题目中的 a[i] 很小只有 200,再看到转移条件中的异或操作,不难想到我们最多只能改变 a[i] 的二进制的八位,所以 j 其实不用从 0 开始枚举,只需要从 i - 256 开始枚举即可
然后就是套 LIS 即可,具体实现看代码
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
void solve()
{
int n;
cin >> n;
vector<int> a(n);
vector<int> dp(n, 1);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int mx = 0;
for (int i = 0; i < n; i++)
{
for (int j = max(i - 256, 0LL); j < i; j++)
{
if ((a[j] ^ i) < (a[i] ^ j))
{
dp[i] = max(dp[i], dp[j] + 1);
}
}
mx = max(dp[i], mx);
}
cout << mx << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}