排序算法是计算机科学的基础支撑,广泛应用于数据处理、检索优化等场景。本文将聚焦四种常用内部排序算法,剥离具体实例,从核心思想、算法流程、关键特性三个维度进行梳理,帮助快速掌握其本质逻辑。
一、排序算法基础概念
在深入具体算法前,需先明确两个核心分类:
- 内部排序:整个排序过程无需访问外存,仅在内存中完成,适用于数据量较小的场景(如本文涉及的四种算法均属此类)。
- 外部排序:待排序数据量极大,无法全部载入内存,需借助外存(如磁盘)配合内存完成排序,适用于大规模数据场景。
二、四种常用内部排序算法详解
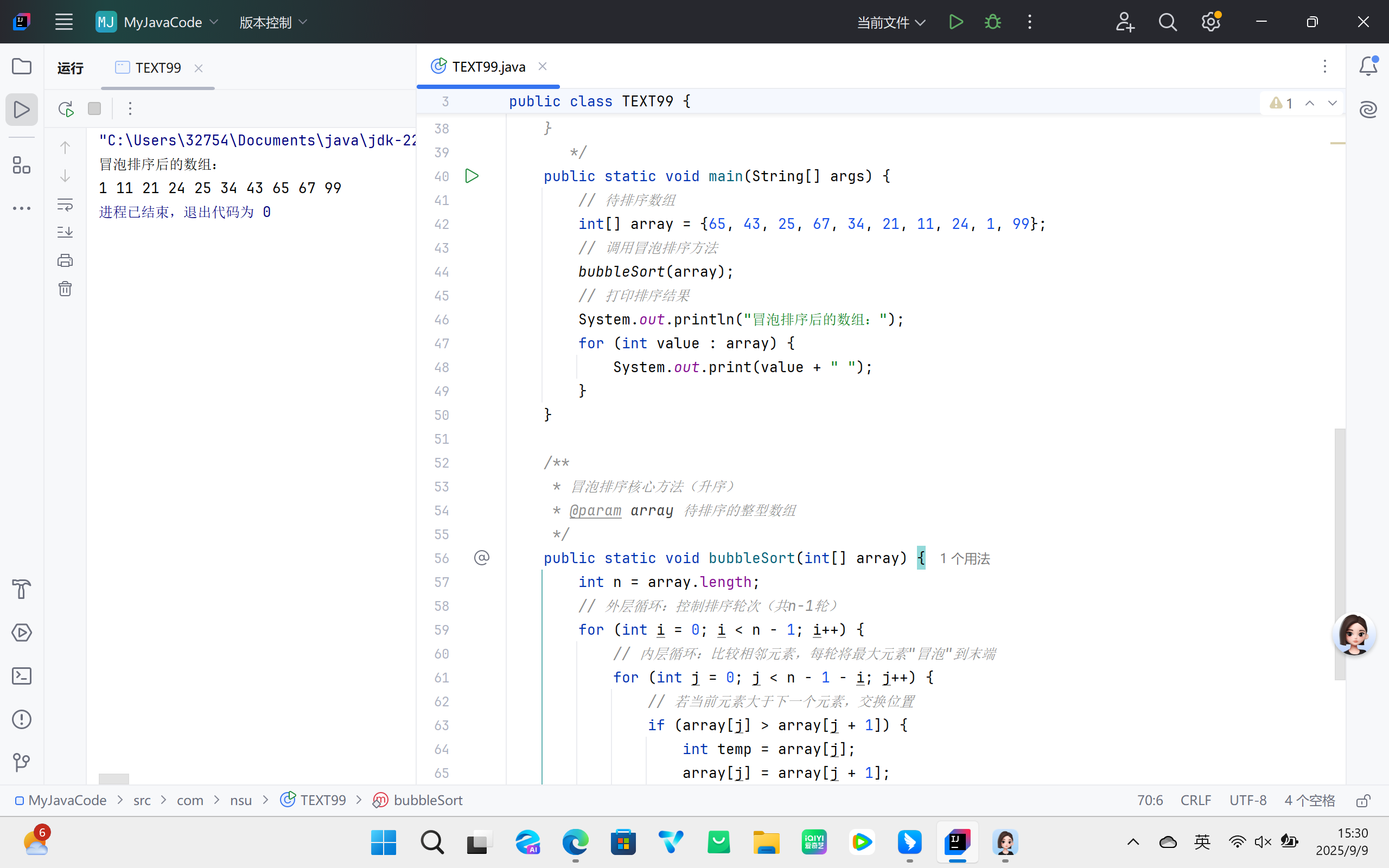
(一)冒泡排序
1. 核心思想
通过反复比较相邻元素的关键字,若发现逆序(前一个元素大于后一个元素,针对升序排序)则交换位置,逐步将最大元素 “冒泡” 至数组末端,直至整个数组有序。
2. 算法流程
- 初始化数组,设定外层循环控制排序轮次(共需
n-1轮,n为数组长度); - 内层循环遍历未排序区域,依次比较相邻元素,逆序则交换;
- 每完成一轮外层循环,未排序区域长度减 1(末端已确定一个最大元素);
- 重复上述步骤,直至外层循环结束,数组排序完成。
3. 关键特性
- 稳定性:稳定(相等元素的相对位置不会因排序改变);
- 时间复杂度:最佳情况
O(n)(已排序数组),最坏及平均情况O(n²); - 空间复杂度:
O(1)(仅需常数级临时变量)。
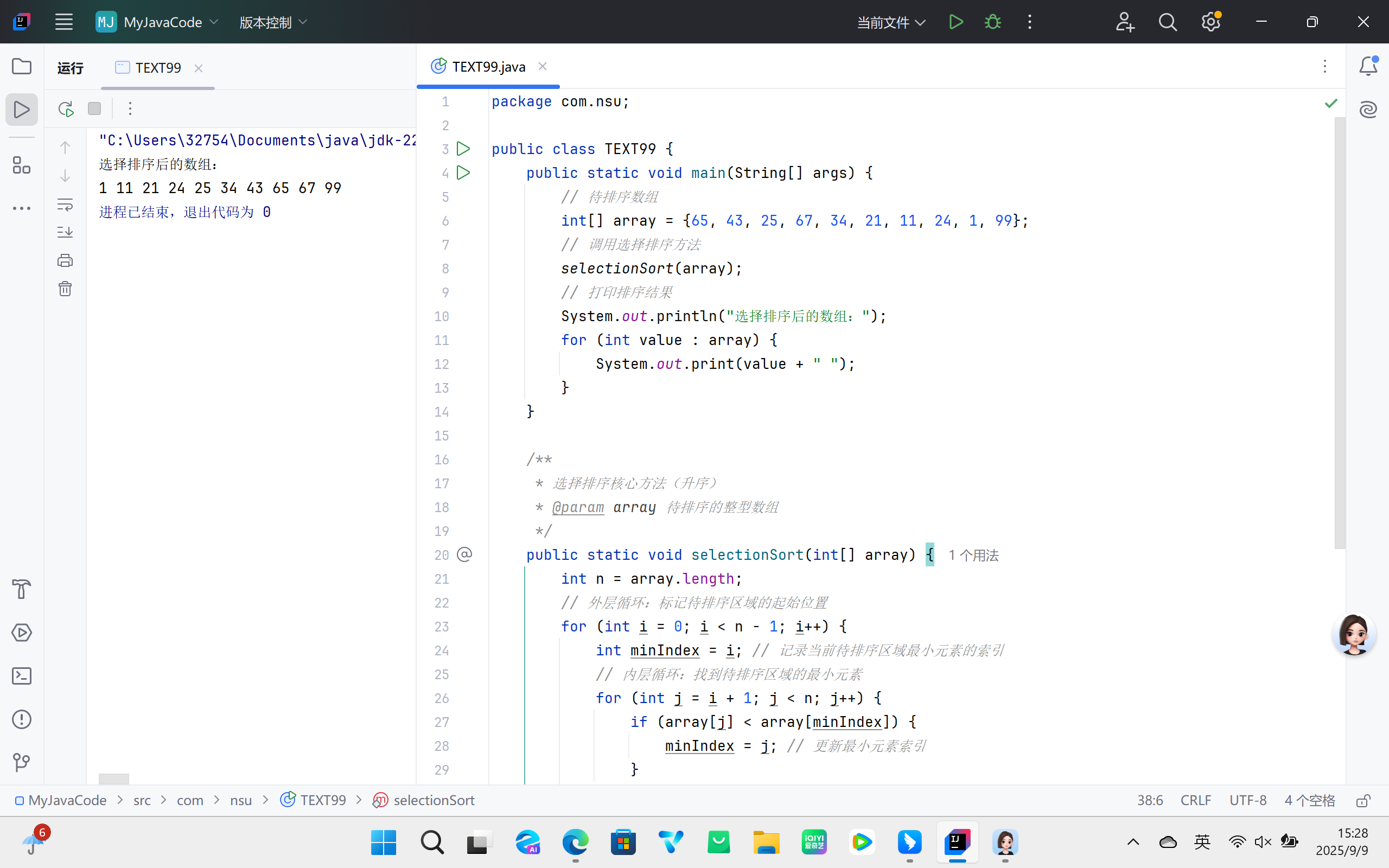
(二)选择排序
1. 核心思想
可视为冒泡排序的优化,通过 “选择” 而非 “交换” 减少操作次数:每轮从待排序区域中找到最小(或最大)元素,将其与待排序区域的起始位置交换,逐步缩小待排序区域范围,直至数组有序。
2. 算法流程
- 初始化数组,设定外层循环标记待排序区域的起始位置(从 0 到
n-2); - 内层循环遍历待排序区域,找到最小元素的索引;
- 若最小元素索引与待排序区域起始位置不同,则交换两位置元素;
- 外层循环后移一位,缩小待排序区域,重复步骤 2-3,直至数组有序。
3. 关键特性
- 稳定性:不稳定(可能改变相等元素的相对位置);
- 时间复杂度:最佳、最坏及平均情况均为
O(n²)(无论数组初始状态,均需完整遍历找最小元素); - 空间复杂度:
O(1)(仅需常数级临时变量及索引变量)。
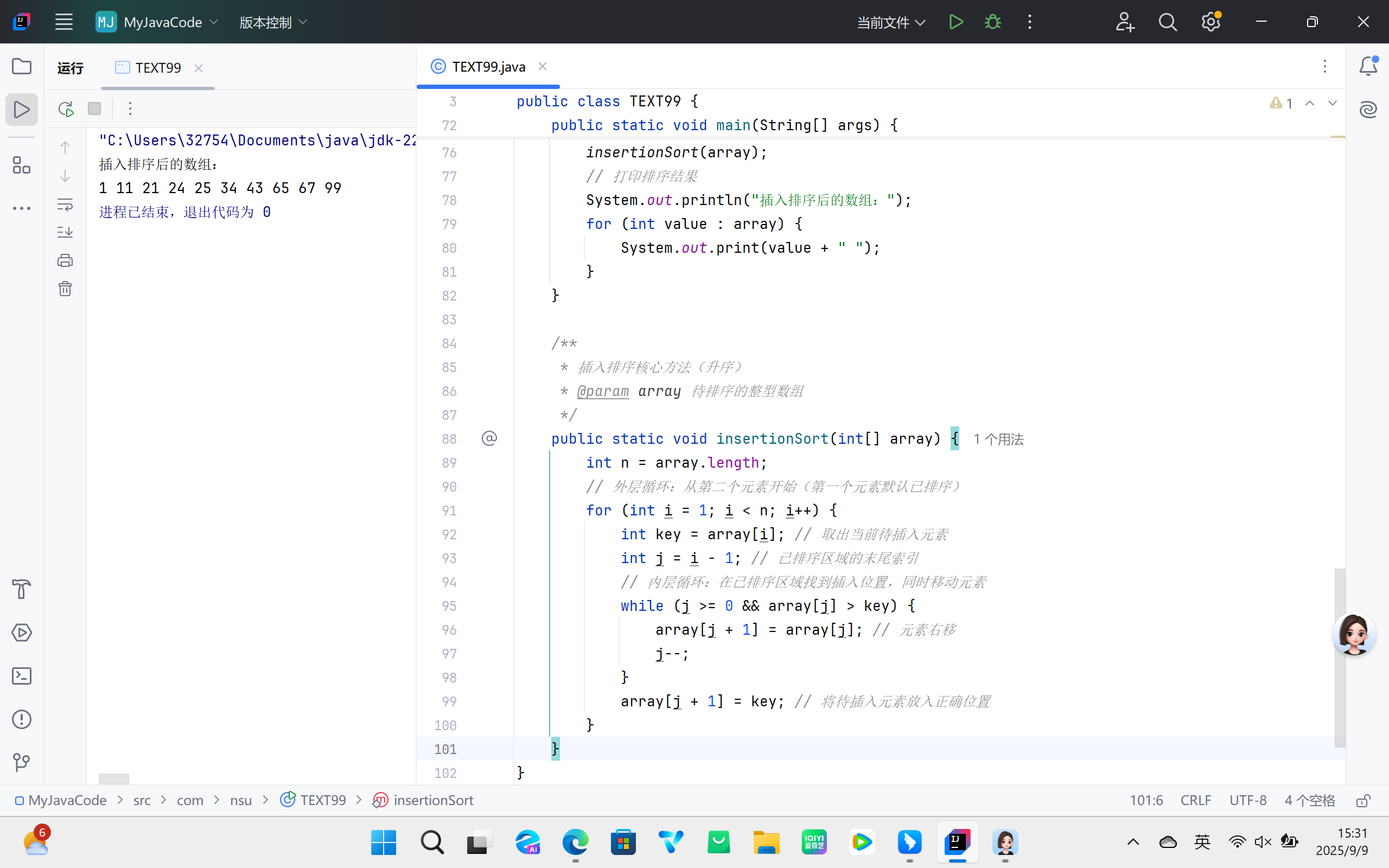
(三)插入排序
1. 核心思想
将数组分为 “已排序区域” 和 “未排序区域”,依次从无排序区域中取出元素,在已排序区域中从后向前扫描,找到合适插入位置并插入,同时将插入位置后的已排序元素右移腾出空间。
2. 算法流程
- 初始化时,将数组第一个元素视为已排序区域,其余为未排序区域;
- 外层循环从第二个元素开始,依次取出未排序区域的元素作为 “待插入元素”;
- 内层循环在已排序区域中从后向前比较,若已排序元素大于待插入元素,则将其右移;
- 找到待插入位置后,将待插入元素放入该位置;
- 外层循环后移,重复步骤 2-4,直至未排序区域为空。
3. 关键特性
- 稳定性:稳定;
- 时间复杂度:最佳情况
O(n)(已排序或接近有序数组),最坏及平均情况O(n²); - 空间复杂度:
O(1)(仅需常数级临时变量存储待插入元素); - 适用场景:小规模数组或部分有序数组(性能优于冒泡和选择排序)。
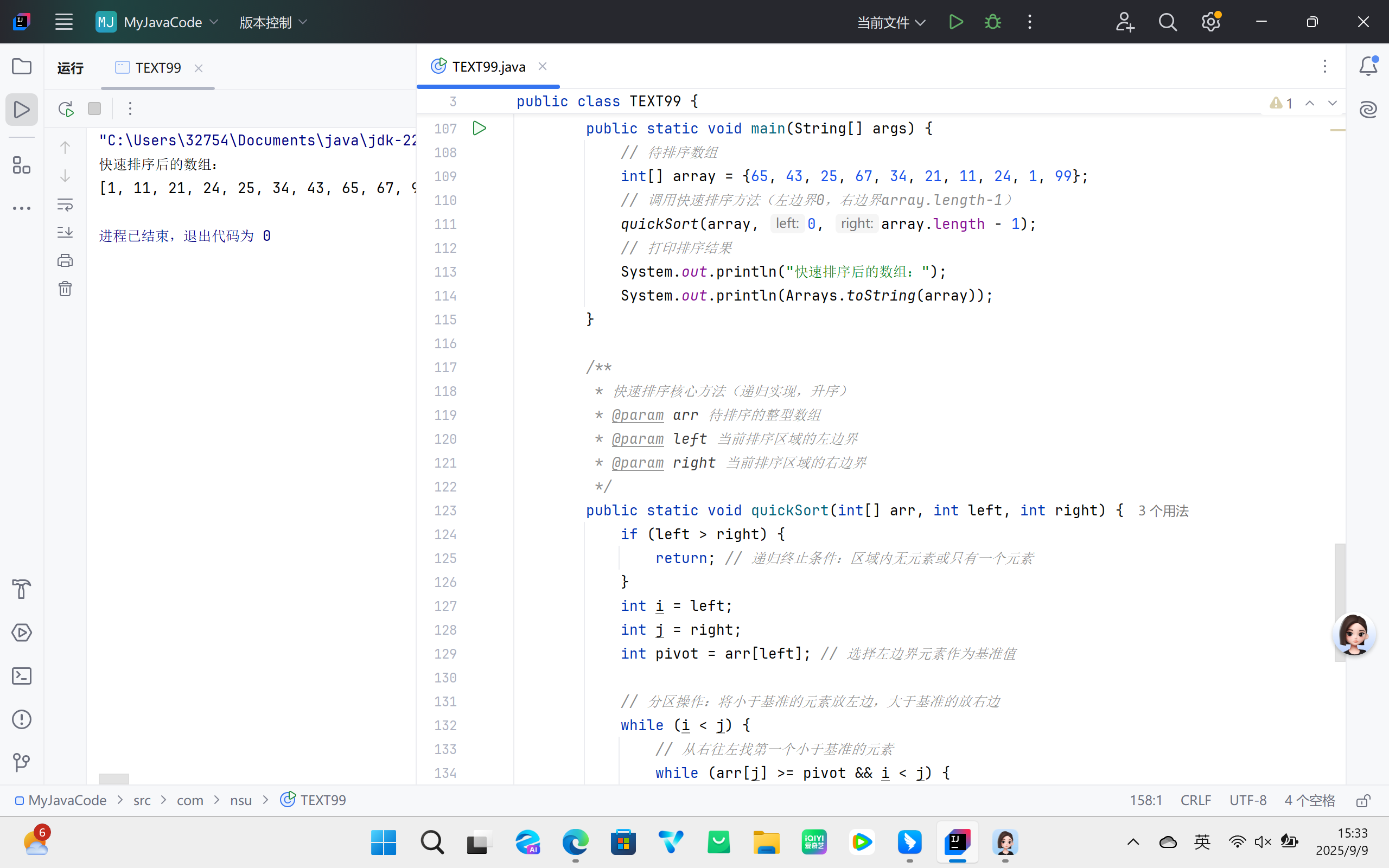
(四)快速排序
1. 核心思想
基于 “分治法”,通过一趟 “分区” 操作将数组分为两部分:左部分元素均小于等于 “基准元素”,右部分元素均大于等于基准元素;随后递归对左右两部分重复分区操作,直至子数组长度为 1(天然有序),最终实现整个数组有序。
2. 算法流程
- 选择数组中一个元素作为基准元素(通常选第一个或最后一个元素);
- 初始化两个指针
i(左指针,指向数组起始位置)和j(右指针,指向数组末尾位置); - 分区操作:先移动右指针
j找到第一个小于基准元素的值,再移动左指针i找到第一个大于基准元素的值,交换两指针指向的元素;重复此过程,直至i与j相遇; - 将基准元素与
i(j)指向的元素交换,完成分区(基准元素归位,左侧均≤基准,右侧均≥基准); - 递归对基准元素左侧子数组和右侧子数组执行步骤 1-4,直至所有子数组有序。
3. 关键特性
- 稳定性:不稳定;
- 时间复杂度:最佳及平均情况
O(nlogn),最坏情况O(n²)(数组已排序且选两端元素为基准时); - 空间复杂度:
O(logn)(递归调用栈开销,最佳情况)至O(n)(最坏情况); - 适用场景:大规模数组(平均性能优于冒泡、选择、插入排序)。
三、四种算法核心特性对比
为方便快速选型,下表汇总四种算法的核心差异:
| 算法 | 稳定性 | 最佳时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 核心优势 |
|---|---|---|---|---|---|---|
| 冒泡排序 | 稳定 | O(n) | O(n²) | O(n²) | O(1) | 实现简单,适用于小规模数据 |
| 选择排序 | 不稳定 | O(n²) | O(n²) | O(n²) | O(1) | 交换次数少,实现简单 |
| 插入排序 | 稳定 | O(n) | O(n²) | O(n²) | O(1) | 对部分有序数组性能优异 |
| 快速排序 | 不稳定 | O(nlogn) | O(n²) | O(nlogn) | O(logn)-O(n) | 大规模数组平均性能最优 |