前言
决策树是一种常用的机器学习模型,用于分类和回归任务,它通过模拟“树”的结构来对数据进行决策。本节我们详细讨论的是决策树中的分类任务
开始探索
scikit-learn
假设以下运维场景
- CPU
- 低:<40%
- 中:40%~70%
- 高:>70%
- 内存
- 低:<60%
- 中:60%~85%
- 高:>85%
- 磁盘I/O
- 低:<40%
- 中:40%~70%
- 高:>70%
- 日志报错数(条)
- 少:<20
- 中:20~50
- 多:>50
| CPU | 内存 | 磁盘I/O | 日志报错数 | 系统是否稳定 |
|---|---|---|---|---|
| 低 | 低 | 低 | 少 | 稳定 |
| 中 | 中 | 低 | 少 | 稳定 |
| 低 | 中 | 高 | 少 | 稳定 |
| 低 | 低 | 低 | 多 | 不稳定 |
| 低 | 低 | 高 | 中 | 不稳定 |
| 高 | 搞 | 低 | 少 | 不稳定 |
| 中 | 高 | 低 | 中 | 稳定 |
| 高 | 低 | 低 | 多 | 不稳定 |
| 中 | 高 | 高 | 少 | 不稳定 |
| 中 | 中 | 中 | 中 | 不稳定 |
| 高 | 高 | 低 | 少 | 稳定 |
将其转换成代码:
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
level_map = {'低': 0, '中': 1, '高': 2, '少': 0, '中': 1, '高': 2, '多':2, '稳定': 1, '不稳定': 0}
data = [
['低', '低', '低', '少', '稳定'],
['中', '中', '低', '少', '稳定'],
['低', '中', '高', '少', '稳定'],
['低', '低', '低', '多', '不稳定'],
['低', '低', '高', '多', '不稳定'],
['高', '高', '低', '少', '不稳定'],
['中', '高', '低', '中', '稳定'],
['高', '低', '低', '多', '不稳定'],
['中', '高', '高', '少', '不稳定'],
['中', '中', '中', '中', '不稳定'],
['高', '高', '低', '少', '稳定'],
]
data_mapped = [[level_map[v] for v in row] for row in data]
df = pd.DataFrame(data_mapped, columns=['CPU', '内存', '磁盘IO', '日志报错数', '系统是否稳定'])
X = df[['CPU', '内存', '磁盘IO', '日志报错数']]
y = df['系统是否稳定']
clf = DecisionTreeClassifier(criterion='entropy', random_state=0)
clf.fit(X, y)
y_pred = clf.predict(X)
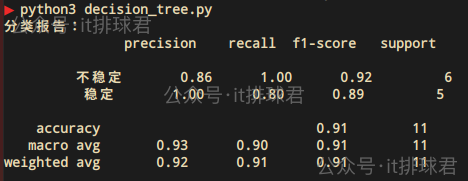
print("分类报告:\n", classification_report(y, y_pred, target_names=['不稳定', '稳定']))
脚本!启动
绘图更能直接观察决策树
from sklearn import tree
import matplotlib.pyplot as plt
plt.figure(figsize=(14, 8))
tree.plot_tree(clf,
feature_names=['CPU', 'memory', 'storage I/O', 'error count'],
class_names=['not stable', 'stable'],
filled=True)
plt.show()
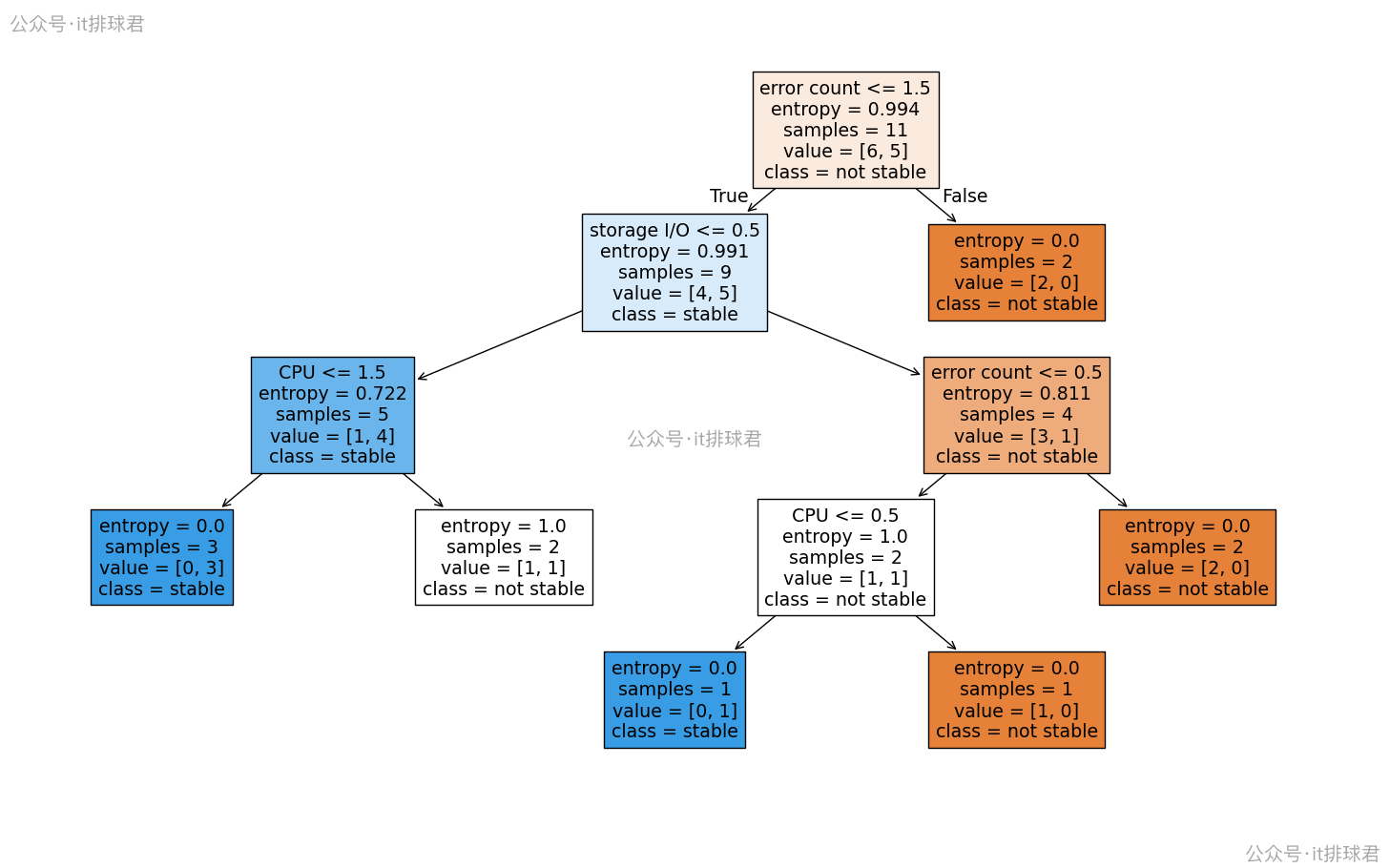
分析绘图
- 每个矩形框代表一个决策节点(叶子节点),比如第一个框,
error count<1.5表示用该特征来分类,1.5是基于输入的数据计算出来的,模型认为1.5是特征分割点 - entropy:当前节点的不确定性(越低越纯)
- samples:这个节点上的样本数
- value=[不稳定数, 稳定数]:类别分布
- class:当前节点最终被分类的类别
深入理解决策树
熵(entropy)
在图中有一个重要的指标,entropy。它是衡量数据纯度(不确定性)的指标,熵越低,表示类别越“纯”(不确定性越低);熵越高,代表数据越混杂
Entropy(D)=−∑i=1kpilog2pi Entropy(D) = - \sum_{i=1}^{k} p_i \log_2 p_i Entropy(D)=−i=1∑kpilog2pi
- D 是某个数据集(或某个节点上的样本)
- k 是类别数量(如“稳定”“不稳定”就是2类)
- pip_ipi 是第i类在该数据集中的比例
比如某节点:

样本数samples=5,类别value=[1,4]
p1=15,p2=45p_1=\frac{1}{5},p_2=\frac{4}{5}p1=51,p2=54
Entropy(D)=−(15⋅log215+45⋅log245)=0.7215Entropy(D) = - (\frac{1}{5}⋅log_2\frac{1}{5}+\frac{4}{5}⋅log_2\frac{4}{5}) = 0.7215Entropy(D)=−(51⋅log251+54⋅log254)=0.7215
熵越小,那就代表了该节点不确定性越低,如果该节点的上为0,那就不会继续分裂下去产生子节点;而不确定性越高的节点,就会继续分裂产生叶子节点
信息增益
是决策树中用于选择划分特征的核心指标。它本质上衡量的是:“使用某个特征进行划分后,数据的不确定性减少了多少”
信息增益=原始熵−加权熵
比如以下节点,想要计算出信息增益
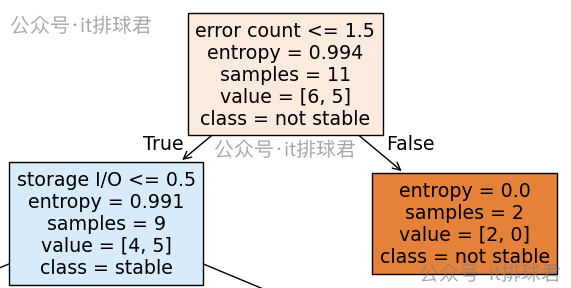
原始熵我们已经有了,那就是0.994,需要计算加权熵
加权熵=911⋅0.991+211⋅0=0.811加权熵=\frac{9}{11}⋅0.991+\frac{2}{11}⋅0=0.811加权熵=119⋅0.991+112⋅0=0.811
原始熵=0.994−0.811=0.183原始熵=0.994−0.811= 0.183原始熵=0.994−0.811=0.183
通过特征error count <= 1.5划分所带来的信息增益为0.183,也就是减少了 18.3% 的“混乱”程度
- 那该特征就是信息增益最大的特征了?
- 特征选的0.5、1.5的值是怎么来的?
特征选取的0.5、1.5从何而来
特征从“低”、“中”、“高”等文字描述转换成,0 1 2等数字,比如CPU可能的取值是[0,1,2],那就可以尝试划分出阈值中位点
(0+1)/2=0.5
(1+2)/2=1.5
所以在选取划分点的时候就会参考中位点进行划分
选取信息增益最大的特征
| 日志报错数 | 日志报错数数字化 | 系统是否稳定 |
|---|---|---|
| 少 | 0 | 稳定 |
| 少 | 0 | 稳定 |
| 少 | 0 | 稳定 |
| 多 | 2 | 不稳定 |
| 中 | 1 | 不稳定 |
| 少 | 0 | 不稳定 |
| 中 | 1 | 稳定 |
| 多 | 2 | 不稳定 |
| 少 | 0 | 不稳定 |
| 中 | 1 | 不稳定 |
| 少 | 0 | 稳定 |
先选择error count以1.5为划分点
error count<=1.5有9条,稳定与不稳定的比例为[5, 4]error count>1.5有2条,并且都是不稳定的
计算一下信息增益:
- 首先计算原始熵:11个样本中,5个稳定,6个不稳定,Entropy=−(611⋅log2611+511⋅log2511)≈0.994Entropy=-(\frac{6}{11}⋅log_2\frac{6}{11}+\frac{5}{11}⋅log_2\frac{5}{11}) \approx 0.994Entropy=−(116⋅log2116+115⋅log2115)≈0.994
- 再计算
error count>=1.5的熵:Entropy1=−(49⋅log249+59⋅log259)≈0.991Entropy_1=-(\frac{4}{9}⋅log_2\frac{4}{9}+\frac{5}{9}⋅log_2\frac{5}{9}) \approx 0.991Entropy1=−(94⋅log294+95⋅log295)≈0.991 - 再计算
error count>1.5的熵,由于全是不稳定,所以熵是0
- 再计算
- 计算加权熵:Entropyweighted=911⋅0.991+211⋅0≈0.811Entropy_{weighted}=\frac{9}{11}⋅0.991+\frac{2}{11}⋅0 \approx 0.811Entropyweighted=119⋅0.991+112⋅0≈0.811
- 信息增益:0.994-0.811=0.183
选择error count以0.5为划分点
error count<=0.5有6条,稳定与不稳定的比例为[4, 2]error count>0.5有5条,稳定与不稳定的比例为[1, 4]首先计算原始熵:上面已经计算过了,0.994
- 再计算
error count<=0.5的熵:Entropy1=−(46⋅log246+26⋅log226)≈0.918Entropy_1=-(\frac{4}{6}⋅log_2\frac{4}{6}+\frac{2}{6}⋅log_2\frac{2}{6}) \approx 0.918Entropy1=−(64⋅log264+62⋅log262)≈0.918 - 再计算
error count>0.5的熵:Entropy2=−(15⋅log215+45⋅log245)≈0.722Entropy_2=-(\frac{1}{5}⋅log_2\frac{1}{5}+\frac{4}{5}⋅log_2\frac{4}{5}) \approx 0.722Entropy2=−(51⋅log251+54⋅log254)≈0.722
- 再计算
计算加权熵:Entropyweighted=611⋅0.918+511⋅0.722≈0.829Entropy_{weighted}=\frac{6}{11}⋅0.918+\frac{5}{11}⋅0.722 \approx 0.829Entropyweighted=116⋅0.918+115⋅0.722≈0.829
信息增益:0.994-0.829=0.165
综上所述,error count为特征,以1.5为划分点,是合适的选择。并且将每个特征的每个划分点遍历一遍,得出error count<=1.5是熵下降最快的划分点

小结
算法步骤:
- 计算当前数据集的熵
- 对每个特征求出信息增益
- 选择信息增益最大的特征进行节点分类
- 重复以上步骤,直至熵为0,或者特征用完,或者数到达规定层数
有位彦祖说到,这不就是ID3算法嘛,基于信息熵作为划分标准。其实说对了一部分,文中使用的代码
clf = DecisionTreeClassifier(criterion='entropy', random_state=0)
criterion='entropy'使用的是的算法是整合了CART算法+ID3的信息熵分类等多种算法思想融合而来
基尼指数
之前讨论了通过熵的方式来划分节点,本节讨论基尼指数来划分节点
Gini(S)=1−∑i=1npi2 Gini(S) = 1 - \sum_{i=1}^{n} p_i^2 Gini(S)=1−i=1∑npi2
- n:数据集中类别的数量
- pip_ipi:数据集中第 iii 类的概率
clf = DecisionTreeClassifier(criterion='gini', random_state=0)
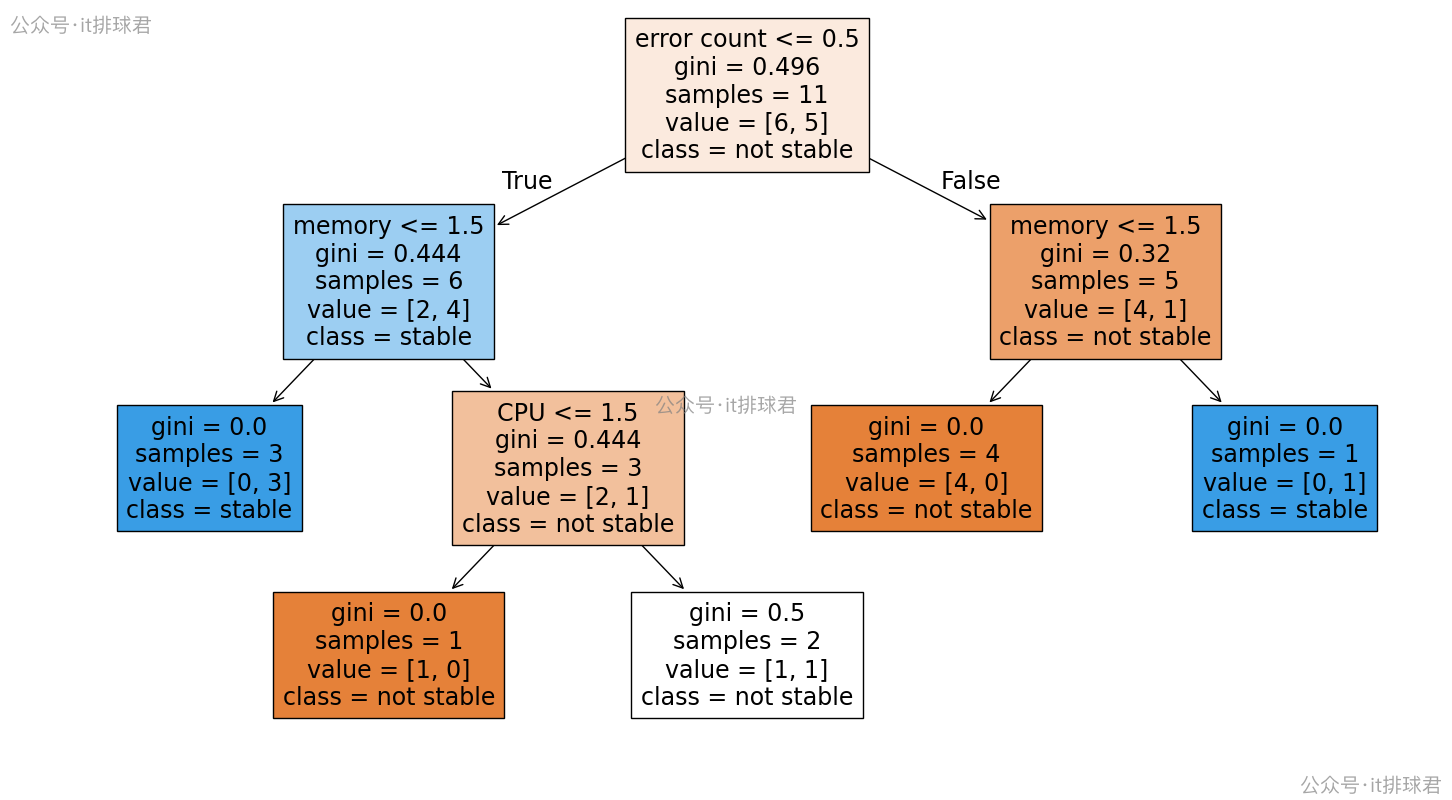
使用基尼指数,选择了error count<=0.5作为划分特征,与熵不一样
基尼增益
选择error count<=0.5
error count<=0.5有6条,稳定与不稳定的比例为[4, 2]error count>0.5有5条,稳定与不稳定的比例为[1, 4]
计算一下基尼增益:
- 原始基尼指数:Gini=1−∑i=1npi2=1−((511)2−(611)2≈0.496)Gini = 1 - \sum_{i=1}^{n} p_i^2 = 1-((\frac{5}{11})^2-(\frac{6}{11})^2 \approx 0.496)Gini=1−∑i=1npi2=1−((115)2−(116)2≈0.496)
- 计算
error count<=0.5的基尼指数,Gini1=1−((46)2+(26)2)≈0.4445Gini_1=1-((\frac{4}{6})^2+(\frac{2}{6})^2) \approx 0.4445Gini1=1−((64)2+(62)2)≈0.4445 - 计算
error count>0.5的基尼指数,Gini2=1−((15)2+(45)2)=0.32Gini_2=1-((\frac{1}{5})^2+(\frac{4}{5})^2) = 0.32Gini2=1−((51)2+(54)2)=0.32
- 计算
- 计算加权平均基尼指数:Giniweighted=611⋅0.4445+511⋅0.32≈0.3870Gini_{weighted}=\frac{6}{11}⋅0.4445 + \frac{5}{11}⋅0.32 \approx 0.3870Giniweighted=116⋅0.4445+115⋅0.32≈0.3870
- 基尼增益:0.4959 - 0.3870=0.1089
选择error count<=1.5
error count<=1.5有9条,稳定与不稳定的比例为[5, 4]error count>1.5有2条,并且都是不稳定的
计算一下基尼增益:
- 原始基尼指数:上面已经计算过,0.0496
- 计算
error count<=1.5的基尼指数,Gini1=1−((59)2+(49)2)≈0.4939Gini_1=1-((\frac{5}{9})^2+(\frac{4}{9})^2) \approx 0.4939Gini1=1−((95)2+(94)2)≈0.4939 - 计算
error count>1.5的基尼指数,由于全是不稳定,Gini2=1−((02)2+(22)2)=0Gini_2=1-((\frac{0}{2})^2+(\frac{2}{2})^2) = 0Gini2=1−((20)2+(22)2)=0
- 计算
- 计算加权平均基尼指数:Giniweighted=911⋅0.4939≈0.4041Gini_{weighted}=\frac{9}{11}⋅0.4939 \approx 0.4041Giniweighted=119⋅0.4939≈0.4041
- 基尼增益:0.4959 - 0.4041=0.0918
小结
综上所述,error count为特征,以0.5为划分点,是合适的选择
使用基尼指数,选择特征划分点的时候,与熵的行为完全不一样,下面列一下基尼指数与熵的对比
| 基尼指数 | 熵 | |
|---|---|---|
| 参数 | criterion=‘gini’ | criterion=‘entropy’ |
| 划分标准 | 基尼指数(Gini Index) | 信息增益(Information Gain) |
| 计算效率 | 更高(无对数运算) | 较低(需计算对数) |
| 分裂倾向 | 偏向生成平衡的树 | 可能生成更深的树 |
| 类别 | 对类别分布变化更敏感(如某一类别占比从40%→50%时,基尼指数变化更明显) | 对极端概率更敏感(如某一类别占比接近0%或100%时,熵变化剧烈) |
| sklearn | 默认使用 | 需指定criterion=‘entropy’ |
剪枝
所谓剪枝,是提高决策树泛化能力的一种策略,剪枝的核心思想是减少数的复杂度,决策树通过找到最大的信息增益,不断迭代的划分节点分类,不断的迭代划分,就会造成树的复杂度不断提高
预剪枝
预剪枝:在构建决策树的过程中就进行限制,提前停止树的生长
- 设置最大深度,
max_depth - 设置叶子节点最小样本数,
min_samples_leaf - 设置内部节点最小样本数,
min_samples_split - 设置信息增益阈值(如增益低于某一阈值就不分裂)
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_predict, StratifiedKFold
from sklearn.metrics import classification_report
X, y = load_iris(return_X_y=True)
cv = StratifiedKFold(n_splits=5, shuffle=True)
model = DecisionTreeClassifier(max_depth=3, min_samples_leaf=3, random_state=0)
y_pred = cross_val_predict(model, X, y, cv=cv)
print("预剪枝 分类报告:\n")
print(classification_report(y, y_pred, zero_division=0))
后剪枝
后剪枝:先让树尽可能长大(完全生长),然后再自底向上地修剪枝叶。sklearn中默认采用:成本复杂度剪枝(Cost Complexity Pruning,也叫 α-剪枝):用代价函数考虑准确率与模型复杂度的权衡
from sklearn.model_selection import cross_val_score
import numpy as np
model = DecisionTreeClassifier(random_state=0)
path = model.cost_complexity_pruning_path(X, y)
ccp_alphas = path.ccp_alphas[:-1]
mean_scores = []
for alpha in ccp_alphas:
clf = DecisionTreeClassifier(random_state=0, ccp_alpha=alpha)
scores = cross_val_score(clf, X, y, cv=5, scoring='accuracy')
mean_scores.append(scores.mean())
best_alpha = ccp_alphas[np.argmax(mean_scores)]
print("最佳 ccp_alpha:", best_alpha)
best_model = DecisionTreeClassifier(random_state=0, ccp_alpha=best_alpha)
best_model.fit(X, y)
y_pred = best_model.predict(X)
print("后剪枝 分类报告:")
print(classification_report(y, y_pred))
- 首先训练处一颗完整树
- 从底部开始,找到最小的子树节点t,将其子树 TtT_tTt 剪成一个叶子节点
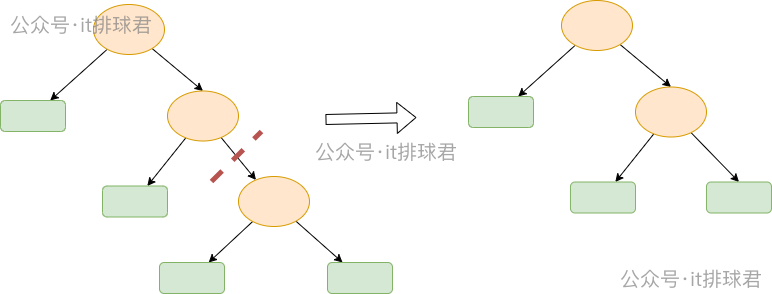
- 计算剪枝后误差的变化,得到αt\alpha_tαt
- 其中损失函数可以使用多种方式计算,由于sklearn默认使用的是基尼指数,那就用基尼指数来计算误差α=R(t)−R(Tt)∣Tt∣−1\alpha = \frac{R(t)-R(T_t)}{|T_t|-1}α=∣Tt∣−1R(t)−R(Tt)
- R(t)R(t)R(t):父节点的基尼指数
- R(Tt)R(T_t)R(Tt):剪枝前加权基尼指数
- ∣Tt∣|T_t|∣Tt∣:叶节点数
- 其中损失函数可以使用多种方式计算,由于sklearn默认使用的是基尼指数,那就用基尼指数来计算误差α=R(t)−R(Tt)∣Tt∣−1\alpha = \frac{R(t)-R(T_t)}{|T_t|-1}α=∣Tt∣−1R(t)−R(Tt)
- 上一步拿到的α\alphaα,与
ccp_alpha超参数(提前设置)进行对比,如果ccp_alpha>α\alphaα,则减掉该子树 - 重复以上过程
举一个例子,来看下该节点(CPU<=1.5)是否应该被剪枝
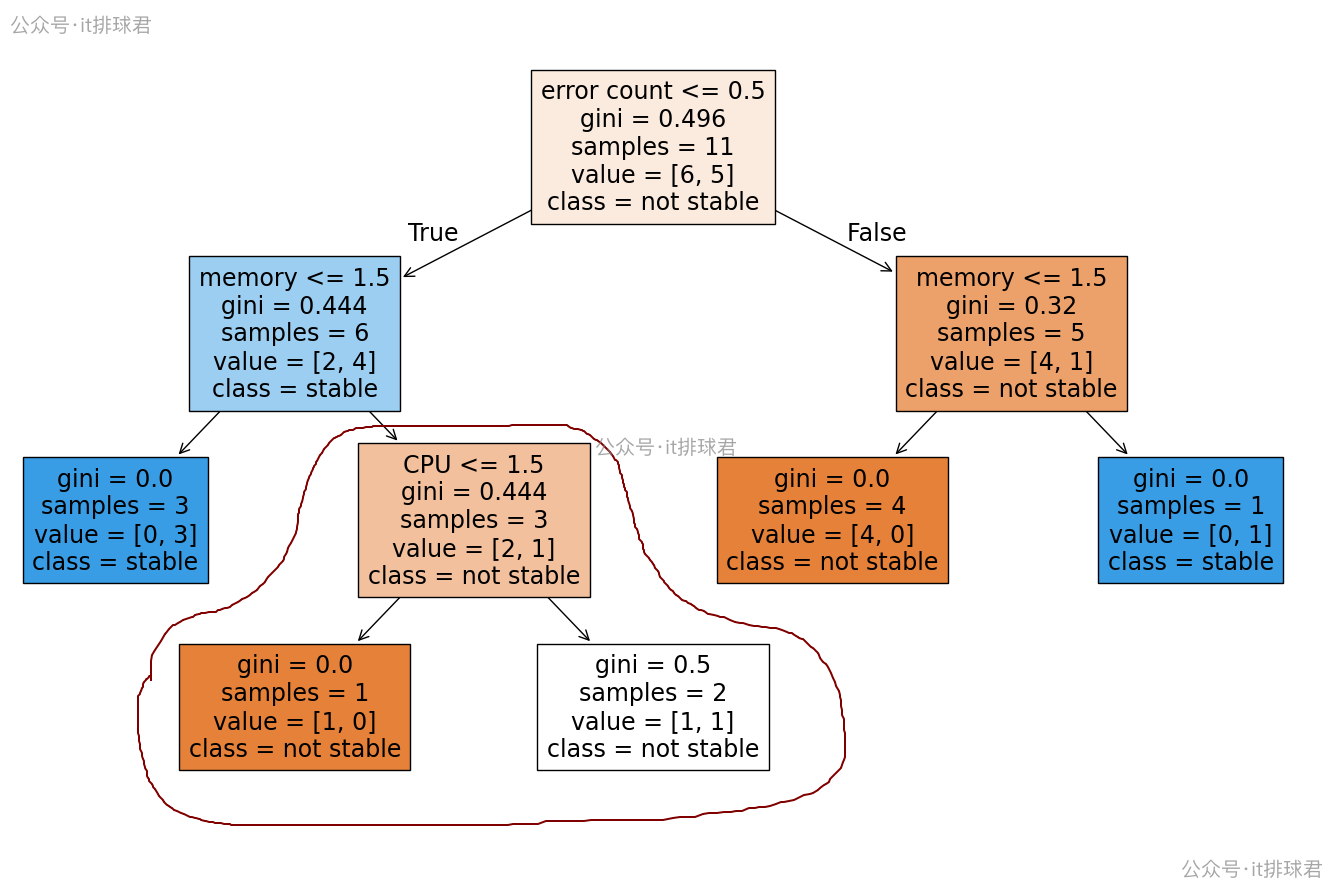
- 父节点的基尼指数:R(t)=0.444R(t)=0.444R(t)=0.444
- 加权平均基尼指数:
- 父节点的加权基尼指数:36⋅0.444=0.222\frac{3}{6}⋅0.444=0.22263⋅0.444=0.222
- 左子树的加权基尼指数:16⋅0\frac{1}{6}⋅061⋅0
- 右子树的加权基尼指数:26⋅0.5≈0.166\frac{2}{6}⋅0.5 \approx 0.16662⋅0.5≈0.166
- 子树的加权基尼指数:0.222+0+0.166=0.3880.222+0+0.166=0.3880.222+0+0.166=0.388
- α=0.444−0.1663−1=0.028\alpha = \frac{0.444-0.166}{3-1}=0.028α=3−10.444−0.166=0.028
如果超参数ccp_alpha>0.028,那该节点就将剪枝
联系我
- 联系我,做深入的交流

至此,本文结束
在下才疏学浅,有撒汤漏水的,请各位不吝赐教…