题目描述
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例
示例 1:
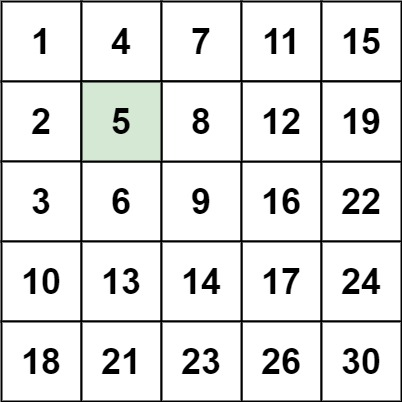
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true
示例 2:
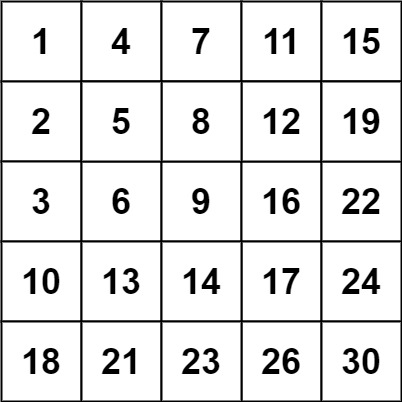
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出:false
解法
1.暴力
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(),n = matrix[0].size();
for(int i = 0;i < m;i ++){
for(int j = 0;j < n;j ++){
if(matrix[i][j] == target) return true;
else if(matrix[i][j] > target) break;
if(matrix[i][j] > target && j == n - 1) return false;
}
}
return false;
}
};算法思路
利用矩阵每行都是递增的这一特性,设计一个二层循环,逐行搜索。
时间复杂度:O(NM),空间复杂度:O(1)
2.贪心
解题思路:
若使用暴力法遍历矩阵 matrix ,则时间复杂度为 O(NM) 。暴力法未利用矩阵 “从上到下递增、从左到右递增” 的特点,显然不是最优解法。
如下图所示,我们将矩阵逆时针旋转 45° ,并将其转化为图形式,发现其类似于 二叉搜索树 ,即对于每个元素,其左分支元素更小、右分支元素更大。因此,通过从 “根节点” 开始搜索,遇到比 target 大的元素就向左,反之向右,即可找到目标值 target 。
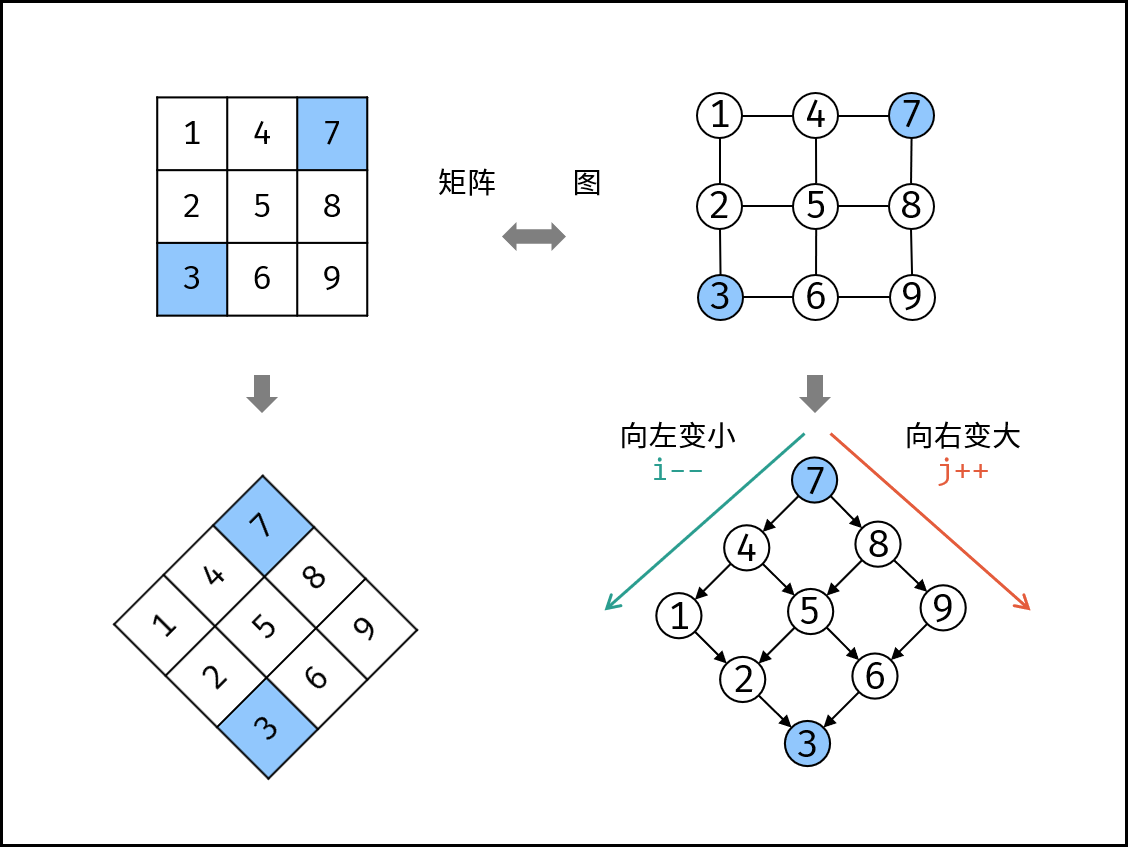
“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素,本文称之为 标志数 ,以 matrix 中的 左下角元素 为标志数 flag ,则有:
若 flag > target ,则 target 一定在 flag 所在 行的上方 ,即 flag 所在行可被消去。
若 flag < target ,则 target 一定在 flag 所在 列的右方 ,即 flag 所在列可被消去。
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int i = matrix.size() - 1, j = 0;
while(i >= 0 && j < matrix[0].size())
{
if(matrix[i][j] > target) i--;
else if(matrix[i][j] < target) j++;
else return true;
}
return false;
}
};
算法流程
1.从矩阵 matrix 左下角元素(索引设为 (i, j) )开始遍历,并与目标值对比:
· 当 matrix[i][j] > target 时,执行 i-- ,即消去第 i 行元素。
· 当 matrix[i][j] < target 时,执行 j++ ,即消去第 j 列元素。
· 当 matrix[i][j] = target 时,返回 true ,代表找到目标值。
2.若行索引或列索引越界,则代表矩阵中无目标值,返回 false 。
时间复杂度:O(M+N),空间复杂度:O(1)