From sztu 自动化专业的小菜鸡。
时间序列预测问题是一种困难类型的预测建模问题。
与回归预测建模不同,时间序列还增加了输入变量之间序列依赖性的复杂性。
一种用于处理序列依赖性的强大神经网络称为 循环神经网络 。 长短期记忆网络或 LSTM 网络是一种用于深度学习的循环神经网络,因为可以成功训练非常大的架构。
在这篇文章中,您将了解如何使用 Keras 深度学习库在 Python 中开发 LSTM 网络,以解决演示时间序列预测问题。
完成本教程后,您将了解如何为您自己的时间序列预测问题和其他更一般的序列问题实现和开发 LSTM 网络。 你会知道:
- 关于国际航空公司乘客时间序列预测问题。
- 如何为基于回归、窗口和时间步长的时间序列预测问题框架开发 LSTM 网络。
- 如何使用在很长的序列中保持状态(记忆)的 LSTM 网络进行开发和预测。
在本教程中,我们将为标准时间序列预测问题开发许多 LSTM。 LSTM 网络的问题和选择的配置仅用于演示目的,它们没有进行优化。
这些示例将准确地向您展示如何为时间序列预测建模问题开发自己的不同结构的 LSTM 网络。
获取数据集,这儿可以使用您想做lstm预测的数据集。
import pandas
import matplotlib.pyplot as plt
dataset = pandas.read_csv('airline-passengers.csv', usecols=[1], engine='python')
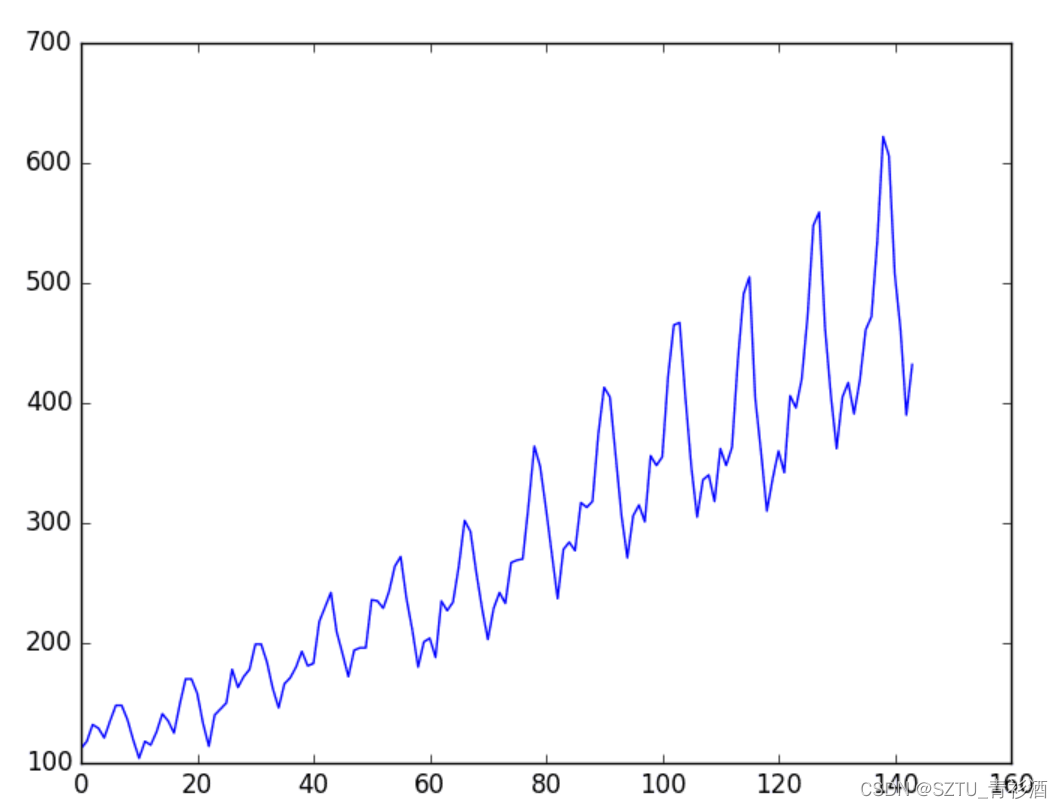
plt.plot(dataset)
plt.show()随着时间的推移,您可以看到数据集中的上升趋势。
您还可以看到可能对应于北半球假期的数据集的一些周期性。
我们将保持简单并按原样处理数据。
通常,研究各种数据准备技术以重新调整数据并使其静止是一个好主意。
长短期记忆网络
Long Short-Term Memory 网络或 LSTM 网络是一种循环神经网络,它使用随时间的反向传播进行训练,并克服了梯度消失问题。
因此,它可用于创建大型循环网络,进而可用于解决机器学习中的困难序列问题并获得最先进的结果。
LSTM 网络没有神经元,而是具有通过层连接的内存块。
块具有使其比经典神经元更智能的组件和最近序列的记忆。 块包含管理块状态和输出的门。 块对输入序列进行操作,块内的每个门都使用 sigmoid 激活单元来控制它们是否被触发,从而使状态的改变和流经块的信息的添加成为有条件的。
一个单元内有三种类型的门:
- 忘记门 :有条件地决定从块中丢弃哪些信息。
- 输入门 :有条件地决定输入中的哪些值来更新内存状态。
- 输出门 :根据输入和块的内存有条件地决定输出什么。
每个单元就像一个迷你状态机,其中单元的门具有在训练过程中学习的权重。
您可以看到如何从 LSTM 层实现复杂的学习和记忆,并且不难想象高阶抽象如何与多个这样的层分层。
用于回归的 LSTM 网络
我们可以将问题表述为回归问题。
也就是说,给定本月的乘客数量(以千为单位),下个月的乘客数量是多少?
我们可以编写一个简单的函数将我们的单列数据转换为两列数据集:第一列包含本月 (t) 的乘客人数,第二列包含下个月 (t+1) 的乘客人数,以进行预测。
在开始之前,让我们首先导入我们打算使用的所有函数和类。 这假设安装了 Keras 深度学习库的工作 SciPy 环境。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error在我们做任何事情之前,最好先修复随机数种子,以确保我们的结果是可重现的。
# fix random seed for reproducibility
tf.random.set_seed(7)我们还可以使用上一节中的代码将数据集加载为 Pandas 数据框。 然后我们可以从数据帧中提取 NumPy 数组并将整数值转换为浮点值,这更适合使用神经网络进行建模。
# load the dataset
dataframe = pd.read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')LSTM 对输入数据的规模很敏感,特别是在使用 sigmoid(默认)或 tanh 激活函数时。 将数据重新缩放到 0 到 1 的范围是一个很好的做法,也称为规范化。 我们可以使用 MinMaxScaler scikit-learn 库
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)在我们对数据进行建模并估计模型在训练数据集上的技能之后,我们需要了解模型在新的看不见的数据上的技能。 对于正常的分类或回归问题,我们将使用交叉验证来完成。
对于时间序列数据,值的顺序很重要。 我们可以使用的一种简单方法是将有序数据集拆分为训练数据集和测试数据集。 下面的代码计算分割点的索引,并将数据分成训练数据集,其中 67% 的观察可以用来训练我们的模型,剩下的 33% 用于测试模型。
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
print(len(train), len(test))现在我们可以定义一个函数来创建一个新的数据集,如上所述。
该函数有两个参数: dataset ,它是我们想要转换为数据集的 NumPy 数组,以及 look_back ,它是用作预测下一个时间段的输入变量的先前时间步数 - 在这种情况下默认为 1。
此默认设置将创建一个数据集,其中 X 是给定时间 (t) 的乘客数量,Y 是下一次 (t + 1) 的乘客数量。
它可以配置,我们将在下一节中构建一个不同形状的数据集。
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return np.array(dataX), np.array(dataY)让我们看一下这个函数对数据集第一行的影响(为了清楚起见,以非规范化的形式显示)。
X Y
112 118
118 132
132 129
129 121
121 135如果将前 5 行与上一节中列出的原始数据集样本进行比较,您可以在数字中看到 X=t 和 Y=t+1 模式。
让我们使用这个函数来准备训练和测试数据集以进行建模。
# reshape into X=t and Y=t+1
look_back = 1
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)LSTM 网络期望输入数据 (X) 以以下形式提供特定的数组结构: [样本、时间步长、特征] 。
目前,我们的数据采用以下形式:[ samples, features ],我们将问题构建为每个样本的一个时间步长。 将准备好的训练和测试输入数据转换为预期的结构 numpy.reshape() ,如下所示:
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = np.reshape(testX, (testX.shape[0], 1, testX.shape[1]))我们现在准备好为这个问题设计和拟合我们的 LSTM 网络。
该网络有一个带有 1 个输入的可见层,一个带有 4 个 LSTM 块或神经元的隐藏层,以及一个进行单值预测的输出层。 默认的 sigmoid 激活函数用于 LSTM 块。 网络训练了 100 个 epoch,使用了 1 的批大小。
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(1, look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)一旦模型拟合好,我们就可以估计模型在训练和测试数据集上的性能。 这将为我们提供新模型的比较点。
请注意,我们在计算错误分数之前反转预测,以确保以与原始数据相同的单位(每月数千名乘客)报告性能。
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = np.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = np.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))最后,我们可以使用模型为训练和测试数据集生成预测,以获得模型技能的视觉指示。
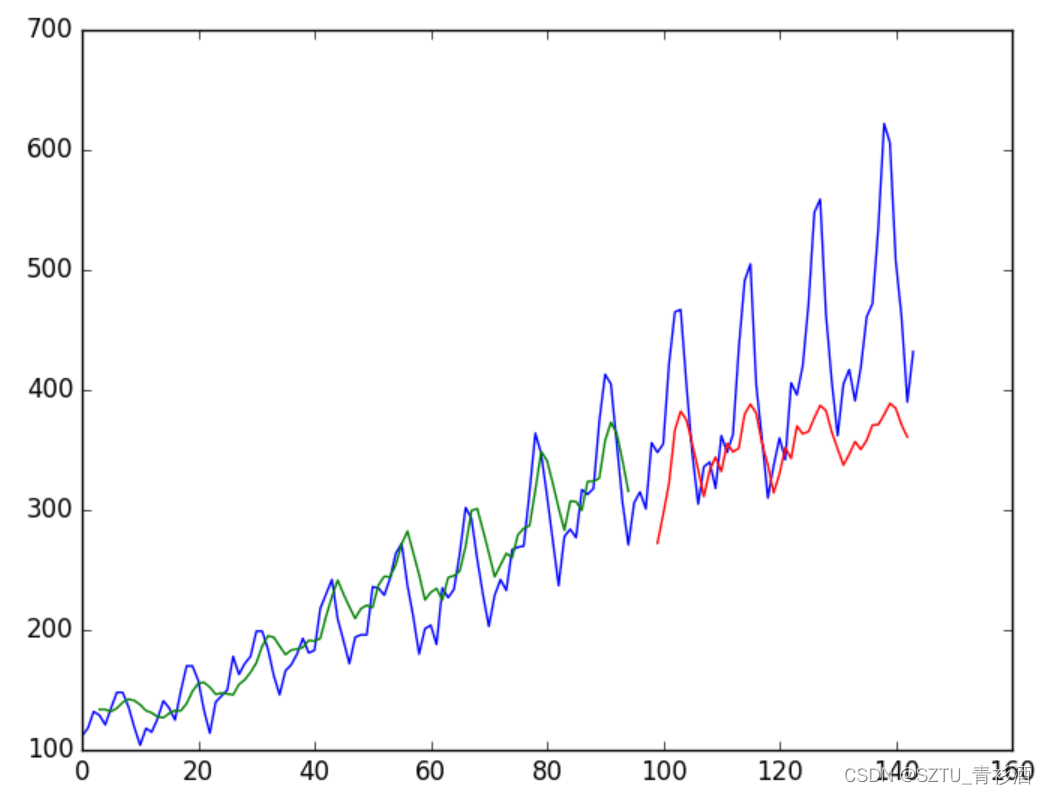
由于数据集的准备方式,我们必须改变预测,使它们在 x 轴上与原始数据集对齐。 准备好后,将绘制数据,以蓝色显示原始数据集,以绿色显示训练数据集的预测,以红色显示未见过的测试数据集的预测。
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()我们可以看到该模型在拟合训练和测试数据集方面做得非常出色。
为了完整起见,下面是整个代码示例。
# LSTM for international airline passengers problem with regression framing
import numpy as np
import matplotlib.pyplot as plt
from pandas import read_csv
import math
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return np.array(dataX), np.array(dataY)
# fix random seed for reproducibility
tf.random.set_seed(7)
# load the dataset
dataframe = read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 1
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = np.reshape(testX, (testX.shape[0], 1, testX.shape[1]))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(1, look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = np.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = np.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()注意 :您的 结果可能会因 算法或评估程序的随机性或数值精度的差异而有所不同。 考虑运行该示例几次并比较平均结果。
运行该示例会产生以下输出。
...
Epoch 95/100
94/94 - 0s - loss: 0.0021 - 37ms/epoch - 391us/step
Epoch 96/100
94/94 - 0s - loss: 0.0020 - 37ms/epoch - 398us/step
Epoch 97/100
94/94 - 0s - loss: 0.0020 - 37ms/epoch - 396us/step
Epoch 98/100
94/94 - 0s - loss: 0.0020 - 37ms/epoch - 391us/step
Epoch 99/100
94/94 - 0s - loss: 0.0020 - 37ms/epoch - 394us/step
Epoch 100/100
94/94 - 0s - loss: 0.0020 - 36ms/epoch - 382us/step
3/3 [==============================] - 0s 490us/step
2/2 [==============================] - 0s 461us/step
Train Score: 22.68 RMSE
Test Score: 49.34 RMSE我们可以看到,该模型在训练数据集上的平均误差约为 23 名乘客(以千计),在测试数据集上的平均误差约为 49 名乘客(以千计)。 没有那么糟糕。
使用窗口方法进行回归的 LSTM
我们还可以对问题进行表述,以便可以使用多个最近的时间步来预测下一个时间步。
这称为窗口,窗口的大小是可以针对每个问题进行调整的参数。
例如,给定当前时间 (t),我们想要预测序列 (t+1) 中下一个时间的值,我们可以使用当前时间 (t) 以及之前的两个时间 (t-1和 t-2) 作为输入变量。
当表述为回归问题时,输入变量为 t-2、t-1、t,输出变量为 t+1。
的 create_dataset() 函数允许我们通过将 look_back 参数从 1 增加到 3 来创建时间序列问题的这个公式。
具有此公式的数据集示例如下所示:
X1 X2 X3 Y
112 118 132 129
118 132 129 121
132 129 121 135
129 121 135 148
121 135 148 148我们可以使用更大的窗口大小重新运行上一节中的示例。 为了完整起见,下面列出了仅更改窗口大小的整个代码清单。
# LSTM for international airline passengers problem with window regression framing
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from pandas import read_csv
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return np.array(dataX), np.array(dataY)
# fix random seed for reproducibility
tf.random.set_seed(7)
# load the dataset
dataframe = read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = np.reshape(testX, (testX.shape[0], 1, testX.shape[1]))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(1, look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = np.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = np.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()注意 :您的 结果可能会因 算法或评估程序的随机性或数值精度的差异而有所不同。 考虑运行该示例几次并比较平均结果。
运行示例提供以下输出:
Epoch 95/100
92/92 - 0s - loss: 0.0023 - 35ms/epoch - 384us/step
Epoch 96/100
92/92 - 0s - loss: 0.0023 - 36ms/epoch - 389us/step
Epoch 97/100
92/92 - 0s - loss: 0.0024 - 37ms/epoch - 404us/step
Epoch 98/100
92/92 - 0s - loss: 0.0023 - 36ms/epoch - 392us/step
Epoch 99/100
92/92 - 0s - loss: 0.0022 - 36ms/epoch - 389us/step
Epoch 100/100
92/92 - 0s - loss: 0.0022 - 35ms/epoch - 384us/step
3/3 [==============================] - 0s 514us/step
2/2 [==============================] - 0s 533us/step
Train Score: 24.86 RMSE
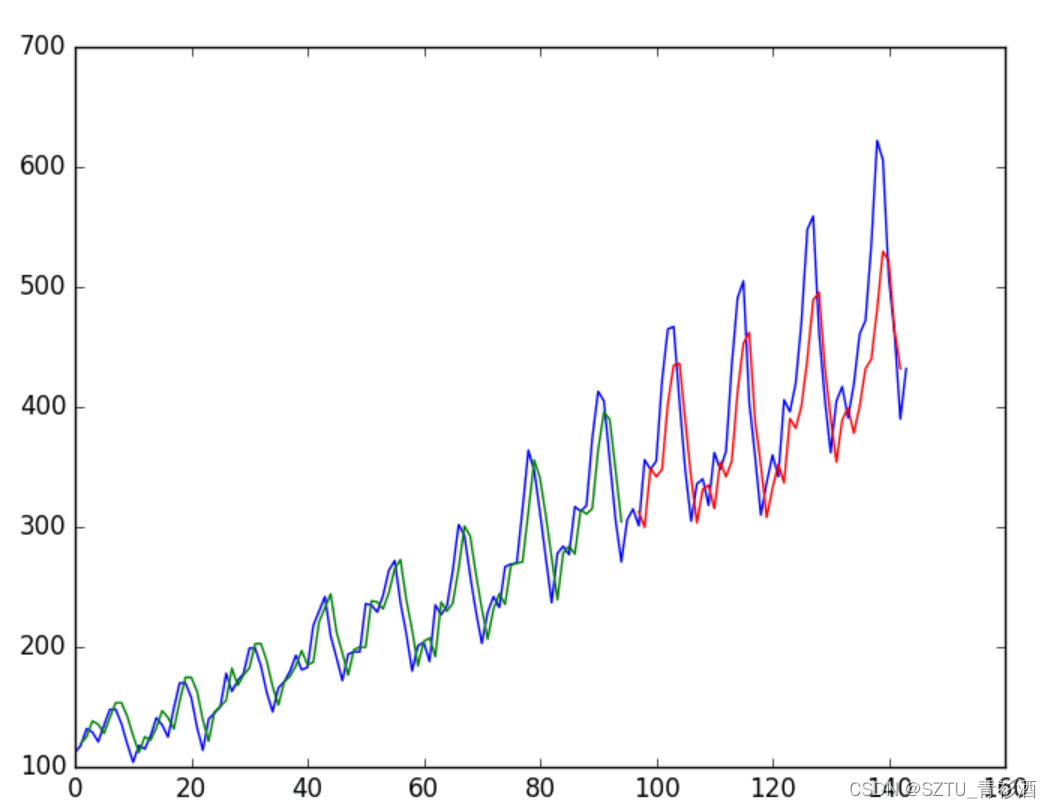
Test Score: 70.48 RMSE我们可以看到,与上一节相比,误差略有增加。 未调整窗口大小和网络架构:这只是演示如何构建预测问题。
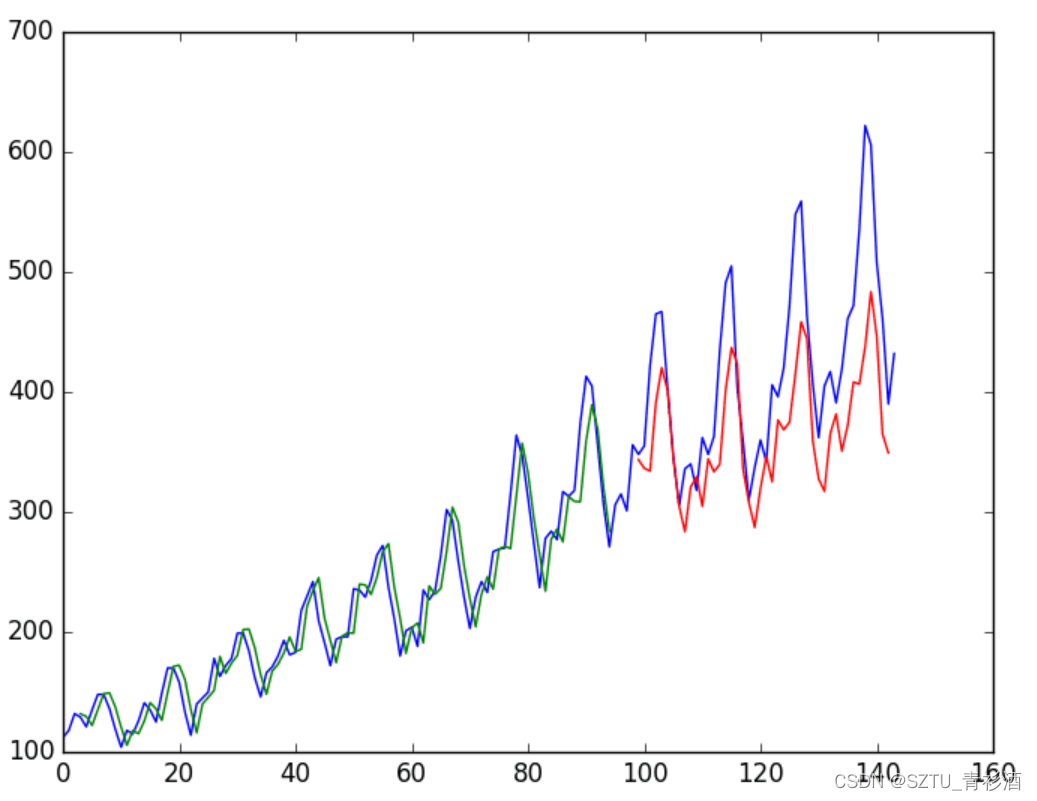
用于时间步长回归的 LSTM
您可能已经注意到 LSTM 网络的数据准备包括时间步长。
一些序列问题的每个样本可能有不同数量的时间步长。 例如,您可能对导致故障点或浪涌点的物理机器进行测量。 每个事件都是一个样本,导致事件的观察结果是时间步长,观察到的变量是特征。
时间步长提供了另一种表述时间序列问题的方法。 就像上面的窗口示例一样,我们可以将时间序列中的先前时间步长作为输入来预测下一个时间步长的输出。
我们可以将过去的观察作为单独的输入特征,而不是将它们作为一个输入特征的时间步长,这确实是对问题的更准确的框架。
我们可以使用与前面基于窗口的示例相同的数据表示来做到这一点,除了当我们重塑数据时,我们将列设置为时间步长维度并将特征维度更改回 1。例如:
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0], testX.shape[1], 1))为了完整起见,下面提供了整个代码清单。
# LSTM for international airline passengers problem with time step regression framing
import numpy as np
import matplotlib.pyplot as plt
from pandas import read_csv
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return np.array(dataX), np.array(dataY)
# fix random seed for reproducibility
tf.random.set_seed(7)
# load the dataset
dataframe = read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0], testX.shape[1], 1))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(look_back, 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = np.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = np.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()注意 :您的 结果可能会因 算法或评估程序的随机性或数值精度的差异而有所不同。 考虑运行该示例几次并比较平均结果。
运行示例提供以下输出:
...
Epoch 95/100
92/92 - 0s - loss: 0.0023 - 45ms/epoch - 484us/step
Epoch 96/100
92/92 - 0s - loss: 0.0023 - 45ms/epoch - 486us/step
Epoch 97/100
92/92 - 0s - loss: 0.0024 - 44ms/epoch - 479us/step
Epoch 98/100
92/92 - 0s - loss: 0.0022 - 45ms/epoch - 489us/step
Epoch 99/100
92/92 - 0s - loss: 0.0022 - 45ms/epoch - 485us/step
Epoch 100/100
92/92 - 0s - loss: 0.0021 - 45ms/epoch - 490us/step
3/3 [==============================] - 0s 635us/step
2/2 [==============================] - 0s 616us/step
Train Score: 24.84 RMSE
Test Score: 60.98 RMSE我们可以看到结果比前面的例子稍微好一些,尽管输入数据的结构更有意义。
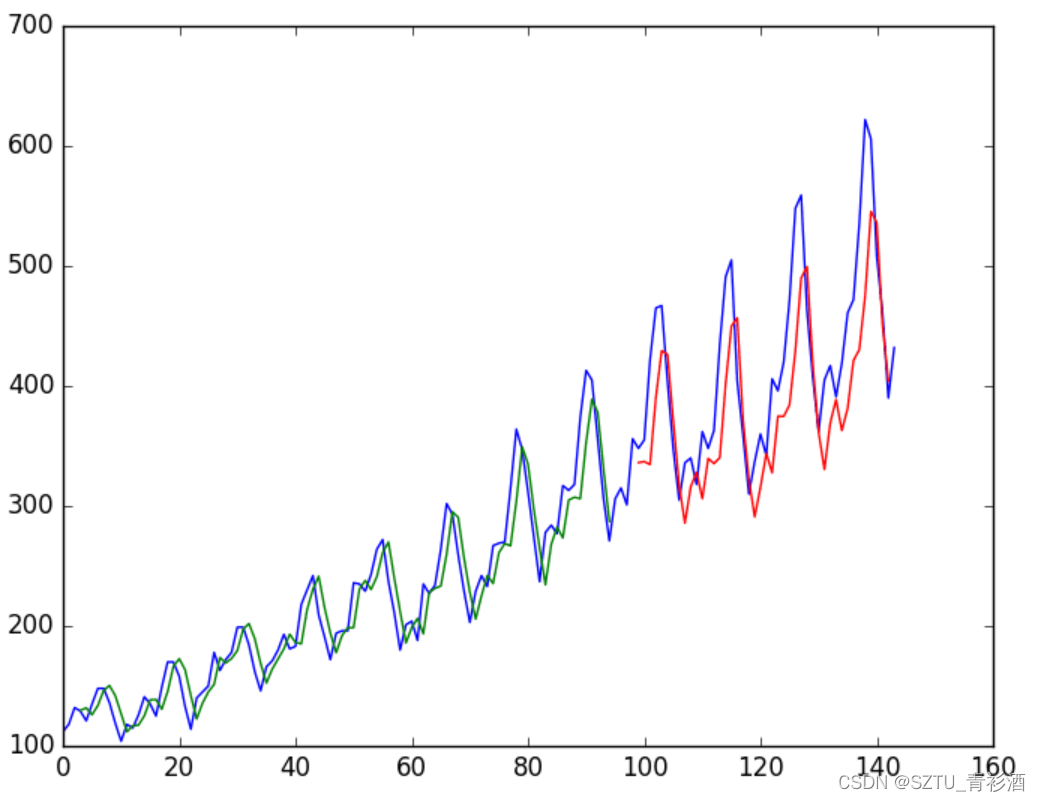
具有批次间记忆的 LSTM
LSTM 网络具有记忆,能够跨长序列记忆。
通常,在拟合模型时,网络中的状态会在每个训练批次后重置,以及每次调用 model.predict() 或 model.evaluate() 。
通过使 LSTM 层“有状态”,我们可以更好地控制何时在 Keras 中清除 LSTM 网络的内部状态。 这意味着它可以在整个训练序列上建立状态,甚至在需要进行预测时保持该状态。
它要求在拟合网络时不打乱训练数据。 它还需要在每次暴露于训练数据(epoch)后通过调用 model.reset_states() 。 这意味着我们必须创建自己的 epoch 外循环,并在每个 epoch 中调用 model.fit() 和 model.reset_states() 。 例如:
for i in range(100):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
model.reset_states()最后,当构建 LSTM 层时, 有状态 必须将 True ,而不是指定输入维度,我们必须硬编码批次中的样本数、样本中的时间步数和一次特征数一步一步设置 batch_input_shape 参数。 例如:
model.add(LSTM(4, batch_input_shape=(batch_size, time_steps, features), stateful=True))然后在评估模型和进行预测时必须使用相同的批量大小。 例如:
model.predict(trainX, batch_size=batch_size)我们可以调整前面的时间步示例以使用有状态的 LSTM。 下面提供了完整的代码清单。
# LSTM for international airline passengers problem with memory
import numpy as np
import matplotlib.pyplot as plt
from pandas import read_csv
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return np.array(dataX), np.array(dataY)
# fix random seed for reproducibility
tf.random.set_seed(7)
# load the dataset
dataframe = read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0], testX.shape[1], 1))
# create and fit the LSTM network
batch_size = 1
model = Sequential()
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
for i in range(100):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
model.reset_states()
# make predictions
trainPredict = model.predict(trainX, batch_size=batch_size)
model.reset_states()
testPredict = model.predict(testX, batch_size=batch_size)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = np.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = np.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()注意 :您的 结果可能会因 算法或评估程序的随机性或数值精度的差异而有所不同。 考虑运行该示例几次并比较平均结果。
运行示例提供以下输出:
...
92/92 - 0s - loss: 0.0024 - 46ms/epoch - 502us/step
92/92 - 0s - loss: 0.0023 - 49ms/epoch - 538us/step
92/92 - 0s - loss: 0.0023 - 47ms/epoch - 514us/step
92/92 - 0s - loss: 0.0023 - 48ms/epoch - 526us/step
92/92 - 0s - loss: 0.0022 - 48ms/epoch - 517us/step
92/92 - 0s - loss: 0.0022 - 48ms/epoch - 521us/step
92/92 - 0s - loss: 0.0022 - 47ms/epoch - 512us/step
92/92 - 0s - loss: 0.0021 - 50ms/epoch - 540us/step
92/92 - 0s - loss: 0.0021 - 47ms/epoch - 512us/step
92/92 - 0s - loss: 0.0021 - 52ms/epoch - 565us/step
92/92 [==============================] - 0s 448us/step
44/44 [==============================] - 0s 383us/step
Train Score: 24.48 RMSE
Test Score: 49.55 RMSE我们确实看到结果比一些好,比另一些差。 该模型可能需要更多模块,并且可能需要针对更多时期进行训练以内化问题的结构。
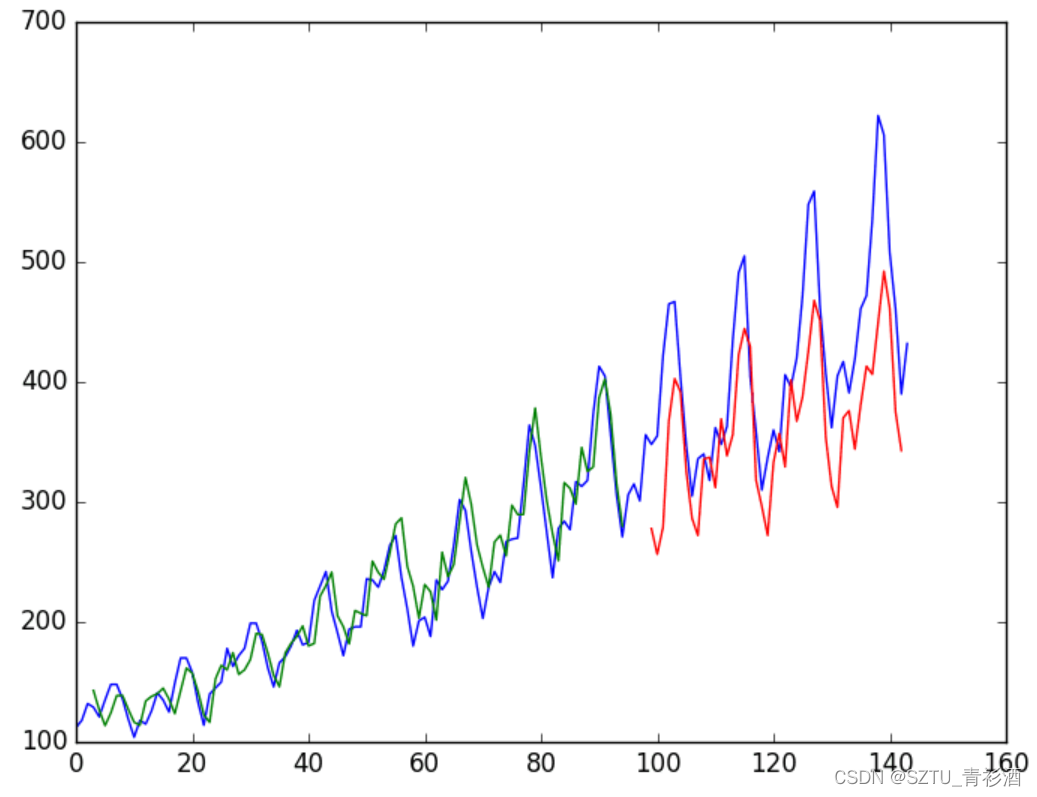
具有批次间内存的堆叠 LSTM
最后,我们将看看 LSTM 的一大优势:当它们堆叠到深度网络架构中时,它们可以被成功训练。
LSTM 网络可以在 Keras 中堆叠,就像其他层类型可以堆叠一样。 所需配置的一个补充是每个后续 LSTM 层之前的 LSTM 层必须返回序列。 这可以通过将图层上的 return_sequences 参数设置为 True 。
我们可以将上一节中的有状态 LSTM 扩展为具有两层,如下所示:
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True, return_sequences=True))
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))为了完整起见,下面提供了整个代码清单。
# Stacked LSTM for international airline passengers problem with memory
import numpy as np
import matplotlib.pyplot as plt
from pandas import read_csv
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return np.array(dataX), np.array(dataY)
# fix random seed for reproducibility
tf.random.set_seed(7)
# load the dataset
dataframe = read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0], testX.shape[1], 1))
# create and fit the LSTM network
batch_size = 1
model = Sequential()
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True, return_sequences=True))
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
for i in range(100):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
model.reset_states()
# make predictions
trainPredict = model.predict(trainX, batch_size=batch_size)
model.reset_states()
testPredict = model.predict(testX, batch_size=batch_size)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = np.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = np.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()注意 :您的 结果可能会因 算法或评估程序的随机性或数值精度的差异而有所不同。 考虑运行该示例几次并比较平均结果。
运行该示例会产生以下输出。
...
92/92 - 0s - loss: 0.0016 - 78ms/epoch - 849us/step
92/92 - 0s - loss: 0.0015 - 80ms/epoch - 874us/step
92/92 - 0s - loss: 0.0015 - 78ms/epoch - 843us/step
92/92 - 0s - loss: 0.0015 - 78ms/epoch - 845us/step
92/92 - 0s - loss: 0.0015 - 79ms/epoch - 859us/step
92/92 - 0s - loss: 0.0015 - 78ms/epoch - 848us/step
92/92 - 0s - loss: 0.0015 - 78ms/epoch - 844us/step
92/92 - 0s - loss: 0.0015 - 78ms/epoch - 852us/step
92/92 [==============================] - 0s 563us/step
44/44 [==============================] - 0s 453us/step
Train Score: 20.58 RMSE
Test Score: 55.99 RMSE对测试数据集的预测再次变得更糟。 这是更多证据表明需要额外的训练时期。