一、实验设计DOE

1. 在建模软件中进行参数化

2. 设计变量的参数范围

3. 试验设计类型选择

（1）CCD 中心成分设计

其样本点包括一个中心点，输入变量轴的端点以及水平因子点。默认选项 (Design Type) 为Auto-Defined，如果输入变量为5个采用 G-Optimal填充，否则采用 VIF-optimal填充。此方法的另外两个选项， Rotatable选项是一个5水平试验取样方法， Face-Centered选项则退化为一个3水平试验取样方法。如果缺省选项造成后续响应面的拟合效果不佳时，可以考虑采用Rotatable选项。

这是最常用的DOE方法。CCD方法随着输入变量的增多，形成的部分因子样本点数遵循公式 N=1+2n+2n−f ,其中 f 为部分因子个数，n为输入参数个数，N为形成的样本点个数。

航空航天用的多，样本点分布类型：常用“自动定义的”，求解精度：可旋转的[标准、加强]>VIF最佳>G最佳>面心的

（2）OSFD最佳空间填充设计

OSF更适合于更为复杂的响应面算法，如Kriging,Non-Parametric Regression 以及NeuralNetworks等。OSF的一个弱点是不一定能取到端点（角点）附近的样本，因此会影响到这些区域的响应面质量，尤其当样本点数量较少时。

这个方法采用最少的设计点填充设计空间。在空间中均匀的生成样本点，样本覆盖面比较全。在较少变量的情况下适用OSF得到的输出量范围相较于CCD更小，对优化结果有所限制。

样本点分布设计类型：“最大嫡”最精确

样本类型：选择“自动选择”就行。完全二次多项式的精度>纯二次多项式>线性模型

样本数量：20左右个调节。

（3）Box-Behnker设计

此方法相比其他方法试验次数少，效率较高，各个因素不会同时处于高水平。可以避免极端因素，化工应用较多。

（4)自定义

此方法允许用户创建自己的DOE算法，可以直接创建设计点或者导入CSV数据文件的设计点。可以从外部导入设计点

（+抽样）： 

此方法包含Custom 方法的功能，并且允许自动添加DOE样本点以有效地填充设计空间。比如，DOE列表最初可以是从前一次分析中导入的设计点组成，或是用其他方法(如CCD、OSF等)形成，可以自动添加新的样本点来完成采样，新添加的样本点时会考虑已有设计点的位置。

这种方法下，还需要输入Total Number of Samples（即总的样本点数），如总的样本点数小于已有的样本点数，则不会添加新的样本点。默认值为CCD方法的样本点数。

（5）SGI 稀疏网格初始化

Sparse Grid Initialization 方法为稀疏网格（Sparse Grid）类型的响应面的专用DOE方法，是基于设定的要求的自适应方法，可在输出变量梯度较大位置处自动细化设计点数量以提高响应面精度。

用的比较少，但写论文用的比较多，局部自动细化样本点。但是试验点数量少、稀疏，精确度不高，普适性不强。

（6）超拉丁采样细化

Latin Hypercube Sampling Design 方法是一种修正的蒙特卡洛抽样方法，它可以有效避免样本点的聚集。（蒙特卡洛抽样方法见：一文看懂蒙特卡洛采样方法 - 知乎）这个方法有一个缺点是在响应面角落处不一定有样本点，这个会影响响应面的质量。

CCD Samples ：会形成与CCD DOE方法同样数量的设计点。
Linear Model Samples：形成线性响应面所需数量的样本点。
Pure Quadratic Model Samples：用于形成纯二次（没有交叉项）响应面所需数量的样本点。
Full Quadratic Samples：用于形成完全二次响应面所需数量的样本点。
User-Defined Samples ：选项由用户指定所需的样本点数量。如选择了此选项则后续需要指定Number of Samples选项。

• 手动输入试验设计点

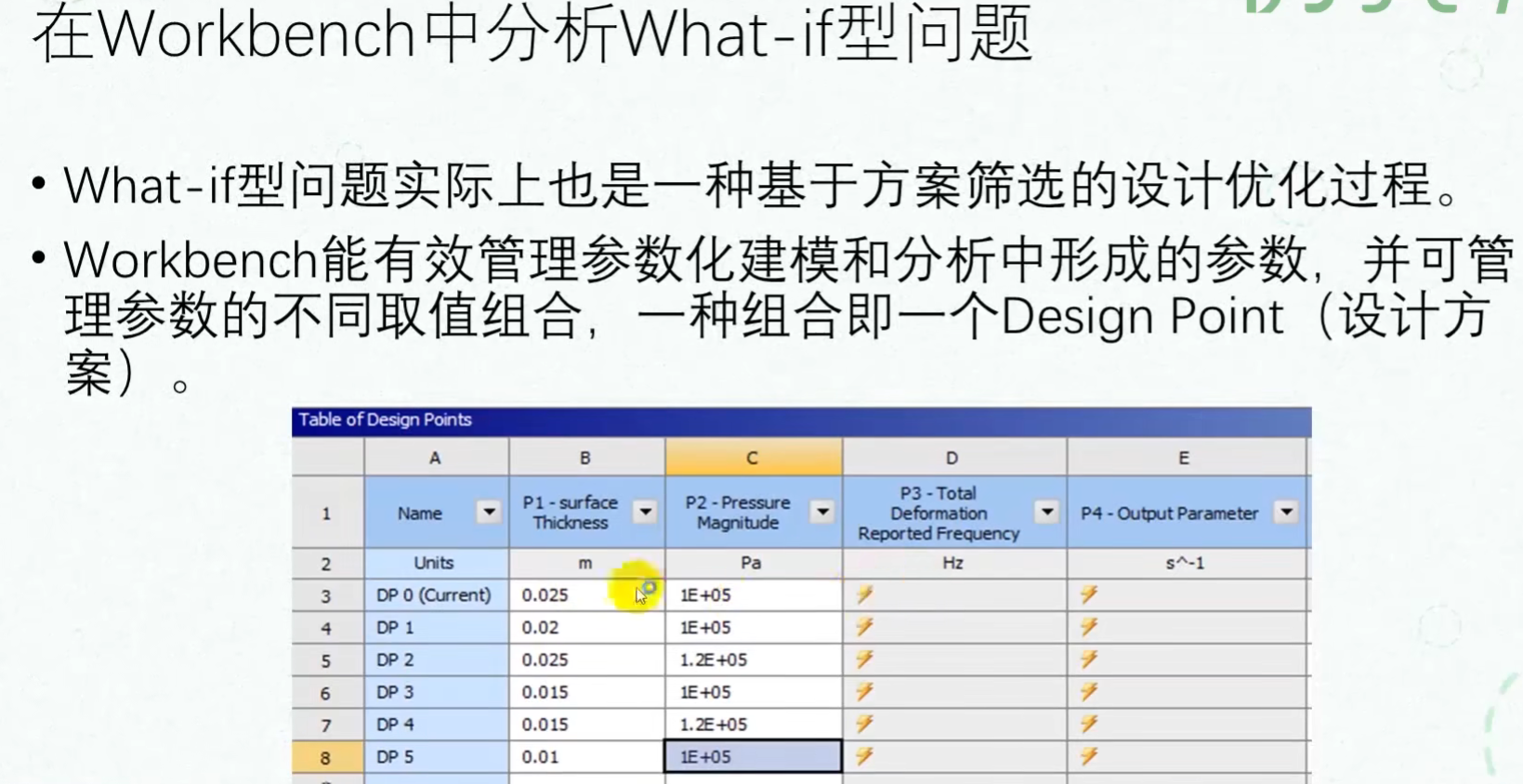
5. 选择“更新”

二、响应面

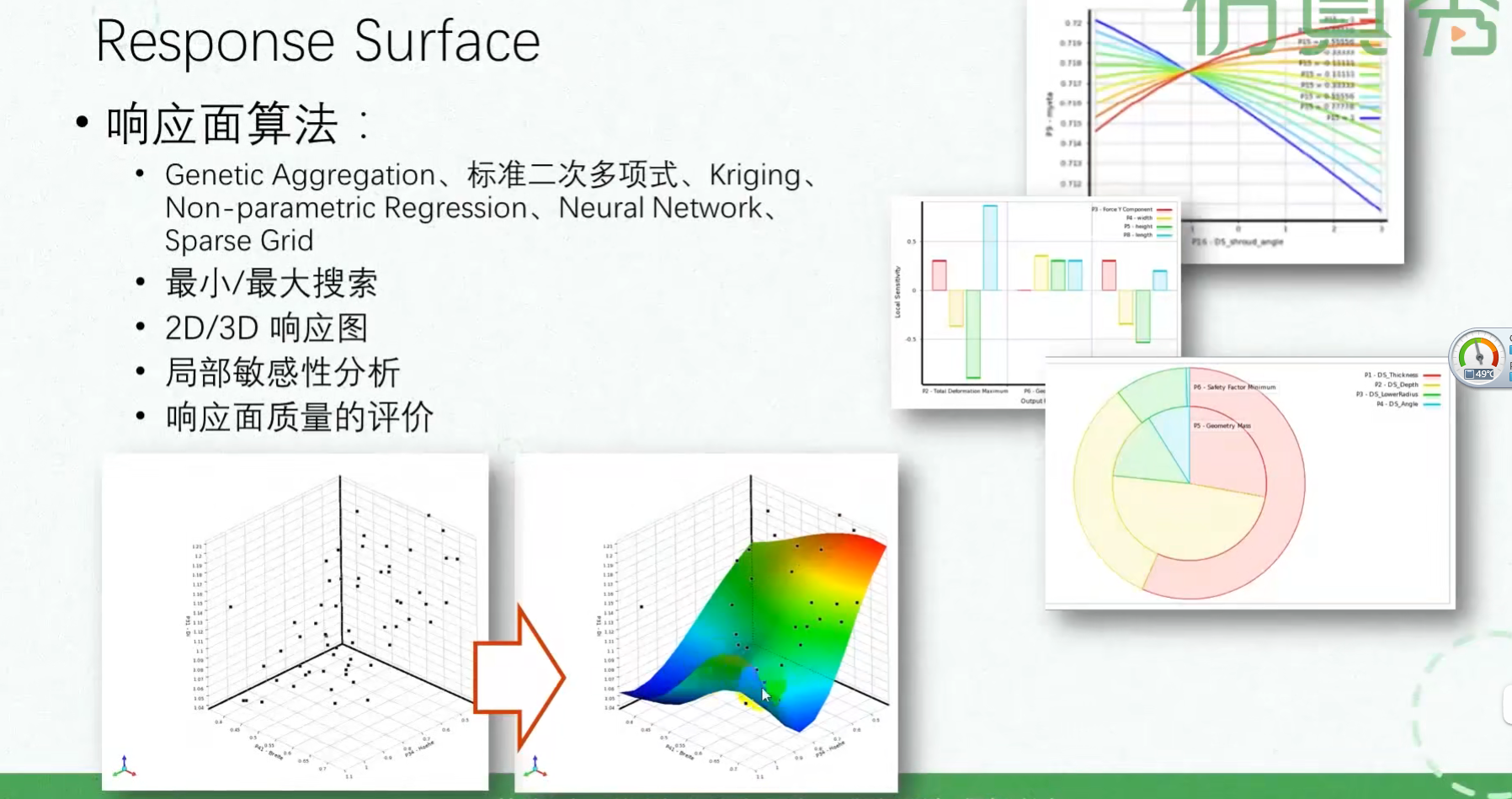
响应面生成结果中，在Min-Max Search中直接查看取极值的参数；Refinement Points中可以添加自定义的参数组；Goodness of Fit 通过验证点检验回归分析的拟合质量，Verification Points 为验证点的参数，也可以添加别的验证点；Response Point下面是四种结果图：2参数三维热图、目标量-输入变量敏感性柱图、敏感性曲线、蛛网图（多目标优化适用）。

1.响应曲面类型：

概述：先用标准二级响应面，再用Kriging，再用神经网络和非参数回归，最后再用稀疏网格初始化。

（1）遗传聚合

（2）标准二阶响应面

Standar Response Surface 采用回归分析确定近似的二次响应函数，回归分析结果用Goodness of fit来评价。它的输入输出关系线性或者光滑、连续。

（3）Kriging插值法

样本点很多时，很适合用于几何参数的评估。结果嘈杂时不能用。可有细化点。

（4）非参数回归

适用于非线性模型。结果嘈杂的时候用，但是计算过程慢。

（5）神经网络

适用于高度非线性模型，可用于验证别的响应面结果，但是只有一个隐含层。通过哟更改隐含子数量3，前面设计点数量来调节优化效果

（6）稀疏网络

对连续参数的求解，通过更改相对误差、细化点、最大细化点。

2. 验证点

两三个。不参与响应面的构建。

3. 细化点

参与响应面的构建

4. 本地敏感度：

5. 响应面评估

GOF

三、优化

1. 优化方法选择

（1）响应面

（2）直接优化

（3）ASO，AMO

2. 目标函数和约束条件设置

复合变量、最小化、最大化、目标值

3. 选择“更新”

4. 结果

（1）候选方案

（2）tradeoff

（3）samples

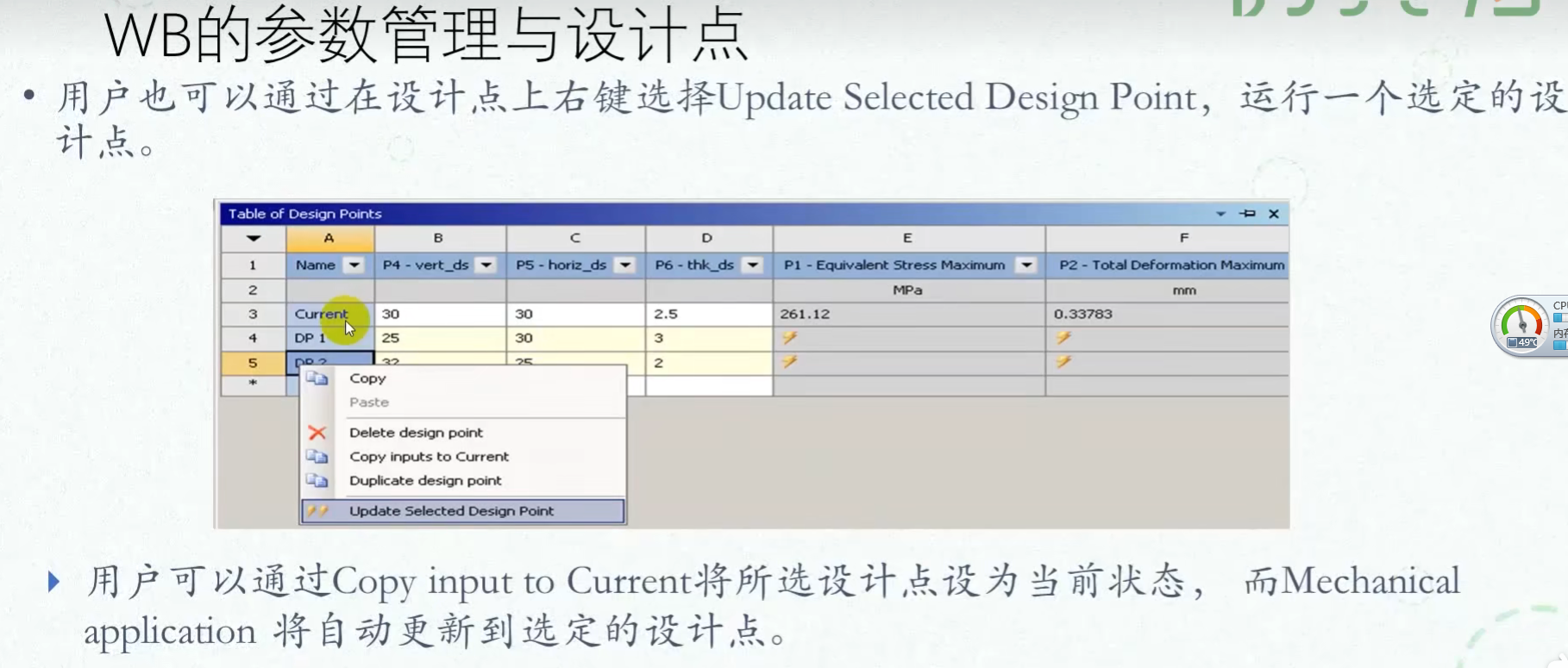
（4）从优化候选点中创建新的设计点并更新至原仿真模块

步骤：候选点——右键：插入到设计点——新设计点：右键：更新输入到当前——更新所选设计点

current指的是当前仿真模块的输入参数状态。

四、相关性分析

如果优化参数太多，可以用相关性分析找出影响较大的参数。

很多时候，优化参数数目庞大，会使得采样点数据急剧增加，导致仿真时间极长。因而需要从优化采样点中剔除不需要的采样点。对于一个输出参数，输入参数的重要性是由它们的相关性来决定的。参数相关性研究的作用，一方面是可帮助分析人员决定哪些输入参数对设计的影响最重要（或最不重要），相关性矩（correlation matrix）可帮助用户识别出被认为是不重要的输入参数；另一方面还可以识别参数之间的关系，如：是线性的关系或是二次关系。

在 Correction Type中可以选择相关性类型

（1）Spearman：使用样本变量值的排序（秩）计算相关系数，适用于具有非线性单调变化函数关系的变量之间的相关性， 被认为是更精确的方法。二次相关分析可给出任意一对变量之间的判定系数，此系数越接近1，则二次相关的效果越好。这些系数构成了判定矩阵（Determination Matrix），此矩阵是非对称的，这与相关性矩阵（Correlation Matrix）不同。
（2）Pearson：采用变量值来计算相关性系数，用于关联具有线性关系的变量。可计算给出相关性系数矩阵（Correlation Matrix）及判定系数矩阵（Determination Matrix）。

更新完后得到结果：

A、相关性矩阵图

相关性矩阵图可以直观显示参数之间的相关性，相关系数越接近±1，表明相关程度越高。

B、相关性散点图

可以设定参数和目标量，并且通过散点图自动拟合曲线，Linear Trend为线性拟合，Quadratic Trend为二次方拟合。通过拟合曲线可以检索目标量和优化参数之间的关系，不过一般很少有存在非常完美的线性or二次方关系。

C、判定矩阵图

0到1代表相关性的增强，相比于相关性矩阵去了绝对值。

D、判定系数矩阵图

通过设置阈值，可以过滤掉对于目标影响不大的因素。

E、敏感性图

给出各个输入变量对每一个选择的响应变量的总体敏感性柱状图。这种敏感性的统计是基于Spearman秩相关系数分析，同时考虑了输入参数变化范围和输出参数关于输入参数变化程度两方面的因素。我个人觉得这张图是最直观全面的，通过它来选取优化参数即可。

作者：Sheeper-Xu
链接：https://zhuanlan.zhihu.com/p/561072635
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。