马尔科夫决策过程(MDP) : GridWord(DP)

有限马尔可夫决策过程：5x5 Gridworld

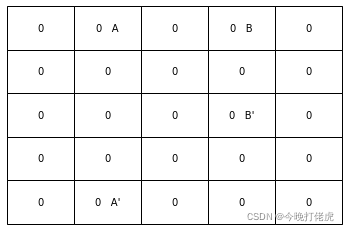
    Grid World是一个矩形的网格世界环境，它包含了一个有限的马尔可夫决策过程，在这个环境中每个网格表示一个状态$state$,每个状态可以执行的动作集合是 A = { 上，下，左，右 } A =\{上，下，左，右\} A={上，下，左，右}四个动作。每个动作会让$agent$沿着动作的方向移动一个单位距离，同时获得一个即时奖励0，如果$agent$在网格的边界上朝着离开网格的方向移动，会得到一个负激励-1，同时状态（位置）不发生变化。有两个特殊的状态$A和B$,$A$状态执行任意动作都会得到一个正向激励+10，后继状态为$A^{\prime }$，$B$状态执行任意动作都会得到一个正向激励+5,后继状态为$B^{\prime }$。

Grid World 环境初始化

• $|\mathcal{S}|$ : $5\times 5$
• $s_A=[0,1]$ : 特别状态 $A$,坐标即状态
• $s_A^{\prime }=[4,1]$ : $A^{\prime }$
• $s_B=[0,3]$ ：特别状态 $B$
• $s_B^{\prime }=[2,3]$ : $B^{\prime }$
• $\gamma =0.9$ ：discount rate
• $\mathcal{A}=[[0,-1],[-1,0],[0,1],[1,0]]$ : 动作集合：
  • $a=[0,-1]$ ：$s+a=s^{\prime }$,y坐标-1相上移动1
• $p(a|s)=0.25$ : 在状态$s$采取动作$a$的概率

initi_env = np.zeros((WORLD_SIZE,WORLD_SIZE)).astype(int)

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.table import Table

WORLD_SIZE = 5         # grid_world's size
A_POS = [0, 1]         # A location in grid world
A_PRIME_POS = [4, 1]   # A' location 
B_POS = [0, 3]         # B location
B_PRIME_POS = [2, 3]   # B' location
DISCOUNT = 0.9         # discount rate

# left, up, right, down
ACTIONS = [np.array([0, -1]),
           np.array([-1, 0]),
           np.array([0, 1]),
           np.array([1, 0])]
ACTION_PROB = 0.25

状态更新：$step(s,a)\to s^{\prime },r$

def step(state, action):
    if state == A_POS:
        return A_PRIME_POS, 10
    if state == B_POS:
        return B_PRIME_POS, 5

    next_state = (np.array(state) + action).tolist()
    x, y = next_state
    if x < 0 or x >= WORLD_SIZE or y < 0 or y >= WORLD_SIZE:
        reward = -1.0
        next_state = state
    else:
        reward = 0
    return next_state, reward

根据贝尔曼方程估计$state\_value$

$$v_{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })],for\_all\_s\in \mathcal{S}$$

• $\pi$ : 策略，状态到每个可能选择动作的概率映射
• $v_{\pi }$ : 在遵循策略$\pi$的条件下,状态$s$的状态值
• $\pi (a|s)$ : 遵循策略$\pi$,当状态为$s$时，采取动作$a$的概率
• $p(s^{\prime },r|s,a)$ : 状态转移概率,$s\to s^{\prime }$

在Grid World环境中给定状态和动$s$和动作$a$的情况下,后继状态$s^{\prime }$和立即奖励$r$是确定的,可以忽略转移概率$p$,简化为:

$$v_{\pi }(s)=\sum _a\pi (a|s)[r+\gamma v_{\pi }(s^{\prime })]$$

1. 随机策略：每个动作选择概率相同
2. 贪心策略： v ∗ ( s ) = max ⁡ π v π ( s ) = max ⁡ a { r + γ v ∗ ( s ′ ) , a ∈ A } v^*(s) = \max\limits_{\pi} v_{\pi}(s) = \max\limits_{a}\{r+\gamma v^*(s'), a \in \mathcal A \} v∗(s)=πmax​vπ​(s)=amax​{r+γv∗(s′),a∈A}

随机策略

$$v_{k+1}(s)=\sum _a\pi (a|s)\times (r+\gamma v_k(s^{\prime }))$$

• $k$ : 迭代更新的次数
• $v_{k+1}(s)$ : 状态$s$第$k+1$次状态值

def random_policy():
    # 初始化状态值为 0
    value = np.zeros((WORLD_SIZE, WORLD_SIZE))
    value_history = [value]
    while True:
        new_value = np.zeros_like(value)
        for i in range(WORLD_SIZE):
            for j in range(WORLD_SIZE):
                for action in ACTIONS:
                    (next_i, next_j), reward = step([i, j], action)
                    # 动作概率 *（即时奖励 + 折扣* 后继状态值）
                    new_value[i, j] += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])
        # 判断是否value收敛
        if np.max(np.abs(new_value - value)) < 1e-4:
            break
        value = new_value
        value_history.append(value)
    return value_history

状态值的更新过程：同步更新

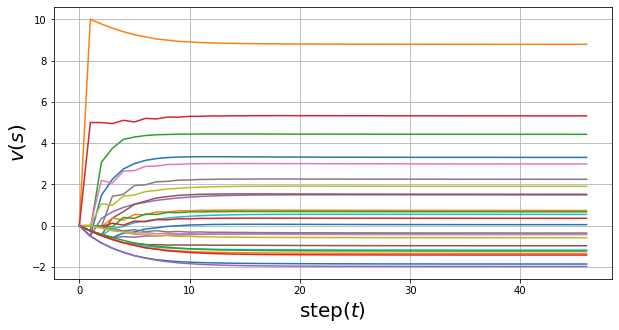
状态值：

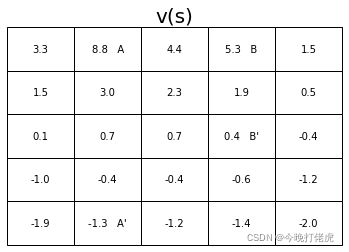
    从上图中可以发现，$A$的期望回报略低于它的及时奖励，这是因为$A$总是跳转到$A^{\prime }$,$A^{\prime }$在网格的边界处，得到一个负激励的概率比较大。$B$的期望汇报略高于它的及时奖励，这是因为$B^{\prime }$只有一个方向距离边界较近，所以获得负激励的概率较小。

贪心策略

$$v_{\ast }(s)=\underset{a}{\max }{q}_{{\pi }_{\ast }}(s,a)$$

def optimal_policy():
    value = np.zeros((WORLD_SIZE, WORLD_SIZE))
    value_history = [value]
    while True:
        new_value = np.zeros_like(value)
        for i in range(WORLD_SIZE):
            for j in range(WORLD_SIZE):
                # 记录每个动作的value
                values = []
                for action in ACTIONS:
                    (next_i, next_j), reward = step([i, j], action)
                    # 及时奖励 + 折扣 * 后继状态值
                    values.append(reward + DISCOUNT * value[next_i, next_j])
                new_value[i, j] = np.max(values)
        if np.max(np.abs(new_value - value)) < 1e-4:
            break
        value = new_value
        value_history.append(value)
    return value_history

状态值的更新过程：

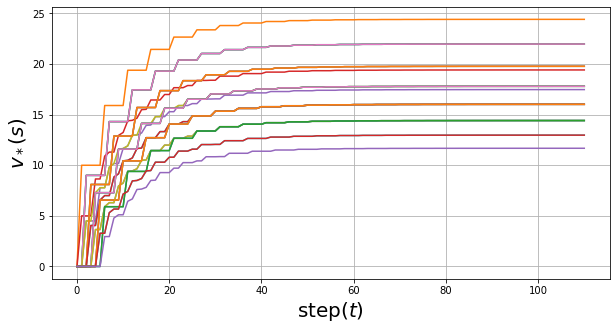
大约经过110次迭代后收敛，收敛后的状态值：

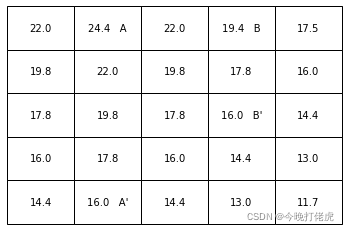
加速状态值的收敛 “in place"更新方法 异步更新

while True:
    new_value = np.zeros_like(value)
    for i in range(WORLD_SIZE):
        for j in range(WORLD_SIZE):
        # 记录每个动作的value
            values = []
            for action in ACTIONS:
                (next_i, next_j), reward = step([i, j], action)
                # 及时奖励 + 折扣 * 后继状态值
                values.append(reward + DISCOUNT * value[next_i, next_j])
            new_value[i, j] = np.max(values)
    value = new_value

    上面的迭代策略估计中，用了两个变量value和new_value,分别来表示两个相邻的旧状态值和新状态值。上面更新方法中，每计算出一个状态的值后，存入new_value,直到全部状态计算完成，才更新value中的值，这会影响到状态值收敛的速度。"in place"方式就是，每计算出一个状态值，就更新到value,做到及更即用。

随机策略,In place

不同更新方式，值函数收敛速度对比

def random_policy():
    # 初始化状态值为 0
    value = np.zeros((WORLD_SIZE, WORLD_SIZE))
    value_history = [np.copy(value)]
    while True:
        for i in range(WORLD_SIZE):
            for j in range(WORLD_SIZE):
                expect_value = 0
                for action in ACTIONS:
                    (next_i, next_j), reward = step([i, j], action)
                    # 动作概率 *（即时奖励 + 折扣* 后继状态值）
                    expect_value += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])
                value[i, j] = expect_value
        value_history.append(np.copy(value))
        # 判断是否value收敛
        if np.max(np.abs(value_history[-1] - value_history[-2])) < 1e-4:
            break
    return value_history

贪心策略

def optimal_policy():
    # 初始化状态值为 0
    value = np.zeros((WORLD_SIZE, WORLD_SIZE))
    value_history = [np.copy(value)]
    while True:
        for i in range(WORLD_SIZE):
            for j in range(WORLD_SIZE):
                values = []
                for action in ACTIONS:
                    (next_i, next_j), reward = step([i, j], action)
                    # 及时奖励 + 折扣 * 后继状态值
                    values.append(reward + DISCOUNT * value[next_i, next_j])
                value[i, j] = np.max(values)
        value_history.append(np.copy(value))
        # 判断是否value收敛
        if np.max(np.abs(value_history[-1] - value_history[-2])) < 1e-4:
            break
    return value_history

"in place"方式对随机策略影响不大，但是在最优策略下，收敛时间是原来的五分之一左右。