目录
前言
此篇文章是刷题系列的第一篇,此后该系列会随着小嘟对语言知识的学习而改变语言的使用!刚开始是用C语言来解决哦~可能顺序有些复杂,再加上数据结构的使用不熟练,还请大家见谅!
方法可能并不是小嘟想出来的,但还是想能够分享给大家!让更多的人知道!
1、LeetCode 448 找到所有数组中消失的数字
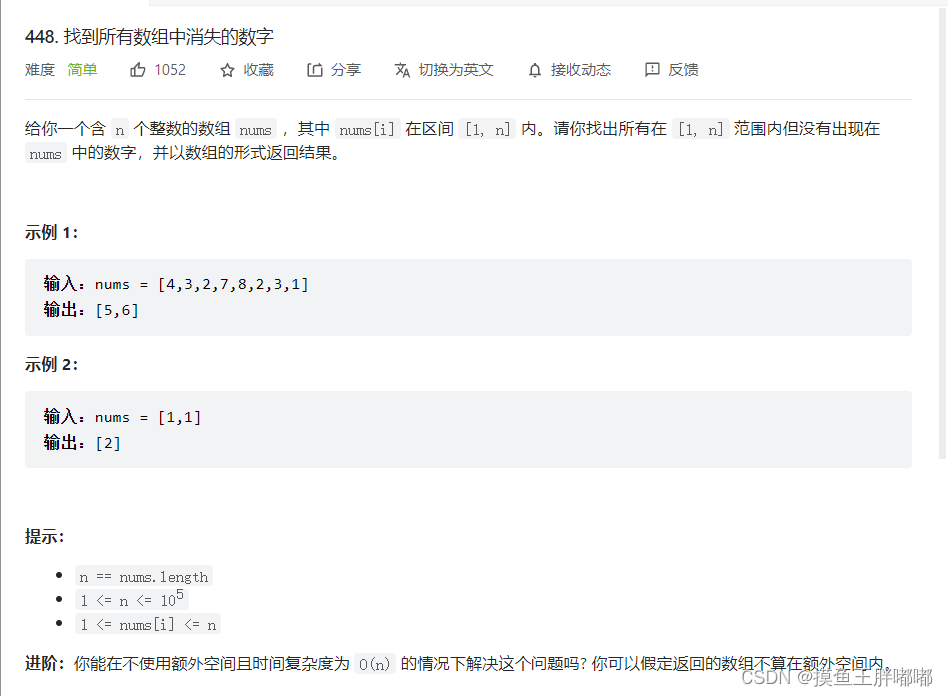
思路:原地修改
我们可以用一个哈希表记录数组nums中的数字,由于数字范围均在[1,n]中,记录数字后我们再利用哈希表检查[1,n]中的每一个数是否出现,从而找到缺失的数字。
由于数字范围均在 [1,n]中,我们也可以用一个长度为 nn 的数组来代替哈希表。这一做法的空间复杂度是 O(n) 的。我们的目标是优化空间复杂度到 O(1)。
注意到nums 的长度恰好也为 n,能否让nums 充当哈希表呢?
由于nums 的数字范围均在 [1,n]中,我们可以利用这一范围之外的数字,来表达「是否存在」的含义。
具体来说,遍历nums,每遇到一个数 x,就让 nums[x−1] 增加 n。由于 nums 中所有数均在 [1,n] 中,增加以后,这些数必然大于 n。最后我们遍历 nums,若 nums[i] 未大于 n,就说明没有遇到过数 i+1。这样我们就找到了缺失的数字。
注意,当我们遍历到某个位置时,其中的数可能已经被增加过,因此需要对 n 取模来还原出它本来的值。
可能讲的有点抽象,小嘟画一张图帮助理解吧!
此处举例以[1,2,2,3,3,4,7,8]来帮助理解!
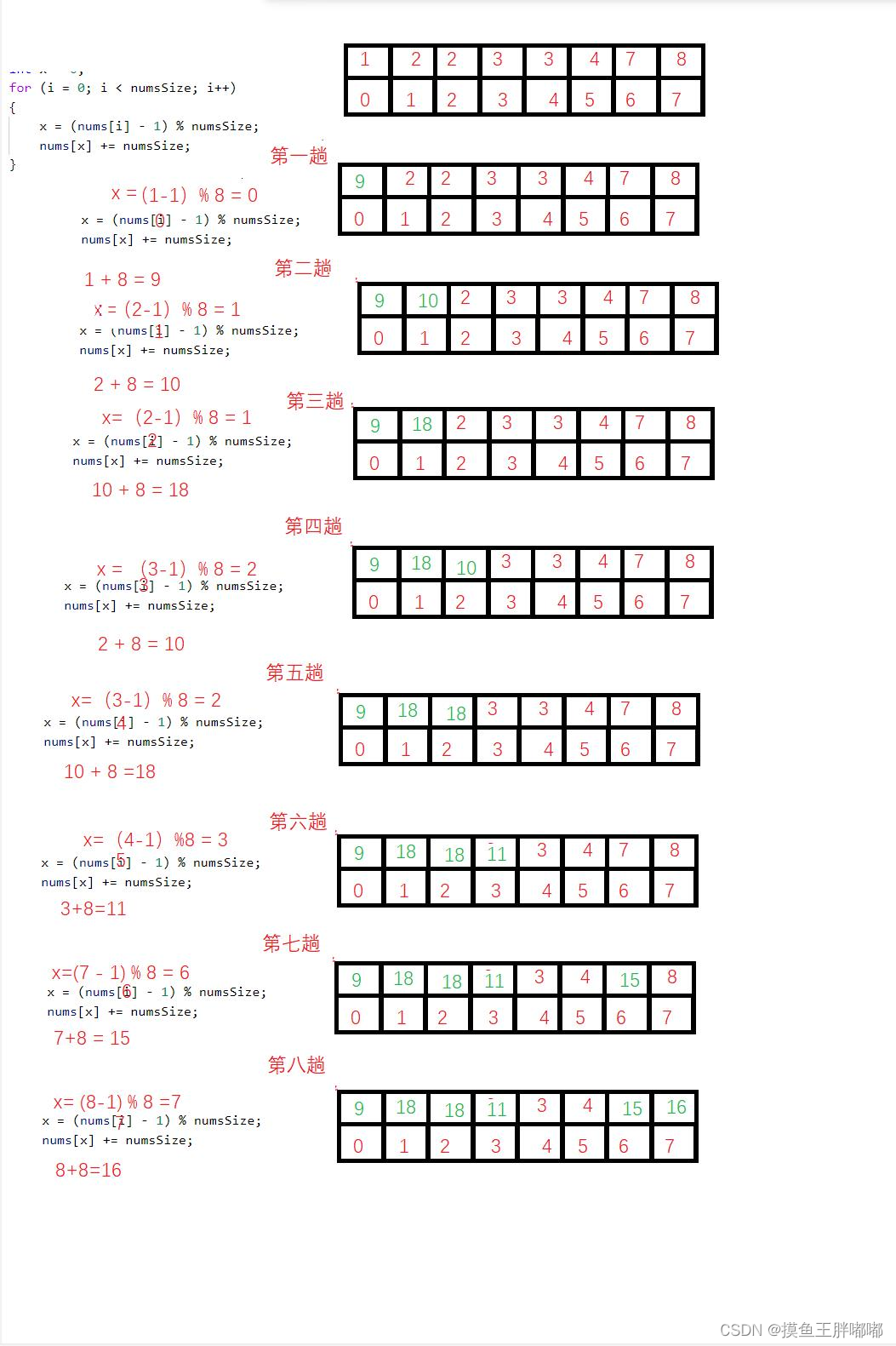
像这样就找出来下标为4,5的数值小于numsSize了,我们只需要把这两个下标+1赋给新的数组就可以了!
代码示例:
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){
int i = 0;
int x = 0;
for (i = 0; i < numsSize; i++)
{
x = (nums[i] - 1) % numsSize;
nums[x] += numsSize;
}
int* findDisappearedNumbers = (int*)malloc(sizeof(int) * numsSize);
*returnSize = 0;
for (i = 0; i < numsSize; i++)
{
if (nums[i] <= numsSize)
{
findDisappearedNumbers[(*returnSize)++] = i + 1;
}
}
return findDisappearedNumbers;
}
2、LeetCode 238 除自身以外数组的乘积

思路:乘积 = 当前数左边的乘积 * 当前数右边的乘积
如标题一样:乘积 = 当前数左边的乘积 * 当前数右边的乘积
举个例子:
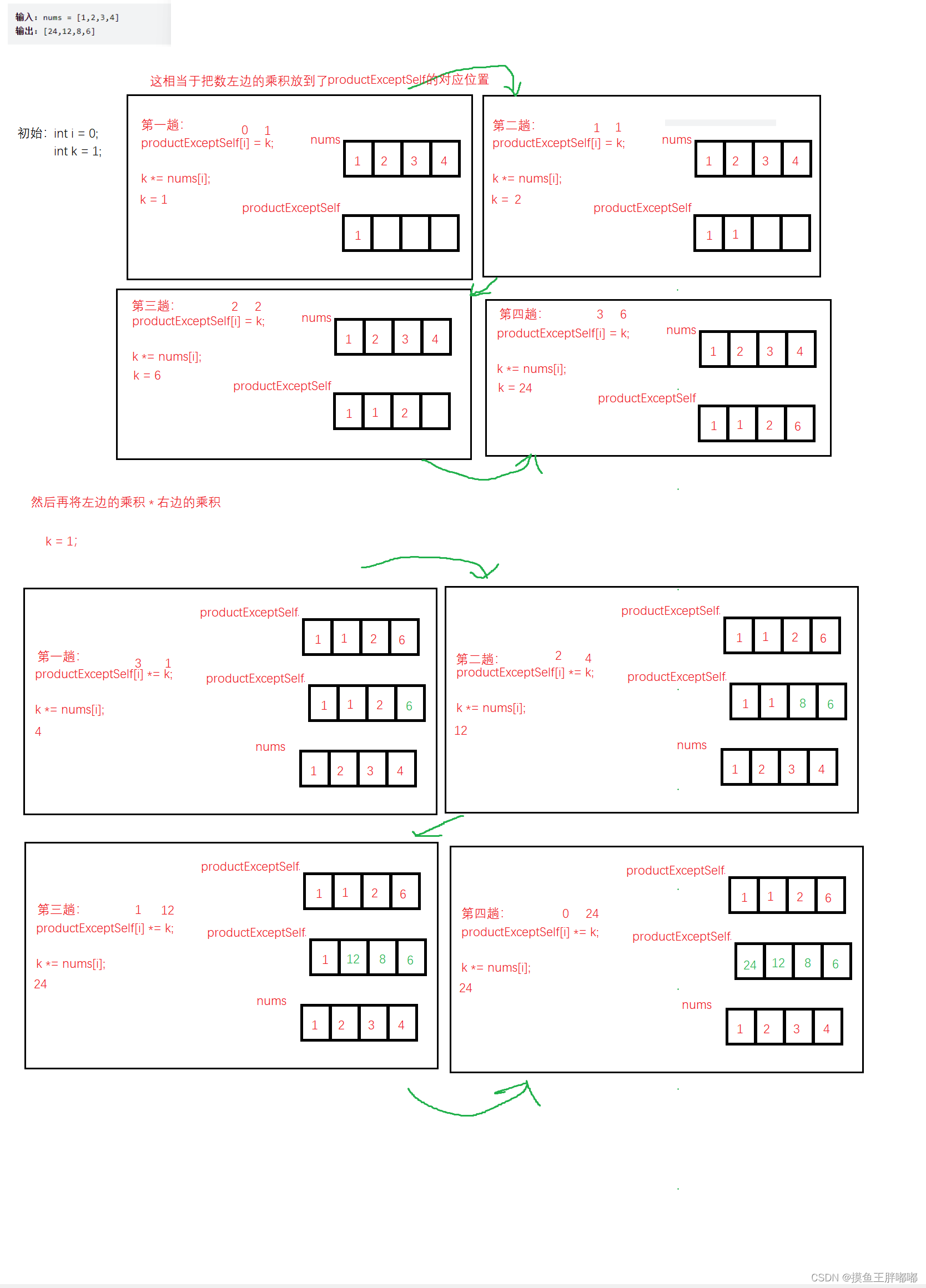
像这样就能够实现题目的要求了!
代码示例:
int* productExceptSelf(int* nums, int numsSize, int* returnSize){
int* productExceptSelf = (int*)malloc(sizeof(int) * (numsSize));
int i = 0;
int k = 1;
for(i = 0; i < numsSize; i++){
productExceptSelf[i] = k;
k *= nums[i];
}
k = 1;
for(i = numsSize- 1; i >= 0; i--){
productExceptSelf[i] *= k;
k *= nums[i];
}
* returnSize = numsSize;
return productExceptSelf;
}
3、LeetCode 728 自除数
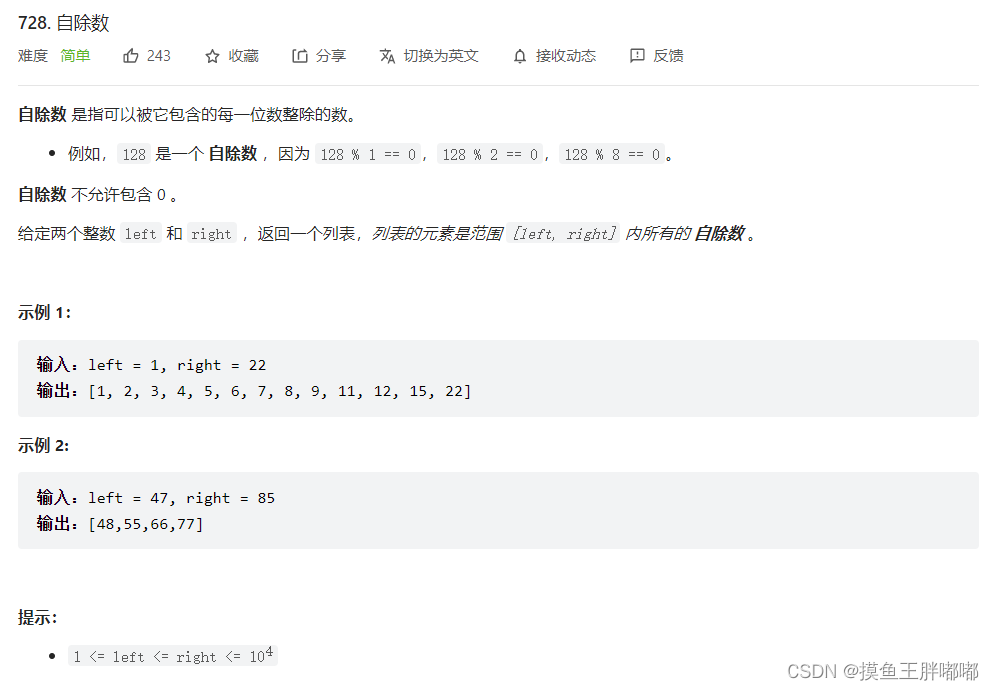
思路:直接判断
遍历范围 [left,right] 内的所有整数,分别判断每个整数是否为自除数。
根据自除数的定义,如果一个整数不包含 0 且能被它包含的每一位数整除,则该整数是自除数。判断一个整数是否为自除数的方法是遍历整数的每一位,判断每一位数是否为 0 以及是否可以整除该整数。
遍历整数的每一位的方法是,每次将当前整数对 10 取模即可得到当前整数的最后一位,然后将整数除以 10。重复该操作,直到当前整数变成 0时即遍历了整数的每一位。

代码示例:
int isSelfDividing(int num)
{
int temp = num;
while (temp > 0) {
int digit = temp % 10;
if (digit == 0 || num % digit != 0) {
return 0;
}
temp /= 10;
}
return 1;
}
int* selfDividingNumbers(int left, int right, int* returnSize){
int * selfDividingNumbers = (int *)malloc(sizeof(int) * (right - left + 1));
int i = 0;
int pos = 0;
for(i = left; i <= right; i++)
{
if(isSelfDividing(i))
{
selfDividingNumbers[pos++] = i;
}
}
* returnSize = pos;
return selfDividingNumbers;
}
4、LeetCode 169 多数元素
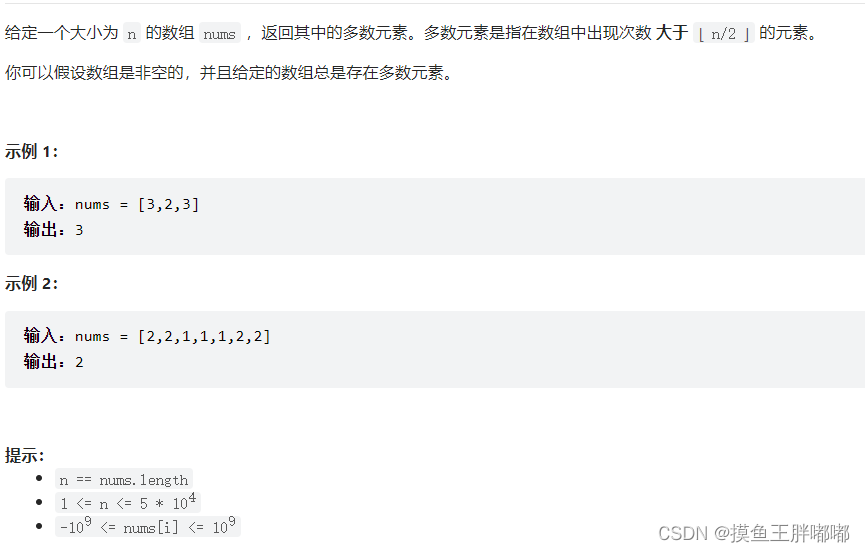
思路:排序
这是一种简单的方法:
如果将数组nums中的所有元素按照递增或者递减的顺序排序,那么下标为[n/2]的元素(下标从0开始)一定是众数。

代码示例:
int cmp(const void *e1,const void *e2)
{
return *(int*)e1 - *(int*)e2;
}
int majorityElement(int* nums, int numsSize){
qsort(nums,numsSize,sizeof(int),cmp);
return nums[numsSize / 2];
}
5、LeetCode 724 寻找数组的中心下标

思路:前缀法
记数组的全部元素之和为total,当遍历到第 ii 个元素时,设其左侧元素之和为 sum,则其右侧元素之和为total−numsi−sum。左右侧元素相等即为sum=total−numsi−sum,即2×sum+numsi=total。
当中心索引左侧或右侧没有元素时,即为零个项相加,这在数学上称作「空和」(empty sum)。在程序设计中我们约定「空和是零」。
代码示例:
int pivotIndex(int* nums, int numsSize){
int total = 0;
for (int i = 0; i < numsSize; i++)
{
total += nums[i];
}
int sum = 0;
for (int i = 0; i < numsSize; i++)
{
if (2 * sum + nums[i] == total)
{
return i;
}
sum += nums[i];
}
return -1;
}
6、LeetCode 349 两个数组的交集
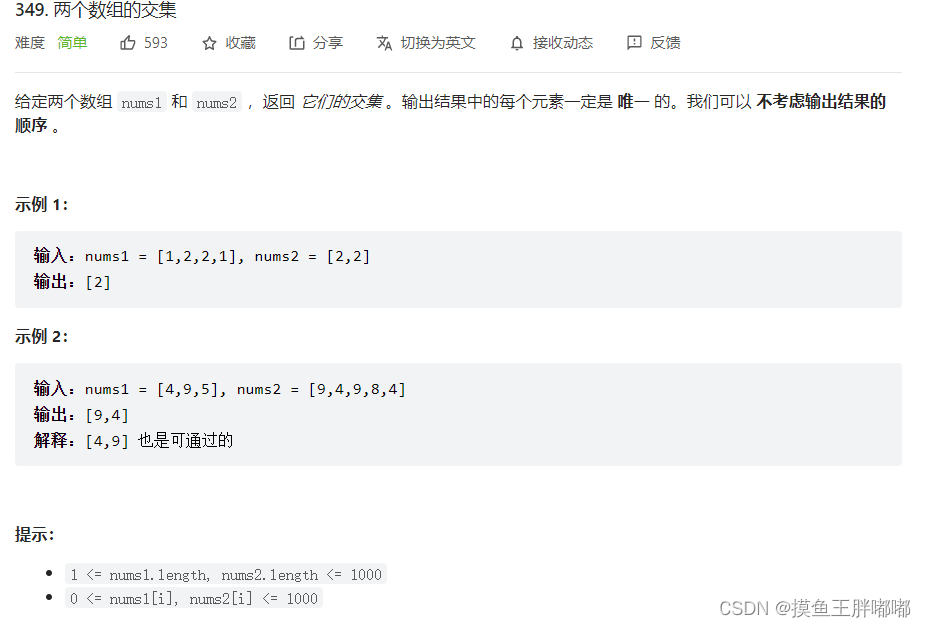
思路:排序+双指针
如果两个数组是有序的,则可以使用双指针的方法得到两个数组的交集。
首先对两个数组进行排序,然后使用两个指针遍历两个数组。可以预见的是加入答案的数组的元素一定是递增的,为了保证加入元素的唯一性,我们需要额外记录变量pre 表示上一次加入答案数组的元素。
初始时,两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字,如果两个数字不相等,则将指向较小数字的指针右移一位,如果两个数字相等,且该数字不等于 pre ,将该数字添加到答案并更新pre 变量,同时将两个指针都右移一位。当至少有一个指针超出数组范围时,遍历结束。
举个例子:
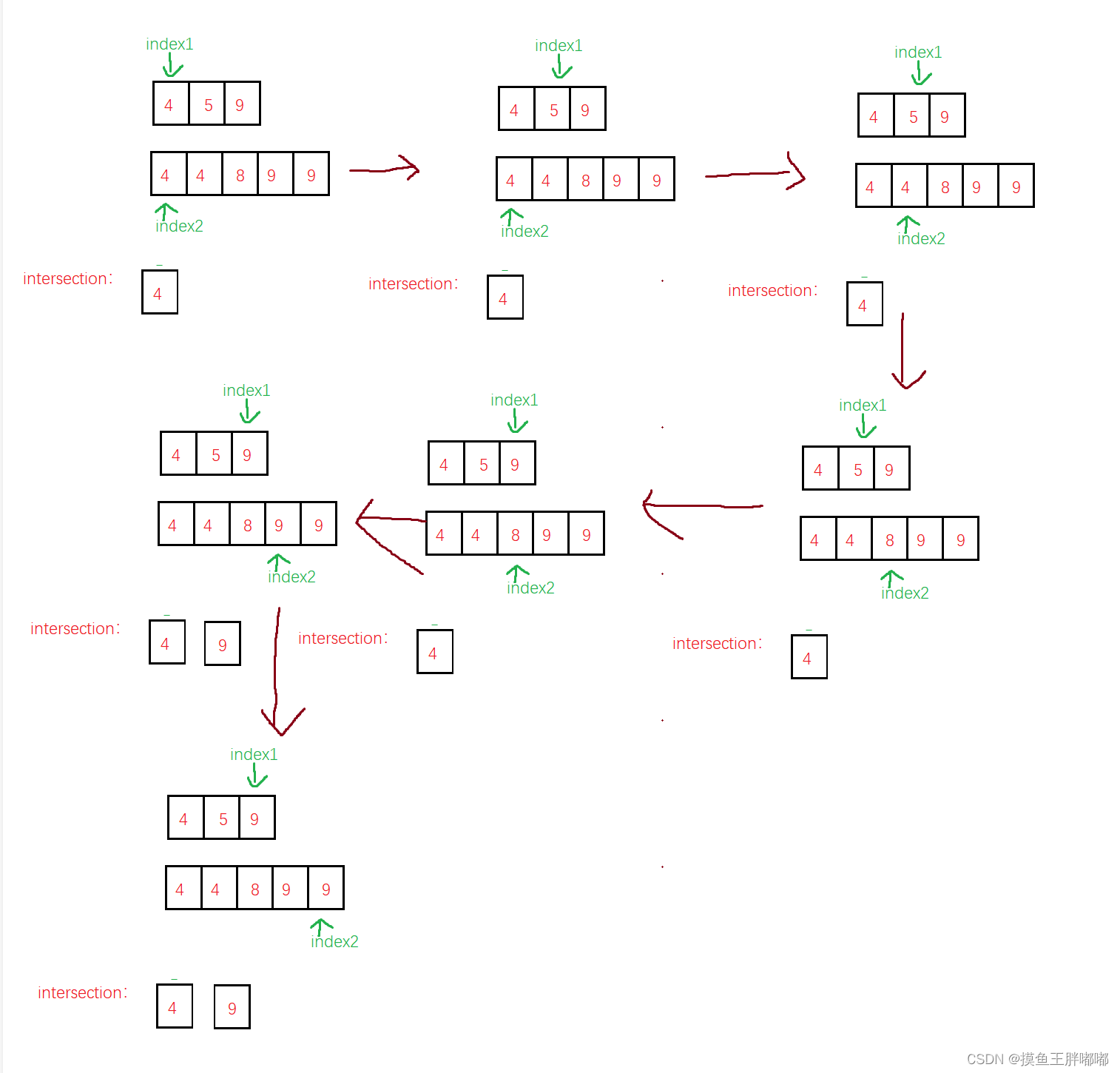
代码示例:
int cmp(void* a, void* b)
{
return *(int*)a - *(int*)b;
}
int* intersection(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize){
qsort(nums1, nums1Size, sizeof(int), cmp);
qsort(nums2, nums2Size, sizeof(int), cmp);
*returnSize = 0;
int index1 = 0, index2 = 0;
int* intersection = malloc(sizeof(int) * (nums1Size + nums2Size));
while(index1 < nums1Size && index2 < nums2Size)
{
int num1 = nums1[index1];
int num2 = nums2[index2];
if(num1 == num2)
{
if(!(*returnSize) || num1 != intersection[(*returnSize) - 1])
{
intersection[(*returnSize)++] = num1;
}
index1++;
index2++;
}else if(num1 < num2)
{
index1++;
}else
{
index2++;
}
}
return intersection;
}
7、LeetCode 747 至少是其他数字两倍的最大值

思路:遍历
遍历数组分别找到数组的最大值m1和次大值m2 。如果 m1 ≥m2 × 2 成立,则最大值至少是数组其余数字的两倍,此时返回最大值的下标,否则返回−1。
为了返回最大值的下标,我们需要在计算最大值的同时记录最大值的下标。
代码示例:
int dominantIndex(int* nums, int numsSize){
if(numsSize == 1)
{
return 0;
}
int a = -1, b = 0;
for(int i = 1; i < numsSize; i++)
{
if (nums[i] > nums[b])
{
a = b;
b = i;
} else if (a == -1 || nums[i] > nums[a]) {
a = i;
}
}
return nums[b] >= (nums[a] * 2) ? b : -1;
}
8、LeetCode 面试题05.06.整数转换
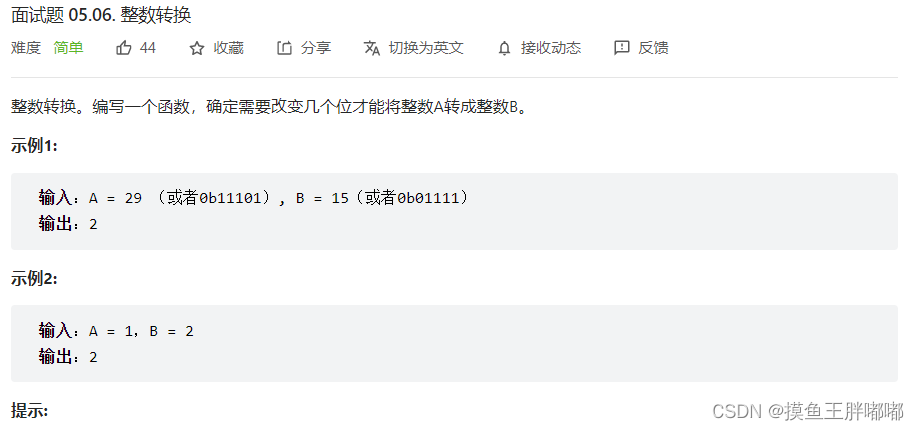
思路:异或
1.异或
2.统计二进制个数:
首先把n &(按位与)1,判断n的最低位是不是1,
接着把1左移一位得到2 ,再 &(按位与)n,
就能判断n的次第位是不是为1
反复左移运算,每次都能判断n的其中一位是不是1。
代码示例:
int convertInteger(int A, int B){
int i = 0;
int count = 0;
int tmp = A ^ B;
for(i = 0; i < 32; i++)
{
if((tmp>>i)&1 == 1)
{
count++;
}
}
return count;
}
9、LeetCode 645 错误的集合
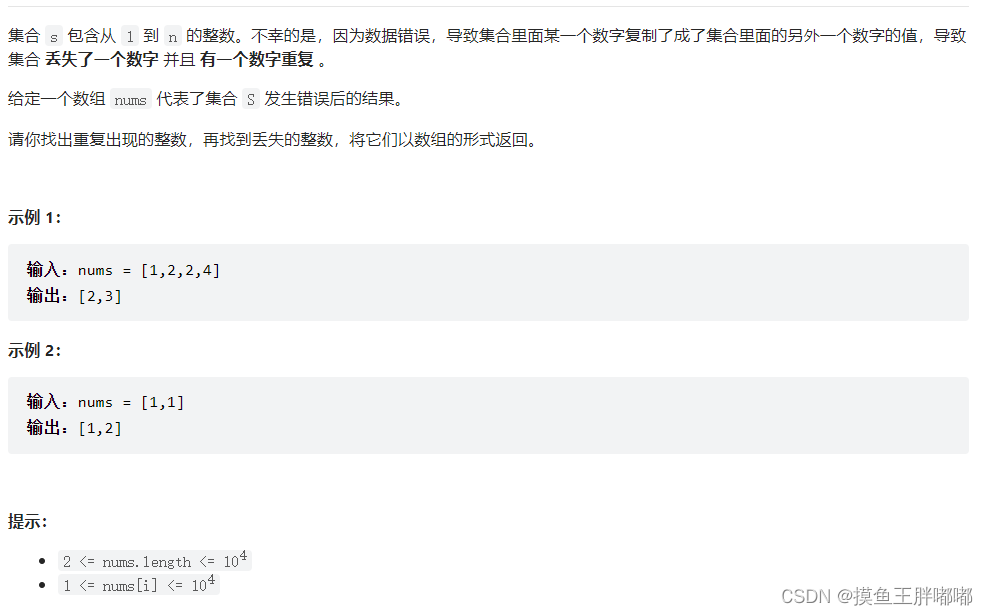
思路:排序

代码示例:
int cmp(int* a, int* b) {
return *a - *b;
}
int* findErrorNums(int* nums, int numsSize, int* returnSize) {
int* errorNums = malloc(sizeof(int) * 2);
*returnSize = 2;
qsort(nums, numsSize, sizeof(int), cmp);
int prev = 0;
for (int i = 0; i < numsSize; i++)
{
int curr = nums[i];
if (curr == prev)
{
errorNums[0] = prev;
}else if (curr - prev > 1)
{
errorNums[1] = prev + 1;
}
prev = curr;
}
if (nums[numsSize - 1] != numsSize) {
errorNums[1] = numsSize;
}
return errorNums;
}
总结
今天就先到这了,如果大家对某些题有着更好的解法,欢迎在评论区进行讨论哦~