一、介绍

        邻接多重表是用于构建无向图的一种存储结构。我们知道，我们构建一个无向图可以利用邻接矩阵来实现，但是我们可以注意到，为了表现出“无向”的特点，我们在为邻接矩赋值的时候需要进行两次“连接”，就是将邻接矩阵中对称的位置都需要赋值为同一个值，这样显然十分消耗时间和空间。

        在前面介绍过的十字链表我们可以知道，每个链表头都有两个指针，一个用来指向第一条以自身为弧尾的弧，一条用来指向第一条以自身为弧头的弧，当然这是在构建有向图的情况下。如果现在我们要构建一个无向图呢，很显然，我们并不需要两个指针用来指向与自身连接的边，因为不管自己是作为头还是尾，在无向边中都是无意义的，因此邻接多重表就出现了。

        邻接多重表与十字链表最主要的区别就是顶点只有一个指针，这个指针指向一条边，这条边就可以表示和自身相连的点，并且使用头插法就可以很简单地实现点与边的连接，在下文中我会一一进行阐述。

二、类

使用多重邻接表构建无向图与十字链表类似，包含了顶点类和边类（十字链表存储的是有向图，因此在十字链表中包含的是弧类），以及一个无向图类。

边类：

class line
{
    public:
    int vertex1,vertex2;//分别表示边所连接的两个节点
    line* headlink,*taillink;//分别表示指向有着相同头/尾顶点的下一条边
}

顶点类：

class vertex
{
    public:
    int data;//顶点包含的数据
    line* firstline;//指向顶点所连接的第一条边
};

无向图类：

class undigraph
{
    public:
    vertex* listhead;//链表头
    int vertexnum=0,linenum=0;//初始化无向图的定点数为0，边数为0
    void createundigraph();//创建无向图
    int gethead(int value);//得到链表头
};

其中无向图类包含了两个成员函数，分别是用于创建无向图的createundigraph()和用来根据用户输入内容从而定位到链表头下标的函数gethead()

createundigraph函数:

为了便于理解，我画了几张图用来方便理解：

下面的五张图分别表示了5组顶点的连接，分别是(0,1)(1,2)(2,3)(3,0)(0,2)

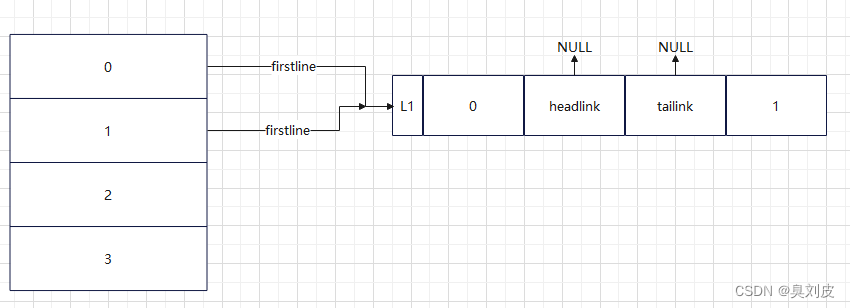
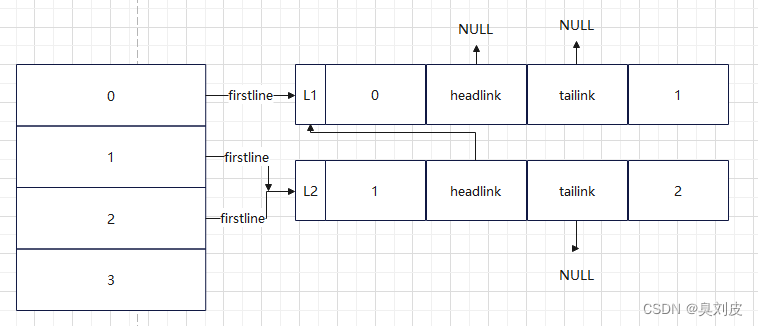
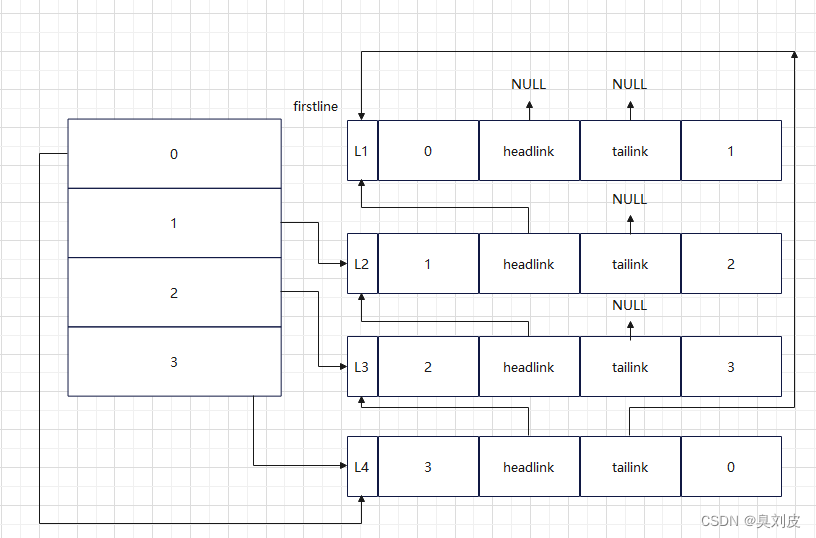
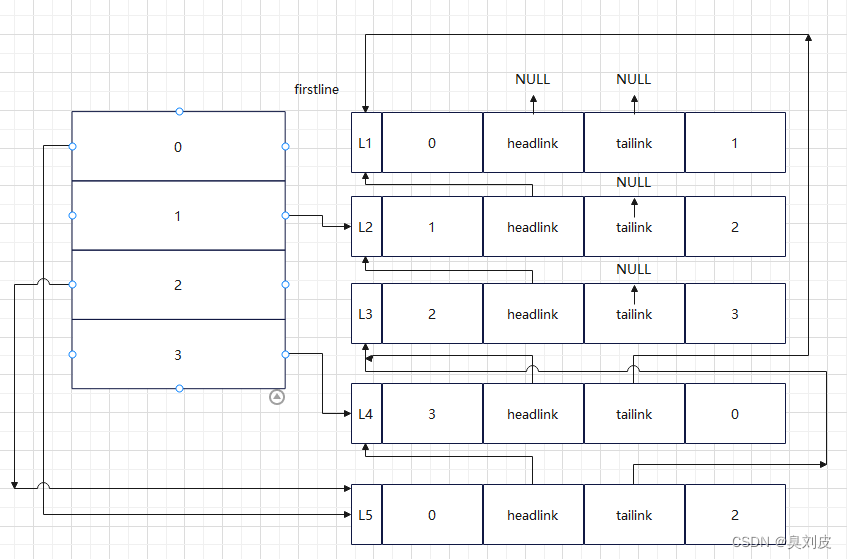
 在理解完连接的过程和原理之后下面附上代码:

void undigraph::createundigraph()
{
    cout<<"请输入无向图的顶点数："<<endl;
    cin>>vertexnum;
    cout<<"请输入无向图的边数:"<<endl;
    cin>>linenum;
    listhead=new vertex[vertexnum];
    for (int i = 0; i < vertexnum; i++)
    {
        cout<<"请输入顶点"<<i<<"的数据:"<<endl;
        cin>>listhead[i].data;
        listhead[i].firstline=NULL;
    }
    for (int i = 0; i < linenum; i++)
    {
        int v1,v2;
        line* newline=new line;//创建一条新边并分配内存
        memset(newline,0,sizeof(line));//为新边内存区内的数据初始化为0
        cout<<"请输入第"<<i+1<<"条边的第一个顶点:"<<endl;
        cin>>v1;
        newline->vertex1=v1;
        cout<<"请输入第"<<i+1<<"条边的第二个顶点:"<<endl;
        cin>>v2;
        newline->vertex2=v2;
        //下面的四步就是线与点连接的关键
        newline->headlink=listhead[gethead(v1)].firstline;
        listhead[v1].firstline=newline;//头插法
        newline->taillink=listhead[gethead(v2)].firstline;
        listhead[v2].firstline=newline;
        
    }
    
    
}

gethead函数:

int undigraph::gethead(int value)
{
    int j;
        for (j = 0; j < vertexnum; j++)
        {
            if (listhead[j].data==value)
            {
                break;
            }
            
        }
        cout<<"得到的链表头为"<<j<<endl;
        return j;
}

三、总结

        总的来说邻接多重表和十字链表在某种意义上是邻接矩阵和邻接表的“升级版”，需要好好的去理解吸收才能对图的存储有更好的理解。

这是本人的第三篇csdn博客，大家如果喜欢的话可以点点赞，有没写好的请多多指正！