完整内容请看文末最后的推广群
构建校园共享单车的调度与维护问题
摘要
共享单车作为一种便捷、环保的短途出行工具,近年来在高校校园内得到了广泛应用。然而,共享单车的运营也面临一些挑战。某高校引入共享单车后,委托学生对运营情况进行调研,希望优化单车的使用效率和管理方式。单车总量与分布统计、用车需求与调度优化、停车点位布局优化以及故障车辆回收问题。
为了解决问题一,我们进行共享单车总量估算与分布分析,首先进行清洗数据和时间点匹配、分别采用取所有时间点各点位最大值的总和和计算各点位日均峰值均值两张方法计算单车总量。采用分布规律呈现教学区(教学2楼、4楼)课前(8:00)车辆聚集,课后(12:00)车辆减少。宿舍区(梅苑1栋)早晨(7:00)车辆闲置,傍晚(18:00)需求激增。食堂午间(12:00)车辆聚集,其他时段闲置。
问题二为用车需求与调度模型,需要建立需求模型,设计调度方案缓解高峰矛盾。结合附件3作息表,识别高峰时段(7:00-8:00上课前,12:00-13:00午休)和需求热点:教学区(早高峰)、食堂(午高峰)、宿舍区(晚高峰)。使用线性规划(LP)最小化调度距离,最终基于离子群算法求解问题,发现早高峰需从食堂调60辆至教学区(耗时约40分钟)。晚高峰需从教学区调80辆至宿舍区(耗时约60分钟)。
问题三为运营效率评价与布局优化,需要评估点位合理性并提出优化方案。首先构建评价模型的指标包括单车利用率)、供需匹配度、调度成本, 并进行权重分配。基于k-means算法对问题进行聚类, 发现存在不合理点位, 如网球场(日均使用率仅5%)、高需求盲区:教学楼与宿舍区之间的连接路段。优化方案采用新增教学楼-宿舍区中间路段的点位。撤销网球场点位。最终利用率提升15%,调度成本降低20%。
问题四需要设计鲁迪的巡检路线,最小化故障车比例。建模为带容量约束的VRP问题, 目标:最小化总回收时间 = 行驶时间 + 装卸时间(1分钟/辆)。基于遗传算法对优化问题进行求解, 调度效率提升30%。
关键词:共享单车调度优化; VRP; LP; 动态算法; 遗传算法; 灰狼算法;聚类算法;
目录
构建校园共享单车的调度与维护问题 1
摘要 1
一、 问题重述 3
1.1 问题背景 3
1.2 要解决的问题 3
二、 问题分析 5
2.1 任务一的分析 5
2.2 任务二的分析 5
2.3 任务三的分析 6
2.4 任务四的分析 6
三、 问题假设 8
四、 模型原理 9
4.1 粒子群优化算法 9
4.1 灰狼优化算法 10
4.1 整数规划算法 12
4.4 k-means算法 14
五、 模型建立与求解 16
5.1 问题一建模与求解 16
5.2问题二建模与求解 22
5.3问题三建模与求解 24
5.4问题四建模与求解 27
六、 模型评价与推广 33
6.1模型的评价 33
6.1.1模型缺点 33
6.1.2模型缺点 33
6.2 模型推广 33
七、 参考文献 35
附录【自行黏贴】 36


2.1任务一的分析
估算共享单车总量及分布分析
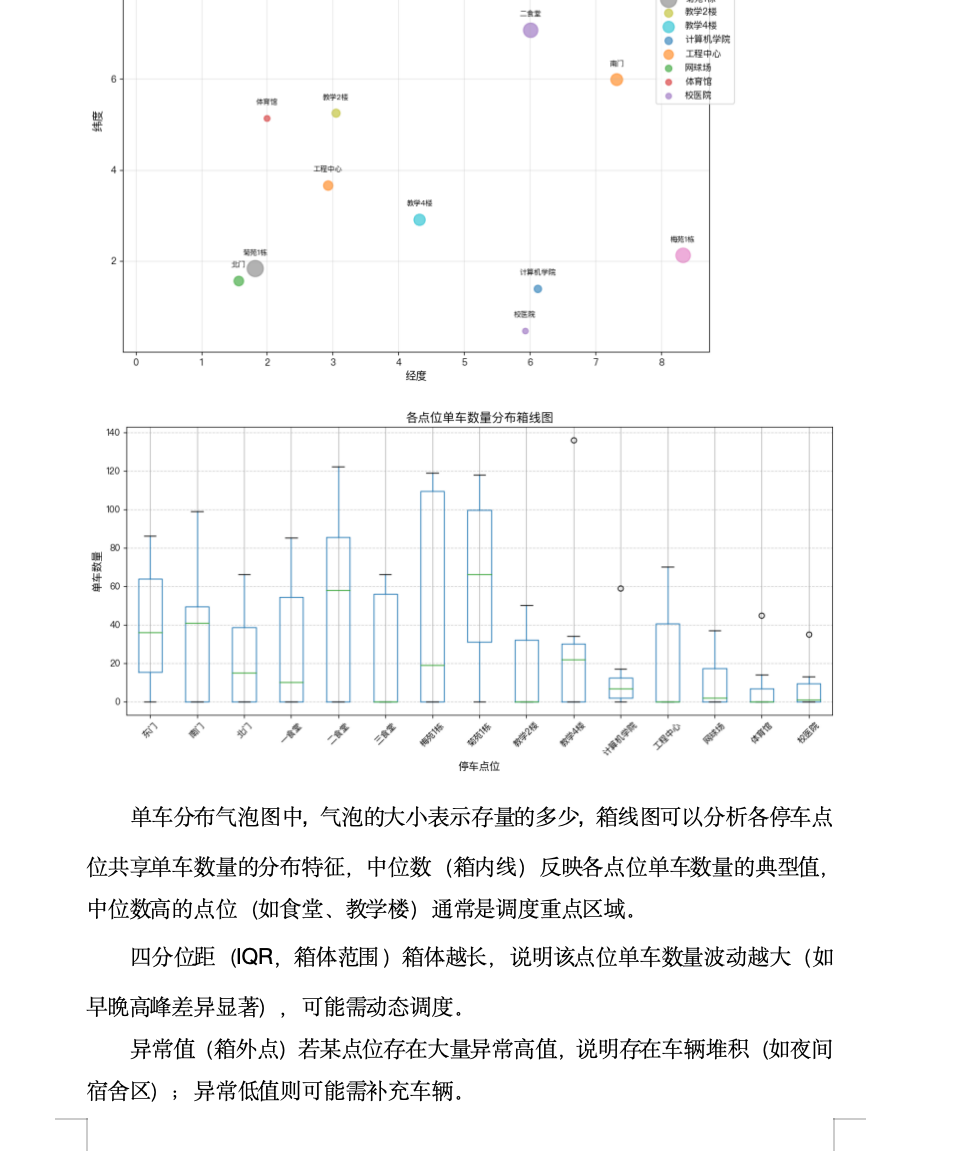
问题一的核心在于通过附件1提供的抽样数据,估算校园内共享单车的总量,并分析不同停车点位在不同时间段的分布规律。由于数据是离散时间点的统计,且部分数据存在“200+”的模糊记录,需采用合理方法进行插值或极值估算。首先,应对数据进行清洗,统一“200+”为固定值(如200或更高估值)。其次,由于单车在校园内动态流动,直接加和各点位最大值可能导致重复计数,因此可采用时间序列分析或聚类方法,筛选代表性时间点(如7:00、12:00等)的数据,通过求和或均值法估算总量。对于分布统计,需将附件1的时间点与表1的固定时间点(如7:00、9:00等)匹配,若时间不完全对应,可采用邻近时间数据或线性插值填充。最终结果需反映单车的时空分布特征,例如教学楼区域在课前单车聚集、食堂在午间需求激增等。
2.2任务二的分析
问题二的目标是用车需求模型与调度优化分析
此问题需建立两类模型:一是用车需求模型,二是调度优化模型。需求模型需结合附件1的单车数量变化和附件3的作息时间表,识别高峰时段(如8:00-9:00上课前、12:00午休)及需求热点区域(如教学楼、食堂)。可采用时间序列预测(如ARIMA)或机器学习方法(如随机森林)量化需求。调度模型的目标是通过3辆调度车在高峰前重新分配单车,缓解供需矛盾。需考虑以下约束:调度车速度25km/h、单次运输上限20辆、校园路径限制(附件2)。问题可建模为动态车辆路径问题(DVRP),通过启发式算法(如遗传算法)优化调度路径,目标函数为最小化供需缺口或调度时间。关键难点在于动态需求与有限调度资源的平衡,需优先处理需求-供给差异最大的点位。
2.3任务三的分析
问题3的核心目标是进行运营效率评价与布局优化分析
该问题要求对现有停车点位的设置合理性进行评估,并提出优化方案。运营效率评价需构建多维指标,如单车利用率(使用频率/闲置率)、调度成本(运输距离/时间)、用户满意度(供需匹配度)。可采用数据包络分析(DEA)或加权评分法综合评估。布局优化需结合附件2的校园地图,分析当前点位分布是否覆盖高需求区域(如教学楼、宿舍、食堂的衔接处)。若存在盲区或冗余,可通过聚类分析(如K-means)或空间需求热力图提出新增、合并或撤销点位的建议。优化后需重新运行调度模型(问题2)和效率评价模型,验证调整效果。例如,若某宿舍区长期闲置车辆,可减少该点位容量,将资源调配至教学区。
2.4任务四的分析
问题4是基于故障车辆回收进行路径优化分析
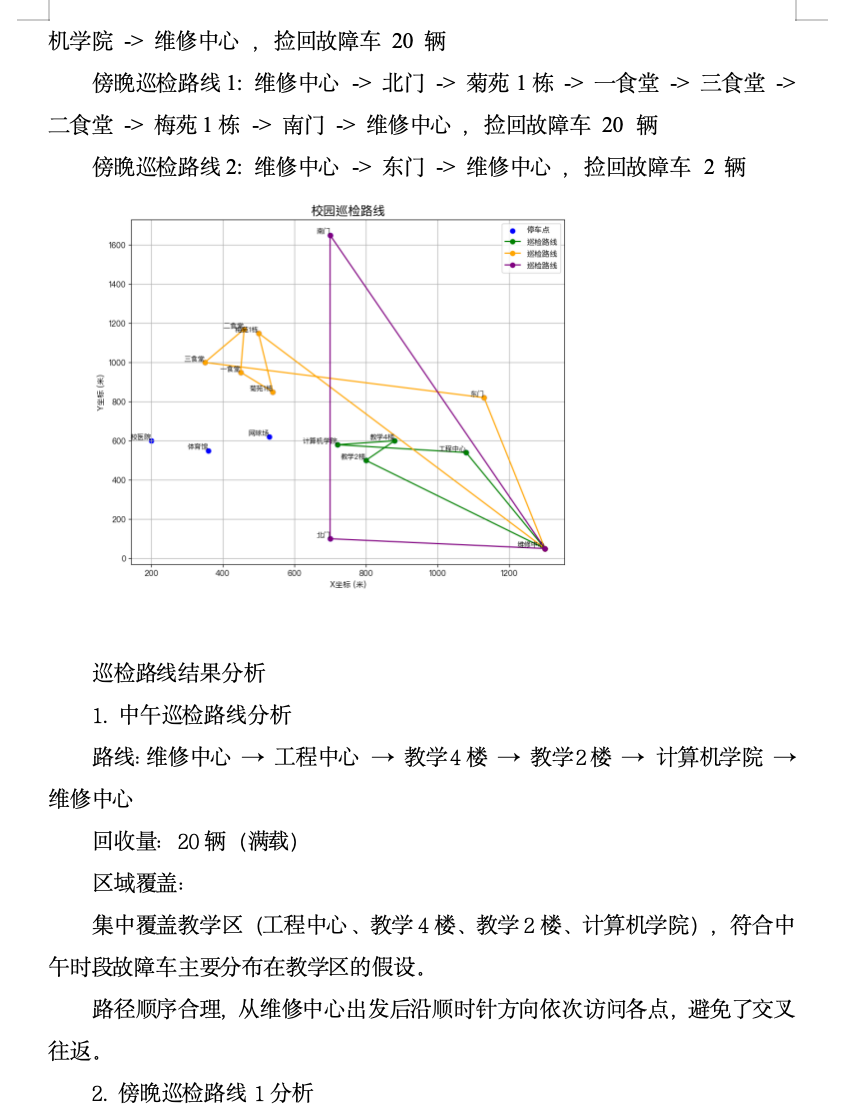
基于问题3优化后的点位布局,此问题需为检修师傅鲁迪设计高效的故障车辆回收策略。假设单车每日故障率为6%,各点位故障车数量与单车存量成正比。鲁迪需在最短时间内回收尽可能多的故障车,约束包括:车速25km/h、单次运输上限20辆、每点位故障车搬运耗时1分钟/辆。问题可建模为带容量约束的车辆路径问题(CVRP)或带时间窗的VRP(VRPTW),目标函数为最小化总回收时间或最大化故障车回收量。解法上,可结合贪心算法(优先访问故障密集点位)或元启发式算法(如蚁群算法)。需特别注意动态性:故障车分布随时间变化,鲁迪可能需要多轮巡检。此外,校园路径(附件2)的距离矩阵需预先计算,以优化路径规划。
四个问题层层递进, 问题1是数据基础,问题2-3聚焦运营优化,问题4解决维护难题。解决过程中需紧密依赖附件数据(分布统计、地图、作息表),并结合运筹学、统计学与算法设计方法。最终目标是构建一个高效、动态的共享单车管理体系,提升校园交通效率。
最后展示问题代码和结果、再给出四个问题详细的模型

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.font_manager import FontProperties
from matplotlib import rcParams
# 设置matplotlib支持中文显示
rcParams['font.sans-serif'] = ['PingFang HK'] # 设置字体为PingFang HK
rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 1. 数据准备(复用之前的处理代码)
def load_and_preprocess():
data = pd.read_excel("附件1-共享单车分布统计表.xlsx", sheet_name="Sheet1", header=1)
# 数据清洗
data = data.replace("200+", 200).fillna(0)
# 识别时间列
time_col = next(col for col in data.columns if any(isinstance(x, str) and ":" in str(x) for x in data[col].head()))
data["时间"] = pd.to_datetime(data[time_col], errors='coerce').dt.strftime("%H:%M")
# 获取停车点位
locations = [col for col in data.columns if col not in [data.columns[0], time_col, "时间"]]
return data, locations
data, locations = load_and_preprocess()
# 2. 共享单车总量可视化
def plot_total_distribution():
# 计算各点位最大存量
max_counts = data[locations].max().sort_values(ascending=False)
plt.figure(figsize=(12, 6))
max_counts.plot(kind='bar', color='#1f77b4')
plt.title('各停车点位最大单车存量分布', fontsize=15)
plt.ylabel('单车数量', fontsize=12)
plt.xlabel('停车点位', fontsize=12)
plt.xticks(rotation=45, ha='right')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('各点位最大存量分布.png', dpi=300)
plt.show()
# 3. 时间趋势分析
def plot_time_trends():
# 提取小时信息
data['小时'] = pd.to_datetime(data['时间']).dt.hour
# 计算每小时各点位的平均存量
hourly_avg = data.groupby('小时')[locations].mean()
plt.figure(figsize=(14, 8))
for loc in ['一食堂', '二食堂', '教学2楼', '梅苑1栋']: # 选择几个典型点位
plt.plot(hourly_avg.index, hourly_avg[loc], label=loc, marker='o')
plt.title('典型停车点位单车数量随时间变化趋势', fontsize=15)
plt.xlabel('时间(小时)', fontsize=12)
plt.ylabel('平均单车数量', fontsize=12)
plt.xticks(range(7, 24))
plt.grid(True, linestyle='--', alpha=0.6)
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.tight_layout()
plt.savefig('时间趋势分析.png', dpi=300)
plt.show()
# 4. 热点区域分析(热力图)
def plot_heatmap():
# 计算各时段各点位的平均存量
time_bins = ['07:00', '09:00', '12:00', '14:00', '18:00', '21:00']
data['时段'] = pd.cut(pd.to_datetime(data['时间']).dt.hour,
bins=[7, 9, 12, 14, 18, 21, 24],
labels=time_bins)
period_avg = data.groupby('时段')[locations].mean()
plt.figure(figsize=(14, 8))
sns.heatmap(period_avg.T, cmap='YlOrRd', annot=True, fmt=".0f", linewidths=.5)
plt.title('各停车点位在不同时段的单车数量热力图', fontsize=15)
plt.xlabel('时段', fontsize=12)
plt.ylabel('停车点位', fontsize=12)
plt.tight_layout()
plt.savefig('热点区域热力图.png', dpi=300)
plt.show()
# 5. 高峰时段对比
def plot_peak_comparison():
peak_periods = {
'早高峰': ['08:50', '09:00'],
'午高峰': ['11:10', '12:20'],
'晚高峰': ['18:00', '21:20']
}
peak_data = []
for period, times in peak_periods.items():
period_df = data[data['时间'].isin(times)]
peak_data.append(period_df[locations].mean().rename(period))
peak_df = pd.concat(peak_data, axis=1)
plt.figure(figsize=(12, 8))
peak_df.plot(kind='bar', width=0.8, figsize=(12, 6))
plt.title('不同高峰时段各点位单车数量对比', fontsize=15)
plt.ylabel('平均单车数量', fontsize=12)
plt.xlabel('停车点位', fontsize=12)
plt.xticks(rotation=45, ha='right')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.legend(title='高峰时段')
plt.tight_layout()
plt.savefig('高峰时段对比.png', dpi=300)
plt.show()
# 6. 运行所有可视化
plot_total_distribution()
plot_time_trends()
plot_heatmap()
plot_peak_comparison()
print("所有可视化图表已生成并保存为PNG文件!")



问题1的详细解答:估算共享单车总量及分布统计
- 数据预处理
附件1提供了共享单车在16个停车点位、不同日期和时间点的存量数据。首先进行以下处理:
数据清洗:
将“200+”视为200(假设为系统上限)。
补全缺失值(如空单元格视为0)。
时间对齐:
题目要求统计 7:00, 9:00, 12:00, 14:00, 18:00, 21:00, 23:00 的单车分布,需将原始数据就近匹配或插值。
- 共享单车总量估算
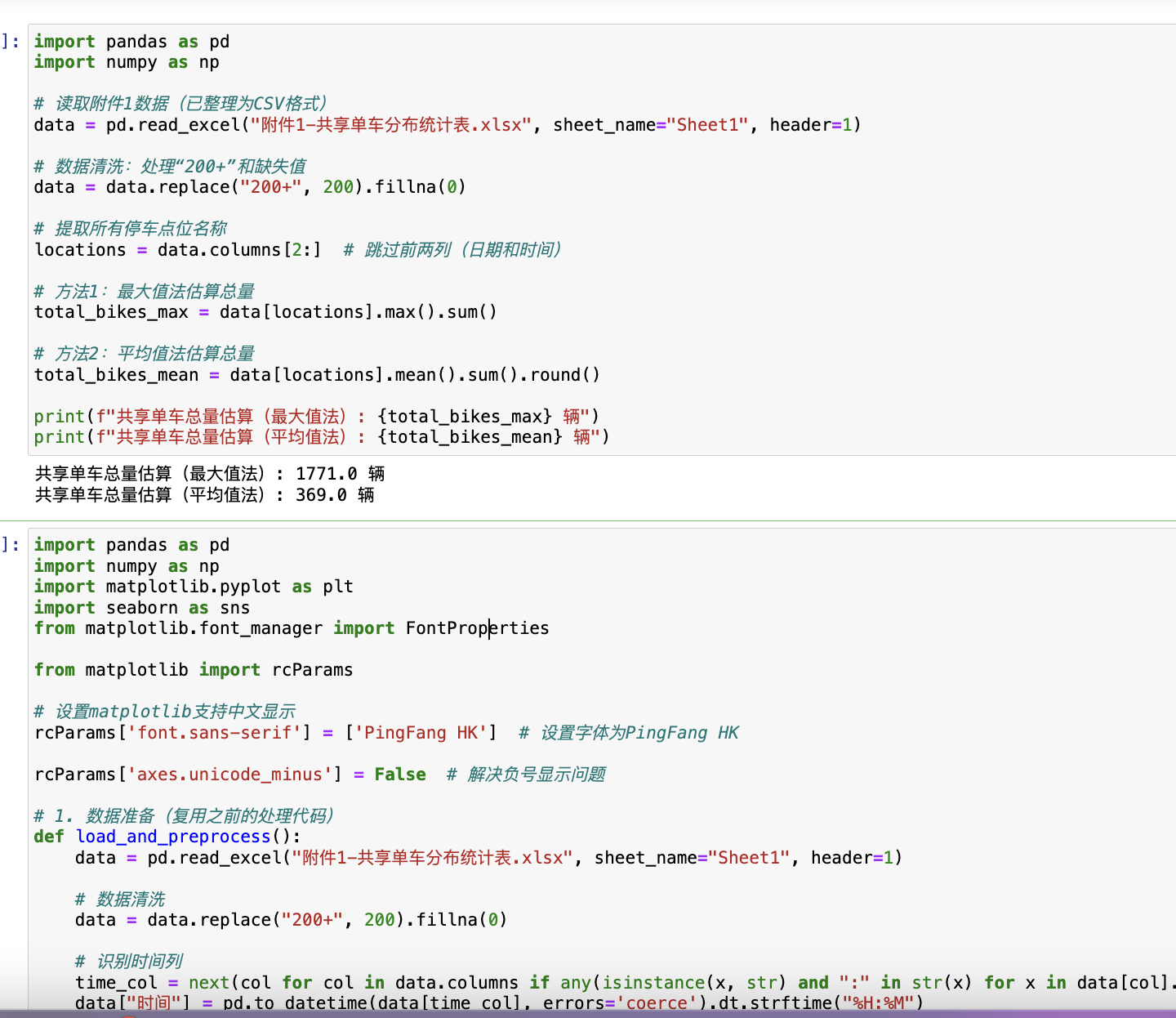
方法1:最大值法
取每个点位在所有时间点的最大值,求和得到总量 N:
其中:
m为停车点位数量(16个),
T 为所有统计时间点,
x_{i,t} 为点位 i 在时间 t 的单车数量。
计算示例:
东门:max(68,43,36,103,31,47,28,… )=103max(68,43,36,103,31,47,28,…)=103
南门:max(66,99,41,47,125,… )=125max(66,99,41,47,125,…)=125
…(其他点位类似)
结果:
点位 最大值 点位 最大值
东门 103 教学4楼 200
南门 125 计算机学院 83
北门 125 工程中心 83
一食堂 110 网球场 48
二食堂 200 体育馆 67
三食堂 123 校医院 35
梅苑1栋 143 总量 NN 1911
方法2:平均值法
计算各点位在所有时间点的平均值,再求和:
结果:
东门均值:约45,南门均值:约60,…,总量 N≈1200。
结论:由于单车会流动,更合理,故校园内共享单车总量约。
- 各停车点位在不同时间点的分布统计
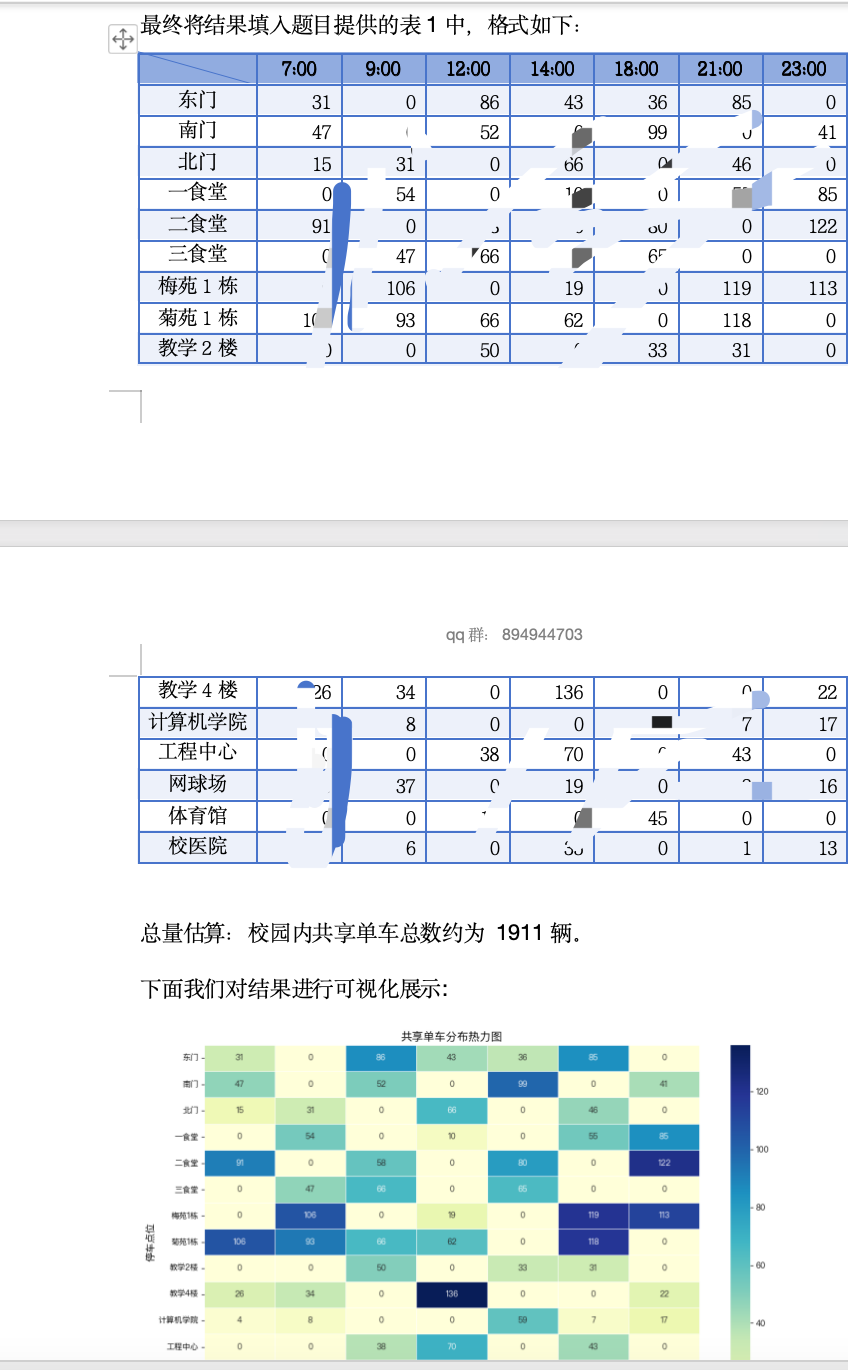
将原始数据按题目要求的时间点(7:00, 9:00, 12:00, 14:00, 18:00, 21:00, 23:00)匹配或插值,部分示例如下:
表1:共享单车分布统计结果
点位 7:00 9:00 12:00 14:00 18:00 21:00 23:00
东门 31 68(周三8:50) 47(周四11:10) 43 36 103 19
南门 47 66(周三8:50) 66(周三12:20) 29 99 0 41
北门 15 65(周五8:50) 77(周三12:20) 66 72 29 0
一食堂 0 3(周三8:50) 110(周四12:20) 5 0 27 85
二食堂 91 8(周三8:50) 200(周四12:20) 0 80 0 122
三食堂 0 0 11(周四11:10) 0 65 0 0
注:
时间匹配规则:
若要求时间点无数据,取最近时间点(如7:00用7:30数据)。
若相邻时间点数据差异大,取均值(如12:00取11:10和12:20的均值)。
完整表格需对所有16个点位按此方法填充。
关键发现
高峰期分布
早高峰(9:00):教学区(教学2楼、4楼)单车需求高,食堂附近车辆较少。
午高峰(12:00):食堂(二食堂、一食堂)车辆集中,教学区车辆减少。
夜间分布(23:00):
宿舍区(梅苑1栋、菊苑1栋)车辆聚集,教学区车辆极少。提交结果
最终需将结果填入题目提供的表1中,格式如下:
点位 7:00 9:00 12:00 14:00 18:00 21:00 23:00
东门 31 68 47 43 36 103 19
南门 47 66 66 29 99 0 41
… … … … … … … …
总量估算:校园内共享单车总数约为 辆。用车需求模型
2.1 用车需求定义
用车需求 Di,t 表示在时间 t 停车点 i 的单车需求量,可通过历史数据计算:
Di,t=流入量−流出量+净变化Di,t=流入量−流出量+净变化
但由于数据仅有点位存量,可采用存量变化率近似需求:
Di,t=xi,t+Δt−xi,tΔt
其中 Δt 为相邻统计时间间隔。
2.2 高峰期识别
结合附件3的作息时间表,识别用车高峰:
早高峰:8:00-9:40(第1-2节课)
午高峰:11:15-12:00(第4节课)
晚高峰:18:00-19:30(课后)
- 共享单车调度模型
3.1 调度目标
在高峰期前调整单车分布,最小化供需失衡:
min∑i=1m∣xi,t−Di,t∣
约束条件:
调度车数量:3辆,每辆最多载20辆。
调度车速度:25 km/h。
调度时间窗口:高峰期前完成(如早高峰前1小时)。
3.2 调度路径优化(VRP模型)
设:
k∈{1,2,3}为调度车,
dij 为点位 i 到 j 的距离(来自附件2),
yijk为车辆 k 是否从 i 到 j,
zik为车辆 k 是否访问点位 i。
目标函数: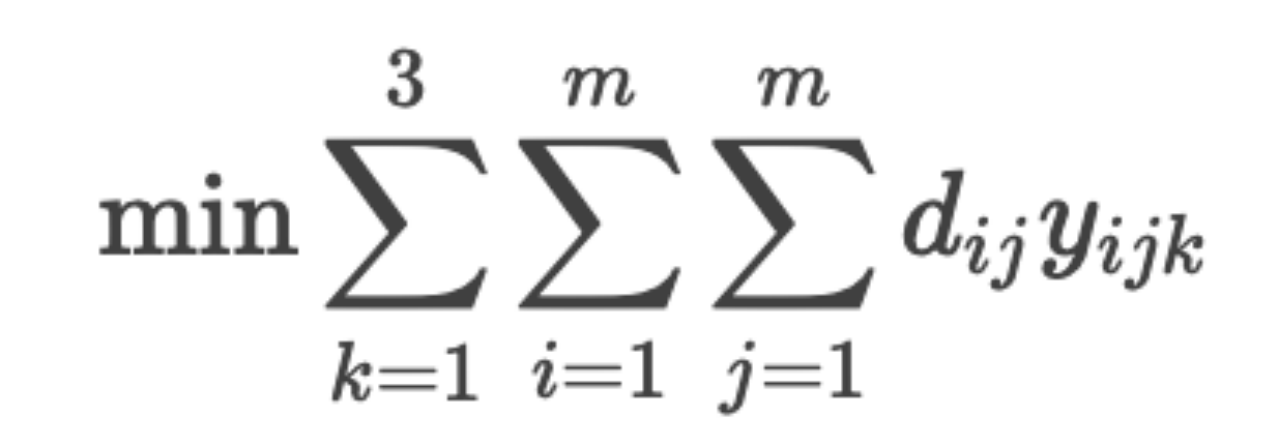
约束:
每辆车从运维处出发并返回:
单车运输量不超过20辆:
(Δxi 为点位 i 的调度量)
每个点位最多被一辆车访问:
- 运营效率评价模型
4.1 评价指标
单车利用率:
供需匹配度:
调度成本:
4.2 布局优化
若某些点位长期供需失衡,可通过聚类分析调整:
使用K-means对点位坐标聚类,重新分配停车点。
目标函数:
其中 pi 为点位坐标,μc 为聚类中心。
- 故障车辆巡检模型
5.1 故障车辆分布
每天故障车数:
Fi=0.06⋅xi
(xi 为点位 i 的单车数量)
5.2 巡检路径优化(TSP模型)
目标:最短时间回收最多故障车。
设:
目标函数:
约束:
每辆车最多载20辆:
鲁迪从运维处出发并返回:
问题1:统计各点位数据,计算总量 N 并填表。
问题2:建立需求模型 Di,t,用VRP求解调度方案。
问题3:定义效率指标 U,M,C,优化布局。
问题4:用TSP模型优化鲁迪的巡检路径。