数据结构-树（2）

一，二叉树

1.1. 二叉树的定义

二叉树是n（n>=0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两颗互不相交的，分别称为根结点的左子树和右子树的二叉树组合。

  如图：

特点：每个结点最多 2 子树，区分左右顺序

1.2. 二叉树的五种形态

• 1.空二叉树
• 2.只有一个根结点
• 3.根结点只有左子树
• 4.根结点只有右子树
• 5.根结点既有左子树又有右子树
• 如图：

1.3. 特殊二叉树

如下思维导图：

• 注意：1.满二叉树一定是一颗完全二叉树，但完全二叉树不一定是满二叉树

1.4. 二叉树的性质

性质一：第 i 层最多 2^(i-1) 个结点（i≥1）

性质二：深度为 k 的二叉树最多 2^k-1 个结点。

性质三：终端结点数 n₀ = 度为 2 的结点数 n₂ + 1（n₀ = n₂ + 1）。终端结点数 n₀ = 度为 2 的结点数 n₂ + 1（n₀ = n₂ + 1）。

性质四：具有n个结点的完全二叉树的深度为【log2^n】+1 （[X]表示不大于x的最大整数）

1.5. 二叉树的存储结构

1.5.1 二叉树顺序存储结构

• 二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，也就是数组的下标要能体现结点之间的逻辑关系，比如双亲与孩子的关系，左右兄弟的关系

• 对于不存在的结点设置为‘^’而已，例如：

1.5.2 二叉链表

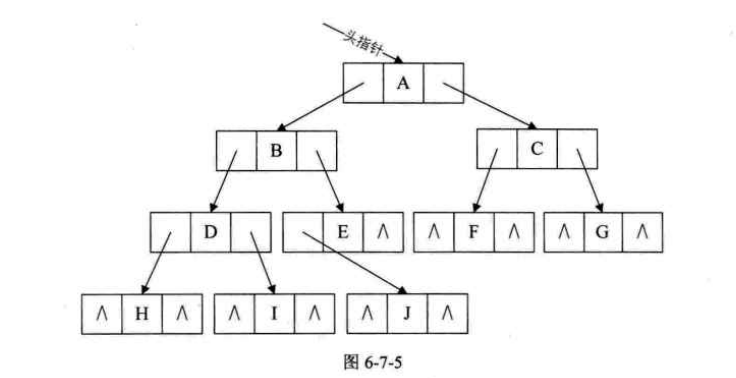
二叉树的每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域是比较自然的想法，我们称这样的链表叫做二叉链表

• 其中data是数据域，lchild和rchild都是指针域，分别存放指向左孩子和右孩子的指针。

以下是我们二叉链表的结点结构定义代码

/*二叉树的二又链表结点结构定义*/
typedefstruct BiTNode /*结点结构
{
TElemType data;/*结点数据*/
struct BiTNode *lchild,*rchild;/*左右孩子指针 */
}BiTNode,*Biree;

 结构如下图：

二，遍历二叉树及其算法

2.1. 二叉树遍历原理

二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次，且仅被访问一次

• 这里的关键词为：访问和次序

2.2. 二叉树的遍历方法

2.2.1. 前序遍历

规则：

若二叉树为空，则空操作返回

否则先访问根结点，然后前序遍历左子树，再前序遍历右子树

遍历顺序为：ABDGHCEIF

2.2.2. 中序遍历

规则：

若二叉树为空，则空操作返回

否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后访问根结点，最后中序遍历右子树

2.2.3. 后序遍历

规则：

若二叉树为空，则空操作返回

否则从左到右先叶子后结点的方式遍历访问左右子树，最后访问根结点

2.2.4. 层序遍历

规则：

若二叉树为空，则空操作返回

否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问

2.3 遍历算法

二叉树的定义是用递归的方式，所有，遍历算法也采用递归

代码示例：

//二叉树结点定义
//#include <stdio.h>
//#include <stdlib.h>
//
 定义二叉树结点结构
//typedef char TElemType;  // 结点数据类型（示例为字符型，可替换为其他类型）
//typedef struct BiTNode {
//    TElemType data;          // 数据域
//    struct BiTNode* lchild;  // 左孩子指针
//    struct BiTNode* rchild;  // 右孩子指针
//} BiTNode, * BiTree;

//前序遍历算法（根→左→右）
/*算法思想：
1.若二叉树为空，直接返回。
2.访问根结点（打印或处理数据）。
3.递归遍历左子树。
4.递归遍历右子树。*/
// 前序遍历递归算法
//void PreOrderTraverse(BiTree T) 
//{
//    if (T == NULL) return;  // 空树返回
//    printf("%c ", T->data);  // 访问根结点（此处为打印，可替换为其他操作）
//    PreOrderTraverse(T->lchild);  // 递归遍历左子树
//    PreOrderTraverse(T->rchild);  // 递归遍历右子树
//}

//中序遍历算法（左→根→右）
/*
算法思想：
若二叉树为空，直接返回。
递归遍历左子树。
访问根结点（打印或处理数据）。
递归遍历右子树。*/
// 中序遍历递归算法
//void InOrderTraverse(BiTree T) {
//    if (T == NULL) return;  // 空树返回
//    InOrderTraverse(T->lchild);  // 递归遍历左子树
//    printf("%c ", T->data);  // 访问根结点
//    InOrderTraverse(T->rchild);  // 递归遍历右子树
//}

//后序遍历算法
/*若二叉树为空，直接返回。
递归遍历左子树。
递归遍历右子树。
访问根结点（打印或处理数据）*/
// 后序遍历递归算法
//void PostOrderTraverse(BiTree T) 
//{
//    if (T == NULL) return;  // 空树返回
//    PostOrderTraverse(T->lchild);  // 递归遍历左子树
//    PostOrderTraverse(T->rchild);  // 递归遍历右子树
//    printf("%c ", T->data);  // 访问根结点
//}

#include <stdio.h>
#include <stdlib.h>

// 定义二叉树结点结构
typedef char TElemType;  // 结点数据类型（示例为字符型，可替换为其他类型）
typedef struct BiTNode {
    TElemType data;          // 数据域
    struct BiTNode* lchild;  // 左孩子指针
    struct BiTNode* rchild;  // 右孩子指针
} BiTNode, * BiTree;

// 函数声明
void CreateBiTree(BiTree* T);
void PreOrderTraverse(BiTree T);
void InOrderTraverse(BiTree T);
void PostOrderTraverse(BiTree T);
void DestroyBiTree(BiTree* T);

// 创建二叉树（按扩展前序序列输入，#表示空结点）
void CreateBiTree(BiTree* T) {
    TElemType ch;
    scanf_s(" %c", &ch);  // 注意空格处理换行符
    if (ch == '#') {
        *T = NULL;
    }
    else {
        *T = (BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data = ch;
        CreateBiTree(&(*T)->lchild);  // 递归创建左子树
        CreateBiTree(&(*T)->rchild);  // 递归创建右子树
    }
}

// 前序遍历递归算法
void PreOrderTraverse(BiTree T) {
    if (T == NULL) return;  // 空树返回
    printf("%c ", T->data);  // 访问根结点
    PreOrderTraverse(T->lchild);  // 递归遍历左子树
    PreOrderTraverse(T->rchild);  // 递归遍历右子树
}

// 中序遍历递归算法
void InOrderTraverse(BiTree T) {
    if (T == NULL) return;  // 空树返回
    InOrderTraverse(T->lchild);  // 递归遍历左子树
    printf("%c ", T->data);  // 访问根结点
    InOrderTraverse(T->rchild);  // 递归遍历右子树
}

// 后序遍历递归算法
void PostOrderTraverse(BiTree T) {
    if (T == NULL) return;  // 空树返回
    PostOrderTraverse(T->lchild);  // 递归遍历左子树
    PostOrderTraverse(T->rchild);  // 递归遍历右子树
    printf("%c ", T->data);  // 访问根结点
}

// 释放二叉树内存
void DestroyBiTree(BiTree* T) {
    if (*T != NULL) {
        DestroyBiTree(&(*T)->lchild);  // 递归释放左子树
        DestroyBiTree(&(*T)->rchild);  // 递归释放右子树
        free(*T);  // 释放当前结点
        *T = NULL;  // 防止野指针
    }
}

int main() {
    BiTree T = NULL;
    printf("输入扩展前序序列（#表示空结点）: ");
    CreateBiTree(&T);  // 例如输入：AB#D##C##（对应书中示例树）

    printf("\n前序遍历结果: ");
    PreOrderTraverse(T);

    printf("\n中序遍历结果: ");
    InOrderTraverse(T);

    printf("\n后序遍历结果: ");
    PostOrderTraverse(T);

    // 释放内存
    DestroyBiTree(&T);
    printf("\n二叉树内存已释放\n");

    return 0;
}

三，线索二叉树

1.定义：指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应地二叉树就称为线索二叉树

由于这样，我们分不清lchild是指向前继还是左孩子，rchild是指向后继还是右孩子

故我们增加新的两个标志域ltag和rtag，用来存放布尔型变量。如下图：

2.线索二叉树结构实现

#include <stdio.h>
#include <stdlib.h>

// 定义线索二叉树结点结构
typedef char TElemType;
typedef struct BiThrNode {
    TElemType data;                // 数据域
    struct BiThrNode* lchild, * rchild; // 左右指针
    int ltag, rtag;                // 左右标志（0:孩子，1:线索）
} BiThrNode, * BiThrTree;

BiThrTree pre = NULL; // 全局前驱结点指针

// 创建普通二叉树（按扩展前序序列输入，#表示空结点）
void CreateBiTree(BiThrTree* T) {
    TElemType ch;
    scanf_s(" %c", &ch);  // 注意空格处理前导空白
    if (ch == '#') {
        *T = NULL;
    }
    else {
        *T = (BiThrNode*)malloc(sizeof(BiThrNode));
        (*T)->data = ch;
        (*T)->ltag = 0;  // 初始默认指向孩子
        (*T)->rtag = 0;
        CreateBiTree(&(*T)->lchild);  // 递归创建左子树
        CreateBiTree(&(*T)->rchild);  // 递归创建右子树
    }
}

// 中序线索化二叉树（递归函数）
void InThreading(BiThrTree T) {
    if (T) {
        InThreading(T->lchild);  // 递归线索化左子树

        // 处理当前结点的前驱线索
        if (!T->lchild) {
            T->ltag = 1;
            T->lchild = pre;
        }
        // 处理前驱结点的后继线索
        if (pre && !pre->rchild) {
            pre->rtag = 1;
            pre->rchild = T;
        }
        pre = T;  // 更新前驱结点

        InThreading(T->rchild);  // 递归线索化右子树
    }
}

// 创建中序线索二叉树（调用入口）
BiThrTree CreateInThreadedBiTree() {
    BiThrTree T, head;
    // 创建头结点
    head = (BiThrNode*)malloc(sizeof(BiThrNode));
    head->ltag = 0;  // lchild指向根结点
    head->rtag = 1;  // rchild指向遍历的最后一个结点
    head->rchild = head;  // 初始时指向自己

    printf("请输入扩展前序序列（#表示空结点）: ");
    CreateBiTree(&T);  // 创建普通二叉树

    if (!T) {  // 空树处理
        head->lchild = head;
    }
    else {
        head->lchild = T;  // 头结点lchild指向根
        pre = head;
        InThreading(T);  // 中序线索化

        // 处理最后一个结点
        pre->rchild = head;  // 修正：添加缺失的分号
        pre->rtag = 1;       // 修正：添加缺失的分号
        head->rchild = pre;  // 头结点的rchild指向中序遍历的最后一个结点
    }
    return head;
}

// 中序遍历线索二叉树（非递归）
void InOrderTraverse_Thr(BiThrTree T) {
    BiThrTree p = T->lchild;  // p指向根结点
    while (p != T) {  // 循环直到回到头结点
        // 找到最左结点（中序遍历的第一个结点）
        while (p->ltag == 0) {
            p = p->lchild;
        }
        printf("%c ", p->data);  // 访问结点

        // 沿后继线索访问后续结点
        while (p->rtag == 1 && p->rchild != T) {
            p = p->rchild;
            printf("%c ", p->data);
        }
        p = p->rchild;  // 转向右子树
    }
}

// 释放线索二叉树的内存
void DestroyBiTree(BiThrTree* T) {
    if (*T && (*T)->ltag == 0) {  // 如果不是头结点且有左孩子
        DestroyBiTree(&(*T)->lchild);  // 递归释放左子树
    }
    if (*T && (*T)->rtag == 0) {  // 如果不是头结点且有右孩子
        DestroyBiTree(&(*T)->rchild);  // 递归释放右子树
    }
    free(*T);  // 释放当前结点
    *T = NULL;
}

int main() {
    BiThrTree T;

    T = CreateInThreadedBiTree();  // 创建中序线索二叉树

    printf("\n中序遍历线索二叉树结果: ");
    InOrderTraverse_Thr(T);  // 中序遍历线索二叉树

    DestroyBiTree(&T);  // 释放内存
    printf("\n二叉树内存已释放。\n");

    return 0;
}

四，赫尔曼树及其应用

1.原理

1. 基本概念
   赫尔曼树（Huffman Tree）是一种最优二叉树，其核心目标是最小化带权路径长度（WPL）。带权路径长度定义为所有叶子节点的权值（如字符频率）与其到根节点路径长度的乘积之和。

2. 构建步骤

   • 初始化：将每个字符视为一个节点，权值为其频率，构成森林。

   • 贪心合并：重复选择权值最小的两个节点，合并为新节点（权值为二者之和），直到只剩一棵树。

   • 生成结构：最终形成的树中，权值高的节点靠近根，权值低的远离根。

3. 特性

   • 最优性：生成的树具有最小的带权路径长度。

   • 前缀编码：字符编码唯一且无歧义（任一编码不是另一编码的前缀）。

   • 不唯一性：相同权值节点合并顺序不同可能导致不同树结构，但WPL相同。

2.应用

1. 数据压缩

   • 哈夫曼编码：将高频字符用短编码表示，低频字符用长编码，显著减少存储空间（如ZIP、GIF、JPEG等格式）。

   • 文本压缩：适用于重复性高的文本文件，压缩效率高且无损。

2. 通信传输

   • 编码优化：在网络协议或通信中减少数据传输量（如HTTP/2的头部压缩）。

   • 实时传输：结合动态哈夫曼编码适应数据流变化（需频率统计更新）。

3. 文件系统

   • 存储优化：在文件系统中压缩重复数据，提升存储利用率。

4. 其他领域

   • 图像/音频压缩：如PNG（图像）、MP3（音频）的部分压缩阶段。

   • 决策树设计：在机器学习中构建高效分类路径。

3.优缺点

• 优点：编码效率高、实现简单、适用于静态数据。

• 缺点：需预先统计频率（静态编码），动态数据需额外处理（如自适应哈夫曼编码）。

代码示例：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>

typedef struct HTNode {
    int weight;
    int parent, lchild, rchild;
} HTNode, * HuffmanTree;

typedef char** HuffmanCode;

void Select(HuffmanTree HT, int n, int* s1, int* s2) {
    int min1 = INT_MAX, min2 = INT_MAX;
    *s1 = *s2 = 0;

    // 寻找第一个最小值
    for (int i = 1; i <= n; ++i) {
        if (HT[i].parent == 0 && HT[i].weight < min1) {
            min1 = HT[i].weight;
            *s1 = i;
        }
    }

    // 寻找第二个最小值（排除已选节点）
    for (int i = 1; i <= n; ++i) {
        if (HT[i].parent == 0 && i != *s1 && HT[i].weight < min2) {
            min2 = HT[i].weight;
            *s2 = i;
        }
    }
}

void CreateHuffmanTree(HuffmanTree* HT, int* w, int n) {
    if (n <= 1) return;

    int m = 2 * n - 1;
    *HT = (HuffmanTree)malloc((m + 1) * sizeof(HTNode));

    // 初始化叶子节点
    for (int i = 1; i <= n; ++i) {
        (*HT)[i].weight = w[i - 1];
        (*HT)[i].parent = 0;
        (*HT)[i].lchild = 0;
        (*HT)[i].rchild = 0;
    }
    // 初始化非叶子节点
    for (int i = n + 1; i <= m; ++i) {
        (*HT)[i].weight = 0;
        (*HT)[i].parent = 0;
        (*HT)[i].lchild = 0;
        (*HT)[i].rchild = 0;
    }

    // 构建树
    for (int i = n + 1; i <= m; ++i) {
        int s1, s2;
        Select(*HT, i - 1, &s1, &s2);
        (*HT)[s1].parent = i;
        (*HT)[s2].parent = i;
        (*HT)[i].lchild = s1;
        (*HT)[i].rchild = s2;
        (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
    }
}

void CreateHuffmanCode(HuffmanTree HT, HuffmanCode* HC, int n) {
    *HC = (HuffmanCode)malloc((n + 1) * sizeof(char*));
    char* cd = (char*)malloc(n * sizeof(char));
    cd[n - 1] = '\0';

    for (int i = 1; i <= n; ++i) {
        int start = n - 1;
        for (int c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent) {
            cd[--start] = (HT[f].lchild == c) ? '0' : '1';
        }
        (*HC)[i] = (char*)malloc((n - start) * sizeof(char));
        strcpy_s((*HC)[i],n-start, &cd[start]); // 改用标准strcpy
    }
    free(cd);
}

int WPL(HuffmanTree HT, int n) {
    int wpl = 0;
    for (int i = 1; i <= n; ++i) {
        int depth = 0;
        for (int c = i; HT[c].parent != 0; c = HT[c].parent, ++depth);
        wpl += HT[i].weight * depth;
    }
    return wpl;
}

void Decode(HuffmanTree HT, char* code, int root, char* result) {
    int p = root, index = 0;
    size_t len = strlen(code);

    for (size_t i = 0; i < len; ++i) {
        p = (code[i] == '0') ? HT[p].lchild : HT[p].rchild;

        // 检查节点有效性
        if (p < 1 || p > root) {
            fprintf(stderr, "Invalid code at position %zu\n", i);
            result[0] = '\0';
            return;
        }

        if (HT[p].lchild == 0 && HT[p].rchild == 0) {
            result[index++] = 'A' + (p - 1);
            p = root; // 重置到根节点继续解码
        }
    }
    result[index] = '\0';
}

void PrintHuffmanTree(HuffmanTree HT, int m) {
    printf("\nHuffman Tree Structure (index starts from 1):\n");
    printf("Index\tWeight\tParent\tLeft\tRight\n");
    for (int i = 1; i <= m; ++i) {
        printf("%d\t%d\t%d\t%d\t%d\n",
            i, HT[i].weight, HT[i].parent, HT[i].lchild, HT[i].rchild);
    }
}

int main() {
    int w[] = { 5, 9, 12, 13, 16 };
    int n = sizeof(w) / sizeof(w[0]);

    HuffmanTree HT;
    HuffmanCode HC;

    CreateHuffmanTree(&HT, w, n);
    PrintHuffmanTree(HT, 2 * n - 1);

    CreateHuffmanCode(HT, &HC, n);
    printf("\nHuffman Codes:\n");
    for (int i = 1; i <= n; ++i) {
        printf("Char %c: %s\n", 'A' + i - 1, HC[i]);
    }

    printf("\nWPL = %d\n", WPL(HT, n));

    char code[] = "0110";
    char result[100];
    Decode(HT, code, 2 * n - 1, result);
    printf("\nDecode '%s' => %s\n", code, result);

    // 释放内存
    for (int i = 1; i <= n; ++i) free(HC[i]);
    free(HC);
    free(HT);

    return 0;
}