一、树
1.树的概念
之前我们一直在谈的是一对一的线性结构,现实中,还存在很多一对多的情况需要处理,一对多的线性结构——树。


树的结点包括一个数据元素及若干指向其子树的分支,结点拥有的子树数称为结点的度。度为0的结点称为叶结点或者终端结点;度不为0的结点称为非终端结点或者分支节点。除根节点外,分支节点也称为内部节点树的度是树内各节点的度的最大值。

结点的关系:结点的子树的根称为该结点的孩子,相应地,该结点称为孩子的双亲。
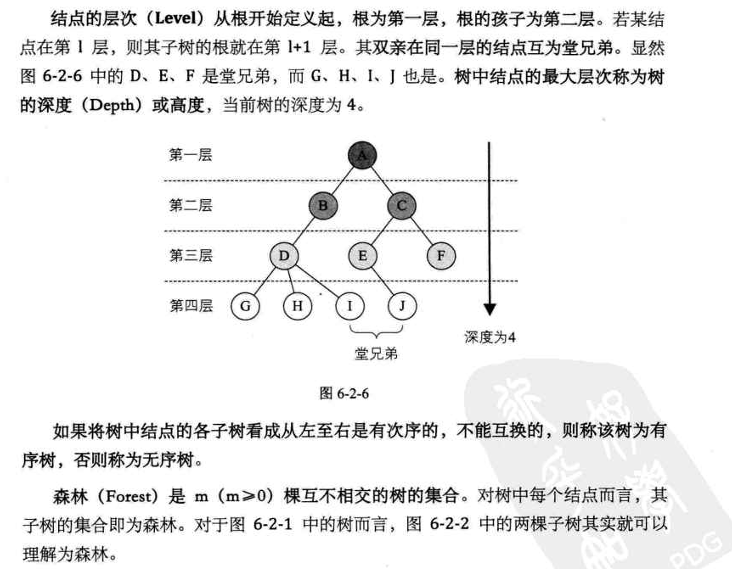
结点的层次:
2. 二叉树

二叉树的特点:
3. 特殊二叉树
- 斜树
- 满二叉树
- 完全二叉树
4. 树的存储结构
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域,我们称这样的链表叫做二叉链表:
![]()
其中data是数据域,Ichild和rchild都是指针域,分别存放指向左孩子和右孩子的指针。
5.树的基本操作
- 树的结构定义
typedef char DATATYPE; // 定义树节点存储的数据类型为字符
typedef struct _tree_node_
{
DATATYPE data; // 节点存储的数据
struct _tree_node_ *left, *right; // 左右子树指针
} TreeNode; // 二叉树节点结构
// 创建二叉树(双星指针用于修改外部指针的值)
char data[]="abd#f###c#eg###"; // 带空节点标记的先序遍历序列
int ind = 0; // 全局索引,用于遍历数据数组
- 创建树
void CreateTree(TreeNode** root)
{
char c = data[ind++]; // 读取当前字符并移动索引
if('#' == c) // '#'表示空节点
{
*root = NULL; // 当前节点置空
return;
}
else
{
*root = malloc(sizeof(TreeNode)); // 创建新节点
if(NULL == *root)
{
fprintf(stderr, "CreateTree malloc error");
return;
}
(*root)->data = c; // 设置节点数据
CreateTree(&(*root)->left); // 递归创建左子树
CreateTree(&(*root)->right); // 递归创建右子树
}
}- 树的三种遍历方式
// 前序遍历(根-左-右)
void PreOrderTraverse(TreeNode* root)
{
if(NULL == root) // 空节点直接返回
{
return;
}
printf("%c", root->data); // 访问根节点
PreOrderTraverse(root->left); // 递归遍历左子树
PreOrderTraverse(root->right); // 递归遍历右子树
}
// 中序遍历(左-根-右)
void InOrderTraverse(TreeNode* root)
{
if (root == NULL) return;
InOrderTraverse(root->left);
printf("%c", root->data);
InOrderTraverse(root->right);
}
// 后序遍历(左-右-根)
void PostOrderTraverse(TreeNode* root)
{
if (root == NULL) return;
PostOrderTraverse(root->left);
PostOrderTraverse(root->right);
printf("%c", root->data);
}
- 树的销毁
void DestroyTree(TreeNode* root)
{
if (root == NULL)
{
return;
}
DestroyTree(root->left);
DestroyTree(root->right);
free(root);
}二、哈希表

关键逻辑说明(除留取余法):
哈希函数与冲突处理:
- 使用简单的取模运算作为哈希函数,可能导致较多冲突(如 12 和 24 对 12 取模均为 0)。
- 采用线性探测法处理冲突:当槽位被占时,依次尝试下一个槽位(
ind = (ind + 1) % tlen)。插入流程:
- 插入数据时,若遇到冲突(槽位非 - 1),持续探测直到找到空槽位(值为 - 1)。
- 示例中输出冲突信息,可观察线性探测过程(如 67%12=7,若槽位 7 被占,尝试 8、9...)。
查找流程:
- 从初始哈希值开始探测,若未找到则按顺序查找下一个槽位。
- 通过记录初始索引
old_ind,避免在满表时陷入无限循环。内存管理:
- 示例中未释放哈希表内存,实际使用中需在程序结束前调用
free释放hs->head和hs,避免内存泄漏。示例输出与分析
假设插入数据
array时的冲突过程如下(以 12 和 67 为例):
- 12%12=0:槽位 0 为空,直接插入。
- 67%12=7:槽位 7 为空,直接插入。
- 56%12=8:槽位 8 为空,直接插入。
- 16%12=4:槽位 4 为空,直接插入。
- 25%12=1:槽位 1 为空,直接插入。
- 37%12=1:槽位 1 已被 25 占用,探测 2→空,插入槽位 2。
- ...(其他数据类似,可能产生多次冲突)
查找 37 时,计算哈希值 1→探测 2,找到数据,返回槽位 2。
#include <stdio.h> // 标准输入输出
#include <stdlib.h> // 内存分配函数(malloc/free)
#include <string.h> // 字符串处理(此处未用到,但保留可能的扩展需求)
// 定义数据类型别名(当前为整数,可修改为其他类型)
typedef int DATATYPE;
// 哈希表结构体定义
typedef struct {
DATATYPE* head; /**< 指向哈希表数组的指针,存储数据 */
int tlen; /**< 哈希表的长度(数组大小) */
} HSTable;
/**
* @brief 创建哈希表并初始化
* @param len 哈希表的长度(数组大小)
* @return HSTable* 指向新创建的哈希表的指针,失败时返回NULL
* @note 哈希表数组元素初始化为-1(假设-1表示空槽位)
*/
HSTable* CreateHsTable(int len) {
// 1. 分配哈希表结构体内存
HSTable* hs = malloc(sizeof(HSTable));
if (NULL == hs) {
// 内存分配失败,输出错误信息到标准错误流
fprintf(stderr, "CreateHsTable: 分配结构体内存失败\n");
return NULL;
}
// 2. 分配哈希表数据数组内存
hs->head = malloc(sizeof(DATATYPE) * len);
if (NULL == hs->head) {
// 数据数组分配失败,释放已分配的结构体内存
fprintf(stderr, "CreateHsTable: 分配数据数组内存失败\n");
free(hs); // 避免内存泄漏
return NULL;
}
// 3. 初始化哈希表数组:所有槽位标记为-1(空)
hs->tlen = len;
int i = 0;
for (i = 0; i < len; i++) {
hs->head[i] = -1;
}
return hs;
}
/**
* @brief 哈希函数:计算数据的哈希值(取模运算)
* @param hs 哈希表指针(用于获取表长度)
* @param data 待计算的数据源指针
* @return int 哈希值(即数组索引)
* @note 直接使用数据值对表长取模,简单但可能导致较多冲突
*/
int HSFun(HSTable* hs, DATATYPE* data) {
return *data % hs->tlen; // 例如:数据12对12取模得到0
}
/**
* @brief 向哈希表中插入数据(开放寻址法处理冲突,线性探测)
* @param hs 哈希表指针
* @param data 待插入的数据指针
* @return int 0表示成功,其他值可扩展为错误码
* @note 当槽位被占用时,逐个探测下一个槽位(线性探测)
*/
int HSInsert(HSTable* hs, DATATYPE* data) {
// 1. 计算初始哈希值
int ind = HSFun(hs, data);
// 2. 线性探测寻找空槽位
while (hs->head[ind] != -1) {
// 输出冲突信息(调试用)
printf("冲突:位置 %d 已被占用,数据 %d 尝试下一个位置\n", ind, *data);
// 移动到下一个槽位(取模实现循环探测)
ind = (ind + 1) % hs->tlen;
}
// 3. 插入数据到空槽位
hs->head[ind] = *data;
return 0;
}
/**
* @brief 在哈希表中查找数据
* @param hs 哈希表指针
* @param data 待查找的数据指针
* @return int 找到时返回数据所在槽位索引,-1表示未找到
* @note 使用线性探测法遍历可能的槽位,避免陷入死循环
*/
int HsSearch(HSTable* hs, DATATYPE* data) {
// 1. 计算初始哈希值
int ind = HSFun(hs, data);
// 记录初始索引,用于判断是否绕表一周(避免死循环)
int old_ind = ind;
// 2. 线性探测查找数据
while (hs->head[ind] != *data) {
// 移动到下一个槽位
ind = (ind + 1) % hs->tlen;
// 若回到初始索引,说明未找到
if (old_ind == ind) {
return -1;
}
}
return ind; // 返回找到的槽位索引
}
int main(int argc, char** argv) {
// 1. 创建长度为12的哈希表
HSTable* hs = CreateHsTable(12);
if (hs == NULL) {
return 1; // 创建失败,退出程序
}
// 2. 测试数据数组
int array[] = {12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34};
int i = 0;
int array_len = sizeof(array) / sizeof(array[0]); // 计算数组长度(12)
// 3. 插入数据到哈希表
for (i = 0; i < array_len; i++) {
HSInsert(hs, &array[i]);
}
// 4. 查找数据37
int want_num = 37;
int ret = HsSearch(hs, &want_num);
// 5. 输出查找结果
if (-1 == ret) {
printf("未找到数据 %d\n", want_num);
} else {
printf("找到数据 %d,位于槽位 %d\n", hs->head[ret], ret);
}
// 6. 释放哈希表内存(示例中未实现,实际需添加)
// free(hs->head);
// free(hs);
return 0;
}三、内核链表
1、Linux内核链表是一种数据结构,它在Linux内核编程中广泛使用,用于管理各种类
型的数据元素。链表由一系列节点组成,每个节点包含指向下一个节点和前一个节点的
指针。这种设计使得链表在插入和删除操作时非常高效,因为不需要移动其他元素。
2、链表的定义和初始化
(1)在Linux内核中,链表通过包含list_head结构体的方式在各种数据结构中实现。
(2)list_head结构体定义在<linux/list.h>头文件中,包含next和prev两个指针,分别指
向链表的下一个和前一个元素。要使用内核链表,首先需要包含这个头文件。
(3)初始化链表时,可以使用INIT_LIST_HEAD宏,它将链表的next和prev指针都指向
链表本身,形成一个循环链表。
内核链表是双向循环链表:

注:内部增删改查已经写好,将需要的内容组合到结构体中即可使用
(可通过www.kernel.org去下载内核)
3、内核链表的思想:普通链表与数据耦合性高,自己定义结构体,将数据放入;
(1)offset宏:传入结构体,成员,通过宏进入,计算node的偏移量是多少;
(2)contrainof宏:返回该类型指针的地址。
4、内核链表提供了一系列宏和函数来进行操作,如添加、删除和遍历节点:
(1)添加节点:使用list_add或list_add_tail函数可以在链表的头部或尾部添加新节点。
(2)删除节点:使用list_del函数可以从链表中删除节点。
(3)遍历链表:使用list_for_each或list_for_each_entry宏可以遍历链表中的每个元素。
5、注意事项在:使用内核链表时,需要注意几个重要的点:
(1)内存管理:当添加新节点到链表时,需要确保为节点分配了内存。同样,从链表
中删除节点时,需要释放节点占用的内存。
(2)同步:在多线程环境中操作链表时,可能需要使用锁来避免竞态条件。
(3)性能:虽然链表在插入和删除操作时非常高效,但在查找元素时可能需要遍历整
个链表,这可能会影响性能。