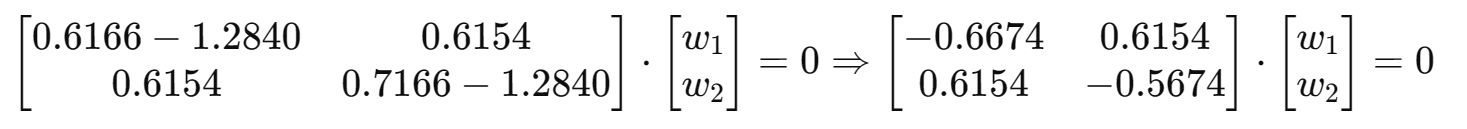目录
一、基本概念
主成分分析(PCA)是一种经典的降维技术,广泛应用于机器学习和数据分析中。其核心目标是通过线性变换将高维数据投影到低维空间,同时尽可能保留数据的方差(即信息量)。PCA通过找到一组新的正交基(称为主成分),使数据在这些基上的投影具有最大方差,从而实现降维。
- 降维的目的:高维数据通常包含冗余信息或噪声,PCA通过保留主要信息(高方差方向)来减少维度,降低计算复杂度和过拟合风险。
- 正交性:主成分之间是正交的,确保降维后的特征不相关。
- 方差最大化:主成分的方向是数据协方差矩阵的特征向量,对应的特征值表示该方向的方差大小。
二、数学推导
2.1 问题设定:寻炸最大方差的投影方向
假定有n个样本,每个样本是d维的特征向量,记为

目标:找一个单位向量 w,使得所有样本在 w 上的投影后的方差
2.2 数据中心化
将数据零均值化:

处理后的数据矩阵 X 是 维的,每行是一个样本,且均值为0
2.3 目标函数:最大化投影后的方差
将样本 投影到方向 w上:

投影后的所有样本为向量
目标是最大化 Z 的方差:
设协方差矩阵:
所以目标函数变为:最大化
2.4 约束条件
约束w为单位向量![]()
2.5 拉格朗日乘子法
构造拉格朗日函数

对w求导并令其为0
2.6 主成分提取
是对称正定矩阵,因此存在d个正交的特征向量
,以及对应的特征值
- 第一主成分:
(最大方差方向)
- 第二主成分:
,且与
正交
- 以此类推
2.7 降维公式
将前 k个特征向量组成投影矩阵 ,原始样本 X 的降维结果为:

实际案例演示
有如下2D数据集(每一行是一个样本,两个特征
,
):
(1)数据中心化(零均值)
计算均值
:
每个样本减去均值:
(2)计算协方差矩阵
(3)求协方差矩阵的特征值和特征向量
求
的特征值与特征向量:
【具体求解过程】
①求特征值(解特征方程)
的特征值
,满足:
即有:
行列式展开:
解方程得:
②求特征向量
对于每个特征值
,解线性方程组:
以
为例:
解方程组可得:
(4)投影数据到主成分轴
只保留第一主成分
,则降维后(1D)的结果为:
例如第一个样本:
三、SVD
SVD 全称为 Singular Value Decomposition,即奇异值分解,是矩阵分解的一种形式:
对于任意的实矩阵,都可以分解为:

是列正交矩阵,即
是对角矩阵,对角线上的值就是奇异值(从大到小排列)
是行正交矩阵,即
SVD 与 PCA 的关系
- PCA 本质上就是对协方差矩阵做特征分解
- 而协方差矩阵
,其特征分解其实就等价于对 X 做SVD:
因此
- V的列就是PCA的主成分方向(特征向量)
的对角线元素就是协方差矩阵的特征值
四、实际案例分析
本实验使用 ORL Faces 人脸数据集,通过手动实现的主成分分析(PCA)算法对高维人脸图像数据进行降维处理。代码通过 Python 实现,加载 ORL Faces 数据集(包含 40 个类别的灰度人脸图片,每类约 10 张,格式为 .pgm),执行 PCA 降维,保留前 50 个主成分,并可视化降维后的数据分布以及原始图片与重建图片的对比。实验路径为 D:/Desktop/Code/ML/ML/PCA/ORL_Faces/ORL_Faces,假设图片尺寸为 112×92 112 \times 92 112×92,展平后每张图片为 10,304 维向量。
主要步骤包括:
- 数据加载:读取 ORL Faces 数据集中的 .pgm 图片,展平为一维向量,构建数据矩阵 X X X(形状 N×D N \times D N×D,其中 N≈400 N \approx 400 N≈400,D=112×92=10,304 D = 112 \times 92 = 10,304 D=112×92=10,304)。
- 数据标准化:对数据进行零均值、单位方差标准化。
- 手动 PCA:
- 计算协方差矩阵并进行特征值分解。
- 选择前 50 个主成分(特征向量),投影数据到低维空间。
- 计算解释方差比,评估降维效果。
- 可视化:
- 绘制前两个主成分的散点图,展示数据在低维空间的分布。
- 随机选择 5 张图片,比较原始图片与 PCA 重建图片的视觉效果。
- 数据保存:将降维后的数据保存为 X_pca_manual.npy。
实验代码:
import numpy as np
import os
from PIL import Image
import matplotlib.pyplot as plt
# 1. 加载ORL_Faces数据集
def load_images(base_path):
data = []
labels = []
image_paths = [] # 保存图片路径以便后续显示
if not os.path.exists(base_path):
raise FileNotFoundError(f"数据集目录不存在: {base_path}")
print(f"正在查找数据集: {base_path}")
for i in range(1, 41): # s1 to s40
folder = os.path.join(base_path, f's{i}')
if not os.path.exists(folder):
print(f"警告: 子文件夹不存在,跳过: {folder}")
continue
print(f"正在处理文件夹: {folder}")
for filename in os.listdir(folder):
if filename.endswith('.pgm'):
img_path = os.path.join(folder, filename)
try:
img = Image.open(img_path).convert('L') # 转换为灰度图
img_array = np.array(img).flatten() # 展平为一维向量
data.append(img_array)
labels.append(i) # 记录类别
image_paths.append(img_path) # 记录图片路径
except Exception as e:
print(f"加载图片 {img_path} 出错: {e}")
if not data:
raise ValueError("未找到任何有效的 .pgm 图片。")
return np.array(data), np.array(labels), image_paths
# 2. 手动实现PCA
def manual_pca(X, n_components):
# 标准化数据
X_mean = np.mean(X, axis=0)
X_std = np.std(X, axis=0)
X_std_data = (X - X_mean) / X_std
# 计算协方差矩阵
cov_matrix = np.cov(X_std_data.T)
# 特征值分解
eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)
# 按特征值从大到小排序
idx = np.argsort(eigenvalues)[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
# 计算解释方差比
explained_variance_ratio = eigenvalues / np.sum(eigenvalues)
print(f"解释方差比: {np.sum(explained_variance_ratio[:n_components]):.4f}")
# 选择前n_components个特征向量
selected_vectors = eigenvectors[:, :n_components]
# 投影到主成分空间
X_pca = np.dot(X_std_data, selected_vectors)
# 返回重建所需的数据
return X_pca, selected_vectors, X_mean, X_std, explained_variance_ratio
# 3. 可视化原始和重建图片
def visualize_reconstruction(original_data, reconstructed_data, image_paths, img_shape, num_samples=5):
# 随机选择 num_samples 张图片
indices = np.random.choice(original_data.shape[0], num_samples, replace=False)
# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 创建子图
fig, axes = plt.subplots(num_samples, 2, figsize=(8, num_samples * 4))
if num_samples == 1:
axes = [axes] # 确保单张图片时 axes 可迭代
for i, idx in enumerate(indices):
# 原始图片
original_img = original_data[idx].reshape(img_shape)
axes[i, 0].imshow(original_img, cmap='gray')
axes[i, 0].set_title(f'原始图片 (ID: {idx})')
axes[i, 0].axis('off')
# 重建图片
reconstructed_img = reconstructed_data[idx].reshape(img_shape)
axes[i, 1].imshow(reconstructed_img, cmap='gray')
axes[i, 1].set_title(f'PCA 重建图片 (ID: {idx})')
axes[i, 1].axis('off')
plt.suptitle('原始图片与 PCA 重建图片对比')
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
# 4. 主程序
def main():
# 数据集路径
base_path = 'D:/Desktop/Code/ML/ML/PCA/ORL_Faces/ORL_Faces' # 请确认实际路径
try:
X, y, image_paths = load_images(base_path)
except Exception as e:
print(f"加载图片失败: {e}")
return
# 保存原始数据和图片尺寸
X_original = X.copy()
img_shape = (112, 92) # ORL Faces 图片尺寸,通常为 112x92
# 应用手动PCA
n_components = 50 # 降维后的维度
X_pca, selected_vectors, X_mean, X_std, explained_variance = manual_pca(X, n_components)
# 重建数据
X_reconstructed = np.dot(X_pca, selected_vectors.T) # 逆投影
X_reconstructed = X_reconstructed * X_std + X_mean # 恢复标准化前的尺度
# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 可视化前两个主成分
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.xlabel('第一个主成分')
plt.ylabel('第二个主成分')
plt.title('ORL Faces 数据集的手动 PCA 结果')
plt.colorbar(label='类别')
plt.show()
# 可视化原始和重建图片
visualize_reconstruction(X_original, X_reconstructed, image_paths, img_shape, num_samples=5)
# 保存降维后的数据
np.save('X_pca_manual.npy', X_pca)
if __name__ == '__main__':
main()实验结果: