
演示基于PaddlePaddle自动求导技术实现梯度下降,简化求解过程。
01、梯度下降法
梯度下降法是机器学习领域非常重要和具有代表性的算法,它通过迭代计算来逐步寻找目标函数极小值。既然是一种迭代计算方法,那么最重要的就是往哪个方向迭代,梯度下降法选择从目标函数的梯度切入。首先需要明确一个数学概念,即函数的梯度方向是函数值变化最快的方向。梯度下降法就是基于此来进行迭代。
图2.28对应一个双自变量函数
![]()
。想要求得该函数极小值,只需要随机选择一个初始点,然后计算当前点对应的梯度,按照梯度反方向下降一定高度,然后重新计算当前位置对应的梯度,继续按照梯度反方向下降。按照上述方式迭代,最终就可以用最快的速度到达极小值附近。
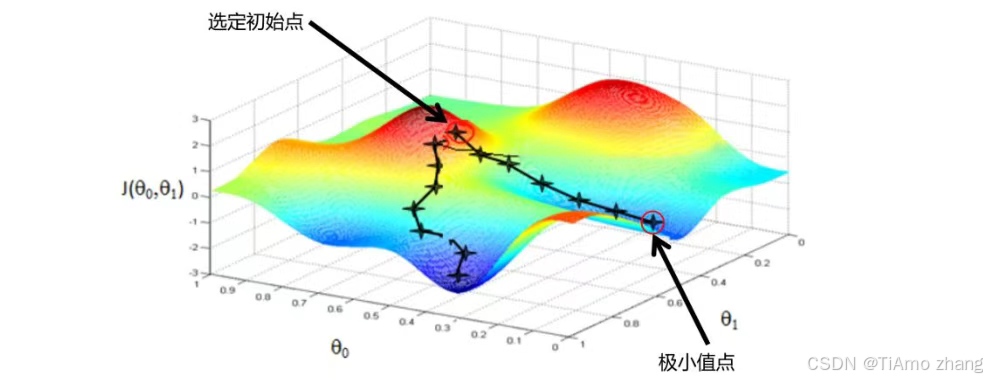
如果函数很复杂并有多个极小值点,那么选择不同的初始值,按照梯度下降算法的计算方式很有可能会到达不同的极小值点,并且耗时也不一样。因此,在工程实现上选择一个好的初始值是非常重要的。
对于前面的直线拟合任务来说,其目标函数就是L,模型参数就是a和b。按照梯度下降算法的原理,对应实现步骤如下:
(1)初始化模型参数a和b;
(2)输入每个样本x,根据公式y=ax+b计算每个样本数据的预测输出值
![]()
;
(3)计算所有样本的预测值
![]()
和真值y之间的平方差L;
(4)计算当前L对模型参数a和b的梯度值,即
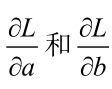
;
按照下式更新参数a和b:
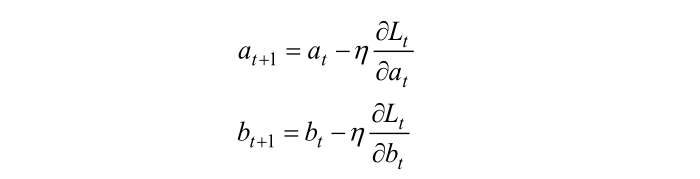
其中t表示当前迭代的轮次,
![]()
是一个提前设置好的参数,这个参数的作用是代表每一步迭代下降的跨度,专业术语也叫学习率;
(6)重复步骤(2)~(5),直至迭代次数超过某个预设值。
注意到,上述算法第(5)步中,需要计算目标函数L对a和b的偏导。尽管对于这个直线拟合任务来说其偏导求取非常简单,但是依然需要手工进行求导。在2.3.3节中,介绍过可以通过PaddlePaddle来自动计算梯度,因此,可以使用PaddlePaddle来更便捷的实现这个梯度下降算法。
完整代码如下(machine_learning/auto_diff.py):
import matplotlib.pyplot as plt
import numpy as np
import paddle
# 输入数据
x_train = np.array( [3.3, 4.4, 5.5, 6.7, 6.9, 4.2, 9.8, 6.2, 7.6, 2.2, 7, 10.8, 5.3, 8, 3.1], dtype=np.float32,)
y_train = np.array( [17, 28, 21, 32, 17, 16, 34, 26, 25, 12, 28, 35, 17, 29, 13], dtype=np.float32)
# numpy转tensor
x_train = paddle.to_tensor(x_train)
y_train = paddle.to_tensor(y_train)
# 随机初始化模型参数
a = np.random.randn(1)
a = paddle.to_tensor(a, dtype="float32", stop_gradient=False)
b = np.random.randn(1)
b = paddle.to_tensor(b, dtype="float32", stop_gradient=False)
# 循环迭代
for t in range(10):
# 计算平方差损失
y_ = a * x_train + b
loss = paddle.sum((y_ - y_train) ** 2)
# 自动计算梯度
loss.backward()
# 更新参数(梯度下降),学习率默认使用1e-3
a = a.detach() - 1e-3 * float(a.grad)
b = b.detach() - 1e-3 * float(b.grad)
a.stop_gradient = False
b.stop_gradient = False
# 输出当前轮的目标函数值L
print("epoch: {}, loss: {}".format(t, (float(loss))))
# 训练结束,终止a和b的梯度计算
a.stop_gradient = True
b.stop_gradient = True
# 可视化输出
x_pred = paddle.arange(0, 15)
y_pred = a * x_pred + b
plt.plot(x_train.numpy(), y_train.numpy(), "go", label="Original Data")
plt.plot(x_pred.numpy(), y_pred.numpy(), "r-", label="Fitted Line")plt.xlabel("investment")
plt.ylabel("income")plt.legend()plt.savefig("result.png")
# 预测第16年的收益值
x = 12.5
y = a * x + b
print(y.numpy()) 上述代码对每轮迭代的目标函数进行了输出,同时预测了第16年的收益值,结果如下:
epoch: 0, loss: 9141.90625
epoch: 1, loss: 1103.665283203125
epoch: 2, loss: 397.5347900390625
epoch: 3, loss: 335.0281982421875
epoch: 4, loss: 329.02337646484375
epoch: 5, loss: 327.982421875
epoch: 6, loss: 327.381103515625
epoch: 7, loss: 326.8223571777344
epoch: 8, loss: 326.2711486816406
epoch: 9, loss: 325.72442626953125
[44.96492]可以看到,随着迭代的不断进行,目标函数逐渐减少,说明模型的预测输出越来越接近真值。最终训练好的模型所预测的第16年的收益值与上一节使用导数法求解的标准解非常接近,验证了梯度下降算法的有效性。
梯度下降法拟合结果如图2.29所示。
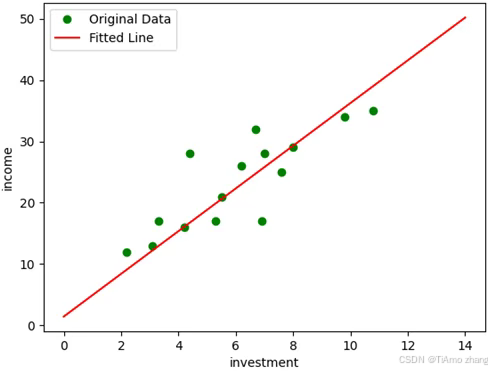
从拟合结果看到,利用PaddlePaddle自动帮助求导,通过梯度下降迭代更新模型参数,最后得到了令人满意的结果,拟合出来的直线基本吻合数据的分布。整个过程不需要手工计算梯度,实现非常简单。
注意,上述代码使用了随机值来初始化模型参数,因此每次运算的结果可能略有不同。另外,使用了固定的学习率1e-3,并得到了一个比较好的训练结果。如果训练过程中目标函数没有逐步下降,那么就需要适当调整学习率重新训练。
本节案例是一个非常简单的使用PaddlePaddle进行机器学习的示例,旨在帮助读者熟悉和巩固PaddlePaddle的基本使用方法。虽然任务简单,但是该示例“五脏俱全”,整个建模学习过程分为4个部分,如图2.30所示。
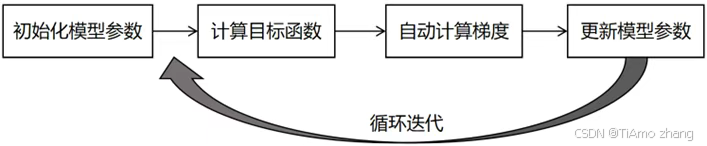
对于后面的深度学习任务,也会按照上述方式进行模型训练。下面正式开始介绍如何基于PaddlePaddle实现更复杂的深度学习图像应用。