在机器学习中,分类任务是最常见的应用场景之一。而逻辑回归(Logistic Regression),尽管名字中有“回归”,实际上是一种非常强大且广泛应用的二分类模型。它简单、高效、可解释性强,是数据科学初学者入门分类问题的首选算法。
本文将带你从数学原理、模型构建、代码实现到模型评估,全面掌握逻辑回归的核心知识,并通过两个真实案例(癌症分类与用户流失预测)进行实战演练。
一、什么是逻辑回归?
1.1 应用场景
逻辑回归是解决二分类问题的利器。常见应用场景包括:
- 医疗诊断:判断肿瘤是良性还是恶性
- 金融风控:预测用户是否会违约
- 用户行为:预测用户是否会流失、是否会点击广告
- 营销转化:预测客户是否会购买某产品
它输出的是一个介于0和1之间的概率值,表示样本属于正类的可能性。
二、核心数学基础
在深入逻辑回归原理之前,我们需要理解几个关键的数学概念。
2.1 Sigmoid 函数
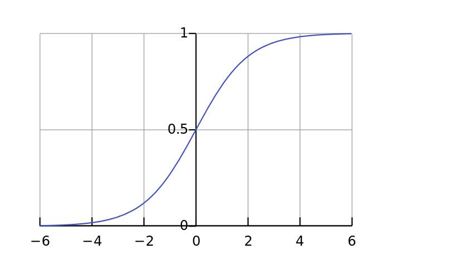
逻辑回归的核心是 Sigmoid 函数,它将任意实数映射到 (0, 1) 区间,非常适合表示概率。
公式如下:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
其中 z = w x + b z = wx + b z=wx+b 是线性回归的输出。
- 当 z → + ∞ z \to +\infty z→+∞, σ ( z ) → 1 \sigma(z) \to 1 σ(z)→1
- 当 z → − ∞ z \to -\infty z→−∞, σ ( z ) → 0 \sigma(z) \to 0 σ(z)→0
- 当 z = 0 z = 0 z=0, σ ( z ) = 0.5 \sigma(z) = 0.5 σ(z)=0.5
我们通常以 0.5 为阈值:若输出 > 0.5,预测为正类(1);否则为负类(0)。
2.2 极大似然估计(Maximum Likelihood Estimation)
逻辑回归的参数学习依赖于极大似然估计。
核心思想:在所有可能的参数中,选择一个能让已观测到的数据出现概率最大的参数作为估计值。
举个例子:
假设有一枚不均匀硬币,正面朝上的概率为 θ \theta θ。抛6次,结果为:{正, 反, 反, 正, 正, 正}。
出现该结果的概率为:
P ( D ∣ θ ) = θ ⋅ ( 1 − θ ) ⋅ ( 1 − θ ) ⋅ θ ⋅ θ ⋅ θ = θ 4 ( 1 − θ ) 2 P(D|\theta) = \theta \cdot (1-\theta) \cdot (1-\theta) \cdot \theta \cdot \theta \cdot \theta = \theta^4 (1-\theta)^2 P(D∣θ)=θ⋅(1−θ)⋅(1−θ)⋅θ⋅θ⋅θ=θ4(1−θ)2
我们的目标是找到使 P ( D ∣ θ ) P(D|\theta) P(D∣θ) 最大的 θ \theta θ 值。通过求导或数值方法,可得 θ = 0.67 \theta = 0.67 θ=0.67。
这就是极大似然估计的思想——“看上去最可能发生”的那个参数值。
三、逻辑回归原理详解
3.1 模型结构
逻辑回归可以看作是在线性回归的基础上,通过 Sigmoid 函数将输出转换为概率。
步骤如下:
- 计算线性组合: z = w 1 x 1 + w 2 x 2 + . . . + w n x n + b z = w_1x_1 + w_2x_2 + ... + w_nx_n + b z=w1x1+w2x2+...+wnxn+b
- 将 z z z 输入 Sigmoid 函数: h w ( x ) = σ ( z ) = 1 1 + e − z h_w(x) = \sigma(z) = \frac{1}{1 + e^{-z}} hw(x)=σ(z)=1+e−z1
- 设置阈值(如 0.5)进行分类:
- 若 h w ( x ) > 0.5 h_w(x) > 0.5 hw(x)>0.5,预测为正类(1)
- 否则预测为负类(0)
3.2 模型目标:输出概率
逻辑回归用于解决二分类问题,其核心是输出样本属于正类(类别1)的概率。
我们使用 Sigmoid 函数将线性组合 z = w T x + b z = w^T x + b z=wTx+b 映射为概率:
P ( y = 1 ∣ x ) = σ ( z ) = 1 1 + e − z , 其中 z = w T x + b P(y=1|x) = \sigma(z) = \frac{1}{1 + e^{-z}}, \quad \text{其中 } z = w^T x + b P(y=1∣x)=σ(z)=1+e−z1,其中 z=wTx+b
相应地,属于负类的概率为:
P ( y = 0 ∣ x ) = 1 − σ ( z ) P(y=0|x) = 1 - \sigma(z) P(y=0∣x)=1−σ(z)
为了统一表达,我们可以将两个情况合并为一个公式:
P ( y ∣ x ) = [ σ ( z ) ] y ⋅ [ 1 − σ ( z ) ] 1 − y P(y|x) = [\sigma(z)]^y \cdot [1 - \sigma(z)]^{1-y} P(y∣x)=[σ(z)]y⋅[1−σ(z)]1−y
说明:这个表达式非常巧妙:
- 当 y = 1 y = 1 y=1 时,第二项 [ 1 − σ ] 0 = 1 [1-\sigma]^{0} = 1 [1−σ]0=1,只剩下 σ ( z ) \sigma(z) σ(z)
- 当 y = 0 y = 0 y=0 时,第一项 σ 0 = 1 \sigma^0 = 1 σ0=1,只剩下 1 − σ ( z ) 1 - \sigma(z) 1−σ(z)
3.3 构造似然函数(Likelihood)
我们希望找到一组参数 w , b w, b w,b,使得模型在训练数据上的预测概率最大,即让模型对真实标签的预测尽可能“可信”。
对于 N N N 个独立同分布的样本,总的似然函数为:
L ( w , b ) = ∏ i = 1 N P ( y ( i ) ∣ x ( i ) ; w , b ) = ∏ i = 1 N [ σ ( z ( i ) ) ] y ( i ) [ 1 − σ ( z ( i ) ) ] 1 − y ( i ) L(w, b) = \prod_{i=1}^N P(y^{(i)}|x^{(i)}; w, b) = \prod_{i=1}^N \left[\sigma(z^{(i)})\right]^{y^{(i)}} \left[1 - \sigma(z^{(i)})\right]^{1 - y^{(i)}} L(w,b)=i=1∏NP(y(i)∣x(i);w,b)=i=1∏N[σ(z(i))]y(i)[1−σ(z(i))]1−y(i)
这个函数表示:在参数 w , b w,b w,b 下,观测到当前所有样本标签的联合概率。
我们的目标是最大化这个似然函数。
3.4 取对数似然(Log-Likelihood)
由于乘积形式难以优化(尤其是数值不稳定),我们对似然函数取对数,将其转化为求和形式:
ℓ ( w , b ) = log L ( w , b ) = ∑ i = 1 N [ y ( i ) log σ ( z ( i ) ) + ( 1 − y ( i ) ) log ( 1 − σ ( z ( i ) ) ) ] \ell(w, b) = \log L(w, b) = \sum_{i=1}^N \left[ y^{(i)} \log \sigma(z^{(i)}) + (1 - y^{(i)}) \log (1 - \sigma(z^{(i)})) \right] ℓ(w,b)=logL(w,b)=i=1∑N[y(i)logσ(z(i))+(1−y(i))log(1−σ(z(i)))]
最大化对数似然 ℓ ( w , b ) \ell(w, b) ℓ(w,b) 等价于最大化原始似然 L ( w , b ) L(w, b) L(w,b)。
3.5 转化为损失函数(Loss Function)
在机器学习中,我们通常使用梯度下降法来最小化一个损失函数。因此,我们将“最大化对数似然”转化为“最小化其负值”。
定义损失函数为负对数似然(Negative Log-Likelihood):
J ( w , b ) = − ℓ ( w , b ) = − ∑ i = 1 N [ y ( i ) log σ ( z ( i ) ) + ( 1 − y ( i ) ) log ( 1 − σ ( z ( i ) ) ) ] J(w, b) = -\ell(w, b) = -\sum_{i=1}^N \left[ y^{(i)} \log \sigma(z^{(i)}) + (1 - y^{(i)}) \log (1 - \sigma(z^{(i)})) \right] J(w,b)=−ℓ(w,b)=−i=1∑N[y(i)logσ(z(i))+(1−y(i))log(1−σ(z(i)))]
为了得到平均损失,我们通常除以样本数 N N N:
J ( w , b ) = − 1 N ∑ i = 1 N [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] J(w, b) = -\frac{1}{N} \sum_{i=1}^N \left[ y^{(i)} \log \hat{y}^{(i)} + (1 - y^{(i)}) \log (1 - \hat{y}^{(i)}) \right] J(w,b)=−N1i=1∑N[y(i)logy^(i)+(1−y(i))log(1−y^(i))]
其中 y ^ ( i ) = σ ( w T x ( i ) + b ) \hat{y}^{(i)} = \sigma(w^T x^{(i)} + b) y^(i)=σ(wTx(i)+b)。
这就是逻辑回归的标准损失函数,也被称为二元交叉熵损失(Binary Cross-Entropy Loss)。
3.6 为什么这个损失函数合理?
我们来分析损失函数的行为:
- 当真实标签 y = 1 y = 1 y=1 时,损失为 − log ( y ^ ) -\log(\hat{y}) −log(y^):
- 若预测概率 y ^ → 1 \hat{y} \to 1 y^→1,损失 → 0 \to 0 →0
- 若预测概率 y ^ → 0 \hat{y} \to 0 y^→0,损失 → + ∞ \to +\infty →+∞
- 当真实标签 y = 0 y = 0 y=0 时,损失为 − log ( 1 − y ^ ) -\log(1 - \hat{y}) −log(1−y^):
- 若预测概率 y ^ → 0 \hat{y} \to 0 y^→0,损失 → 0 \to 0 →0
- 若预测概率 y ^ → 1 \hat{y} \to 1 y^→1,损失 → + ∞ \to +\infty →+∞
这说明:
- 模型对正确预测给予低惩罚(损失小)
- 对错误预测(尤其是高置信度的错误)给予严厉惩罚(损失趋向无穷)
此外,该损失函数是关于参数 w w w 的凸函数,保证了梯度下降等优化方法能找到全局最优解。
四、Scikit-learn 中的逻辑回归 API
Python 的 scikit-learn 库提供了简洁的逻辑回归实现:
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(
solver='liblinear', # 优化算法
penalty='l2', # 正则化类型:'l1' 或 'l2'
C=1.0, # 正则化强度,C越小正则化越强
random_state=42
)
参数说明:
| 参数 | 说明 |
|---|---|
solver |
优化算法,小数据集用 'liblinear',大数据用 'sag' 或 'saga' |
penalty |
正则化类型,'l1'(Lasso)、'l2'(Ridge) |
C |
正则化强度,值越小,正则化越强 |
五、实战案例一:乳腺癌分类
5.1 数据集介绍
- 数据来源:威斯康星乳腺癌数据集
- 样本数:699 条
- 特征:9 个医学特征(如细胞核大小、形状等)
- 标签:2(良性),4(恶性)
- 缺失值:16 个,用
?表示
5.2 处理流程
- 数据加载与清洗:替换
?为 NaN,删除缺失值 - 特征与标签分离:前9列为特征,最后一列为标签
- 数据集划分:训练集 80%,测试集 20%
- 特征标准化:使用
StandardScaler - 模型训练与预测
- 模型评估
5.3 代码实现
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 1. 加载数据
data = pd.read_csv('data/breast-cancer-wisconsin.csv')
data = data.replace('?', np.nan).dropna()
# 2. 特征与标签
X = data.iloc[:, 1:-1] # 第2列到倒数第2列
y = data['Class']
# 3. 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=21)
# 4. 特征标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 5. 训练模型
model = LogisticRegression()
model.fit(X_train, y_train)
# 6. 预测与评估
y_pred = model.predict(X_test)
print(f"准确率: {accuracy_score(y_test, y_pred):.4f}")
准确率这一指标不够严谨,因为在实际诊疗中,我们无法直接告知患者患病概率的具体数值。因此我们需要增加一些新的指标。
六、分类模型评估方法
准确率(Accuracy)并不能全面反映模型性能,尤其在类别不平衡时。我们需要更精细的评估指标。
6.1 混淆矩阵(Confusion Matrix)
| 预测为正 | 预测为负 | |
|---|---|---|
| 实际为正 | TP(真正例) | FN(伪反例) |
| 实际为负 | FP(伪正例) | TN(真反例) |
- 真实值是 正例 的样本中,被分类为 正例 的样本数量有多少,叫做真正例(TP,True Positive)
- 真实值是 正例 的样本中,被分类为 假例 的样本数量有多少,叫做伪反例(FN,False Negative)
- 真实值是 假例 的样本中,被分类为 正例 的样本数量有多少,叫做伪正例(FP,False Positive)
- 真实值是 假例 的样本中,被分类为 假例 的样本数量有多少,叫做真反例(TN,True Negative)
6.2 精确率(Precision)——查准率
预测为正的样本中,有多少是真正的正例。
Precision = T P T P + F P \text{Precision} = \frac{TP}{TP + FP} Precision=TP+FPTP
6.3 召回率(Recall)——查全率
所有真正的正例中,有多少被成功预测出来。
Recall = T P T P + F N \text{Recall} = \frac{TP}{TP + FN} Recall=TP+FNTP
6.4 F1-Score —— 精确率与召回率的调和平均
F 1 = 2 ⋅ Precision ⋅ Recall Precision + Recall F1 = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} F1=2⋅Precision+RecallPrecision⋅Recall
import pandas as pd
from sklearn.metrics import confusion_matrix,precision_score,recall_score,f1_score
# todo 1、定义数据集(真实数据)
y_train = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性', '良性', '良性', '良性']
# todo 2、定义标签名
label = ['恶性','良性']
df_label = ['恶性(正例)','良性(假例)']
# todo 3、定义预测结果A、B(预测数据)
y_pre_A = ['恶性', '恶性', '恶性', '良性', '良性', '良性', '良性', '良性', '良性', '良性']
y_pre_B = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性']
# todo 4、计算混淆矩阵
cm_A = confusion_matrix(y_train, y_pre_A, labels=label)
cm_B = confusion_matrix(y_train, y_pre_B, labels=label)
# todo 5、将混淆矩阵转为DataFrame
df_A = pd.DataFrame(cm_A, index=df_label, columns=df_label)
df_B = pd.DataFrame(cm_B, index=df_label, columns=df_label)
print(f"混淆矩阵A:{df_A}")
print(f"混淆矩阵B:{df_B}")
# todo 6、计算精确率
precision_A = precision_score(y_train, y_pre_A, pos_label='恶性')
precision_B = precision_score(y_train, y_pre_B, pos_label='恶性')
print(f"精确率A:{precision_A}")
print(f"精确率B:{precision_B}")
# todo 7、计算召回率
recall_A = recall_score(y_train, y_pre_A, pos_label='恶性')
recall_B = recall_score(y_train, y_pre_B, pos_label='恶性')
print(f"召回率A:{recall_A}")
print(f"召回率B:{recall_B}")
# todo 8、计算F1-score
f1_A = f1_score(y_train, y_pre_A, pos_label='恶性')
f1_B = f1_score(y_train, y_pre_B, pos_label='恶性')
print(f"F1-scoreA:{f1_A}")
print(f"F1-scoreB:{f1_B}")
6.5 ROC 曲线与 AUC 指标
- ROC曲线(Receiver Operating Characteristic curve):横轴为 FPR(假正率),纵轴为 TPR(真正率)。是一种常用于评估分类模型性能的可视化工具,它将模型在不同阈值下的表现以曲线的形式展现出来。
- FPR = F P F P + T N \text{FPR} = \frac{FP}{FP + TN} FPR=FP+TNFP
- TPR = T P T P + F N \text{TPR} = \frac{TP}{TP + FN} TPR=TP+FNTP
真正率TPR与假正率FPR
- 正样本中被预测为正样本的概率TPR (True Positive Rate)
- 负样本中被预测为正样本的概率FPR (False Positive Rate)
通过这两个指标可以描述模型对正/负样本的分辨能力
- AUC(Area Under the ROC Curve):ROC曲线下的面积,值越接近1,模型性能越好。
- 当AUC=0.5时,表示分类器的性能等同于随机猜测
- 当AUC=1时,表示分类器的性能完美,能够完全正确地将正负例分类。
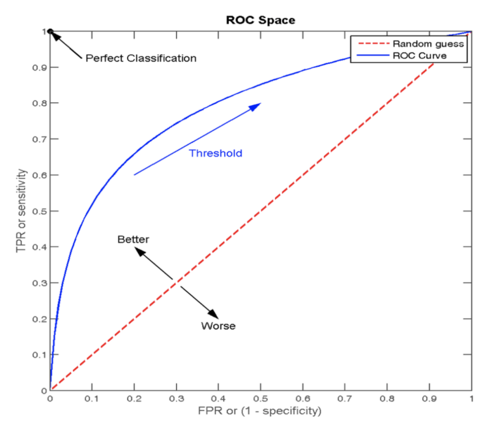
ROC 曲线图像中,4 个特殊点的含义:点坐标说明:图像x轴FPR/y轴TPR, 任意一点坐标A(FPR值, TPR值)
- 点(0, 0) :所有的负样本都预测正确,所有的正样本都预测为错误 。相当于点的(FPR值0, TPR值0)
- 点(1, 0) :所有的负样本都预测错误,所有的正样本都预测错误。相当于点的(FPR值1, TPR值0) —— ( 最不好的效果)
- 点(1, 1):所有的负样本都预测错误,表示所有的正样本都预测正确。相当于点的(FPR值1,TPR值1)
- 点(0, 1):所有的负样本都预测正确,表示所有的正样本都预测正确 。相当于点的(FPR值0,TPR值)—— ( 最好的效果)
ROC曲线上的每个点代表模型在不同阈值下的性能表现
从图像上来看:曲线越靠近 (0,1) 点则模型对正负样本的辨别能力就越强
# AUC的计算api
from sklearn.metrics import roc_auc_score
auc = roc_auc_score(y_test, y_pred)
'''
计算ROC曲线面积,即AUC值
y_true:每个样本的真实类别,必须为0(反例),1(正例)标记
y_score:预测得分,可以是正例的估计概率、置信值或者分类器方法的返回值
'''
# 分类评估报告api
from sklearn.metrics import classification_report
report=classification_report(y_true, y_pred, labels=[], target_names=None )
'''
y_true:真实目标值
y_pred:估计器预测目标值
labels:指定类别对应的数字
target_names:目标类别名称
return:每个类别精确率与召回率
'''
七、实战案例二:电信客户流失预测
7.1 数据集介绍
- 样本数:7043 条
- 特征:21 个,包括性别、合约类型、月消费、是否开通网络服务等
- 标签:
Churn(是否流失)
7.2 处理流程
- 类别特征编码:使用
pd.get_dummies()进行 One-Hot 编码 - 特征筛选:分析哪些特征对流失影响大(如按月签约、电子支付等)
- 模型训练
- 评估指标:准确率 + AUC
7.3 代码
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import precision_score, roc_auc_score,recall_score,f1_score,roc_curve
import matplotlib.pyplot as plt
# todo 1、 定义函数 ,实现数据预处理
def dm01_data_preprocessing():
# 1、读取数据
data = pd.read_csv(r'../../data/churn.csv')
# data.info()
# 、2、因为上述的字段Churn、gender 是字符串类型,所以我们需要对其进行转换,对齐做one-hot编码处理
# 底层数据是boolean值 ,布尔值和int类型直接可以转换
data = pd.get_dummies(data)
# print(data.head())
# 3、删除列 ,因为热编码之后,被热编码列 多出一个列 ,我们要删除掉
data.drop(['gender_Female','Churn_No'], axis=1,inplace=True)
# print(data.head())
# 修改一下标签名 Churn_Yes flag
data.rename(columns={'Churn_Yes': 'flag', 'gender_Male': 'gender'}, inplace=True)
# print(data.head())
# 5、因为这里是流失数据 查看标签是否均衡
print(data['flag'].value_counts())
return data
# todo 2、定义函数,实现逻辑回归模型训练与评估
def dm02_logistic_regression():
data = dm01_data_preprocessing()
# print(data.head())
# 6、定义数据集
x = data[['Contract_Month', 'internet_other', 'PaymentElectronic']]
y = data['flag']
# 7、划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=22)
# 8、特征工程_标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 9、模型训练
es = LogisticRegression()
es.fit(x_train, y_train)
# 10、模型预测
y_pred = es.predict(x_test)
y_pred_proba = es.predict_proba(x_test)[:, 1] # 获取正类的概率
# 11、模型评估
accuracy = es.score(x_test, y_test)
recall = recall_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_pred_proba)
print(f"准确率:{accuracy}")
print(f"精确率:{precision}")
print(f"召回率:{recall}")
print(f"F1-score:{f1}")
print(f"ROC AUC指数:{roc_auc}")
return y_test,y_pred_proba,roc_auc
# todo 3、定义函数,实现ROC曲线可视化
def dm03_plot_roc_curve():
y_test, y_pred_proba, roc_auc = dm02_logistic_regression()
# 计算ROC曲线的坐标点
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba)
# 绘制ROC曲线
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
if __name__ == '__main__':
# dm01_data_preprocessing()
# dm02_logistic_regression()
dm03_plot_roc_curve()
结果截图:
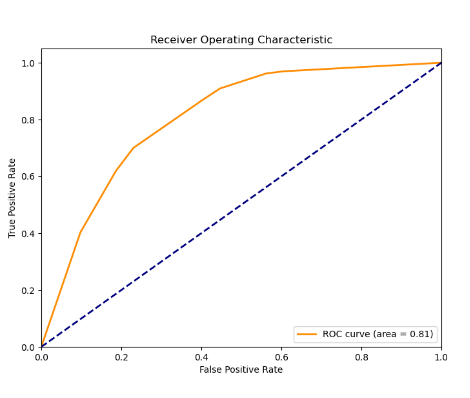
数据获取:跳转gitee获取数据集
八、总结
逻辑回归虽然简单,但其背后的数学思想(Sigmoid、极大似然、对数损失)非常深刻。它不仅是分类任务的基石,也为理解更复杂的模型(如神经网络)打下基础。