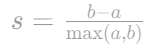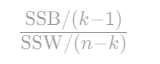机器学习-聚类

​​一、聚类算法基础概念​​

1. ​​定义​​

   • 聚类是一种​​无监督学习​​方法，根据样本间的相似性自动划分到不同类别，无需预先标注数据。
   • ​​核心目标​​：发现数据内在结构和模式（如客户分群、图像分割）。

2. ​​相似度衡量​​

   • ​​常用方法​​：欧式距离（默认），其他可选曼哈顿距离、余弦相似度等。
   • ​​关键点​​：相似度计算方式直接影响聚类结果（如按生物特征或地理信息聚类结果不同）。

3. ​​应用场景​​

   • 商业分析：用户画像、广告推荐、客户分群。
   • 数据挖掘：新闻聚类、异常检测（信用卡欺诈）。
   • 技术领域：图像分割、基因功能分析、搜索引擎优化。

4. ​​算法分类​​

   ​​分类方式​​	​​类型​​	​​代表算法​​
   ​​聚类颗粒度​​	粗聚类、细聚类	-
   ​​实现方法​​	基于质心	K-means

​​二、K-means算法详解​​

1. ​​API使用（sklearn）​​

   from sklearn.cluster import KMeans  
   # 初始化模型  
   model = KMeans(n_clusters=4, random_state=22)  
   # 训练并预测类别  
   y_pred = model.fit_predict(X)  

   • ​​参数​​：n_clusters（聚类中心数量）。
   • ​​方法​​：
     • fit_predict()：训练模型并返回样本类别标签。
     • cluster_centers_：获取聚类中心坐标。

2. ​​实现流程（迭代优化）​​

   1. ​​随机初始化​​：选择K个样本作为初始质心。
   2. ​​距离计算​​：计算所有样本到K个质心的距离（欧式距离）。
   3. ​​样本分配​​：将样本分配到距离最近的质心类别。
   4. ​​更新质心​​：重新计算每个类别的均值作为新质心。
   5. ​​收敛判断​​：重复步骤2-4直至质心不再变化。

   ​​示例​​：

   • 数据点：[(1,2), (1,4), (3,1), (3,5)]，初始质心(1,2), (3,1)
   • 第一轮：类别1: [(1,2), (1,4)] → 新质心(1,3)；类别2: [(3,1), (3,5)] → 新质心(3,3)
   • 第二轮：质心更新后重新分配样本，直至稳定。

​​三、聚类效果评估方法​​

1. ​​SSE（误差平方和）​​

   • ​​公式​​：
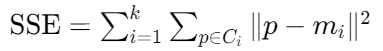
   • ​​意义​​：值越小表示簇内样本越紧密，聚类效果越好。

2. ​​肘部法（Elbow Method）​​

   • ​​步骤​​：
     1. 遍历K值（如K=1到10），计算各K值对应的SSE。
     2. 绘制SSE随K值变化的曲线。
     3. ​​最佳K值​​：SSE下降速率骤减的拐点（如右图K=4）。
   • ​​代码​​：

     sse = []  
     for k in range(1, 11):  
         model = KMeans(n_clusters=k).fit(X)  
         sse.append(model.inertia_)  # inertia_即SSE  
     plt.plot(range(1,11), sse, 'o-')  

3. ​​轮廓系数（Silhouette Coefficient）​​

   • ​​范围​​：[-1, 1]，值越大表示簇内紧致、簇间分离度高。
   • ​​计算​​：
     • a：样本到同簇其他点的平均距离（内聚度）。
     • b：样本到最近其他簇的平均距离（分离度）。
     • 
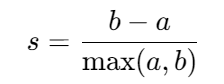
   • ​​API​​：sklearn.metrics.silhouette_score(X, y_pred)

4. ​​CH指数（Calinski-Harabasz）​​

   • ​​公式​​：​
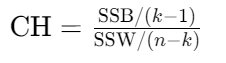
     • SSB：簇间距离平方和（越大越好）。
     • SSW：簇内距离平方和（越小越好）。
   • ​​特点​​：同时考虑聚类紧密度、分离度和质心数量。

​​四、实战案例：客户价值分析​​

1. ​​数据集​​

   • 字段：客户性别、年龄、年收入、消费指数。
   • ​​目标​​：划分客户群，识别高价值群体（如高收入高消费人群）。

2. ​​步骤​​

   import pandas as pd  
   from sklearn.cluster import KMeans  
   
   # 加载数据  
   data = pd.read_csv('customers.csv')  
   X = data[['AnnualIncome', 'SpendingScore']]  
   
   # 寻找最佳K值（肘部法+轮廓系数）  
   sse, sc = [], []  
   for k in range(2, 11):  
       model = KMeans(n_clusters=k).fit(X)  
       sse.append(model.inertia_)  
       sc.append(silhouette_score(X, model.predict(X)))  
   
   # 确定K=5（拐点+轮廓系数峰值）  
   model = KMeans(n_clusters=5).fit(X)  
   data['Cluster'] = model.predict(X)  
   
   # 可视化  
   plt.scatter(data['AnnualIncome'], data['SpendingScore'], c=data['Cluster'])  
   plt.scatter(model.cluster_centers_[:,0], model.cluster_centers_[:,1], s=300, c='black')  

3. ​​结论​​

   • ​​黄金客户群​​：右上角簇（高收入、高消费）→ 重点维护对象。
   • ​​潜在客户​​：高收入低消费簇 → 针对性促销提升消费意愿。

​​五、易错点总结​​

1. ​​相似度衡量误区​​

   • 错误说法：聚类只能使用欧式距离（×）
   • 正确：可灵活选用距离/相似度计算方法（如文本聚类常用余弦相似度）。

2. ​​K-means局限​​

   • 对初始质心敏感 → 多次运行取最优解。
   • 仅适用于凸数据集 → 非凸数据需用DBSCAN等算法。

3. ​​评估指标选择​​

   • ​​SSE​​：侧重簇内紧密性，需配合肘部法使用。
   • ​​SC系数​​：综合内聚度和分离度，适用于多类别比较。
   • ​​CH指数​​：适合需平衡簇数量与效果的场景。

​​附：核心公式速查表​​

• ​​SSE​​：簇内样本到质心距离平方和
• ​​SC系数​​：
• ​​CH指数​​：