计算机系统硬件基本组成
- 计算机系统 = 硬件 + 软件 (协同工作运行)
- 计算机基本硬件 = (运算器 + 控制器) + 存储器 + (输入设备 + 输出设备) PS. 还得是冯诺依曼
- 硬件核心 ⇒ 中央处理单元(Central Processing Unit,CPU)= 运算器 + 控制器 + 等部件⇒ 数据加工
- 记忆设备 ⇒ 存储器 = 内部存储器 + 外部存储器
内部存储器 ⇒ 临时数据,速度快,容量小 ⇒ 内存
外部存储器 ⇒ 长期数据,速度慢,容量大 ⇒ 硬盘 - 外设 ⇒ 输入设备 + 输出设备 ⇒ 输入数据和指令,输出运行结果
中央处理单元
CPU的功能
CPU ⇒ 负责获取程序指令、对指令进行译码并加以执行。
- 程序控制,程序的执行顺序(重要功能)
- 操作控制,指令的操作信号送到对应的部件,控制部件按照指令的功能进行相应操作(让谁做,做什么操作)
- 时间控制,指令执行的时间、持续时间等(何时做,做多久,做的顺序)
- 数据处理,对数据进行算术、逻辑计算等等,处理的结果被人们所有(对数据进行加工处理是最根本的任务)
- 异常处理,系统内外部的中断做出响应
CPU的组成
CPU === 运算器 + 控制器 + 寄存器组 + 内部总线等部件
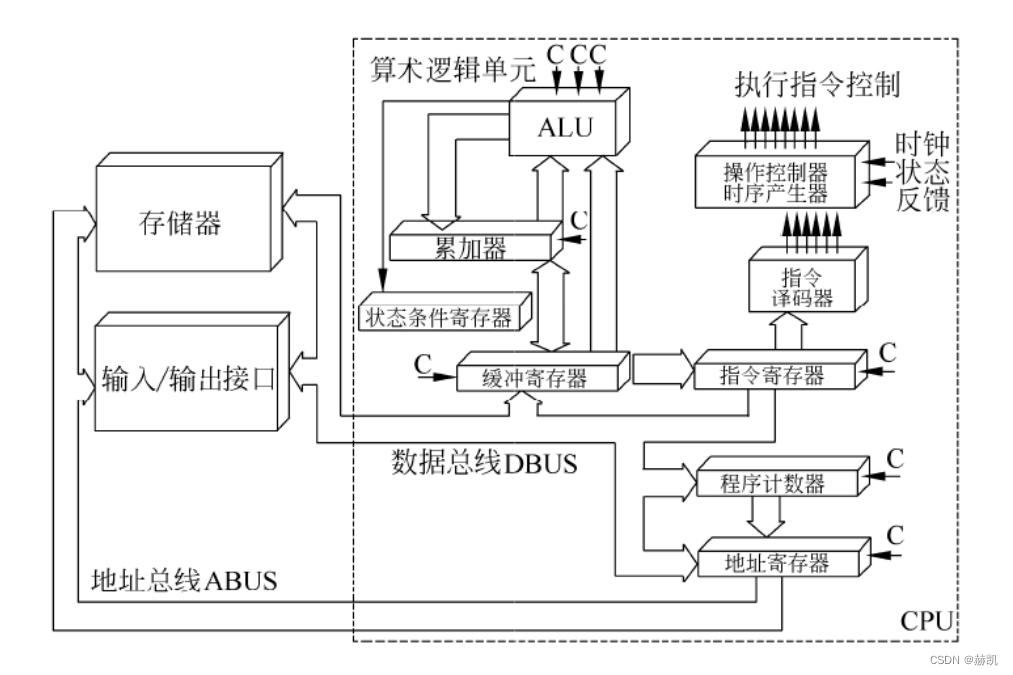
- 运算器
运算器 = 算术逻辑单元(Arithmetic and Logic Unit, ALU)+ 累加寄存器 + 数据缓冲寄存器 + 状态条件寄存器等 ⇒ 数据加工部件,用于完成计算机的各种运算。
->>>>> 控制器 控制 运算器<<<<<-
1 运算器 ⇒ 执行所有的算术运算和所有的逻辑运算并进行逻辑测试
2 算术逻辑单元(ALU)⇒ 处理数据,实现数据的算术运算和逻辑运算
3 累加寄存器(AC)⇒ 简称累加器,通用寄存器,为运算器的ALU执行运算时提供工作区。也就是临时存放运算的数据。(一般运算都是两个数字奥)
4 数据缓存寄存器(DR)⇒ 作为CPU和内存、外部设备之间数据传送的中转站,也是操作速度上的缓冲
5 状态条件寄存器(PSW)⇒ 保存当前指令执行完成过后的状态。(让大家知道我做了什么操作) - 控制器
运算器只是一个没得感情的工具人,只会运算,而控制器用于控制整个CPU的工作,决定了计算机运行过程的自动化。不仅要保证程序正确执行,而且还要能够处理异常事件。
– 控制器 包含 指令控制逻辑、时许控制逻辑、总线控制逻辑和中断控制逻辑等 –
1 逻辑控制逻辑 完成 取指令、分析指令和执行指令的操作,过程分为取指令、指令译码、按指令操作码执行、形成下一条指令地址等步骤。
<1> 指令寄存器(IR)。CPU先从内存取出指令,放在缓冲寄存器中,再送到 IR 暂存,指令译码器根据 IR 的内容产生各种微操作指令,控制其他的组成部件工作,完成所需的功能。(操作层面)
<2> 程序计数器(PC)。PC可以寄存信息,也可以计数,又称为指令计数器。程序执行 ⇒ 顺序执行、转移执行。程序执行前,将程序的起始地址放进 PC 中,PC 的内容就是程序第一条指令的地址。在程序执行过程中,CPU会自动修改 PC 的内容,让其保持的总是要执行的系一条指令地址。顺序执行就是对 PC 加1,转移的时候,就是在当前的指令地址加一个向前或向后的位移量得到。(那我理解就是,PC 有一长串指令地址,只要顺着往下走就可以了)
<3> 地址寄存器(AR)。AR 保存当前 CPU 所访问的内存单元地址。因为CPU和内存操作速度有差异,需要AR保持地址信息,直到内存的读/写操作完成为止。(类似数据层面)
<4> 指令译码器(ID)。指令 = 操作码 + 地址码,对指令的操作码字段进行分析解释,要知道进行什么操作,向操作控制器发出具体的控制信号,控制各部件工作,完成所需的功能。
2 时序控制逻辑 为每条指令按时间顺序提供应有的控制信号
3 总线逻辑 为多个功能部件服务的信息通路的控制电路,也就是将各种部件连在一起的的线
4 中断控制逻辑 用于控制各种中断请求,根据优先级对中断请求进行排队,逐个交给 CPU 处理 - 寄存器组
寄存器组 = 专用寄存器 + 通用寄存器,运算器和控制器的寄存器是专用寄存器,作用是固定的。通用寄存器用途广泛并可以自定义其用途,其数目因处理器不同有所差异。
多核 CPU
核心就是内核,是CPU最重要的组成部分,具有固定的逻辑结构,一级缓存、二级缓存、执行单元、指令级单元和总线接口等逻辑单元都会有的合理布局。
多核最大的有点是,可以满足用户同时进行多任务处理的要求。单核多线程 CPU 是交替地转换执行多个任务,只不过交替转换时间短,用户感觉不出来,但是多核理论上,各自核心负责各自的任务,速度就更快。
想要发挥多核CPU的全部威力,需要操作系统能够及时、合理地个各个核分配任务和资源,也需要应用软件在运行时可以把并行的线程同时交付给多个核心分别处理。
数据表示
在计算机中,数值的表示形式称为机器数,采用二进制,数的符号就是0和1,小数点则隐含,表示不占位置。机器数对应的实际数值称为数的真值。
机器数 = 无符号数 + 带符号数
无符号数 = 纯整数(小数点位置在机器数最低为之后) + 纯小数(小数点位置在机器数最高位之前)小数点位置是约定的,不会表示出来。
带符号数 机器数最高位表正负的符号位,其余位则表示数值
来看老生常谈的原码、反码和补码等,这些编码方法称为码制。
- 原码、反码、补码和移码,在机器运算的时候都是用补码进行运算的,可以用加法表示减法。
1 ------- 原码表示法 -------
数值 X X X的原码记为 [ X ] 原 [X]_原 [X]原,如果机器字长为 n n n,原码定义如下:
X X X纯整数
[ X ] 原 = { X 0 ⩽ X ⩽ 2 n − 1 − 1 2 n − 1 + ∣ X ∣ − ( 2 n − 1 − 1 ) ⩽ X ⩽ 0 [X]_原=\begin{cases} X & 0\leqslant X \leqslant 2^{n-1}-1 \\ 2^{n-1} + |X| & -(2^{n-1}-1) \leqslant X \leqslant 0 \end{cases} [X]原={X2n−1+∣X∣0⩽X⩽2n−1−1−(2n−1−1)⩽X⩽0
X X X纯小数
[ X ] 原 = { X 0 ⩽ X < 1 2 0 + ∣ X ∣ − 1 < X ⩽ 0 [X]_原=\begin{cases} X & 0\leqslant X <1 \\ 2^{0} + |X| & -1 < X \leqslant 0 \end{cases} [X]原={X20+∣X∣0⩽X<1−1<X⩽0
看个例子,如果字长为8,看下+1,-1,+127,-127,+45,-45,+0.5,-0.5的原码表示,首先明确,字长为8,除过最高位是表示正负,数值的话也就是7位, 2 7 2^7 27 = 128,128换算2进制,正好七位数进1,就是1000 0000。
[ + 1 ] 原 = 0 000 0001 [+1]_原=0\; 000\, 0001 [+1]原=00000001
[ − 1 ] 原 = 1 000 0001 [-1]_原=1\; 000\, 0001 [−1]原=10000001
[ + 127 ] 原 = 0 111 1111 [+127]_原=0\; 111\, 1111 [+127]原=01111111
[ − 127 ] 原 = 1 111 1111 [-127]_原=1\; 111\, 1111 [−127]原=11111111
[ + 45 ] 原 = 0 010 1101 [+45]_原=0\; 010\, 1101 [+45]原=00101101
[ − 45 ] 原 = 1 010 1101 [-45]_原=1\; 010\, 1101 [−45]原=10101101
[ + 0.5 ] 原 = 0 ⋄ 100 0000 [+0.5]_原=0\; \diamond100\, 0000 [+0.5]原=0⋄1000000
[ − 0.5 ] 原 = 1 ⋄ 100 0000 [-0.5]_原=1\; \diamond100\, 0000 [−0.5]原=1⋄1000000
⋄ \diamond ⋄是小数点位置
看出规律了,只要在范围内,就是把最高位的正负符号变一下。
[ + 0 ] 原 = 0 000 0000 [+0]_原=0\; 000\, 0000 [+0]原=00000000
[ − 0 ] 原 = 1 000 0000 [-0]_原=1\; 000\, 0000 [−0]原=10000000
2 ------- 反码表示法 -------
X X X纯整数
[ X ] 反 = { X 0 ⩽ X ⩽ 2 n − 1 − 1 2 n − 1 + X − ( 2 n − 1 − 1 ) ⩽ X ⩽ 0 [X]_反=\begin{cases} X & 0\leqslant X \leqslant 2^{n-1}-1 \\ 2^{n}-1 + X & -(2^{n-1}-1) \leqslant X \leqslant 0 \end{cases} [X]反={X2n−1+X0⩽X⩽2n−1−1−(2n−1−1)⩽X⩽0
X X X纯小数
[ X ] 反 = { X 0 ⩽ X < 1 2 − 2 − ( n − 1 ) + X − 1 < X ⩽ 0 [X]_反=\begin{cases} X & 0\leqslant X < 1 \\ 2-2^{-(n-1)} + X & -1 < X \leqslant 0 \end{cases} [X]反={X2−2−(n−1)+X0⩽X<1−1<X⩽0
把上面例子数的反码表示一下
[ + 1 ] 反 = 0 000 0001 [+1]_反=0\; 000\, 0001 [+1]反=00000001
[ − 1 ] 反 = 1 111 1110 [-1]_反=1\; 111\, 1110 [−1]反=11111110
[ + 127 ] 反 = 0 111 1111 [+127]_反=0\; 111\, 1111 [+127]反=01111111
[ − 127 ] 反 = 1 000 0000 [-127]_反=1\; 000\, 0000 [−127]反=10000000
[ + 45 ] 反 = 0 010 1101 [+45]_反=0\; 010\, 1101 [+45]反=00101101
[ − 45 ] 反 = 1 101 0010 [-45]_反=1\; 101\, 0010 [−45]反=11010010
[ + 0.5 ] 反 = 0 ⋄ 100 0000 [+0.5]_反=0\; \diamond100\, 0000 [+0.5]反=0⋄1000000
[ − 0.5 ] 反 = 1 ⋄ 011 1111 [-0.5]_反=1\; \diamond011\, 1111 [−0.5]反=1⋄0111111
看出规律了,只要在范围内,就是把1和0互换。
[ + 0 ] 反 = 0 000 0000 [+0]_反=0\; 000\, 0000 [+0]反=00000000
[ − 0 ] 反 = 1 111 1111 [-0]_反=1\; 111\, 1111 [−0]反=11111111
3 ------- 补码表示法 -------
[ X ] 补 = { X 0 ⩽ X ⩽ 2 n − 1 − 1 2 n + X − ( 2 n − 1 − 1 ) ⩽ X ⩽ 0 [X]_补=\begin{cases} X & 0\leqslant X \leqslant 2^{n-1}-1 \\ 2^{n} + X & -(2^{n-1}-1) \leqslant X \leqslant 0 \end{cases} [X]补={X2n+X0⩽X⩽2n−1−1−(2n−1−1)⩽X⩽0
X X X纯小数
[ X ] 补 = { X 0 ⩽ X < 1 2 + X − 1 ⩽ X < 0 [X]_补=\begin{cases} X & 0\leqslant X <1 \\ 2 + X & -1 \leqslant X < 0 \end{cases} [X]补={X2+X0⩽X<1−1⩽X<0
[ + 1 ] 补 = 0 000 0001 [+1]_补=0\; 000\, 0001 [+1]补=00000001
[ − 1 ] 补 = 1 111 1111 [-1]_补=1\; 111\, 1111 [−1]补=11111111
[ + 127 ] 补 = 0 111 1111 [+127]_补=0\; 111\, 1111 [+127]补=01111111
[ − 127 ] 补 = 1 000 0001 [-127]_补=1\; 000\, 0001 [−127]补=10000001
[ + 45 ] 补 = 0 010 1101 [+45]_补=0\; 010\, 1101 [+45]补=00101101
[ − 45 ] 补 = 1 101 0011 [-45]_补=1\; 101\, 0011 [−45]补=11010011
[ + 0.5 ] 补 = 0 ⋄ 100 0000 [+0.5]_补=0\; \diamond100\, 0000 [+0.5]补=0⋄1000000
[ − 0.5 ] 补 = 1 ⋄ 100 0000 [-0.5]_补=1\; \diamond100\, 0000 [−0.5]补=1⋄1000000
看出规律了,只要在范围内,就是把这个数的反码+1。
[ + 0 ] 补 = 0 000 0000 [+0]_补=0\; 000\, 0000 [+0]补=00000000
[ − 0 ] 补 = 0 000 0000 [-0]_补=0\; 000\, 0000 [−0]补=00000000
4 ------- 移码表示法 -------
在 X X X上增加一个偏移量定义,用于表示浮点数中的阶码。机器字长为 n n n,规定偏移量为 2 n − 1 2^{n-1} 2n−1
X X X为纯整数,则 [ X ] 移 = 2 n − 1 + X ( − 2 n − 1 ⩽ X < 2 n − 1 ) [X]_移=2^{n-1} + X(-2^{n-1}\leqslant X<2^{n-1}) [X]移=2n−1+X(−2n−1⩽X<2n−1)
X X X为纯小数,则 [ X ] 移 = 1 + X ( − 1 ⩽ X < 1 ) [X]_移=1 + X(-1\leqslant X<1) [X]移=1+X(−1⩽X<1) - 定点数和浮点数
1 -------定点数-------
小数点位置固定不变的数,一般是两种,定点整数(纯整数)和定点小数(纯小数)
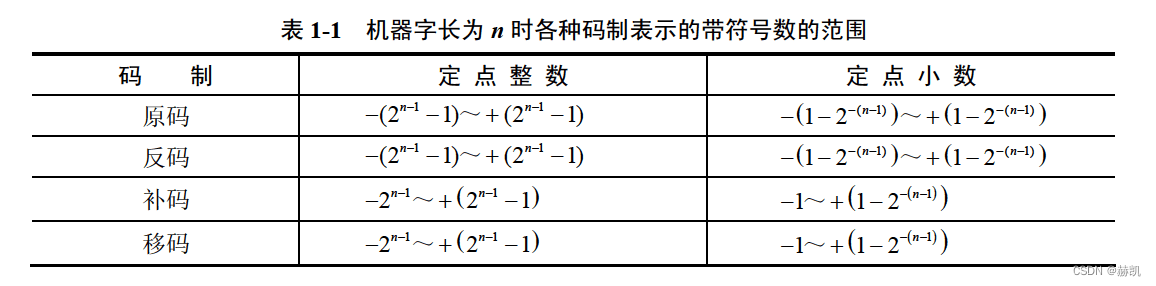
2 -------浮点数-------
一个二进制数字N可以表示为更一般的形式,那就是 N = 2 E ∗ F N=2^E*F N=2E∗F,其中E称为阶码,F称为尾数。用阶码和尾数表示的数为浮点数。表示格式为:
其中阶符是阶码的符号,数符是尾数的符号,也就是整个浮点数的符号。
由于一个数的浮点表示不固定,所以有了规格化表示,将尾数的绝对值限定在 [0.5,1] 。
3 -------IEEE 754-------
这个就是约定俗成的工业标准,标准形式如下:
( − 1 ) S 2 E ( b 0 b 1 b 2 b 3 . . . b p − 1 ) (-1)^S2^E(b_0b_1b_2b_3...b_{p-1}) (−1)S2E(b0b1b2b3...bp−1)
( − 1 ) S (-1)^S (−1)S为该浮点数的数符,S取1或0决定正或负; E E E为指数(阶码),使用移码表示的; ( b 0 b 1 b 2 b 3 . . . b p − 1 ) (b_0b_1b_2b_3...b_{p-1}) (b0b1b2b3...bp−1)为尾数,长度为 P P P位,用源码表示。
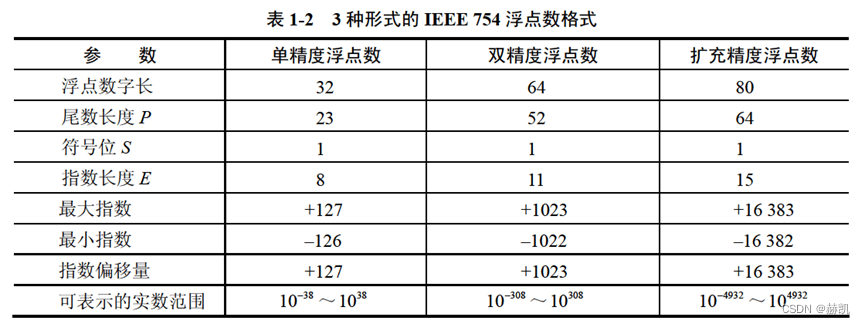
<1> 规格化的值
当阶码部分的二进制不全为0也不全为1,所表示的是规格化的值。
<2> 非规格化的值
当阶码部分的二进制值全为0,所表示的数是非规格化的。
<3> 特殊值
当阶码部分的二进制值全为1时,表示特殊的值。
4 -------浮点数的运算-------
<1> 对阶
<2> 求尾数和
<3> 结果规格化并判溢出
<4> 舍入处理
<5> 溢出判别
校验码
提高硬件电路的可靠性+提高代码的校验能力 ⇒ 校验码 ⇒ 合法编码 + 错误编码
码距,是指一个编码系统中任意合法编码之间至少有多少个二进制位不同。
合法编码用于传送数据,错误编码时不允许再数据中出现的编码。
- 奇偶校验码
通过在编码中增加一位校验位来使编码1的个数为奇数(奇校验)或者为偶数(偶校验),从而使码举距变为2。
奇偶校验码 = 水平奇偶校验码 + 垂直奇偶校验码 + 水平垂直校验码 - 海明码
利用就性来检错和纠错的校验方法。 - 循环冗余校验码
利用生成多项式为k个数据位产生r个校验位来进行编码,其编码长度位k+r
代码格式为

本文含有隐藏内容,请 开通VIP 后查看