实现 Alpha-Beta 剪枝
Alpha-Beta
Alpha-Beta 是在 MINIMAX 的基础上进行了剪枝操作,遍历的树更少,却也能得到相同的决策,在实现算法时候遇到了小坑,如下所示:

图 1 不同的伪代码 两个伪代码的不同处在于画红线的地方,在 mini 中对 alpha 的判断。经过手动推演+程序运行证明左边的代码是正确的。
遇到的问题:
alpha 和 beta 的定义
在最开始的时候没有完全理解算法的含义,将这两个变量全都定义成了全局变量,这也导致了之后判断的错误。因为虽然有时,顶层的 alpha 或 beta 和最底部的 alpha、 beta 值是一样的,但是他们并不是由于直接同步而相同的。在递归回溯的过程中,存在一个值一层层向上传递的过程,而在这个过程中就存在值修正的问题:你最开始得到的值并不就是最终的结果。并且在正常情况下,后续节点的 alpha 或 beta 将会和之前节点的进行比较,进行修正,而当设置全局变量后,后续节点直接就得到了 alpha 和 beta 的值,这样步骤颠倒势必会导致结果错误。
在顶层需要添加的 action 记录
当程序在 MIN 或者 MAX 层递归运行的时候,由于其目的只是找到最小值或最大值就可以了,因此照搬伪代码就。但是当到了 MAX 顶层的时候,需要进行 action 选择的决,决策的依据就是 alpha 最大值的选择。由于之前的代码只会评判出最大值是谁,而评判不出最大值在哪,因此需要在最顶层的时候有一个 action 的记录,即当更新得到更大的 alpha 的时候,同样也更新导致这个变化的 action。最终就可以返回这个 action 作为正确的选择路径了。
结果展示解决完上述问题后,就可以通过所有的测试了,结果展示如下图所示:
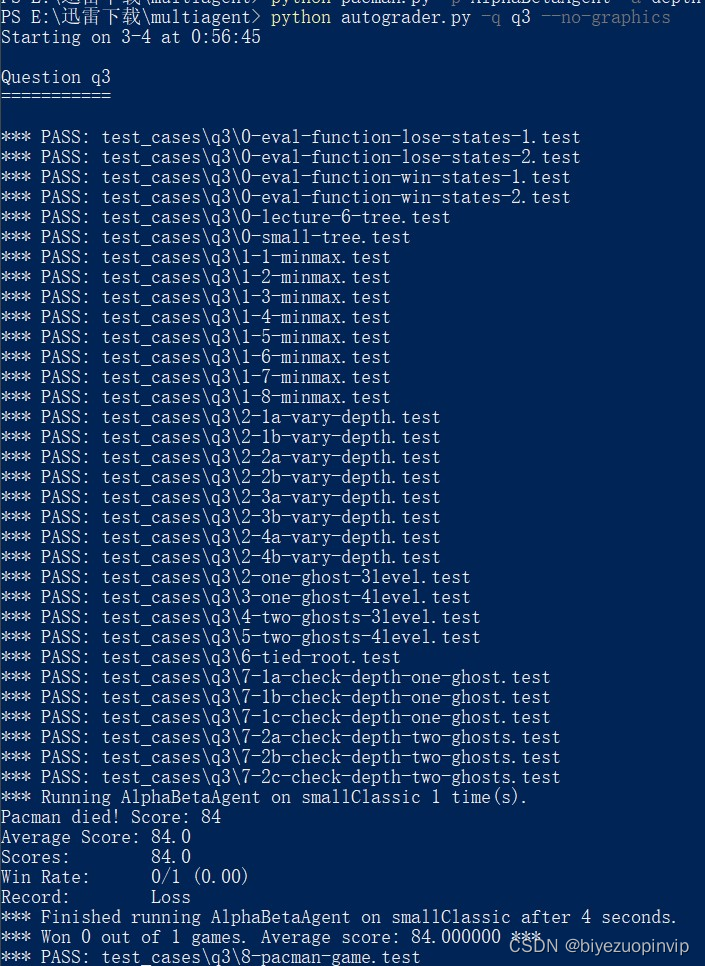
图 2 运行 python autograder.py -q q3 --no-graphics 的结果展示 最终运行的结果还是和上次一样,也确实,毕竟 Alpha-Beta 算法只是对 MINIMAX 进行剪枝,不会改变选择的结果。
算法时间比较 这里我直接用的 autograder 运行 q1 和 q2,来看运行时间的不同,结果如下:
图 3 q3 的运行时间
图 4 q2 的运行时间
从上图可以明显看到,使用 Alpha-Beta 的时候,运行时间只用了 1 秒,而运行 q2 的时候用了 2 秒…好吧,并不明显…主要是因为默认似乎都是两层递归的原因,如果需要加深一下层数就能能看到更明显的差异了。
尝试了一下使用递归层数为 5 层的两种算法,差异立刻就体现出来了,在使用 AlphaBeta 的时候,能以肉眼可见的速度进行移动,到了 Minimax 的时候,等他动一步的时间可以泡杯茶了…由此可见算法速度着实提升了。

图 5 使用深度 5 来测试两种算法