麻省理工学院 - MIT - 线性代数（我愿称之为线性代数教程天花板）_哔哩哔哩_bilibili

一、子空间投影

投影（射影）

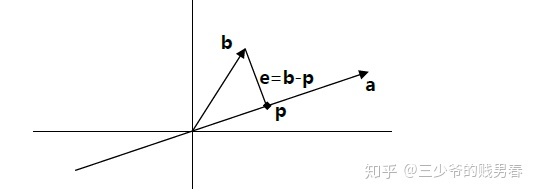
投影问题的几何解释就是：如何在向量a的方向上寻找与向量b距离最近的一点。

从图中可以看出，这个距离最近的点p就位于穿过b点并与向量a正交的直线与向量a所在直线的交点上。这就是b在a上的投影。如果我们将向量p视为b的一种近似，则长度e=b-p就是这一近似的误差。

(9条消息) 线性代数——理解向（2）_MUTA️的博客-CSDN博客

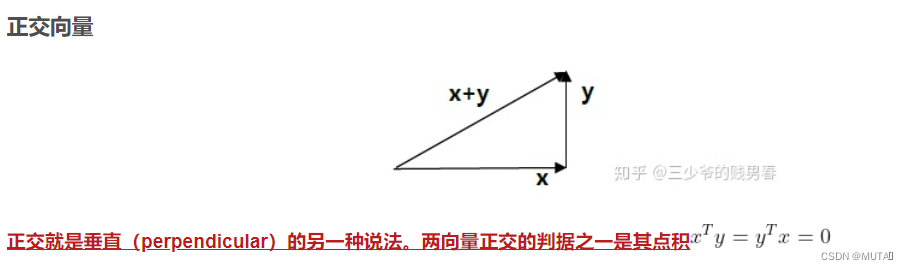
投影矩阵

我们将投影问题用投影矩阵的方式进行描述，即为p=Pb，其中P为投影矩阵。

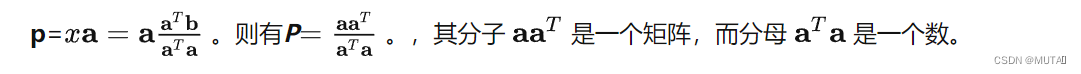
$P=A(A^{T}A)^{-1}A^{T}$ 当它作用于向量b，相当于把b投影到矩阵A的列空间。

(计算矩阵的除法，其实就是将被除的矩阵先转化为它的逆矩阵，它的逆矩阵相当于被除的矩阵分之一，那么矩阵的除法就相当于前面的矩阵和后面的矩阵的逆矩阵相乘的乘积)

观察这个矩阵可知，矩阵P的列空间就是向量a所在的直线，矩阵的秩是1？？？？

p是P的线性组合，所以p的列空间和P的列空间相同，又因为p和a共线，所以矩阵P的列空间就是向量a所在的直线，秩为1.

矩阵的秩是1。投影矩阵P是一个对称矩阵。另一方面，如果做两次投影则有 $P^{2}b=Pb$ ，这是因为第二次投影还在原来的位置。因此矩阵P有如下性质： $P^{2}=P$ ， $P^{T}=P$ 。

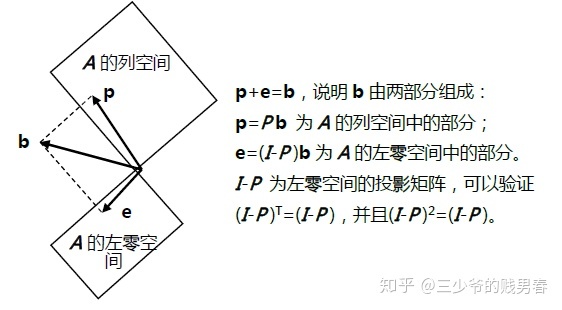
为什么要投影？

如前所述，方程Ax=b有可能无解，我们需要得到方程的“最优解”。这里的问题在于向量Ax一定在矩阵A的列空间之内，但是b不一定，因此我们希望将b投影到A的列空间得到p，将问题转化为求解 $A\hat{x}=p$ 。

最小二乘法

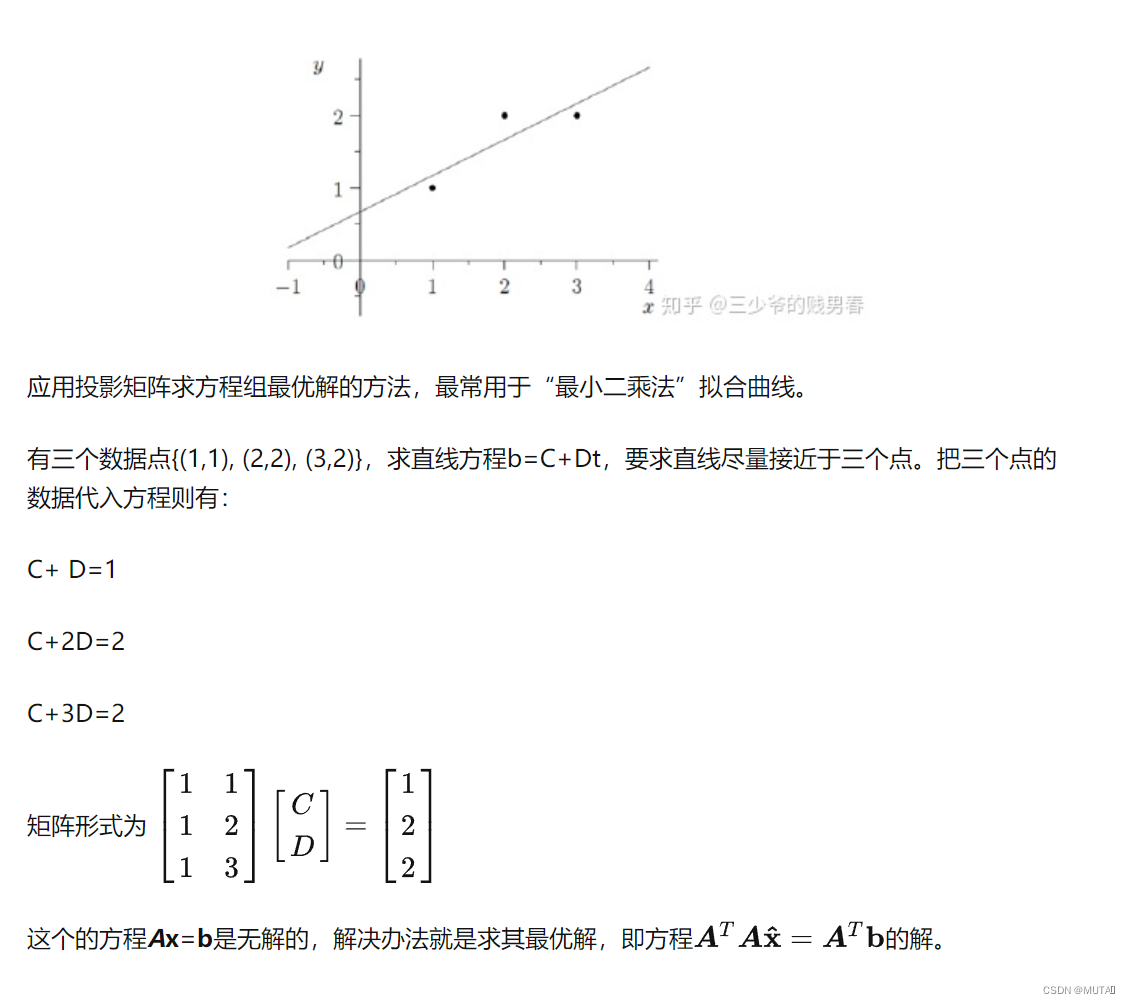
最优解的含义即为误差最小，这里误差就是每个方程误差值的平方和 $||e||^{2}=||Ax-b||^{2}$ ，因此就是寻找具有最小误差平方和的解x，这就是所谓的“最小二乘”问题。

从几何上讨论求解过程，就是试图寻找数据点到直线距离的平方和 $e_{1}^{^{2}}+e_{2}^{^{2}}+e_{3}^{^{2}}$ 最小的情况，此时得到的C+Dt分别为p1，p2和p3，它们是满足方程并最接近于b的结果。

另一种理解：对于R3空间上的向量b，它投影到矩阵A的列空间中会得到向量p=[p1 p2 p3]，投影到矩阵A的零空间中则为e。

求解 $\hat{x}=\begin{bmatrix} \hat{C}\\ \hat{D} \end{bmatrix}$ 和p：

方程 $A^{T}A\hat{x}=A^{T}b$ ,先计算 $A^{T}A$

$\begin{bmatrix} 1 &1 &1 \\ 1&2 &3 \end{bmatrix}\begin{bmatrix} 1 &1 \\ 1&2 \\ 1& 3 \end{bmatrix}=\begin{bmatrix} 3 &6 \\ 6& 14 \end{bmatrix}$

加上b做增广矩阵，因为左乘行向量相当于对行向量进行线性组合，所有加上b对结果不影响

$\begin{bmatrix} 1 &1 &1 \\ 1&2 &3 \end{bmatrix}\begin{bmatrix} 1 &1 &| 1\\ 1& 2 &|2 \\ 1& 3 &|2 \end{bmatrix}=\begin{bmatrix} 3 & 6 &|5 \\ 6& 14 & |11 \end{bmatrix}$

上述结果可理解为：

$\begin{bmatrix} 3 &6 \\ 6 &14 \end{bmatrix}\begin{bmatrix} \hat{C}\\ \hat{D} \end{bmatrix}=\begin{bmatrix} 5\\ 11 \end{bmatrix}$

解的 $\hat{C}=2/3,\hat{D}=1/2$

二、正交

标准正交

如果矩阵的列向量是相互垂直的单位向量，则他们一定是线性无关的，称这个向量为标准正交

上述条件可理解为任意向量q和其他q正交内积为0，和自身正交结果为1

标准正交矩阵

如果矩阵Q（可以不是方阵）的列向量为标准正交向量，则 $Q^{T}Q=T$ 为单位阵。

一个标准正交的方阵我们称之为“正交矩阵”。如果Q为方阵，因为 $Q^{T}Q=I$ ，所以 $Q^{T}=Q^{-1}$ 。

注意必须是方阵，必须是标准正交，而不只是正交。

标准正交列向量的优势

若Q的列向量为标准正交向量，则投影到Q的列空间的投影矩阵为： $P=Q(Q^{T}Q)^{-1}Q^{T}$ ,因为 $Q^{T}Q=I$ ，所以 $P=QQ^{T}$ ,这种情况会降低很多运算量。

如果Q为方阵，则P=I

很多复杂问题使用标准正交向量之后都变得简单。如果基为标准正交，则方程 $A^{T}A\hat{x}=A^{T}b$ 的解变为 $\hat{x}=Q^{T}b$ ， $\hat{x}$ 的分量 $\hat{x_{i}}$ 就等于 $q_{i}^{T}b$ 。

施密特正交化

从两个线性无关的向量a和b开始，它们张成了一个空间，我们的目标是希望找到两个标准正交的向量q1，q2能张成同样的空间。Schmidt给出的结论是如果我们有一组正交基A和B（注意这个小节A，B，C均为向量），那么我们令它们除以自己的长度就得到标准正交基：

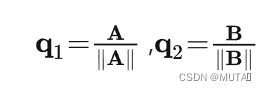
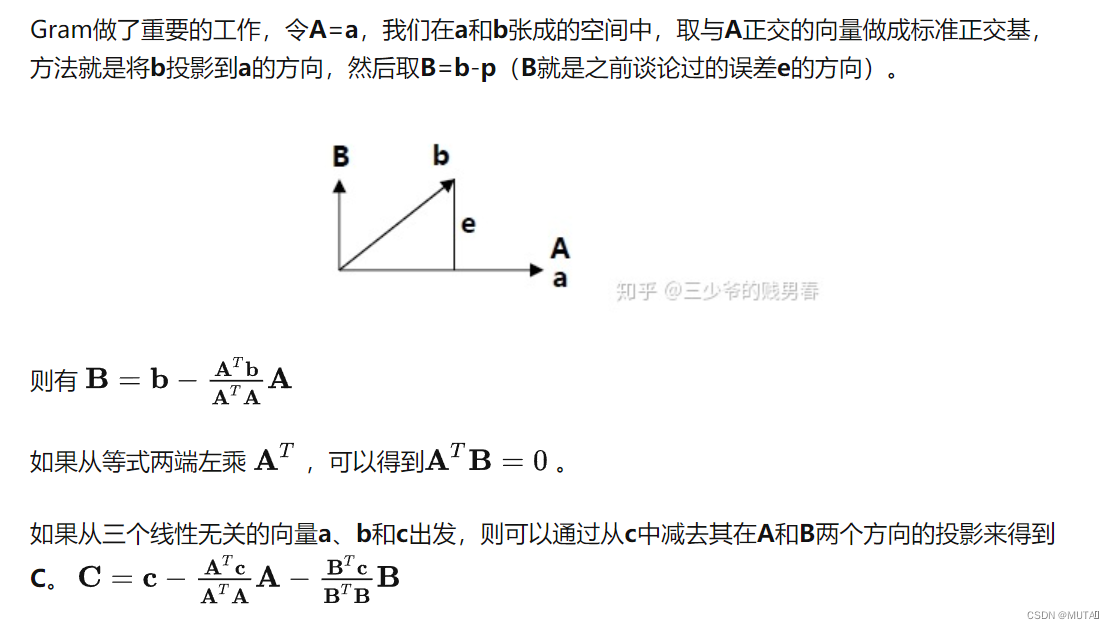
这里理解成三维空间，因为a，b，c三个向量线性无关

（注意上面正体加粗A代表向量，斜体A代表矩阵，只是用的同一字母，不要搞混。A=QR是参考消元矩阵A=LU列的同类型式子，不是推导得来的，而是根据这个式子以及各向量关系反向知道了R为上三角阵）

为什么要施密特正交？

如何理解施密特（Schmidt）正交化 - 知乎 (zhihu.com)

观看该链接里面视频有助理解

在一个平面，或者三维空间中，任意一点都可以被坐标系表示出来。而我们更喜欢的是单位直角坐标系，因为在一个单位直角坐标系中，任意一个向量的坐标分量，通过简单的投影就可以搞定。因此，如何找到欧式空间的一个“直角坐标系”，变得非常重要。 施密特正交化法就告诉我们了一种把“任意坐标系”变为“直角坐标系”的方法。

加深对施密特正交理解观看下列习题视频

18 Gram-Schmidt正交化_哔哩哔哩_bilibili

线性代数——理解向(3)