⭐️前面的话⭐️

本篇文章介绍来自牛客试题广场的两道题题解，分别为【星际密码】和【数根】，展示语言java。

小贴士：本专栏所有题目来自牛客->面试刷题必用工具

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2022年8月30日🌴
✉️坚持和努力一定能换来诗与远方！
💭推荐书籍：📚《算法》，📚《算法导论》
💬推荐在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

注意事项：本专栏所有题目都来自牛客网，如果有小伙伴还没有注册牛客，可以点击下方链接进行注册，注册完就能立即刷题了。不仅是刷题，上面还有很多有关就业的面经，面试题库，以及名企的模拟面试，我非常推荐它，博主自己用的也很多，也刷了不少题了！下图可以作证：

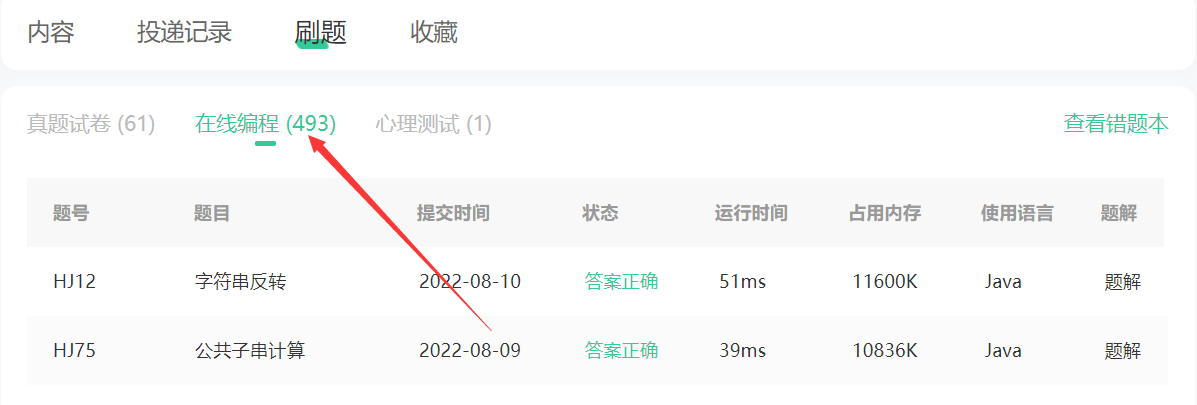
注册地址：牛客网

有关任何问题都可以与博主交流，你可以在评论区留言，也可以私信我，更可以加上博主的vx与博主一对一交流（文章最下方有）。

⭐️星际密码⭐️

🔐题目详情

星际战争开展了100年之后，NowCoder终于破译了外星人的密码！他们的密码是一串整数，通过一张表里的信息映射成最终4位密码。表的规则是：n对应的值是矩阵X的n次方的左上角，如果这个数不足4位则用0填充，如果大于4位的则只输出最后4位。
|1 1|^n => |Xn …|
|1 0| |… …|
例如n=2时，
|1 1|^2 => |1 1| * |1 1| => |2 1|
|1 0| |1 0| |1 0| |1 1|
即2对应的数是“0002”。

输入描述:

输入有多组数据。
每组数据两行：第一行包含一个整数n (1≤n≤100)；第二行包含n个正整数Xi (1≤Xi≤10000)

输出描述:

对应每一组输入，输出一行相应的密码。

输入

6
18 15 21 13 25 27
5
1 10 100 1000 10000

输出

418109877711037713937811
00010089410135017501

题目链接：星际密码

💡解题思路

基本思路： 数学计算找规律

解题思路：

首先这道题需要计算矩阵的n次方，需要使用到矩阵的乘法，所以我们首先将矩阵的乘法公式列出来：

$$\left(\begin{array}{cc}{C}_0& C_1\\ C_2& C_3\end{array}\right)=\left(\begin{array}{cc}{A}_0& A_1\\ A_2& A_3\end{array}\right)\ast \left(\begin{array}{cc}{B}_0& B_1\\ B_2& B_3\end{array}\right)=\left(\begin{array}{cc}{A}_0\times B_0+A_1\times B_2& A_0\times B_1+A_1\times B_3\\ A_2\times B_0+A_3\times B_2& A_2\times B_1+A_3\times B_3\end{array}\right)$$

然后我们按照此公式，对题目中的矩阵进行n次方，我们来观察规律：
$$\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)\ast \left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}2& 1\\ 1& 1\end{array}\right)$$

$$\left(\begin{array}{cc}2& 1\\ 1& 1\end{array}\right)\ast \left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}3& 2\\ 2& 1\end{array}\right)$$

$$\left(\begin{array}{cc}3& 2\\ 2& 1\end{array}\right)\ast \left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}5& 3\\ 3& 1\end{array}\right)$$

$$\left(\begin{array}{cc}5& 3\\ 3& 1\end{array}\right)\ast \left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}8& 5\\ 4& 1\end{array}\right)$$

$$\left(\begin{array}{cc}8& 5\\ 4& 1\end{array}\right)\ast \left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}13& 8\\ 5& 1\end{array}\right)$$

后面我就不再列举了，发现一个规律，就是左上角的那个元素的变化为从1开始的一个斐波拉契数列，所以我们可以通过这个规律直接先构造一个从1开始的斐波拉契数列，所以题目所给矩阵的n次方就相当于构造斐波拉契数列的第n项。

由于密码是四位数的，所以当数字大小不足四位数时我们需要补零，然后将密码不换行输出就行。

🔑源代码

// write your code here
import java.util.*;

public class Main {
    private static int[] data = new int[10001];
    private static void init() {
        data[1] = 1;
        data[2] = 2;
        for (int i = 3; i <= 10000; i++) {
            data[i] = (data[i - 1] + data[i - 2]) % 10000;
        }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        init();
        while (sc.hasNext()) {
            int n = sc.nextInt();
            for (int i = 0; i < n; i++) {
                int cur = sc.nextInt();
                StringBuilder sb = new StringBuilder();
                int num = data[cur];
                if (num < 10) sb.append("000");
                else if (num < 100) sb.append("00");
                else if (num < 1000) sb.append("0");
                
                sb.append(num);
                System.out.print(sb);
            }
            System.out.println();
        }
    }
}

🌱总结

本题有点脑经急转弯的感觉，需要使用到线性代数中矩阵乘法的知识对矩阵计算，然后通过计算结果推导出斐波拉契数列就简单了。

⭐️数根⭐️

🔐题目详情

数根可以通过把一个数的各个位上的数字加起来得到。如果得到的数是一位数，那么这个数就是数根；如果结果是两位数或者包括更多位的数字，那么再把这些数字加起来。如此进行下去，直到得到是一位数为止。
比如，对于24 来说，把2 和4 相加得到6，由于6 是一位数，因此6 是24 的数根。
再比如39，把3 和9 加起来得到12，由于12 不是一位数，因此还得把1 和2 加起来，最后得到3，这是一个一位数，因此3 是39 的数根。
现在给你一个正整数，输出它的数根。

输入描述:

输入包含多组数据。

每组数据数据包含一个正整数n（1≤n≤10E1000）。

输出描述:

对应每一组数据，输出该正整数的数根。

输入

24
39

输出

6
3

题目链接：树根

💡解题思路

基本思路： 模拟

解题思路：
由于题目的输入案例可能会有超过long数据访问的数字出现，因此我们需要将输入的数字以字符串的形式存储，然后先将字符串中所有的数字都加起来，得到的结果一定是一个int的值，最后再按照/10和%10的形式将一个大于10的数字拆分相加即可，直到最后结果小于10为止。

🔑源代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            String s = sc.next();
            char[] cs = s.toCharArray();
            int ans = 0;
            for (char c : cs) {
                ans += c - '0';
            }
            while (ans == 0 || ans >= 10) {
                int n = ans;
                ans = 0;
                while (n > 0) {
                    ans += n % 10;
                    n /= 10;
                }
            }
            System.out.println(ans);
        }
    }
}

🌱总结

本题为简单模拟题，按照题目模拟即可，唯一要注意的是就是题目给定的数据是很大的，需要使用字符串进行数字相加。

到文章最后，再来安利一下吧，博主也是经常使用，并且也经常在牛客上刷题，题库也非常丰富：牛客网，刷题，面试，内推都有。也欢迎与博主交流有关刷题，技术方面，以及与博主聊聊天，交个朋友也好啊，毕竟有朋自远方来！