I Rule90

1.代码编写

module top_module(
    input clk,
    input load,
    input [511:0] data,
    output [511:0] q ); 
    always@(posedge clk) begin
        if(load) 
            q <= data;
        else
            q <= {1'b0,q[511:1]}^{q[510:0],1'b0};
    end
endmodule

2.提交结果

Success

3.题目分析

Rule 90 is a one-dimensional cellular automaton with interesting properties.

The rules are simple. There is a one-dimensional array of cells (on or off). At each time step, the next state of each cell is the XOR of the cell’s two current neighbours. A more verbose way of expressing this rule is the following table, where a cell’s next state is a function of itself and its two neighbours:

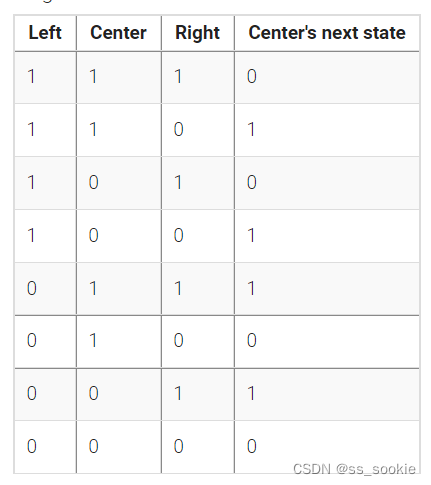
(The name “Rule 90” comes from reading the “next state” column: 01011010 is decimal 90.)

In this circuit, create a 512-cell system (q[511:0]), and advance by one time step each clock cycle. The load input indicates the state of the system should be loaded with data[511:0]. Assume the boundaries (q[-1] and q[512]) are both zero (off).

II Rule110

1.代码编写

module top_module(
    input clk,
    input load,
    input [511:0] data,
    output [511:0] q
);  
    always@(posedge clk) begin
        if(load)
            q <= data;
        else 
            q <= q&~{q[510:0],1'b0}|{1'b0,q[511:1]}&~q&{q[510:0],1'b0}|~{1'b0,q[511:1]}&{q[510:0],1'b0};
    end
endmodule

2.提交结果

Success

3.题目分析

Rule 110 is a one-dimensional cellular automaton with interesting properties (such as being Turing-complete).

There is a one-dimensional array of cells (on or off). At each time step, the state of each cell changes. In Rule 110, the next state of each cell depends only on itself and its two neighbours, according to the following table:

(The name “Rule 110” comes from reading the “next state” column: 01101110 is decimal 110.)

In this circuit, create a 512-cell system (q[511:0]), and advance by one time step each clock cycle. The load input indicates the state of the system should be loaded with data[511:0]. Assume the boundaries (q[-1] and q[512]) are both zero (off).

III Conway’s Game of life 16*16

1.代码编写

module top_module(
    input clk,
    input load,
    input [255:0] data,
    output [255:0] q ); 
    reg [17:0] d2 [17:0]; // high to low
    reg [2:0] sum;
    always@(*) begin
        integer row;
         // 索引 先行后列
        d2[0] = {q[240],q[255:240],q[255]};// 
        d2[17] = {q[0],q[15:0],q[15]};// 
        for(row=0;row<=15;row++) begin
            d2[row+1]={q[row*16],q[row*16+:16],q[row*16+15]};// row 1~16 q[row*16],q[(row*16+15)-:16],q[row*16+15]
        end        
    end
    always@(posedge clk) begin
        if(load)
            q <= data;
        else begin
            integer row2,col2;
            for(row2=1;row2<=16;row2++) begin
                for(col2=1;col2<=16;col2++) begin                
                	sum = d2[row2-1][col2]+d2[row2-1][col2-1]+d2[row2-1][col2+1]+d2[row2+1][col2]+d2[row2+1][col2-1]+d2[row2+1][col2+1]+d2[row2][col2+1]+d2[row2][col2-1]; // 这里一定要用阻塞赋值而非非阻塞赋值，原因在 题目分析 里。
                	case(sum)
                    	// 0-1 neighbour: Cell becomes 0.
						// 2 neighbours: Cell state does not change.
						// 3 neighbours: Cell becomes 1.
						// 4+ neighbours: Cell becomes 0.
                        3'b010: q[(row2-1)*16+col2-1] <= q[(row2-1)*16+col2-1];
                        3'b011: q[(row2-1)*16+col2-1] <= 1'b1;
                        default: q[(row2-1)*16+col2-1] <= 1'b0;
                    endcase
                end
            end
        end
    end
endmodule

2.提交结果

Success

3.题目分析

Conway’s Game of Life is a two-dimensional cellular automaton.

The “game” is played on a two-dimensional grid of cells, where each cell is either 1 (alive) or 0 (dead). At each time step, each cell changes state depending on how many neighbours it has:

• 0-1 neighbour: Cell becomes 0.

• 2 neighbours: Cell state does not change.

• 3 neighbours: Cell becomes 1.

• 4+ neighbours: Cell becomes 0.
  The game is formulated for an infinite grid. In this circuit, we will use a 16x16 grid. To make things more interesting, we will use a 16x16 toroid, where the sides wrap around to the other side of the grid. For example, the corner cell (0,0) has 8 neighbours: (15,1), (15,0), (15,15), (0,1), (0,15), (1,1), (1,0), and (1,15). The 16x16 grid is represented by a length 256 vector, where each row of 16 cells is represented by a sub-vector: q[15:0] is row 0, q[31:16] is row 1, etc. (This tool accepts SystemVerilog, so you may use 2D vectors if you wish.)

• load: Loads data into q at the next clock edge, for loading initial state.

• q: The 16x16 current state of the game, updated every clock cycle.
  The game state should advance by one timestep every clock cycle.

John Conway, mathematician and creator of the Game of Life cellular automaton, passed away from COVID-19 on April 11, 2020.

$sum需要用阻塞赋值，否则在第一个时钟周期内，更新q的‘<=’右侧语句等于sum等于0的状态时的，在第一个时钟周期末，q更新为此状态，并开始依次计算下一个sum，sum才刚刚更新为正确的状态，为时已晚。$