心电信号降噪方法分析
(1)基线漂移的常用滤除法是拟合基线抵消法,此法先估计或提取信号基线,然后进行减法运算去掉信号中漂移成分,达到滤波的目的。抑制基线漂移的另一种方法是采用线性相位滤波器,因为基线漂移的频带通常处于低频段。所以采用高通滤波器消除基线漂移,值得注意的是选择滤波器的阶数,阶次较高时,计算量较大,此外还有用基于神经网络设计的非线性自适应滤波器去除基线漂移影响的方法,这种滤波器容易受 QRS 组合波形变异的影响,算法复杂,计算工作量大。近年来,随着小波变换及其在心电信号的数字化滤波中应用新技术的兴起,将小波分解与重构法应用到心电信号滤波去噪技术可以较好抑制信号中的基线漂移,可以认为基线漂移相对集中,其主要成分在某子空间存在,如果抑制其能量,就能很好的去除基线漂移。
(2)对工频干扰抑制方法较多,主要有平滑滤波、简单整系数带阻滤波器、Levkov 滤波、自适应滤波器等。平滑滤波是较早人们所采用的数字化滤波方法,优点是算法简单,处理速度快,滤波效果较好,但其滤波通带窄,造成心电信号中的 QRS 波群削峰严重,信号衰减较大,因此使用该方法有局限性。简单整系数带阻滤波器填补了 IIR 滤波器计算量较大和 FIR 滤波器不能实现严格线性相位的缺点,它用 IIR 结构实现 FIR 滤波器功能,既保证计算量较少,又具有严格的线性相位特性。同时用较少次数递归运算实现非递归 FIR 滤波,减少运算需要的计算机,滤波效果较好,常用于信号实时处理。但滤波有很大延时,滤除的信号频率是固定的,在干扰产生波动时滤波效果下降明显。Levkov滤波法基本原理是先提取一个线性段,滤波后的值为这个线性段原始数据平均值,再算出工频干扰的幅度作为非线性段的噪声模板。对非线性段处理即用原始数据减去临近线性段得出的噪声模板值为真值。此方法算法简单,参数可调,运算量小,能适应干扰频率和幅度变化,滤波效果较好。自适应滤波器是一种能够根据输入信号自动调整自身性能并进行数字信号处理的数字滤波器,具有自学习和自调整能力。如果工频干扰的频率比较稳定,可以采用具有固定中心频率的窄带带阻滤波器(陷波器)来消除。在很多情况下,不易准确知道工频干扰的频率,同时工频干扰会存在一定的频率漂移,所以在心电信号分析处理中常采用自适应噪声抵消原理。在工频电源上取参考信号经降压变压器送入自适应滤波器,调节工频正弦信号的幅度和相位,使之与心电放大器输出的信号的误差信号达到最小,从而保证心电放大器输出中的工频干扰被抵消,而纯净心电信号保留下来。该方法运算速度快,算法也相对比较简单,但需要自学习过程估计噪声,不能跟踪干扰幅度变化。
鉴于此,采用小波分析等信号处理方法对心点信号进行降噪,运行环境为MATLAB 2018。
clc
clear all;
close all;
folderType = 'AF';
fileName = strcat('JS02677');
matFileName = strcat(fileName, '.mat');
heaFileName = strcat(fileName, '.hea');
data_path = fullfile('data/raw/', folderType, matFileName);
data = load(data_path);
ecg_orig = data.val(1, :);
ecg_orig(isinf(ecg_orig)|isnan(ecg_orig)) = 0;
fs = 125;
N = length(ecg_orig);
t = (0:N-1) / fs;
f = (0:N-1) * (fs / N);
frequencies = f(1:N/2+1);
%RESAMPLE SIGNAL To 125Hz
% [ecg, t] = resample_signal_125(ecg_orig, t_orig);
%Assigning new parameter
% fs = 125;
% N = length(ecg);
% f = (0:N-1) * (fs / N);
%Applying high pass and low pass filters
hl_filter = hpf_lpf(ecg_orig, fs);
pl_filter = powerline_removal(hl_filter, fs);
movSignal = moving_avg(pl_filter, 5);
waveletSignal = wavelet_denoise(movSignal, 5);
% Create a single figure with subplots for each signal
figure;
% Original ECG
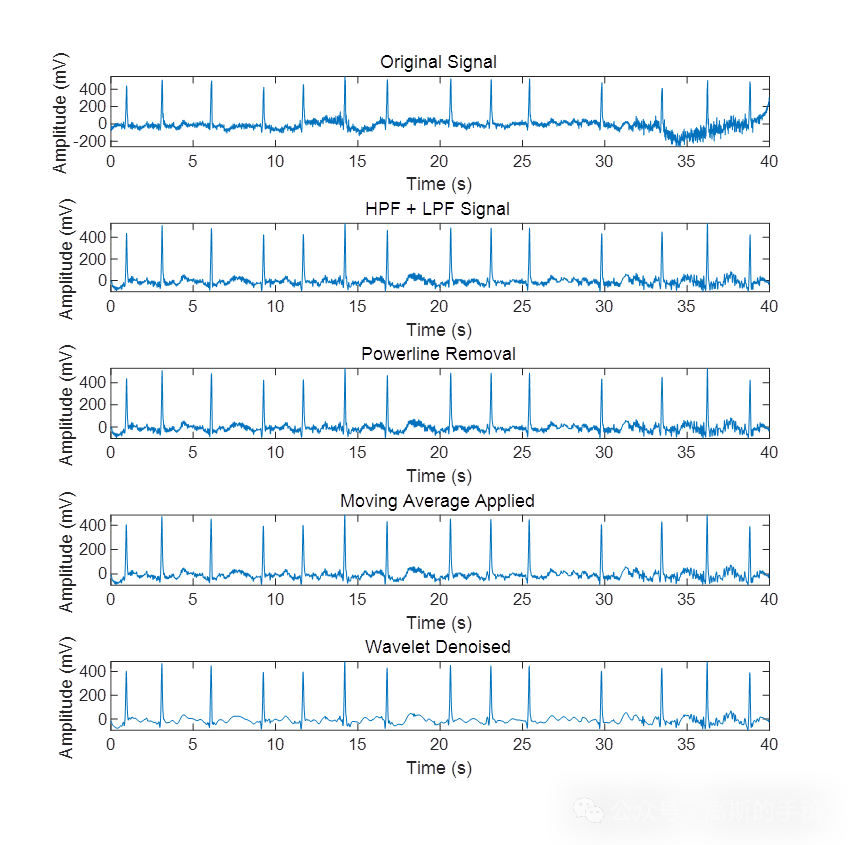
subplot(5, 1, 1);
plot(t, ecg_orig);
xlabel('Time (s)');
ylabel('Amplitude (mV)');
title('Original Signal');
% HPF + LPF Filtered
subplot(5, 1, 2);
plot(t, hl_filter);
xlabel('Time (s)');
ylabel('Amplitude (mV)');
title('HPF + LPF Signal');
% Powerline Removal
subplot(5, 1, 3);
plot(t, pl_filter);
xlabel('Time (s)');
ylabel('Amplitude (mV)');
title('Powerline Removal');
% Moving Average applied
subplot(5, 1, 4);
plot(t, movSignal);
xlabel('Time (s)');
ylabel('Amplitude (mV)');
title('Moving Average Applied');
% Wavelet Denoised
subplot(5, 1, 5);
plot(t, waveletSignal);
xlabel('Time (s)');
ylabel('Amplitude (mV)');
title('Wavelet Denoised');
out = waveletSignal;
figure
subplot(4, 1, 1);
[Pxx,F] = periodogram(ecg_orig,[],length(ecg_orig),fs);
plot(F,10*log10(Pxx))
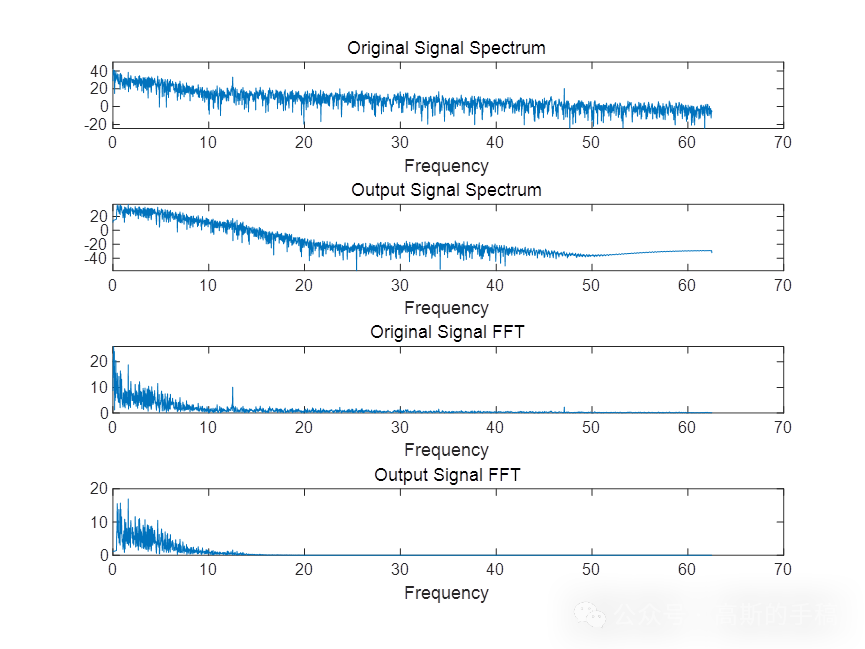
title('Original Signal Spectrum');
xlabel('Frequency');
subplot(4, 1, 2);
[Pxx_out,F_out] = periodogram(out,[],length(out),fs);
plot(F,10*log10(Pxx_out))
title('Output Signal Spectrum');
xlabel('Frequency');
subplot(4, 1, 3)
input_fft = fft(ecg_orig)/N;
input_fft = 2 * abs(input_fft(1:N/2+1));
plot(frequencies, input_fft)
title('Original Signal FFT');
xlabel('Frequency');
subplot(4, 1, 4)
output_fft = fft(out)/N;
output_fft = 2 * abs(output_fft(1:N/2+1));
plot(frequencies, output_fft)
title('Output Signal FFT');
xlabel('Frequency');
output_folder_path = fullfile('data/processed/', folderType);
if ~exist(output_folder_path, 'dir')
mkdir(output_folder_path);
end
output_path = fullfile('data/processed/', folderType, matFileName);
完整数据和代码通过知乎学术咨询获得:https://www.zhihu.com/consult/people/792359672131756032?isMe=1
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。