【凸优化第一章】凸集

发布于：2024-10-15 ⋅ 阅读:(115) ⋅ 点赞:(0)

一、三种集合

1.0（补充）直线与线段

定义

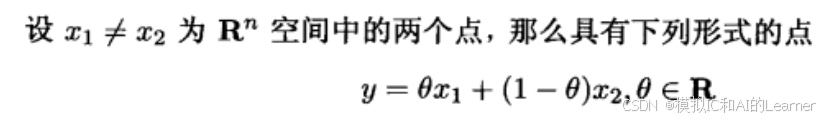
$\theta \epsilon R$ 时为直线， $\theta \epsilon [0,1]$ 时为线段。

扩展：

$x1$ ， $x2$ ， $x3$ 为 $R^{n}$ 空间中的不共线的三个点，那么对于 $y=\theta _{1}x_{1}+\theta _{2}x_{2}+\theta _{3}x_{3}$ ，其中 $\theta _{1}+\theta _{2}+\theta _{3}=1$ .

当仅满足条件 $\theta _{1}+\theta _{2}+\theta _{3}=1$ 而对 $\theta$ 没有其他限制时， $y$ 是过 $x1$ ， $x2$ ， $x3$ 三点无限延申的平面，当对 $\theta$ 加一个条件 $\theta \epsilon [0,1]$ 时，y为 $x1$ ， $x2$ ， $x3$ 三点连线形成的三角区域。

1.1仿射集

1.1.1仿射集

1.1.1.1定义：

1.1.1.2自我理解为：

（1）仿射集：

集合中任意点之间组成向量张成的空间即是这个集合。举个例子，一维情况下只有直线是仿射集（至少两个点确定），二维情况下只有无限延申的平面是仿射集（至少三个点确定），三维情况下只有整个三维空间是仿射集（至少四个点确定）。

（2）仿射集与向量空间：

当不再限制 $\theta _{1}+\theta _{2}+\cdot \cdot \cdot +\theta _{k}=1$ 时， $y=\theta _{1}x_{1}+\theta _{2}x_{2}+\cdot \cdot \cdot +\theta _{k}x_{k}$ 表示的集合将是向量 $x_{1}$ ， $x_{2}$ ，...， $x_{k}$ 张成的空间，当包含 $x_{1}$ ， $x_{2}$ ，...， $x_{k}$ 的仿射集不经过原点时，这些点张成的向量空间比包含它们的仿射空间高一维，当包含 $x_{1}$ ， $x_{2}$ ，...， $x_{k}$ 的仿射集经过原点时，仿射集与向量空间等同。几个点线性组合张成的向量空间默认包含了原点，相当于多一点，而仿射空间没有原点，所以同一组点线性组合构成的线性空间比仿射空间多一维。

（3）仿射空间：

一个仿射集是一个仿射空间，它与向量空间的区别是，向量空间一定包含原点（零向量），而仿射空间可以不包含原点，仿射空间C和向量空间V之间的关系可以表示为C=V+x0 。（C、V、x0是更高维空间的元素，x0为向量，其在仿射空间中，等式的意义是仿射空间C是向量空间沿x0方向平移|x0|的距离，可能脱离原点。）。若有仿射空间C，则C-x0为向量空间（x0为仿射空间中任意一点）

1.1.3仿射组合与仿射包

1.1.3.1仿射组合

如果 $\theta _{1}+\cdot \cdot \cdot +\theta _{k}=1$ ，则称 $\theta _{1}x_{1}+\theta _{2}x_{2}+\cdot \cdot \cdot +\theta _{k}x_{k}$ 为 $x_{1}$ ， $x_{2}$ ，...， $x_{k}$ 的仿射组合。

1.1.3.2仿射包

自我理解：当C是仿射集合是，它的仿射包是它本身；当C不是仿射集合是，它的发生包为C中所有点构成的空间（即，C中两个点的话它的仿射包就是过两点的直线，C中若是不共线的三个点的话它的仿射包就是过三个点的无限延申的平面，依次类推）。

1.2凸集

1.2.1凸集

1.2.1.1定义：

标准的定义太过枯燥，下面更直观解释：

如果集合中的每一点都可以被其他点沿着它们之间一条无阻碍的路径看见，那么这个集合就是凸集。所谓无阻碍，是指整条路径都在集合中。

仿射集包含穿过集合中任意不同两点的整条直线，任意不同两点间的线段自然也在集合中。因而仿射集是凸集。

1.2.1.2例子：

第一个是凸集，第二、三个不是凸集。

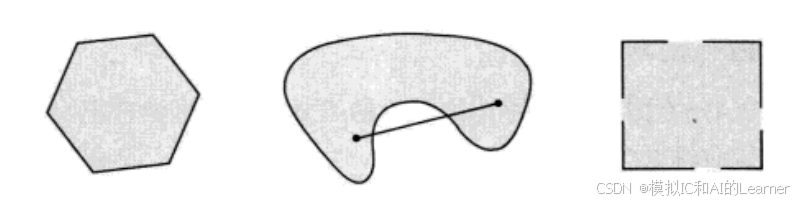
1.2.3凸组合与凸包

1.2.3.1凸组合

当对 $\sum \theta _{i}$ 进行限制即 $\sum \theta _{i}=1$ ，且 $\theta _{i}\geqslant 0$ 时（这个限制说明所有的 $\theta _{i}$ 都不超过1且为正数），上面的凸组合就是线段。

1.2.3.2凸包

集合的所有凸组合组成的集合是其凸包。

自我理解：

凸集的凸包是其本身，非凸集的凸包为包含这个集合的最小凸集。

例子：

1.3锥集

1.3.1锥集

1.3.1.1定义

1.3.1.2直观理解

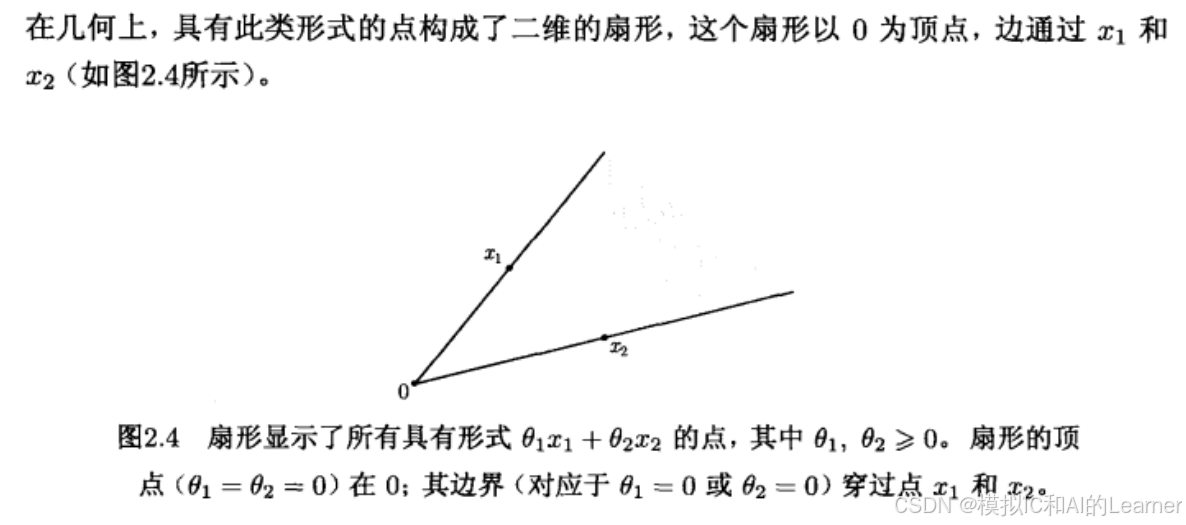
一个点构成的锥集为射线，两个点构成的锥集为扇形辐射区域。

1.3.2锥组合与锥包

1.3.2.1锥组合

1.3.2.2锥包

自我理解：锥集的锥包为其本身，非锥集的锥包为包含这个集合的最小锥集。

1.4三种集合辨析（自我理解）

1.4.1二维举例

二维情况下，两个点 $x_{1}$ ， $x_{2}$ 构成的集合

（1）仿射包为过两点的直线，其是包含两点的最小仿射集

（2）凸包为过两点的线段，其是包含两点的最小凸集

（3）锥包为从原点到过两点的辐射扇形区域，其是包含两点的最小锥集

（4）补充：包含两点的最小向量空间是从原点到两个点的向量张成的整个二维平面

1.4.2三维举例

三维情况下，两个点 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 构成的集合

（1）仿射包为过三点的平面，其是包含三点的最小仿射集

（2）凸包为过三点的三角形平面区域，其是包含三点的最小凸集

（3）锥包为从原点到过三点的辐射三角扇形区域，其是包含三点的最小锥集

（4）补充：包含三点的最小向量空间是从原点到三个点的向量张成的整个三维空间

1.4.3三者的联系与差别

1.4.3.1仿射集、凸集、锥集的包含关系：

（1）仿射集一定是凸集

（2）锥集一定是凸集

1.4.3.2三者差别

三者并不是那么相似，更准确地说，

（1）仿射集和凸集地联系很紧密，而它们与锥集有很大地区别，仿射集和凸集仅形成过程中对参数 $\theta _{i}$ 的约束强度不同，凸集形成过程中对它的约束更强。

（2）我认为锥集与向量空间地联系更为紧密，锥集是向量空间张成过程中对线性组合的参数加上 $\theta _{i}\geqslant 0$ 的约束，由同样的一组基形成的锥集和向量空间，锥集是向量空间的子集。