动态规划·区间DP

目录

石子合并 

涂色

制作回文串

 环形区间DP

能量项链 

石子合并 

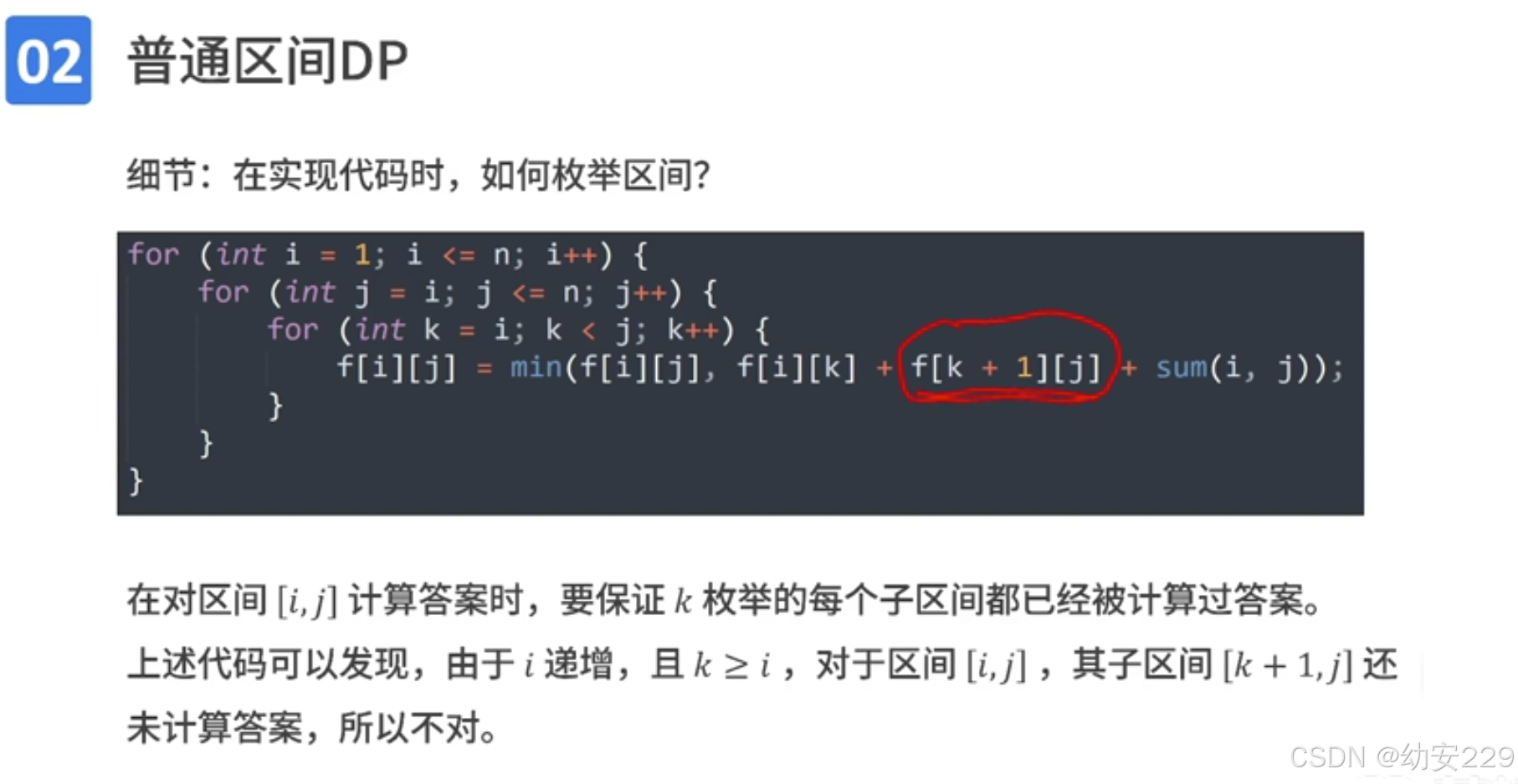
枚举区间是从小到大去枚举的 ，例如，一开始i是2，那么就会枚举所有区间长度为2的区间，那么在计算区间长度为3的区间时，它的长度为2的子区间就一定是已经被计算过的了

这样就确保了对于一个区间[i,j]，它的所有的子区间都是已经被计算过的了

#include <bits/stdc++.h>
using namespace std;

const int N = 210;

int n;
int a[N],f[N][N];

int main()
{
  cin >> n;
  memset(f,127,sizeof f);
  for (int i = 1;i <= n;i++)
  {
    cin >> a[i];
    f[i][i] = 0;
    a[i] += a[i-1];
  }

  for (int len = 2;len <= n;len++)
  {
    for (int i = 1;i <= n - len + 1;i++)
    {
      int j = i + len - 1;
      for (int k = i;k < j;k++)
      {
        f[i][j] = min(f[i][j],f[i][k]+f[k+1][j]+a[j]-a[i-1]);
      }
    }
  }

  cout << f[1][n] << endl;
  return 0;
}

涂色

分析：

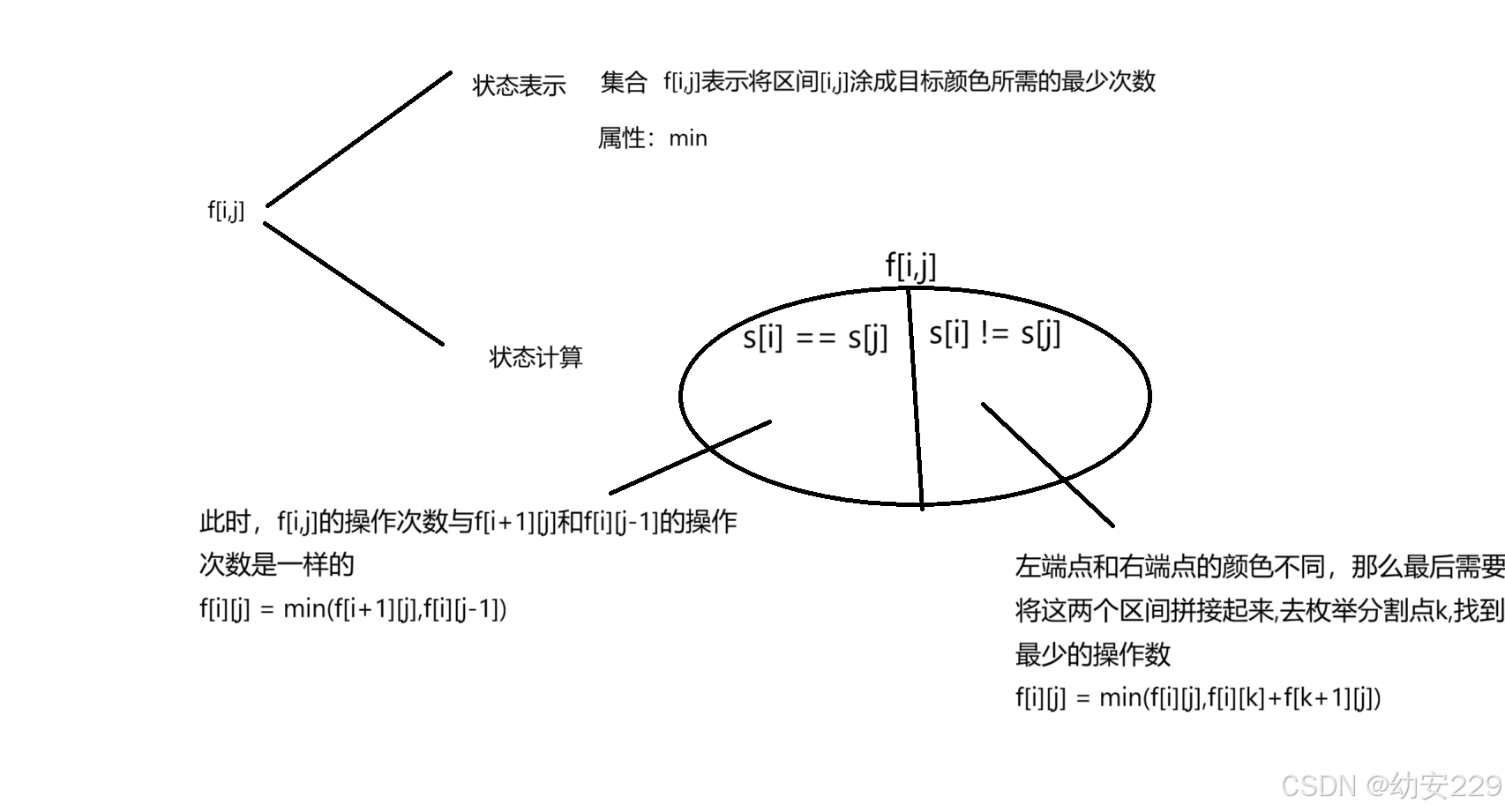
对于整个字符串，我们可以考虑把它拆分成若干份子区间

对于相邻的两个区间，例如，字符串长度为5，我们可以先考虑把[1,4]区间进行涂色，将对[5,5]进行涂色，这两个区间的操作次数之和就是整个木板的操作次数，也就是说我们可以通过合并两个相邻的子区间得到整个区间，那么我们可以考虑用区间dp来做这道题

#include <bits/stdc++.h>
using namespace std;

const int N = 55;

string s;
int f[N][N]; //f[i][j]表示区间[i,j]涂成目标颜色的最少次数

int main()
{
  cin >> s;
  int n = s.size();
  memset(f,127,sizeof f);
  for (int i = 0;i < n;i++) f[i][i] = 1;
  
  for (int len = 2;len <= n;len++)
  {
    for (int i = 0;i + len - 1 < n;i++)
    {
      int j = i + len - 1;
      if (s[i] == s[j])
      {
        f[i][j] = min(f[i+1][j],f[i][j-1]);
      }else {
        for (int k = i;k < j;k++)
        {
          f[i][j] = min(f[i][j],f[i][k]+f[k+1][j]);
        }
      }
    }
  }

  cout << f[0][n-1] << '\n';
  return 0;
}

制作回文串

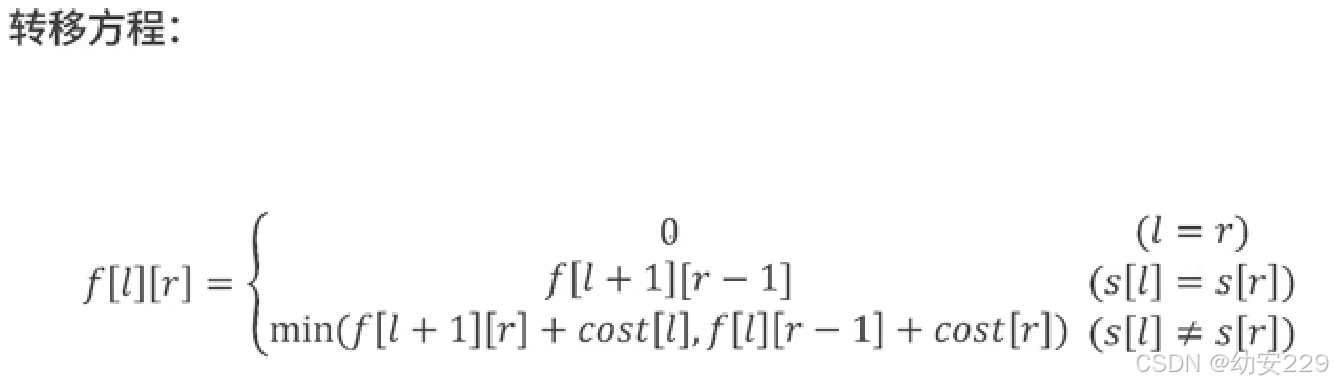
#include <bits/stdc++.h>
using namespace std;

const int N = 2010;

int n,m;
string s;
int w1[30],w2[30];
int f[N][N];

int main()
{
  cin >> m >> n >> s;
  for (int i = 1;i <= m;i++)
  {
    char ch;
    cin >> ch;
    cin >> w1[ch - 'a'] >> w2[ch - 'a'];
  }

  for (int len = 2;len <= n;len++)
  {
    for (int i = 0;i + len - 1 < n;i++)
    {
      int j = i + len - 1;
      if (s[i] == s[j])
      {
        if (len == 2)
        {
          f[i][j] = 0;
        }else{
          f[i][j] = f[i+1][j-1];
        }
        
      }else {
        f[i][j] = min(f[i+1][j] + min(w1[s[i] - 'a'],w2[s[i]-'a']),
        f[i][j-1] + min(w1[s[j] - 'a'] , w2[s[j] - 'a']));
      }
    }
  }

  cout << f[0][n-1] << '\n';
  return 0;
}

 环形区间DP

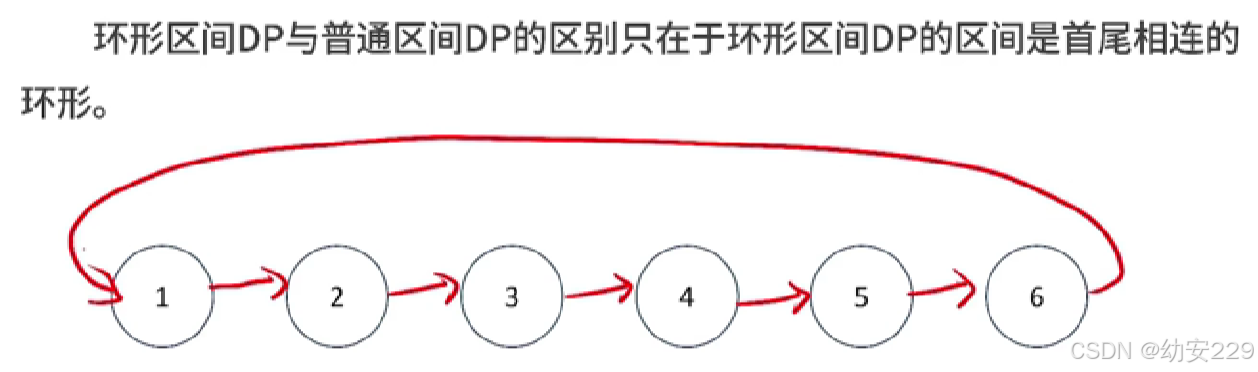
能量项链 

#include <bits/stdc++.h>
using namespace std;

const int N = 110;

int n;
int v[2*N];
int f[2*N][2*N];

int main()
{
  cin >> n;
  for (int i = 1;i <= n;i++)
  {
    cin >> v[i];
    v[i + n] = v[i];
  }

  for (int len = 2;len <= n;len++)
  {
    for (int i = 1;i + len - 1 <= 2*n;i++)
    {
      int j = i + len - 1;
      for (int k = i;k < j;k++)
      {
        f[i][j] = max(f[i][j],f[i][k] + f[k+1][j] + v[i]*v[k+1]*v[j+1]);
      }
    }
  }

  int ans = 0;

  for (int i = 1;i <= n;i++)
  {
    ans = max(ans,f[i][i+n-1]);
  }

  cout << ans << '\n';
  return 0;
}