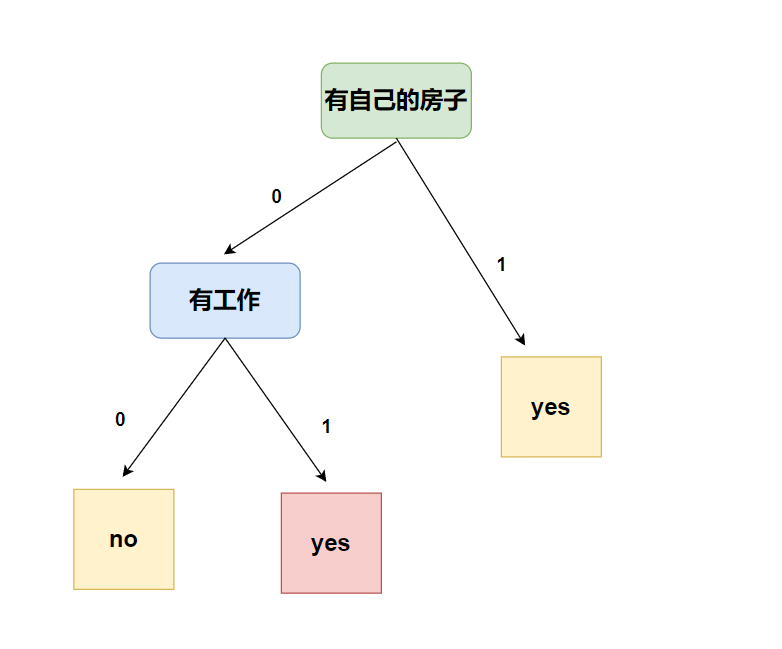
决策树是一种分类和回归方法,是基于各种情况发生的所需条件构成决策树,以实现期望最大化的一种图解法。
熵(entropy)是表示随机变量不确定性的度量,熵越大,随机变量的不确定性就越大:
H ( p ) = − ∑ i = 1 n p i l o g p i H(p) = - \sum_{i=1}^n p_ilogp_i H(p)=−i=1∑npilogpi
条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)表示在已知随机变量 X X X的条件下随机变量 Y Y Y的不确定性:
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X) = \sum_{i=1}^n p_iH(Y|X=x_i) H(Y∣X)=i=1∑npiH(Y∣X=xi)
当熵和条件熵中的概率有数据估计得到时,所对应的熵与条件熵分别称为经验熵和经验条件熵。
信息增益(information gain)表示得知特征X的信息而使得类Y的信息不确定性减少的程度。
g ( X , Y ) = H ( Y ) − H ( Y ∣ X ) g(X,Y) = H(Y) - H(Y|X) g(X,Y)=H(Y)−H(Y∣X)
决策树学习应用信息增益准则选择特征。给定训练数据集D和特征A,经验熵H(D)表示对数据集D进行分类的不确定性;经验条件熵H(D|A)表示在特征A给定条件下对数据集D进行分类的不确定性。它们的差即为信息增益。
根据信息增益准则的特征选择方法是:对训练数据集D,计算其每个特征的信息增益,权责信息增益最大的特征。
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征。使用信息增益比可以对此问题进行矫正。特征A对训练数据集D的信息增益比定义为其信息增益比 g ( D , A ) g(D,A) g(D,A)于训练数据集D关于特征A的值的熵 H A ( D ) H_A(D) HA(D)之比:
g R ( D , A ) = g ( D , A ) H A ( D ) g_R(D,A) = \frac {g(D,A)} {H_A(D)} gR(D,A)=HA(D)g(D,A)
H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ l o g 2 ∣ D i ∣ ∣ D ∣ H_A(D) = - \sum_{i=1}^n{\frac {|D_i|} {|D|} log_2 \frac {|D_i|} {|D|}} HA(D)=−i=1∑n∣D∣∣Di∣log2∣D∣∣Di∣
| 算法名称 | 特征选择准则 |
|---|---|
| ID3 | 信息增益 |
| C4.5 | 信息增益比 |
代码实现
数据处理:
def create_dataset():
"""
创建数据集
:return: 数据集和标签
"""
dataset = [
[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no'],
]
labels = ['年龄', '有工作', '有自己的房子', '信贷情况']
return dataset, labels
通过递归的方式实现ID3决策树算法:
from data_processing import create_dataset
import math
def createTree(dataset: list, labels: list, feature_labels: list):
"""
创建决策树
:param dataset: 数据集
:param labels: 标签
:param feature_labels: 已选择的特征标签
:return: 决策树
"""
class_list = [example[-1] for example in dataset]
# 如果所有类标签相同,则返回该类标签
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
# 如果数据集中只有一个特征,返回出现次数最多的类标签
if len(dataset[0]) == 1:
return majority_count(class_list)
# 选择最佳特征
best_feature = choose_best_feature_to_split(dataset)
best_feature_label = labels[best_feature]
feature_labels.append(best_feature_label)
# 创建决策树
my_tree = {best_feature_label: {}}
# 删除已选择的特征
del labels[best_feature]
feature_values = [example[best_feature] for example in dataset]
unique_values = set(feature_values)
for value in unique_values:
sub_labels = labels[:]
my_tree[best_feature_label][value] = createTree(split_dataset(dataset, best_feature, value), sub_labels, feature_labels)
return my_tree
def majority_count(class_list: list):
"""
返回出现次数最多的类标签
:param class_list: 类标签列表
:return: 出现次数最多的类标签
"""
class_count = {}
for vote in class_list:
if vote not in class_count.keys():
class_count[vote] = 0
class_count[vote] += 1
sorted_class_count = sorted(class_count.items(), key=lambda x: x[1], reverse=True)
return sorted_class_count[0][0]
def choose_best_feature_to_split(dataset: list):
"""
选择最佳特征
:param dataset: 数据集
:return: 最佳特征的索引
"""
num_features = len(dataset[0]) - 1 # 最后一列为类标签
base_entropy = calc_entropy(dataset)
best_info_gain = 0.0
best_feature = -1
# 计算每个特征的信息增益 -- ID3算法
for i in range(num_features):
feature_list = [example[i] for example in dataset]
unique_values = set(feature_list)
new_entropy = 0.0
for value in unique_values:
sub_dataset = split_dataset(dataset, i, value)
prob = len(sub_dataset) / float(len(dataset))
new_entropy += prob * calc_entropy(sub_dataset)
info_gain = base_entropy - new_entropy
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = i
return best_feature
def split_dataset(dataset: list, axis: int, value: int):
"""
按照给定特征和值划分数据集
:param dataset: 数据集
:param axis: 特征索引
:param value: 特征值
:return: 划分后的数据集
"""
return_dataset = []
for feature_vec in dataset:
if feature_vec[axis] == value:
reduced_feature_vec = feature_vec[:axis]
reduced_feature_vec.extend(feature_vec[axis + 1:])
return_dataset.append(reduced_feature_vec)
return return_dataset
def calc_entropy(dataset: list):
"""
计算数据集的熵
:param dataset: 数据集
:return: 熵
"""
num_entries = len(dataset)
label_counts = {}
for feature_vec in dataset:
current_label = feature_vec[-1]
if current_label not in label_counts.keys():
label_counts[current_label] = 0
label_counts[current_label] += 1
entropy = 0.0
for key in label_counts:
prob = float(label_counts[key]) / num_entries
entropy -= prob * math.log2(prob)
return entropy
if __name__ == '__main__':
dataset, labels = create_dataset()
feature_labels = []
my_tree = createTree(dataset, labels, feature_labels)
print(my_tree)
输出结果:
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}