目录
一.二叉树的性质
性质概述:
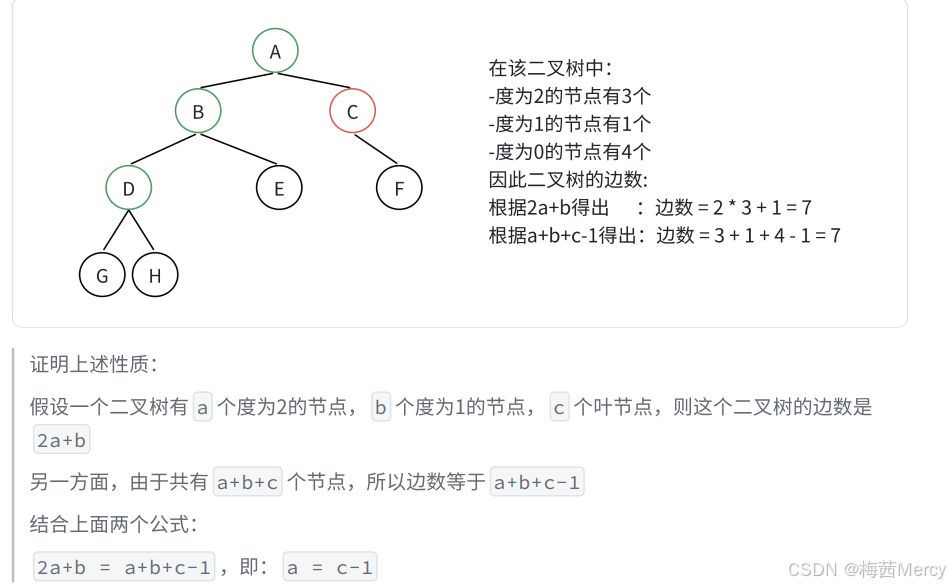
对任何⼀棵⼆叉树,如果叶结点个数为n0 ,度为 2 的分⽀结点个数为n2 ,则n0=n2+1
二.例题详解
1.单值二叉树:
原题出处:https://leetcode.cn/problems/univalued-binary-tree/description/
#include<stdio.h> #include<stdbool.h> struct TreeNode { int val; struct TreeNode* left; struct TreeNode* right; }; bool isUnivalTree(struct TreeNode* root) { if (root == NULL) { return true; } //和左右孩子比较结点的值 if (root->left && root->val != root->left->val)//这里需要注意root->left不能为空 { return false; } if (root->right && root->val != root->right->val) { return false; } return isUnivalTree(root->left) && isUnivalTree(root->right);//注意这里是&& }
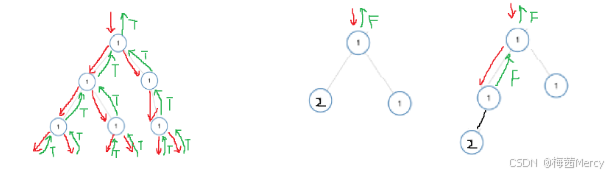
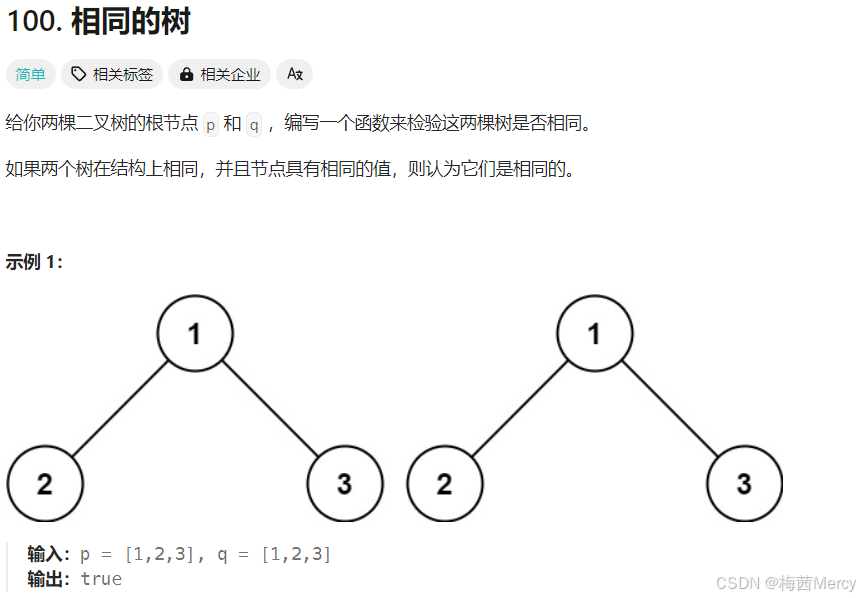
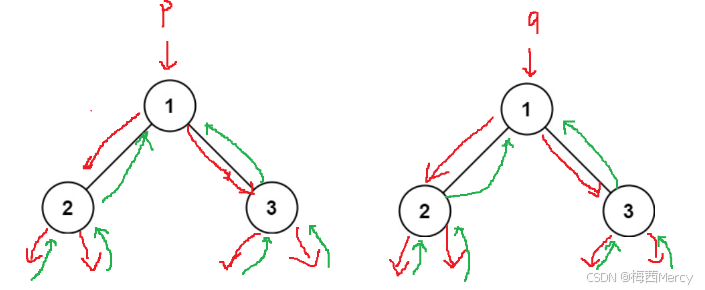
2.相同的树:
原题出处:https://leetcode.cn/problems/same-tree/description/
//相同的树 bool isSameTree(struct TreeNode* p, struct TreeNode* q) { //都为空 if (p == NULL && q == NULL) { return false; } //如果函数走到这里说明并不是都为空,即至少有一个为空 if (p == NULL || q == NULL) { return false; } //如果走到这里说明两个均不为空 if (p->val != q->val) { return false; } //递归验证所有子树 return isSameTree(p->left,q->left) && isSameTree(q->right,p->right); }
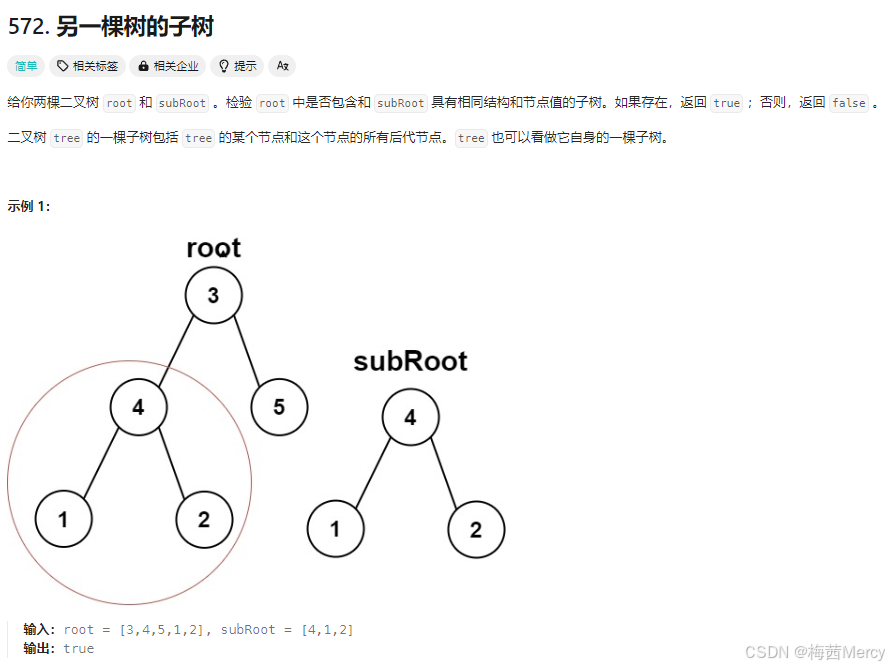
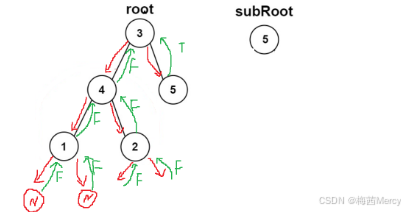
3.另一棵树的子树:
原题出处:https://leetcode.cn/problems/subtree-of-another-tree/description/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) { //都为空 if (p == NULL && q == NULL) { return false; } //如果函数走到这里说明并不是都为空,即至少有一个为空 if (p == NULL || q == NULL) { return false; } //如果走到这里说明两个均不为空 if (p->val != q->val) { return false; } //递归验证所有子树 return isSameTree(p->left,q->left) && isSameTree(q->right,p->right); } //另一棵树的子树 bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) { //当被查找树为空 if (root == NULL) { return false; } //当查找树和被查找相同 if (isSameTree(root, subRoot)) { return true; } //排除上面两种特殊情况就可以用递归判断剩余的一般情况了 return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot); }
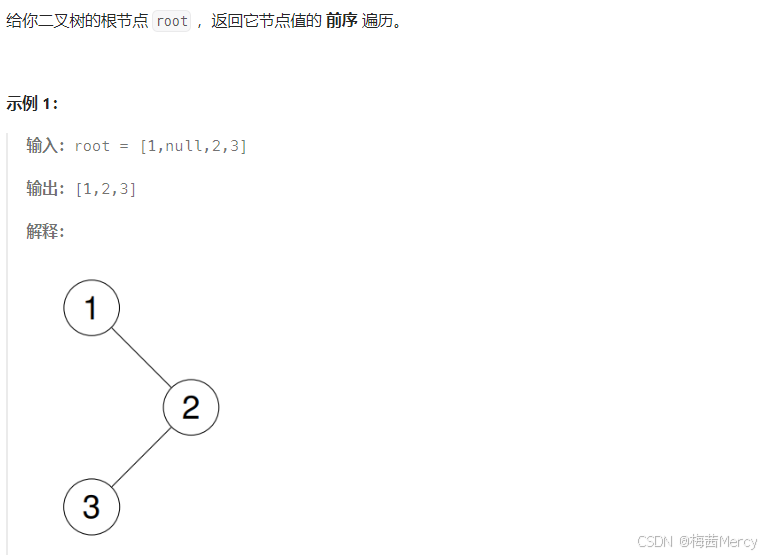
4.二叉树的前序遍历:
原题出处:https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
//returnsize表示需要返回结点的个数数量 typedef struct TreeNode TreeNode; int TreeSize(TreeNode* root) { if (root == NULL) { return 0; } return 1 + TreeSize(root->left) + TreeSize(root->right); } //前序遍历 void preOrder(TreeNode* root,int* arr,int* pi) { if (root == NULL) { return; } arr[(*pi)++] = root->val;//这里另外定义一个pi指针是为了防止在数据存入arr时产生的因为递归而刷新参数而产生的数据覆盖问题 preOrder(root->left); preOrder(root->right); } int* preorderTraversal(struct TreeNode* root, int* returnSize) { //求二叉树结点个数 *returnSize = TreeSize(root); //对返回数组申请*returnSize个int空间 int* arr = (int*)malloc((*returnSize) * sizeof(int)); //前序遍历---将遍历的结果才能出在数组 int i = 0; preOrder(root, arr, &i); return arr; }
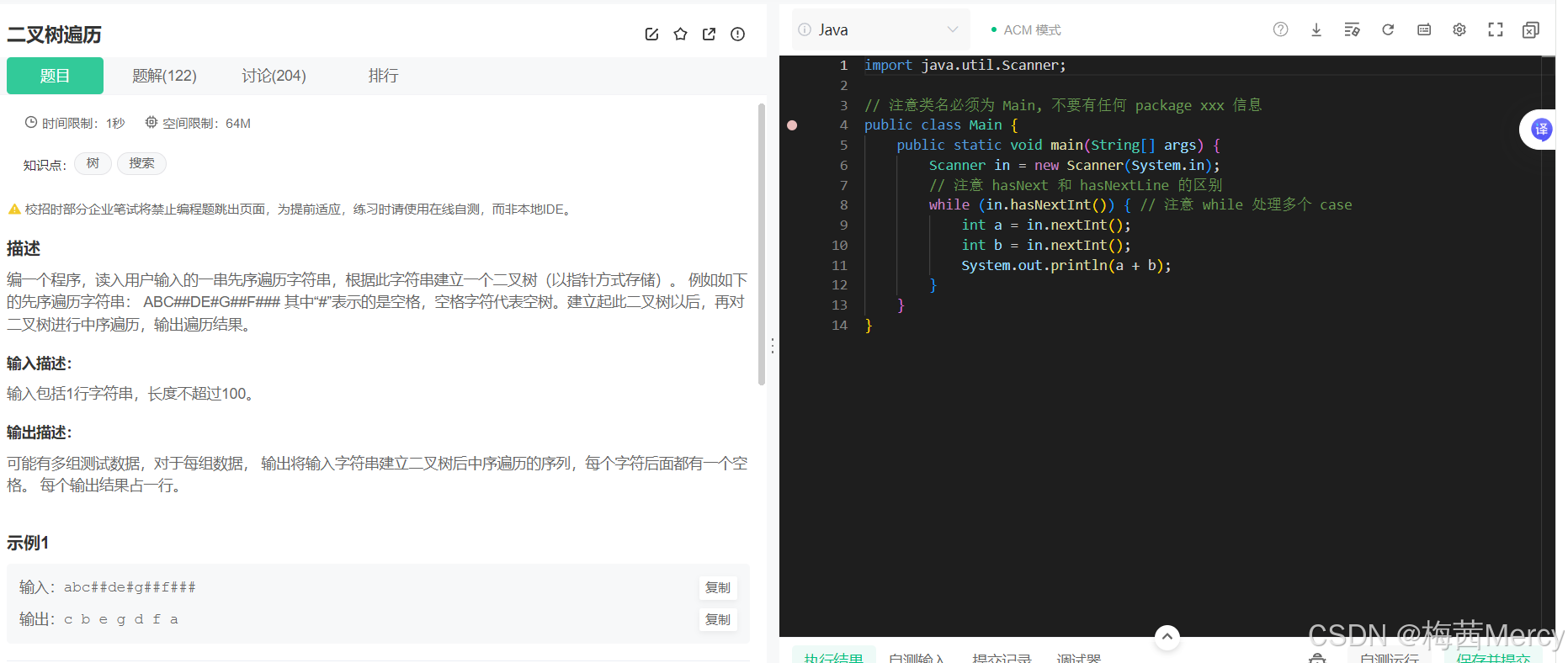
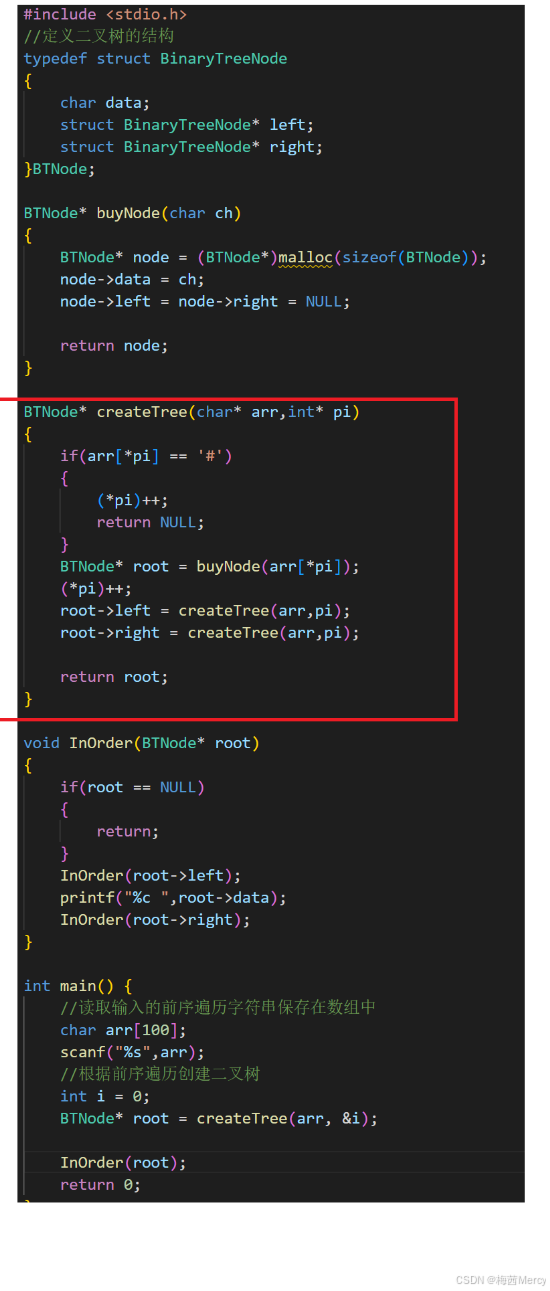
5.二叉树的构建与遍历:
原题出处:https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef
这题主要难点就在于题目要求自己创建树的结构,其他的代码都比较常见,特别需要特别注意的还是在循环建树时将结点类型的元素存入数组时对数组下标所代表的变量取其地址,另外还有一点需要关注的就是代码的逻辑顺序,比如我红框狂出来的地方:首先需要明确的时建树是一个循环递归的过程,因此需要满足递归的基本结构,然后就是在递归基本结构里的排除特殊解的情况中,定义出现“#”就返回,在排除特殊解,进入递归之前,还需注意要先申请供结点结构存入的数组空间,然后再进入层层递归
6.总结:
关于二叉树这一类题型,递归算法是非常常见的,因此通过上述例题我总结出的递归结构也就显而易见:即排除特殊解+函数内的重复递归,但除了这个小技巧之外,我们再看这些题时还需要关注的就是除了递归这个基本结构之外的东西,比如对递归过程中使用计数器时需要取其地址,结点结构也可以作为自定义类型而作为数组元素的灵活使用,此外,在(bfs)广度优先遍历(我在二叉树的链式结构那篇文章里有详细说明)中对于队列结构的运用同样需要理解,因此二叉树的解题代码虽然相较其他类型题目要更加简洁,但其中的逻辑思想却是非常复杂且重要的
欧克,关于二叉树这一类型的题目我就先介绍这么多了,希望可以对你有所帮助
全文终