目录
注:快速幂取模可以用 Python 的内置函数 pow 实现。
解题思路:根据题意可知,(a, b) - (c, d) 中的两个元素位于同一斜线上。(1, 2) - (2, 1) 和 (2, 1) - (1, 2) 算不同的两对,优化一下比较流程计算结果即可。
解题思路:直接kruskal,然后并查集维护连通块大小,从大到小遍历,(并查集维护不小于某边权的最大连通)。
试题A:穿越时空之门
本题总分:5分 本题考察:字符串、枚举

解题思路:进制的转换,数位之和相等的数
cnt = 0
for i in range(1, 2025):
# 二进制
bins = bin(i)[2:].count("1")
# 四进制
four = 0
while i:
four += i % 4
i //= 4
# 累加
cnt += bins == four
print(cnt)试题B:数字串个数
本题总分:5分 本题考察:容斥原理、快速幂取余

解题思路:该数字串只能由数字 1 ~ 9 组成。要减去不包含数字 3 或 7 的。用容斥原理,集合总大小为:9^10000,减去两个8^10000,由于多减了一个两个都不含的,再加上一个 7^10000。
注:快速幂取模可以用 Python 的内置函数 pow 实现。
mod = int(1e9 + 7)
n = 10000
cnt = pow(9, n, mod)
# 去除 no(3) + no(7) 的情况
cnt -= 2 * pow(8, n, mod)
# 补上 no(3 and 7) 的情况
cnt += pow(7, n, mod)
print(cnt % mod)试题C:连连看
本题总分:10分 本题考察:枚举、哈希表

【样例】

【评测用例规模与约定】

解题思路:根据题意可知,(a, b) - (c, d) 中的两个元素位于同一斜线上。(1, 2) - (2, 1) 和 (2, 1) - (1, 2) 算不同的两对,优化一下比较流程计算结果即可。
n, m = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(n)]
# A[a][b] = A[c][d], 处于同一斜线上
cnt = 0
for i in range(n):
for j in range(m):
# 只跟当前行以下的行比较
# 向左下角
for p in range(1, min(n - i, j + 1)):
cnt += A[i][j] == A[i + p][j - p]
# 向右下角
for p in range(1, min(n - i, m - j)):
cnt += A[i][j] == A[i + p][j + p]
print(cnt * 2)试题D:神奇闹钟
本题总分:10分 本题考察:时间处理

【样例】

【评测用例规模与约定】
![]()
解题思路:本题中的输入是标准的 iso 格式日期时间,所以可以直接解析为 datetime 对象。计算上一次响的时间:用总的分钟数减去对时间间隔求余的余数得到上次响的分钟数,再加上起始时间,转化为datetime 对象,最后输出即可。
from datetime import *
bg = datetime.fromisoformat('1970-01-01 00:00:00')
for _ in range(int(input())):
date, time, dif = input().split()
dt = datetime.fromisoformat(date + ' ' + time)
nows = int((dt - bg).total_seconds()) // 60 # 分钟数
nows -= nows % int(dif)
print(bg + timedelta(minutes=nows))试题E:蓝桥村的真相
本题总分:15分 本题考察:分类讨论、找规律

【样例】

【评测用例规模与约定】

解题思路:找规律。1 为谎,0 为真,每 3 个人可能的组合有:010, 001, 100, 111。前三种情况:100 是一个循环 (第三人是前两人的“同或”),如果 n 能被 3 整除,这三种情况就贡献了 n 个说谎的。第四种情况:全都是 111,贡献了 n 个说谎的。
for _ in range(int(input())):
n = int(input())
print(n * (1 + (n % 3 == 0)))
试题F:魔法巡游
本题总分:15分 本题考察:哈希表、DP

【样例】

【评测用例规模与约定】
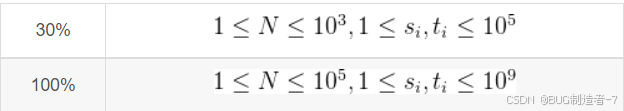
解题思路:用两个哈希表 f1、f2 分别统计 s、t 序列中上一个包含 0、2、4 的符石作为序列末尾的最长序列长度。注意要使用更新前的 f1 来更新 f2 和用更新前的 f2 更新 f1,所以需要对其中一个哈希表拷贝一下。最后输出两个哈希表中的最大值即可。
cin = lambda: list(map(int, input().split()))
input()
f1, f2 = [-1] * 5, [-1] * 5
digs = (0, 2, 4)
def update(s, f1, f2):
for d in digs:
if str(d) in s:
f1[d] = max(f1[d], max(f2[i] + 1 for i in digs if str(i) in s))
for s, t in zip(cin(), cin()):
s, t = str(s), str(t)
f2_ = f2.copy() # 拷贝
update(t, f2, f1)
for d in digs:
if str(d) in s and f1[d] < 0:
f1[d] = max(*f1, 1) # 确保先从 s 开始走
update(s, f1, f2_)
print(max(f1 + f2))试题G:缴纳过路费
本题总分:20分 本题考察:缩点、并查集、DFS


【样例】

【评测用例规模与约定】

解题思路:直接kruskal,然后并查集维护连通块大小,从大到小遍历,(并查集维护不小于某边权的最大连通)。
from sys import *
setrecursionlimit(10**6)
cin = lambda: list(map(int, input().split()))
n, m, l, r = cin()
e = [set() for _ in range(n + 1)]
# s[i] == i 表示 i 为新点,sz[i] 表示新点 i 的大小
s, sz = list(range(n + 1)), [1] * (n + 1)
def find(x):
if s[x] == x:
return x
s[x] = find(s[x])
return s[x]
edges = [cin() for _ in range(m)]
for u, v, w in edges:
if w > r: continue # 舍弃
su, sv = find(u), find(v)
if w < l and su - sv: # 边权小于 l 且不在同一集合
# 合并
s[su] = sv
sz[sv] += sz[su]
# 以新点建图
for u, v, w in edges:
if l <= w <= r:
su, sv = find(u), find(v)
e[su].add(sv)
e[sv].add(su)
vis = [False] * (n + 1)
def dfs(u, block): # 寻找连通块,返回值表示该块内点的集合的总大小
block.append(u)
res, vis[u] = sz[u], True
for v in e[u]:
if vis[v]: continue
res += dfs(v, block)
return res
ans = 0
for i in range(1, n + 1):
if s[i] == i and not vis[i]:
block = []
t = dfs(i, block)
for u in block:
ans += sz[u] * (t - sz[u])
print(ans // 2)试题H:纯职业小组
本题总分:20分 本题考察:贪心、思维


【样例】

【评测用例规模与约定】

解题思路:找到一个数,能其恰好能组成 k 组,并且这个数尽可能大。只有当每一组都选完还组不成 k 组的时候输出 -1,否则一定能组成 k 组。如果能组成 k 组,那么设一个计数器 m = k 表示hai缺几组没有凑够。
from collections import *
cin = lambda: list(map(int, input().split()))
for _ in range(int(input())):
n, k = cin()
cnt = Counter()
for i in range(n):
a, b = cin()
cnt[a] += b
if sum(c // 3 for c in cnt.values()) < k:
print(-1)
continue
ans, v = 0, list(cnt.values())
for i in range(len(v)):
if v[i] < 3:
ans += v[i]
v[i] = 0
continue
t = min((v[i] - 2) // 3, k)
v[i] -= t * 3 + 2
ans += t * 3 + 2
k -= t
if not k:
print(ans - 2)
continue
v.sort()
print(ans + sum(v[-k:]) - (v[-k] == 2))