探秘Transformer系列之（28）--- DeepSeek MLA（下）

发布于：2025-04-21 ⋅ 阅读:(44) ⋅ 点赞:(0)

探秘Transformer系列之（28）— DeepSeek MLA（下）

文章目录

0x00 概述

书接上文，我们在本篇看看代码。

注：

  • 全部文章列表在这里，估计最终在35篇左右，后续每发一篇文章，会修改此文章列表。 探秘Transformer系列之文章列表
  • 本系列是对论文、博客和代码的学习和解读，借鉴了很多网上朋友的文章，在此表示感谢，并且会在参考中列出。因为本系列参考文章太多，可能有漏给出处的现象。如果原作者或者其他朋友发现，还请指出，我在参考文献中进行增补。

探秘Transformer系列之（1）：注意力机制

探秘Transformer系列之（2）—总体架构

探秘Transformer系列之（3）—数据处理

探秘Transformer系列之（4）— 编码器 & 解码器

探秘Transformer系列之（5）— 训练&推理

探秘Transformer系列之（6）— token

探秘Transformer系列之（7）— embedding

探秘Transformer系列之（8）— 位置编码

探秘Transformer系列之（9）— 位置编码分类

探秘Transformer系列之（10）— 自注意力

探秘Transformer系列之（11）— 掩码

探秘Transformer系列之（12）— 多头自注意力

探秘Transformer系列之（13）— FFN

探秘Transformer系列之（14）— 残差网络和归一化

探秘Transformer系列之（15）— 采样和输出

探秘Transformer系列之（16）— 资源占用)

探秘Transformer系列之（17）— RoPE（上）

探秘Transformer系列之（17）— RoPE（下）

探秘Transformer系列之（18）— FlashAttention

探秘Transformer系列之（19）----FlashAttention V2 及升级版本

探秘Transformer系列之（20）— KV Cache

探秘Transformer系列之（21）— MoE

探秘Transformer系列之（22）— LoRA

探秘Transformer系列之（23）— 长度外推

探秘Transformer系列之（24）— KV Cache优化

探秘Transformer系列之（25）— KV Cache优化之处理长文本序列

探秘Transformer系列之（26）— KV Cache优化 之 PD分离or合并

探秘Transformer系列之（27）— MQA & GQA

0x04 代码

我们主要使用V2的代码来分析，因为条理更加清晰。也需要注意的是，DeepSeek的代码在很多地方和论文不一致。V2中的DeepseekV2Attention的实现本质上和V3中的native一样，其实并没有节省KV-Cache，V3版本的非native版本是跟论文一致，节省了显存。

4.1 配置

我们摘录一些相关配置信息如下。在 Naive 实现中，512 维的 Latent KV c K V c^{KV} cKV 被映射回对应 128 个 head，每个 head 128 维的 k C k^C kC 和 v C v^C vC，然后再拼接上位置向量 k R k^R kR ，最终形成标准的 q、k、v 输入到标准的 Multi Head Attention 进行 Attetion 计算。另外，代码中也使用了norm，在论文中也有相应提及。

具体配置信息如下。其中：

  • 键和值的压缩维度 d c d_c dc​ ：设置为 512 ，原始嵌入维度 𝑑=5120，比例为 1/10。由于键和值在推理时需要缓存，因此采用较大的压缩比例以显著减少内存开销。
  • 查询的压缩维度 d c ′ d'_c dc′​ ：设置为 1536 ，比例为 0.3 。查询在训练时需要频繁计算，因此采用较小的压缩比例以保留更多信息，确保模型性能。
"num_hidden_layers": 60, # Transformer层的数量
"hidden_size": 5120, # 隐藏层的大小
"num_attention_heads": 128, # 注意力头的数量
"kv_lora_rank": 512, # KV压缩维度
"q_lora_rank": 1536, # Query压缩维度
"qk_rope_head_dim": 64, # 解耦Query和Key的每个头部维度
"n_shared_experts": 2, # MoE层中的共享专家数量
"n_routed_experts": 160, # MoE层中的路由专家数量
"moe_intermediate_size": 1536, # 每个MoE专家的中间隐藏层的维度
"num_experts_per_tok": 6, # 每个token激活的专家数量
"routed_scaling_factor": 16.0, # 路由专家的缩放因子
"rms_norm_eps": 1e-06 # RMS归一化的epsilon值

4.2 定义

给定输入向量 h t ∈ R B × L × 5120 h_t \in \mathbb{R}^{B \times L \times 5120} ht​∈RB×L×5120，其中 B B B为batch size， L L L为sequence length。

class DeepseekV2Attention(nn.Module):
    """Multi-headed attention from 'Attention Is All You Need' paper"""
    def __init__(self, config: DeepseekV2Config, layer_idx: Optional[int] = None):
        super().__init__()
        self.config = config
        self.layer_idx = layer_idx
        self.attention_dropout = config.attention_dropout
        self.hidden_size = config.hidden_size
        self.num_heads = config.num_attention_heads
        self.max_position_embeddings = config.max_position_embeddings
        self.rope_theta = config.rope_theta
        # 对应 query 压缩后的隐向量的维度 d'_c
        self.q_lora_rank = config.q_lora_rank
        # query和key的隐藏向量中，应用rope部分的维度，对应d_h^R
        self.qk_rope_head_dim = config.qk_rope_head_dim
        # 对应 key-value 压缩后的隐向量维度 d_c
        self.kv_lora_rank = config.kv_lora_rank
        # value 的一个注意力头的隐藏层维度
        self.v_head_dim = config.v_head_dim
        # 向量中不应用rope部分的维度
        self.qk_nope_head_dim = config.qk_nope_head_dim
        # 每一个注意力头的维度应该是nope和rope两部分之和
        self.q_head_dim = config.qk_nope_head_dim + config.qk_rope_head_dim
        self.is_causal = True

        # MLA 中对 Q 投影矩阵也做了一个低秩分解，对应生成 q_a_proj 和 q_b_proj 两个矩阵，即两阶段投影：先将hidden_size投影到q_lora_rank，再投影到最终维度
        # 对query进行压缩，即down-projection。即，第一阶段投影：hidden_size -> q_lora_rank，对应论文公式中的W^DQ
        self.q_a_proj = nn.Linear(
            self.hidden_size, config.q_lora_rank, bias=config.attention_bias
        )
        self.q_a_layernorm = DeepseekV2RMSNorm(config.q_lora_rank)
        # 对压缩后的query映射成高维，即up-projection。对应上述公式中的W^UQ和W^QR合并后的大矩阵，仅仅只是内存放在一起。
        # q_head_dim = config.qk_nope_head_dim + config.qk_rope_head_dim = 128 + 64
        self.q_b_proj = nn.Linear(
            config.q_lora_rank, self.num_heads * self.q_head_dim, bias=False
        )

        # KV向量的生成也是先投影到一个低维的 compressed_kv 向量（对应c_t^{KV}），再升维展开
        # 对应论文公式中的W^{DKV}和W^{KR}
        self.kv_a_proj_with_mqa = nn.Linear(
            self.hidden_size,
            config.kv_lora_rank + config.qk_rope_head_dim,
            bias=config.attention_bias,
        )
        self.kv_a_layernorm = DeepseekV2RMSNorm(config.kv_lora_rank)
        # 对应论文公式中的W^{UK}和W^{UV}，由于 W^{UK} 只涉及 non-rope 的部分，所以维度中把 qk_rope_head_dim 去掉了
        self.kv_b_proj = nn.Linear(
            config.kv_lora_rank,
            self.num_heads
            * (self.q_head_dim - self.qk_rope_head_dim + self.v_head_dim),
            bias=False,
        )

        # 对应论文公式的第 47 行
        self.o_proj = nn.Linear(
            self.num_heads * self.v_head_dim,
            self.hidden_size,
            bias=config.attention_bias,
        )
        self._init_rope()

        self.softmax_scale = self.q_head_dim ** (-0.5)
        if self.config.rope_scaling is not None:
            mscale_all_dim = self.config.rope_scaling.get("mscale_all_dim", 0)
            scaling_factor = self.config.rope_scaling["factor"]
            if mscale_all_dim:
                mscale = yarn_get_mscale(scaling_factor, mscale_all_dim)
                self.softmax_scale = self.softmax_scale * mscale * mscale

对应的一些信息如下。把整个计算流程拆成 q_nope, k_nope, k_pe, k_nope 这四个部分就是为了把RoPE进行解耦。两个pe结尾的变量就是用于储存旋转位置编码的信息。Deepseek-V2将kv cache压缩到了同一个小矩阵中，后面再解压缩出来。

# q = q.view(bsz, q_len, num_heads, q_head_dim).transpose(1, 2)
# q_nope, q_pe = torch.split(q, [qk_nope_head_dim, qk_rope_head_dim], dim=-1)
q_pe : torch.Size([16, 128, 1, 64])
q_nope : torch.Size([16, 128, 1, 128])
# query_states = k_pe.new_empty(bsz, num_heads, q_len, q_head_dim)
query_states : torch.Size([16, 128, 1, 192])
    
# kv = .view(bsz, kv_seq_len, num_heads, qk_nope_head_dim + v_head_dim).transpose(1, 2)
# k_nope, value_states = torch.split(kv, [qk_nope_head_dim, v_head_dim], dim=-1)
value_states : torch.Size([16, 128, 1024, 128])
k_nope : torch.Size([16, 128, 1024, 128])  
# k_pe = k_pe.view(bsz, kv_seq_len, 1, qk_rope_head_dim).transpose(1, 2)
k_pe : torch.Size([16, 1, 1024, 64])
# key_states = k_pe.new_empty(bsz, num_heads, kv_seq_len, q_head_dim)
key_states : torch.Size([16, 128, 1024, 192])

self = {DeepseekAttention}  
 hidden_size = {int} 5120
 kv_a_layernorm = {DeepseekV2RMSNorm} DeepseekV2RMSNorm()
 kv_a_proj_with_mqa = {Linear} Linear(in_features=5120, out_features=576, bias=False)
 kv_b_proj = {Linear} Linear(in_features=512, out_features=32768, bias=False)
 kv_lora_rank = {int} 512
 num_heads = {int} 128
 o_proj = {Linear} Linear(in_features=16384, out_features=5120, bias=False)
 q_a_layernorm = {DeepseekV2RMSNorm} DeepseekV2RMSNorm()
 q_a_proj = {Linear} Linear(in_features=5120, out_features=1536, bias=False)
 q_b_proj = {Linear} Linear(in_features=1536, out_features=24576, bias=False)
 q_head_dim = {int} 192
 q_lora_rank = {int} 1536
 qk_nope_head_dim = {int} 128
 qk_rope_head_dim = {int} 64
 rotary_emb = {DeepseekV2RotaryEmbedding} DeepseekV2RotaryEmbedding()
 softmax_scale = {Tensor} tensor(0.0723, dtype=torch.bfloat16)
 v_head_dim = {int} 128

另外，https://github.com/sgl-project/sglang/discussions/3082 这里阐释了为何使用norm。

4.3 操作Q

我们把Q相关的代码都合并在一起进行分析。总的流程是：模型处理上一层计算出的隐藏状态（hidden_size=5120）时，首先会将模型的q压缩到 q_lora_rank 这一维度（设定为1536），再扩展到 q_b_proj 的输出维度（num_heads * q_head_dim），最后切分成 q_pe 和 q_nope 两个部分。

4.3.1 变量定义

MLA 中对 Q 投影矩阵 W Q W^Q WQ做了一个低秩分解，对应生成 q_a_proj 和 q_b_proj 两个矩阵。

  • q_a_proj 大小为 [hidden_size, q_lora_rank] = [5120, 1536]，对应公式中的 W D Q W^{DQ} WDQ，用来降维。
  • q_b_proj 大小为 [q_lora_rank, num_heads * q_head_dim] = [q_lora_rank, num_attention_heads * (qk_nope_head_dim + qk_rope_head_dim)] = [1536, 128*(128+64)] = [1536, 24576] ，用来升维，对应公式中的 W U Q W^{UQ} WUQ 和 W Q R W^{QR} WQR合并后的大矩阵。因为从公式来看这两个矩阵都需要和 c t Q c_t^Q ctQ​计算，所以可以合并矩阵后再进行拆分。对于一个head，用一个128维度的向量表示其文本信息，以及一个64维度的向量来表示其旋转位置编码信息。前面的128维度，称为nope，后面的64维度，称为rope。
self.num_heads = config.num_attention_heads # 128
self.q_lora_rank = config.q_lora_rank # 1536
self.q_head_dim = config.qk_nope_head_dim + config.qk_rope_head_dim # 128 + 64

# 对query进行压缩，即down-projection
self.q_a_proj = nn.Linear(
    self.hidden_size, config.q_lora_rank, bias=config.attention_bias
)
self.q_a_layernorm = DeepseekV2RMSNorm(config.q_lora_rank)
# 对压缩后的query映射成高维，即up-projection
self.q_b_proj = nn.Linear(
    config.q_lora_rank, self.num_heads * self.q_head_dim, bias=False
)
4.3.2 变量操作

在DeepSeek-V2中，Q向量也采用了低秩压缩的方式。

  • 首先，将输入向量投影到一个1536维的低维空间： c t Q = W D Q , h t ∈ R B × L × 1536 c_t^Q = W^{DQ} ,h_t \in \mathbb{R}^{B \times L \times 1536} ctQ​=WDQ,ht​∈RB×L×1536。对应论文第37号公式。
  • 然后，将其投影到 R H × 128 \mathbb{R}^{H \times 128} RH×128的多头向量空间上（其中 H = 128 H=128 H=128是heads数），得到了Q向量的第一部分：$ q_t^C = W^{UQ} c_t^Q \in \mathbb{R}^{B \times L \times H \times 128}$。对应第38号公式。
  • 再将其投影到 R H × 64 \mathbb{R}^{H \times 64} RH×64上并使用RoPE嵌入位置信息，得到Q向量的第二部分： q t R = R o P E ( W K R h t ) ∈ R B × L × H × 64 q_t^R = \mathrm{RoPE}(W^{KR} h_t) \in \mathbb{R}^{B \times L \times H \times 64} qtR​=RoPE(WKRht​)∈RB×L×H×64。对应第39号公式。每个head有自己的旋转位置编码，每个head之间不共享。
  • 将两部分拼接的到最终的Q向量： q t = [ q t C , q t R ] ∈ R B × L × H × 192 q_t = [q_t^C, q_t^R] \in \mathbb{R}^{B \times L \times H \times 192} qt​=[qtC​,qtR​]∈RB×L×H×192。对应第40号公式。

在具体的实现过程中其输入为 hidden_states 向量，对应公式中的 h t ℎ_t ht​。是一个大小为 [batch_Size, sequence_length, hidden_size] 的矩阵，其中 hidden_size 具体为 5120。后续的nope指代非rope。

# hidden_states对应公式中的h_t，hidden_states的shape是(batch_size, seq_length, hidden_size)，其中 hidden_size为 5120，是num_head * q_head_dim
bsz, q_len, _ = hidden_states.size()

# 下面两行代码对应第37、38号公式，先降维再升维。q_b_proj维度是[1536, 24576]，q_a_proj维度是[5120, 1536]，是W^Q [5120, 24576]矩阵的低秩分解。即[5120, 24576] -> [5120, 1536] * [1536, 24576] 
# 首先，使用全连接层（self.q_a_proj）对输入的隐状态（hidden_states）进行降维投影
# 然后，使用全连接层（self.q_b_proj）对压缩的向量进行上投影  
q = self.q_b_proj(self.q_a_layernorm(self.q_a_proj(hidden_states)))

# 重塑为多头形式，是第40号公式的前置准备操作，或者说是40号公式的反向操作
# q_pe 要扔给 RoPE模块，所以需要重整下形状
q = q.view(bsz, q_len, self.num_heads, self.q_head_dim).transpose(1, 2)

# 把最后一维切分成nope和rope两部分
# 将最后一层 192 的hidden_states切分为 128 (qk_nope_head_dim) + 64 (qk_rope_head_dim)，即将查询表示（q）分为两部分：没有经过位置编码的部分（q_nope）和经过位置编码的部分（q_pe），q_nope表示不需要应用RoPE的，q_pe表示需要应用RoPE的
q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)

# 第39号公式，给q和k施加RoPE
q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)

# 初始化查询状态（query_states）的张量，这个张量将用于存储融合了解耦RoPE的查询表示，其中q_head_dim = qk_nope_head_dim + qk_rope_head_dim = 128 + 64 = 192
query_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)

# 下面两行对应第40号公式
# 将未经过位置编码的查询表示（q_nope）复制到 query_states 张量的前一部分，即那些不包含位置编码的维度。
# 这样做可以有利于后续将原始的查询表示与含有位置编码信息的查询表示分开来处理
query_states[:, :, :, : self.qk_nope_head_dim] = q_nope # 128
query_states[:, :, :, self.qk_nope_head_dim :] = q_pe # 64

4.4 操作KV

我们把KV相关的代码都合并在一起进行分析。对于kv矩阵的设计，模型使用了kv压缩矩阵设计（只有576维），在训练时进行先降维再升维。在模型推理的时候，需要缓存的量变成 compressed_kv，经过 kv_b_proj 升高维度得到 k,v 的计算结果。

4.4.1 变量定义

KV向量和Q向量类似，也做了一个低秩分解，对应生成 kv_a_proj_with_mqa和 kv_b_proj 两个矩阵。

  • kv_a_proj_with_mqa 大小为 [hidden_size， kv_lora_rank + qk_rope_head_dim] = [5120, 512 + 64] = [5120, 576]，对应上述公式中的 W D K V W^{DKV} WDKV 和 W K R W^{KR} WKR的合并矩阵，用来把输入先投影到一个低维的空间（对应 C t K V C_t^{KV} CtKV​），同时做两种降维操作（nope，rope的前置操作）。因为因为从公式来看这两个矩阵都需要和 h t h_t ht​计算，所以可以合并矩阵计算后再进行拆分。输出的维度则是512+64=576了。前面的512维度是给kv的，后面的64维度是给key的旋转位置编码的。
  • kv_b_proj 大小为 [kv_lora_rank，num_heads * (q_head_dim - qk_rope_head_dim + v_head_dim)] = [512, 128*((128+64)-64+128)] = [512, 32768]，对应上述公式中的 W U K W^{UK} WUK 和 W U V W^{UV} WUV的合并矩阵。由于 W U K W^{UK} WUK 只涉及nope 的部分，所以维度中把 qk_rope_head_dim 去掉了。192-64是把key表示向量中的64维度的旋转位置编码向量从192维度中减去；然后的128维度是留给value的，因为value不需要考虑位置信息。需要考虑位置信息的只有query和key。

或者说，通过kv_a_proj_with_mqa 来对head脱敏，即得到的张量和具体的head无关；通过kv_b_proj来重新恢复成对每个head敏感，得到的是形如[1, 16, 26, 128]这样的，和具体16个head分别相关的张量。

self.kv_lora_rank = kv_lora_rank # 512，key和value各占256维度
self.qk_rope_head_dim = config.qk_rope_head_dim # 64
self.q_head_dim = config.qk_nope_head_dim + config.qk_rope_head_dim # 128 + 64
self.v_head_dim = config.v_head_dim # 128
self.hidden_size = config.hidden_size # 5120

# 计算压缩后的latent kv以及需要缓存的应用RoPE的k的部分：k_t^R(前置条件)，即把隐向量的5120维度 映射到 config.kv_lora_rank + config.qk_rope_head_dim = 512 + 64维度
self.kv_a_proj_with_mqa = nn.Linear(
    self.hidden_size,
    config.kv_lora_rank + config.qk_rope_head_dim,
    bias=config.attention_bias,
)
self.kv_a_layernorm = DeepseekV2RMSNorm(config.kv_lora_rank)
# 计算up-projection后的不应用RoPE的k的部分 和 up-projection后的v的结果
self.kv_b_proj = nn.Linear(
    config.kv_lora_rank,
    self.num_heads
    * (self.q_head_dim - self.qk_rope_head_dim + self.v_head_dim),
    bias=False,
)
4.4.2 变量操作

计算KV向量时，有几个和公式中不同的地方，即把某些矩阵操作打包在一起执行（同时将K，V的向量一起产出了)，后续再拆分开。

  • 首先需要将输入向量投影为512维的联合压缩表示： c t K V = W D K V h t ∈ R B × L × 512 c_t^{KV} = W^{DKV} h_t \in \mathbb{R}^{B \times L \times 512} ctKV​=WDKVht​∈RB×L×512，对应第41号公式。

  • 与Q向量的计算过程类似，K向量的第一部分是将 c t K V c_t^{KV} ctKV​通过投影解压缩到 R H × 128 \mathbb{R}^{H \times 128} RH×128的多头向量空间： k t C = W U K c t K V ∈ R B × L × H × 128 k_t^C = W^{UK} c_t^{KV} \in \mathbb{R}^{B \times L \times H \times 128} ktC​=WUKctKV​∈RB×L×H×128，对应第42号公式。注意：此处增加了一个头维度。

  • K的第二部分是将输入向量投影到64维向量空间并施加RoPE嵌入位置信息： k t R = R o P E ( W K R h t ) ∈ R B × L × 64 k_t^R = \mathrm{RoPE}(W^{KR} h_t) \in \mathbb{R}^{B \times L \times 64} ktR​=RoPE(WKRht​)∈RB×L×64，对应第43号公式。

  • 与Q不同的是，完整的K是将K的第二部分广播到每个head后与第一部分拼接得到：
    k t = [ k t , 1 C k t R k t , 2 C k t R ⋮ ⋮ ] ∈ R B × L × H × 192 k_t = \begin{bmatrix} k_{t,1}^C & k_t^R \\ k_{t,2}^C & k_t^R \\ \vdots & \vdots \\ \end{bmatrix} \in \mathbb{R}^{B \times L \times H \times 192} kt​= ​kt,1C​kt,2C​⋮​ktR​ktR​⋮​ ​∈RB×L×H×192
    也就是说，每个head的RoPE部分是完全相同的。此处对应第44号公式。再强调下：对于query，每个head有自己的旋转位置编码向量；key则是所有heads共享同一个旋转位置编码向量。

  • V向量的计算较为简单，直接将 c t K V c_t^{KV} ctKV​解压缩到 R H × 128 \mathbb{R}^{H \times 128} RH×128即可： v t = W U V c t K V ∈ R B × L × H × 128 v_t = W^{UV} c_t^{KV} \in \mathbb{R}^{B \times L \times H \times 128} vt​=WUVctKV​∈RB×L×H×128，对应第45号公式。

通过维度分析可以看到 kv_lora_rank 是 qk_nope_head_dim 的 4 倍且 K 和 V 共享 latent state，qk_rope_head_dim 只有 qk_nope_head_dim 的一半，结合起来 4+1/2=9/2，是 正式下图中 MLA KVCache per Token 大小的来源。

具体的代码实现如下，可以发现除了在对q做计算时涉及到gemv之外，也就是q = self.q_b_proj(self.q_a_layernorm(self.q_a_proj(hidden_states)))，其它地方的矩阵乘运算q_len维度都是和num_heads在一起做计算，而num_heads在Deepseek2的配置里面已经是128了，导致其它的Matmul几乎都落在了计算密集的范畴。

# 使用MQA（Multi-Query Attention）对输入的隐状态进行处理，得到压缩后的键值对表示（compressed_kv），对应41号公式和43号（还没有加 rope）。此时compressed_kv就是公式中的c_t^{KV}+W^{KR}h_t，形状是[B, q_len, kv_lora_rank + qk_rope_head_dim]，kv_lora_rank是d_t
compressed_kv = self.kv_a_proj_with_mqa(hidden_states)

# 将压缩后的键值对表示分为两部分：低秩压缩的键值对部分和经过位置编码的键部分（k_pe），分别对于nope和rope。这是第44号公式的前置准备操作，或者说是44号公式的反向操作
# 此时compressed_kv才是公式中的c_t^{KV}，k_pe是公式中的W^{KR}h_t
compressed_kv, k_pe = torch.split(
    compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1
)

# k_pe 要传给 RoPE模块，所以需要重整下形状，增加注意力头这个维度
k_pe = k_pe.view(bsz, q_len, 1, self.qk_rope_head_dim).transpose(1, 2)

# 计算得到k^C和v^C
# 1. 对压缩后的键值对升维，包括RMSNorm（self.kv_a_layernorm）和全连接层（self.kv_b_proj，对应W^{UK}和W^{UV}），是42号和45号公式结合体的前半部分，得到W^{UK}c^{KV}_t（k^C_t）和W^{UV}c^{KV}_t（V^C_t），但此时k^C_t和V^C_t是拼接在一起的
# 2. 用view()和transpose()函数将MLA展开成标准MHA的形式。注意：此处增加了一个头维度
kv = (
    self.kv_b_proj(self.kv_a_layernorm(compressed_kv))
    .view(bsz, q_len, self.num_heads, self.qk_nope_head_dim + self.v_head_dim)
    .transpose(1, 2)
)

# 使用torch.split函数将k^C_t和V^C_t分离开，是42号和45号公式结合体的后半部分。因为 kv_b_proj 包括 W^{UK} 和 W^{UV}，因此要把它们的计算结果分离出来，分别在不同的地方吸收，最终拆分成两部分：
# k_nope是没有经过位置编码的键部分，不包含位置信息。维度为[B, num_head, kv_seq_len, qk_nope_head_dim]
# value_states是值部分，用于后续的位置编码和注意力权重计算，维度为[B, num_head, kv_seq_len, v_head_dim]
k_nope, value_states = torch.split(
    kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1
)

# 获取key/value的序列长度，即包含当前位置可用上下文的长度
kv_seq_len = value_states.shape[-2]
if past_key_value is not None:
    kv_seq_len += past_key_value.get_usable_length(kv_seq_len, self.layer_idx)

# 调用self.rotary_emb函数，根据value_states和更新后的序列长度kv_seq_len计算RoPE的cos和sin值
cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)

# 使用apply_rotary_pos_emb函数对W^{KR}h_t施加RoPE，得到k_t^R，即k_pe变量
q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)

# 初始化键状态（key_states）的张量，存储融合了解耦RoPE的键表示
key_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
key_states[:, :, :, : self.qk_nope_head_dim] = k_nope # k^C_t
key_states[:, :, :, self.qk_nope_head_dim :] = k_pe # k^C_t + k_t^R

4.5 注意力操作

4.5.1 变量定义

o_proj对应矩阵 W O W^O WO，大小为[num_heads * v_head_dim, hidden_states]=[128 * 128, 5120]。

self.v_head_dim = config.v_head_dim # 128
self.num_heads = config.num_attention_heads # 128
self.hidden_size = config.hidden_size # 5120

self.o_proj = nn.Linear( # 对应第47号公式
    self.num_heads * self.v_head_dim,
    self.hidden_size,
    bias=config.attention_bias,
)
4.5.2 变量操作

生成 QKV 向量之后的流程就基本上等同于标准的 MHA 计算了。唯一的区别在于只有 q_pe, k_pe 这两个部分给加上了 rope。具体流程如下：

首先计算attention score：
a = s o f t m a x ( q t ⊤ k t + M a s k 192 ) = s o f t m a x ( q t C ⊤ k t C + q t R ⊤ k t R + M a s k 128 + 64 ) ∈ R B × L × H × L a = \mathrm{softmax}\left(\frac{q_t^\top k_t + \mathrm{Mask}}{\sqrt{192}}\right) = \mathrm{softmax}\left(\frac{{q_t^C}^\top k_t^C + {q_t^R}^\top k_t^R + \mathrm{Mask}}{\sqrt{128 + 64}} \right) \in \mathbb{R}^{B \times L \times H \times L} a=softmax(192 ​qt⊤​kt​+Mask​)=softmax(128+64 ​qtC​⊤ktC​+qtR​⊤ktR​+Mask​)∈RB×L×H×L
然后计算对V的加权和，并将所有head压平，得到Attention输出：
o = a ⋅ v t ∈ R B × L × H × 128 ≅ R B × L × 16384 o = a \cdot v_t \in \mathbb{R}^{B \times L \times H \times 128} \cong \mathbb{R}^{B \times L \times 16384} o=a⋅vt​∈RB×L×H×128≅RB×L×16384
最后经过另一个矩阵的投影，就能得到MLA的最终输出：
u = W O o ∈ R B × L × 5120 u = W^O o \in \mathbb{R}^{B \times L \times 5120} u=WOo∈RB×L×5120

# 更新和拼接历史 KVCache，将当前位置之前的压缩后的kv以及应用过rope的k的部分拼接进去，可以看到这里存储的是展开后的 MHA KVCache
if past_key_value is not None:           
    cache_kwargs = {"sin": sin, "cos": cos}  # Specific to RoPE models
    key_states, value_states = past_key_value.update( # 更新kv cache
        key_states, value_states, self.layer_idx, cache_kwargs
    )

# 后续就是标准的 MHA 代码，代码 Q^T*K*V*O
attn_weights = (
    torch.matmul(query_states, key_states.transpose(2, 3)) * self.softmax_scale
)

if attention_mask is not None:
    attn_weights = attn_weights + attention_mask

# upcast attention to fp32
attn_weights = nn.functional.softmax(
    attn_weights, dim=-1, dtype=torch.float32
).to(query_states.dtype)
attn_weights = nn.functional.dropout(
    attn_weights, p=self.attention_dropout, training=self.training
)
attn_output = torch.matmul(attn_weights, value_states)
attn_output = attn_output.transpose(1, 2).contiguous()
attn_output = attn_output.reshape(bsz, q_len, self.num_heads * self.v_head_dim)
attn_output = self.o_proj(attn_output)
if not output_attentions:
    attn_weights = None

return attn_output, attn_weights, past_key_value

4.6 前向传播

我们把完整的前向传播代码摘录如下，大家可以更好的理解。

def forward(
    self,
    hidden_states: torch.Tensor,
    attention_mask: Optional[torch.Tensor] = None,
    position_ids: Optional[torch.LongTensor] = None,
    past_key_value: Optional[Cache] = None, # V2代码中，kv cache存储的是全部缓存，不是压缩后的
    output_attentions: bool = False,
    use_cache: bool = False,
    **kwargs,
) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]:
    # hidden_states对应公式中的h_t，的shape是(batch_size, seq_length,hidden_size)
    bsz, q_len, _ = hidden_states.size()

    q = self.q_b_proj(self.q_a_layernorm(self.q_a_proj(hidden_states)))
    q = q.view(bsz, q_len, self.num_heads, self.q_head_dim).transpose(1, 2)
    q_nope, q_pe = torch.split(
        q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1
    )

    compressed_kv = self.kv_a_proj_with_mqa(hidden_states)
    compressed_kv, k_pe = torch.split(
        compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1
    )
    k_pe = k_pe.view(bsz, q_len, 1, self.qk_rope_head_dim).transpose(1, 2)
    kv = (
        self.kv_b_proj(self.kv_a_layernorm(compressed_kv))
        .view(bsz, q_len, self.num_heads, self.qk_nope_head_dim + self.v_head_dim)
        .transpose(1, 2)
    )

    k_nope, value_states = torch.split(
        kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1
    )
    kv_seq_len = value_states.shape[-2]
    if past_key_value is not None:
        kv_seq_len += past_key_value.get_usable_length(kv_seq_len, self.layer_idx)
    cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)

    q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)

    query_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
    query_states[:, :, :, : self.qk_nope_head_dim] = q_nope
    query_states[:, :, :, self.qk_nope_head_dim :] = q_pe

    key_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
    key_states[:, :, :, : self.qk_nope_head_dim] = k_nope
    key_states[:, :, :, self.qk_nope_head_dim :] = k_pe
    if past_key_value is not None:
        cache_kwargs = {"sin": sin, "cos": cos}  # Specific to RoPE models
        key_states, value_states = past_key_value.update(
            key_states, value_states, self.layer_idx, cache_kwargs
        )

    attn_weights = (
        torch.matmul(query_states, key_states.transpose(2, 3)) * self.softmax_scale
    )

    if attention_mask is not None:
        attn_weights = attn_weights + attention_mask

    # upcast attention to fp32
    attn_weights = nn.functional.softmax(
        attn_weights, dim=-1, dtype=torch.float32
    ).to(query_states.dtype)
    attn_weights = nn.functional.dropout(
        attn_weights, p=self.attention_dropout, training=self.training
    )
    attn_output = torch.matmul(attn_weights, value_states)
    attn_output = attn_output.transpose(1, 2).contiguous()
    attn_output = attn_output.reshape(bsz, q_len, self.num_heads * self.v_head_dim)
    attn_output = self.o_proj(attn_output)

    if not output_attentions:
        attn_weights = None

    return attn_output, attn_weights, past_key_value

对应如下图例。

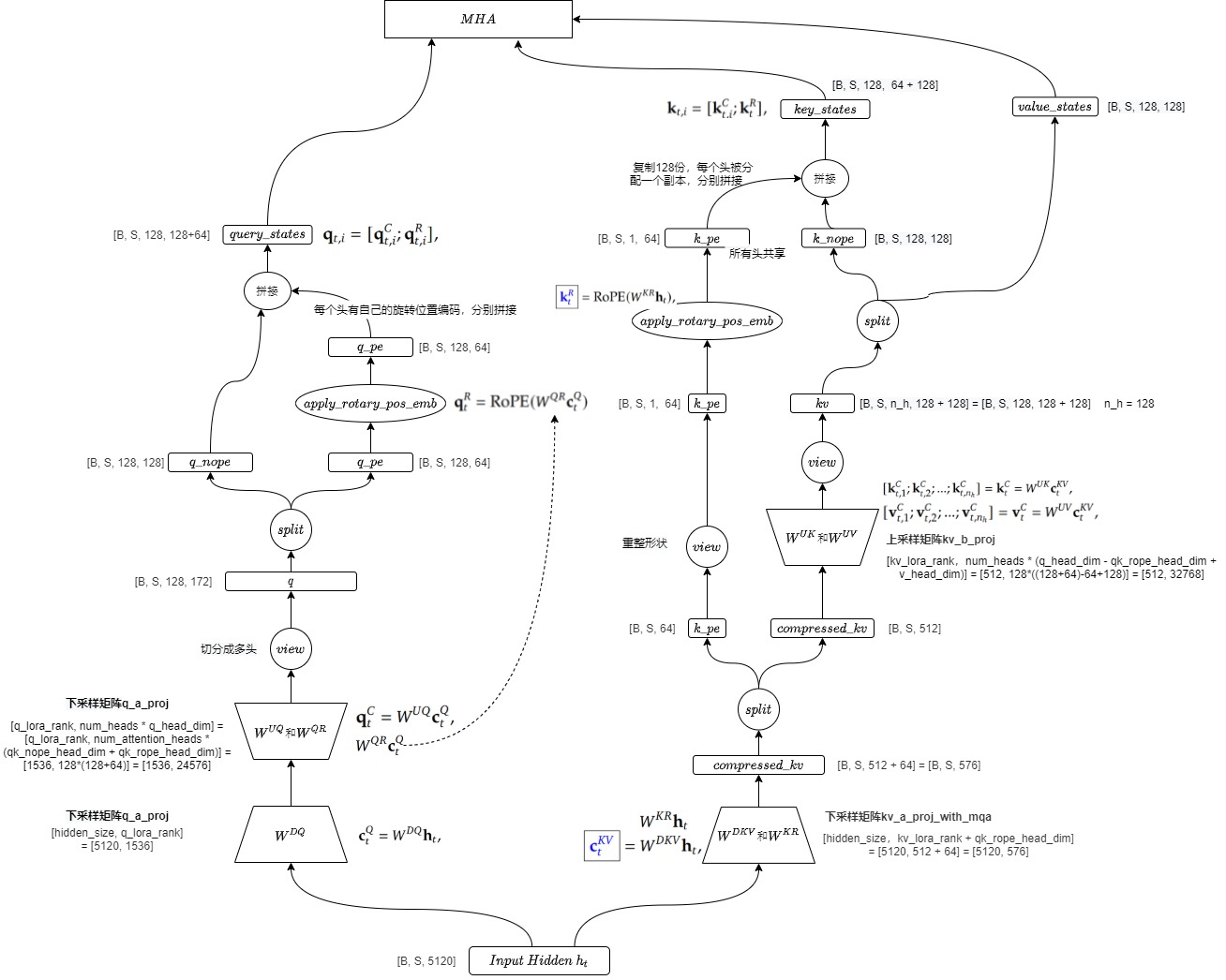
4.7 V3 代码

我们也给出V3代码具体如下。V3中的 native 版本其实并没有节省KV-Cache（甚至还多了存储），V3版本的非native版本是跟论文一致，节省了显存。

native 版本的实现直观、适合学习，但是不适合Decode阶段，因为Decode阶段需要用到KV Cache。针对KV Cache，native 版本的实现有两种选择：

  • ① 缓存 Latent KV。缓存规模小，矩阵运算是 ( b , n h , 1 , d c ) × ( b , 1 , s , d c ) (b,n_h,1,d_c) \times (b,1,s,d_c) (b,nh​,1,dc​)×(b,1,s,dc​)，假定是bfloat16精度，内存读取量是 2 b n h d c + 2 b s d c = 2 b d c ( n h + s ) 2bn_hd_c + 2bsd_c = 2bd_c(n_h+s) 2bnh​dc​+2bsdc​=2bdc​(nh​+s)。但 Latent KV 缓存不能直接送 MHA 计算，还得经过 W U K W^{UK} WUK 和 W U V W^{UV} WUV 的线性映射，这是两个规模不小的矩阵计算，而且每轮都得重复计算。

  • ② 缓存 KV。缓存规模大，不用重复计算，性能好。标准MHA ( b , n h , 1 , d h ) × ( b , n h , s , d h ) (b,n_h,1,d_h) \times (b,n_h,s,d_h) (b,nh​,1,dh​)×(b,nh​,s,dh​)的内存读取量是 2 b n h d h + 2 b n h s d h = 2 b d h n h ( 1 + s ) 2bn_hd_h+2bn_hsd_h = 2bd_hn_h(1+s) 2bnh​dh​+2bnh​sdh​=2bdh​nh​(1+s)。但 MLA 的一大好处就是 KV Cache 压缩，这样显存内能缓存更多 token，支持更大的 batch 和 prefix cache。如果缓存 KV，在显存上对比 MHA 就完全没有优势了。

native 版本最终的选择是方案2。所以，Naive 实现可能会用于 Prefill阶段，但在 Decode 计算时需要更好的计算方法，也就是非native版本。在非native版本最核心的 Attention kernel 计算中，“吸收“模式下 K/V tensor Shape 中不携带 num_attn_heads 信息，计算逻辑转换成了类 MQA 计算，“不吸收”模式下 K/V tensor 仍携带 num_attn_heads，就是MHA计算。

# from: https://github.com/deepseek-ai/DeepSeek-V3/blob/main/inference/model.py
class MLA(nn.Module):
    def __init__(self, args: ModelArgs):
        super().__init__()
        self.dim = args.dim
        self.n_heads = args.n_heads
        self.n_local_heads = args.n_heads // world_size
        # 对应 query 压缩后的隐向量的维度 d'_c
        self.q_lora_rank = args.q_lora_rank # q 压缩后的维度
        # 对应 key-value 压缩后的隐向量维度 d_c
        self.kv_lora_rank = args.kv_lora_rank # kv 压缩后的维度
        # 表示query和key的向量中应用rope部分的维度, $d_h$
        self.qk_nope_head_dim = args.qk_nope_head_dim
        # 对应$d_h^R$， 表示应用了rope的 queries 和 key 的一个 head 的维度。
        self.qk_rope_head_dim = args.qk_rope_head_dim
        # $d_h + d_h^R$, 注意力头大小为非rope部分大小加上rope部分大小
        self.qk_head_dim = args.qk_nope_head_dim + args.qk_rope_head_dim
        self.v_head_dim = args.v_head_dim

        if self.q_lora_rank == 0:
            # 不适用低秩分解，回归到传统MHA
            self.wq = ColumnParallelLinear(self.dim, self.n_heads * self.qk_head_dim)
        else:
            # 其实就是$W^{DQ}$，用来生成$c_t^Q$
            # 下采样矩阵，得到压缩后的q向量
            self.wq_a = Linear(self.dim, self.q_lora_rank)
            self.q_norm = RMSNorm(self.q_lora_rank)
            # $W^{UQ}$
            # 上采样矩阵，用来恢复q向量
            self.wq_b = ColumnParallelLinear(self.q_lora_rank, self.n_heads * self.qk_head_dim)
        # $[W^{DKV}; W^{KR}]$    
        # 下采样矩阵，得到压缩后的kv向量    
        self.wkv_a = Linear(self.dim, self.kv_lora_rank + self.qk_rope_head_dim)
        self.kv_norm = RMSNorm(self.kv_lora_rank)
        # 上采样矩阵，用来恢复kv向量
        # $[W^{UK}; W^{UV}]$
        self.wkv_b = ColumnParallelLinear(self.kv_lora_rank, self.n_heads * (self.qk_nope_head_dim + self.v_head_dim))
        self.wo = RowParallelLinear(self.n_heads * self.v_head_dim, self.dim)
        self.softmax_scale = self.qk_head_dim ** -0.5
        if args.max_seq_len > args.original_seq_len:
            mscale = 0.1 * args.mscale * math.log(args.rope_factor) + 1.0
            self.softmax_scale = self.softmax_scale * mscale * mscale
         
        if attn_impl == "naive": # native模式下，kvcache存储的是没有压缩的数据，大小为d_h + d_h^R, 不但没有节省，反而增加了显存消耗   
            self.register_buffer("k_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.qk_head_dim), persistent=False)
            self.register_buffer("v_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.v_head_dim), persistent=False)
        else:
            # 在非native模式下，存储的是压缩的c，大小为d_c
            self.register_buffer("kv_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.kv_lora_rank), persistent=False)
            self.register_buffer("pe_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.qk_rope_head_dim), persistent=False)

    def forward(self, x: torch.Tensor, start_pos: int, freqs_cis: torch.Tensor, mask: Optional[torch.Tensor]):
        bsz, seqlen, _ = x.size()
        end_pos = start_pos + seqlen
        # 计算q
        if self.q_lora_rank == 0:
            q = self.wq(x)
        else:
            q = self.wq_b(self.q_norm(self.wq_a(x)))
        q = q.view(bsz, seqlen, self.n_local_heads, self.qk_head_dim)
        # 分离nope,rope
        q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
        # 执行RoPE计算
        q_pe = apply_rotary_emb(q_pe, freqs_cis)
        kv = self.wkv_a(x)
        # KV-Cache大小为wkv_a outputdim(self.kv_lora_rank + self.qk_rope_head_dim)
        # 分离KV和K位置编码
        kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
        # 执行RoPE计算
        k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis)
        if attn_impl == "naive":
            q = torch.cat([q_nope, q_pe], dim=-1)
            kv = self.wkv_b(self.kv_norm(kv))
            kv = kv.view(bsz, seqlen, self.n_local_heads, self.qk_nope_head_dim + self.v_head_dim)
            k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
            k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_local_heads, -1)], dim=-1)
            self.k_cache[:bsz, start_pos:end_pos] = k # 存储的是完全没有压缩的k
            self.v_cache[:bsz, start_pos:end_pos] = v # 存储的是完全没有压缩的v
            # score = q^T \times k_cache
            scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bsz, :end_pos]) * self.softmax_scale
        else:
            # 处理KV u-pprojection矩阵
            wkv_b = self.wkv_b.weight if self.wkv_b.scale is None else weight_dequant(self.wkv_b.weight, self.wkv_b.scale, block_size) 
            wkv_b = wkv_b.view(self.n_local_heads, -1, self.kv_lora_rank)
            # q_{nope} = q_{nope} \times W^{UK}
            # q中不需要位置编码的先和K的不需要位置编码的权重相乘
            q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim])
            self.kv_cache[:bsz, start_pos:end_pos] = self.kv_norm(kv) # 保存KV Cache
            self.pe_cache[:bsz, start_pos:end_pos] = k_pe.squeeze(2) # 保存K的位置编码Cache(pe cache)
            # scores = q_{nope}^T \times kv\_cache + q_{pe}^T \times pe\_cache
            scores = (torch.einsum("bshc,btc->bsht", q_nope, self.kv_cache[:bsz, :end_pos]) +
                      torch.einsum("bshr,btr->bsht", q_pe, self.pe_cache[:bsz, :end_pos])) * self.softmax_scale
        if mask is not None:
            scores += mask.unsqueeze(1)
        scores = scores.softmax(dim=-1, dtype=torch.float32).type_as(x)
        if attn_impl == "naive":
            # score \times v_cache
            x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bsz, :end_pos])
        else:
            # u = W^{UV} \times scores \times kv\_cache
            x = torch.einsum("bsht,btc->bshc", scores, self.kv_cache[:bsz, :end_pos])
            # out = W^O \times u
            x = torch.einsum("bshc,hdc->bshd", x, wkv_b[:, -self.v_head_dim:])
        x = self.wo(x.flatten(2))
        return x

具体比对如下图。

0x05 优化代码

DeepSeek代码并没有给出某些功能的具体方案，比如压缩优化和权重吸收。因此，我们主要以章明星老师给出的方案 https://github.com/madsys-dev/deepseekv2-profile/tree/main DeepSeek-V2 高性能推理 (1)：通过矩阵吸收十倍提速 MLA 算子为例进行学习。

5.1 压缩优化

目前V2代码中，Attention中的KV Cache缓存的仍然是全量的key和value（从隐向量又解压缩出来），而并非论文中所说的压缩后的compressed_kv以及k_pe，导致其实没有减少KV Cache的缓存。

主要原因可能是：一方面复用transformers原有的Cache逻辑，方便实验和理解；另一方面这部分应该是训练代码，而推理代码会针对这部分进行优化和改进。

我们可以做如下修改，也将RoPE后的k_pe一并缓存入KV Cache中。

# 将当前位置之前的压缩后的kv（c_t^{kv}）以及应用过rope的k的部分拼接到KV Cache前面
if past_key_value is not None:
    # 得到的应该是
    # compressed_kv: [B, kv_seq_len, d_c]
    # k_pe: [B, 1, kv_seq_len, qk_rope_head_dim]
    compressed_kv, k_pe = past_key_value.update(compressed_kv, k_pe)

章明星老师给出了更详尽的方案。

# CacheCompressed
def forward(self, hidden_states_q: torch.Tensor, q_position_ids: torch.LongTensor, compressed_kv: torch.Tensor):
    ...
    kv_seq_len = compressed_kv.size(1)
    # 对应完整公式的 44 行反过来
    compressed_kv, k_pe = torch.split(
        compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1
    )
    k_pe = k_pe.view(bsz, kv_seq_len, 1, self.qk_rope_head_dim).transpose(1, 2)
    kv = self.kv_b_proj(compressed_kv) \
        .view(bsz, kv_seq_len, self.num_heads, self.qk_nope_head_dim + self.v_head_dim) \
        .transpose(1, 2)
    
    k_nope, value_states = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
    ... 
    
def compress_kv(self, hidden_states_kv: torch.Tensor, kv_position_ids: torch.LongTensor) -> torch.Tensor:
    # return the RoPE'ed & compressed kv
    bsz, kv_seq_len, _ = hidden_states_kv.size()
    compressed_kv = self.kv_a_proj_with_mqa(hidden_states_kv) 
    compressed_kv, k_pe = torch.split(
        compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1
    )
    compressed_kv = self.kv_a_layernorm(compressed_kv)
    k_pe = k_pe.view(bsz, kv_seq_len, 1, self.qk_rope_head_dim).transpose(1, 2)
    cos, sin = self.rotary_emb(k_pe) 
    k_pe = apply_rotary_pos_emb(k_pe, cos, sin, kv_position_ids).view(bsz, kv_seq_len, self.qk_rope_head_dim)
    return torch.cat([compressed_kv, k_pe],dim=-1)

5.2 权重吸收

在计算MLA的时候，仍然需要存储解压后的完整的KV Cache，这很可能引起OOM崩溃。DeepSeek-V2的论文中提出，可以将KV的解压缩矩阵吸收到Q-projection和Out-projection中，从而可以在不解压缩KV Cache的情况下直接计算最终的Attention结果。

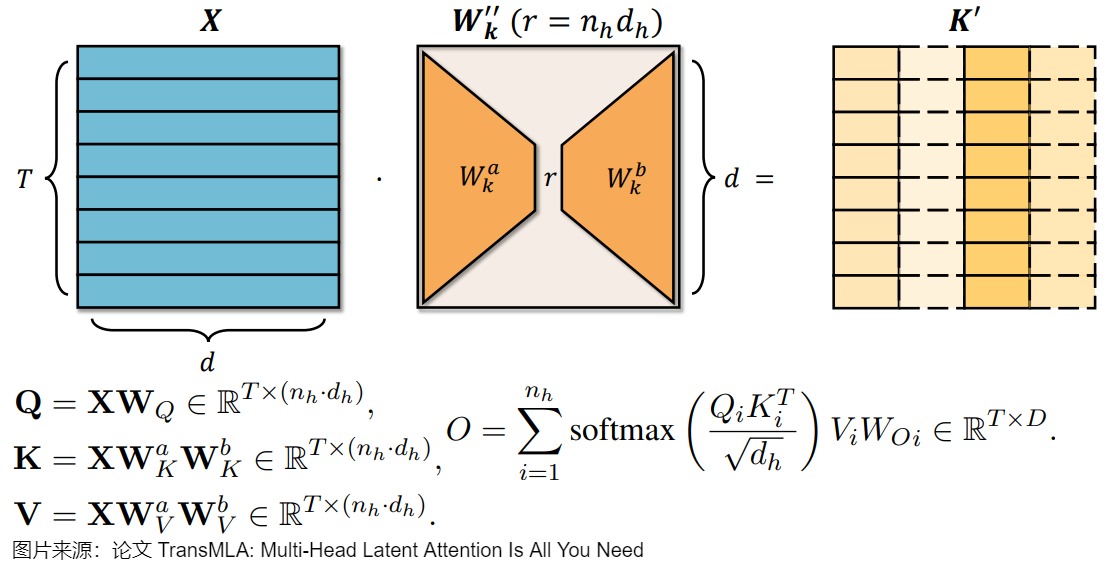
实际上，把权重吸收理解成矩阵乘法交换律更合适。因为实际上是提前将两个参数矩阵乘起来，即把 ( W U Q ) T W U K (W^{UQ})^TW^{UK} (WUQ)TWUK 的计算结果做为新的参数矩阵，然后再跟中间张量乘，在性能上不一定比分开计算更好。

下图分别给出了MHA、MLA和权重吸收的MLA的计算示例。最右侧的两个虚线箭头，显示了在优化的计算过程中，哪些参数矩阵被交换了位置。它们能交换的原因，就是从数学上这样修改是等价的（矩阵乘法交换律）。此时，输入注意力机制的 q、k、v 形状发生了明显的变化。q 的形状由 [ n h × ( d h + d h R ) ] [n_h \times (d_h+d_h^R)] [nh​×(dh​+dhR​)] 变化成了 [ n h × ( d c + d h R ) ] [n_h \times (d_c+d_h^R)] [nh​×(dc​+dhR​)]，k 的形状由 [ n h × ( d h + d h R ) ] [n_h \times (d_h + d_h^R)] [nh​×(dh​+dhR​)] 变化成了 [ n h × ( d c + d h R ) ] [n_h \times (d_c + d_h^R)] [nh​×(dc​+dhR​)]，v 的形状由 d h d_h dh​ 变化成了 d c d_c dc​。这样一来，新的计算过程中只剩下 ① Latent KV 了。原来的 ② KV 就不存在了，变成可以用Latent KV表示。而且实际上 V 也不存在了，因为 V 就是 K 的前 512 维。这其实就是MQA，这实际上就是 FlashMLA 代码库解决的问题。

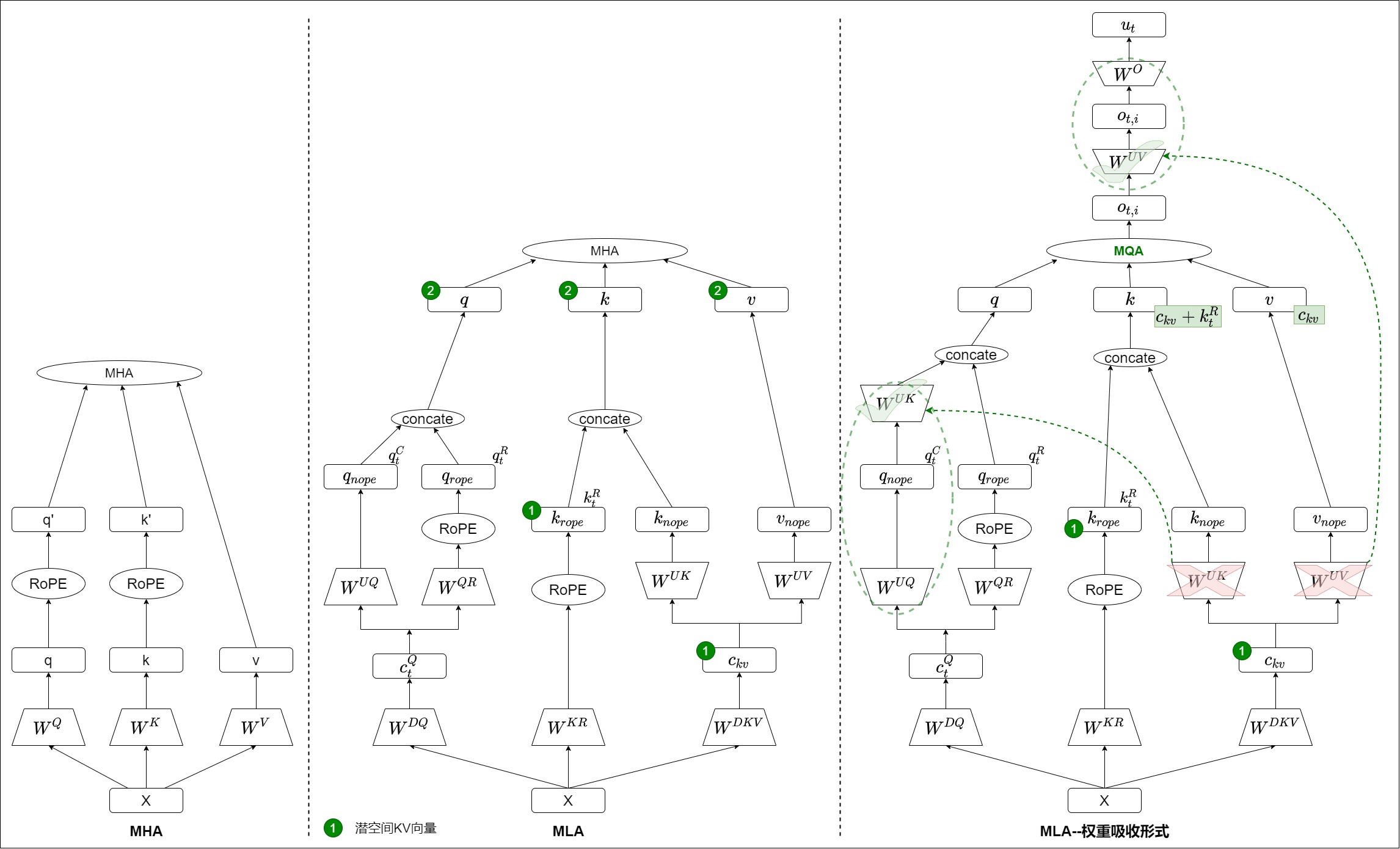
我们接下来依据章老师的代码和文字来继续学习。

5.2.1 absorbed_cache_compressed.py

与论文不同，此处将代码中 kv_b_proj 中属于 K 的部分权重（论文中对应 W U K W^{UK} WUK）吸收进 q_nope（论文中对应 q C q^C qC，而且是在运行时做，非提前吸收）；将代码中 kv_b_proj 中属于 V 的部分权重（论文中对应 W U V W^{UV} WUV）吸收进 attn_out。抽象一点的理解就是，将 Q 也映射到 KV 的低秩空间，然后在低秩空间做完整的 Attention，之后再映射回 Q 的原始空间。

W U K W^{UK} WUK

对于K的吸收，在注意力分数的计算公式中，非RoPE部分可以做如下展开：
q t C ⊤ k t C = ( W U Q c t Q ) ⊤ W U K c t K V = c t Q ⊤ W U Q ⊤ W U K c t K V = ( c t Q ⊤ W U Q ⊤ W U K ) c t K V {q_t^C}^\top k_t^C = (W^{UQ} c_t^Q)^{\top} W^{UK} c_t^{KV} = {c_t^Q}^{\top}{W^{UQ}}^{\top} W^{UK} c_t^{KV} = ({c_t^Q}^{\top}{W^{UQ}}^{\top} W^{UK}) c_t^{KV} qtC​⊤ktC​=(WUQctQ​)⊤WUKctKV​=ctQ​⊤WUQ⊤WUKctKV​=(ctQ​⊤WUQ⊤WUK)ctKV​
也就是说，我们事实上不需要每次都将低维的 c t K V c_t^{KV} ctKV​展开为 k t k_t kt​再计算，而是通过矩阵乘法结合律，直接将 W U K W^{UK} WUK 通过结合律先和左边做乘法，改为计算，避免了解压缩出完整的K矩阵。即将前三者进行计算：
a t t e n t i o n _ w e i g h t s = ( c t Q ⊤ W U Q ⊤ W U K ) c t K V attention\_weights = ({c_t^Q}^{\top}{W^{UQ}}^{\top} W^{UK}) c_t^{KV} attention_weights=(ctQ​⊤WUQ⊤WUK)ctKV​

此外，在原始版本的解压缩的过程中，由于每个token的key都需要与 W U K W^{UK} WUK相乘才能得到，因此计算量较大；矩阵吸收后， W U K W^{UK} WUK只需要对 q t C q_t^C qtC​这一个向量相乘，也大大减少了浮点计算量。

# Absorbed_CacheCompressed
def forward(hidden_states_q: torch.Tensor, q_position_ids: torch.LongTensor, compressed_kv: torch.Tensor):
    ...
    # 从 kv_b_proj 中分离的 W^{UK} 和 W^{UV} 两部分，他们要分别在不同的地方吸收
    kv_b_proj = self.kv_b_proj.weight.view(self.num_heads, -1, self.kv_lora_rank)
    q_absorb = kv_b_proj[:, :self.qk_nope_head_dim,:]
    out_absorb = kv_b_proj[:, self.qk_nope_head_dim:, :]
    
    cos, sin = self.rotary_emb(q_pe)
    q_pe = apply_rotary_pos_emb(q_pe, cos, sin, q_position_ids)
    
    qk_head_dim = self.kv_lora_rank + self.qk_rope_head_dim
    query_states = k_pe.new_empty(bsz, self.num_heads, q_len, qk_head_dim)
    # 此处改变了q_nope的计算顺序，把 W^{UK} 吸收到 W^{UQ}
    query_states[:, :, :, : self.kv_lora_rank] = torch.einsum('hdc,bhid->bhic', q_absorb, q_nope)
    query_states[:, :, :, self.kv_lora_rank :] = q_pe
    
    ...

    attn_weights = nn.functional.softmax(
        attn_weights, dim=-1, dtype=torch.float32
    ).to(q_nope.dtype)
    # 此处改变了attn_output的计算顺序
    attn_output = torch.einsum('bhql,blc->bhqc', attn_weights, compressed_kv)
    attn_output = torch.einsum('bhqc,hdc->bhqd', attn_output, out_absorb)
    attn_output = attn_output.transpose(1, 2).contiguous()
    attn_output = attn_output.reshape(bsz, q_len, self.num_heads * self.v_head_dim)
    attn_output = self.o_proj(attn_output)

除了压缩KV Cache之外，我们还可以观察到上面涉及到的2个矩阵乘法实际上都来到了计算密集的领域，例如对于 torch.einsum('bhqc,blc->bhql', q_nope, compressed_kv) 。由于不同 head 的 q_nope 部分共享了共同的 compressed_kv 部分，实际计算的是 batch_size 个 [head_num * q_len, kv_lora_rank] 和 [past_len, kv_lora_rank] 的矩阵乘法。计算等价于一个 MQA 操作，计算强度正比于 head_num 的也就是 128。因此相比 MHA，吸收后的 MLA 计算强度要大得多，可以更加充分的利用 GPU 算力。

W U V W^{UV} WUV

对于V的吸收，情况稍微复杂。为表述的清楚性，我们采用Einstein求和约定描述该过程

v_t = einsum('hdc,blc->blhd', W_UV, c_t_KV) # (1)
o   = einsum('bqhl,blhd->bqhd', a, v_t)     # (2)
u   = einsum('hdD,bhqd->bhD', W_o, o)       # (3)

# 将上述三式合并，得到总的计算过程
u   = einsum('hdc,blc,bqhl,hdD->bhD', W_UV, c_t_KV, a, W_o)

# 利用结合律改变计算顺序
o_  = einsum('bhql,blc->bhqc', a, c_t_KV) # (4)
o   = einsum('bhqc,hdc->bhqd', o_, W_UV)  # (5)
u   = einsum('hdD,bhqd->bhD', W_o, o)     # (6)
5.2.2 Move Elision

不过，这样还不能完全发挥出MLA的威力。在原始代码中，query_states和key_states会通过拼接RoPE和非RoPE部分得到：

def forward(...):
    ...
    # 更新和拼接历史 KVCache，可以看到这里存储的是展开后的 MHA KVCache
    # 其中 q_head_dim 等于 qk_nope_head_dim + qk_rope_head_dim    
    query_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
    query_states[:, :, :, : self.qk_nope_head_dim] = q_nope
    query_states[:, :, :, self.qk_nope_head_dim :] = q_pe

    key_states = k_pe.new_empty(bsz, self.num_heads, kv_seq_len, self.q_head_dim)
    key_states[:, :, :, : self.qk_nope_head_dim] = k_nope
    key_states[:, :, :, self.qk_nope_head_dim :] = k_pe
    ...

当我们采取了上述优化后，此处的拼接过程会产生大量无用的数据拷贝和广播，同时也会占用大量显存空间导致OOM，而且如果是concat放在框架做，但可能会增加IO，尤其是decode本就是IO瓶颈。而且，先对Latent解压缩再计算，则Attn的计算是一个实打实的Multi Head Attention，会增大计算量。

为此，我们采用MoveElision优化策略，即省略此处的拼接RoPE部分和非RoPE部分的过程，而是直接分别计算量部分的Attention Score并相加（考虑 q t ⊤ k t = q t C ⊤ k t C + q t R ⊤ k t R q_t^\top k_t = {q_t^C}^\top k_t^C + {q_t^R}^\top k_t^R qt⊤​kt​=qtC​⊤ktC​+qtR​⊤ktR​）。即，将 RoPE 部分与 NoPE 部分分别做乘法，然后进行拼接的操作，改为 NoPE 部分 Attention 和 RoPE 部分 Attention 两者结果相加，这样做的好处在于节省了内存搬运操作，这种做法等效于ALiBi。我们具体推导如下。
[ q t , i ⊤ k j , i ] = [ c t Q W U Q ⊤ , q t R ⊤ ] [ W U K c t K V k t R ] = c t Q W U Q ⊤ W U K c t K V + q t R ⊤ k t R [q^{\top}_{t,i}k_{j,i}] = [{c_t^Q}{W^{UQ}}^{\top},q_t^{R^\top}]\begin{bmatrix}W^{UK}c_t^{KV}\\ k_t^R \end{bmatrix} = c_t^Q{W^{UQ}}^{\top}W^{UK}c_t^{KV} + q_t^{R^{\top}}k_t^R [qt,i⊤​kj,i​]=[ctQ​WUQ⊤,qtR⊤​][WUKctKV​ktR​​]=ctQ​WUQ⊤WUKctKV​+qtR⊤​ktR​
具体对应下面代码中的torch.matmul(q_pe, k_pe.transpose(2, 3))这行。即，分开计算了RoPE部分的q和k的注意力计算再求和。标准实现是将加上了 rope 的 q_pe/k_pe 和没加 rope 的 q_nope/k_nope 拼接起来一起。

# Absorbed_CacheCompressed_MoveElision
def forward(...):
    ...
    # qk_head_dim = self.kv_lora_rank + self.qk_rope_head_dim
    # query_states = k_pe.new_empty(bsz, self.num_heads, q_len, qk_head_dim)
    # query_states[:, :, :, : self.kv_lora_rank] = torch.einsum('hdc,bhid->bhic', q_absorb, q_nope)
    # query_states[:, :, :, self.kv_lora_rank :] = q_pe

    # key_states = k_pe.new_empty(bsz, self.num_heads, kv_seq_len, qk_head_dim)
    # key_states[:, :, :, : self.kv_lora_rank] = compressed_kv.unsqueeze(1)
    # key_states[:, :, :, self.kv_lora_rank :] = k_pe

    # attn_weights = torch.matmul(query_states, key_states.transpose(2, 3)) * self.softmax_scale

    # 吸收后 attn_weights 直接基于 compressed_kv 计算不用展开
    attn_weights = torch.matmul(q_pe, k_pe.transpose(2, 3)) + torch.einsum('bhqc,blc->bhql', q_nope, compressed_kv)
    attn_weights *= self.softmax_scale
    ...

代码比对如下：

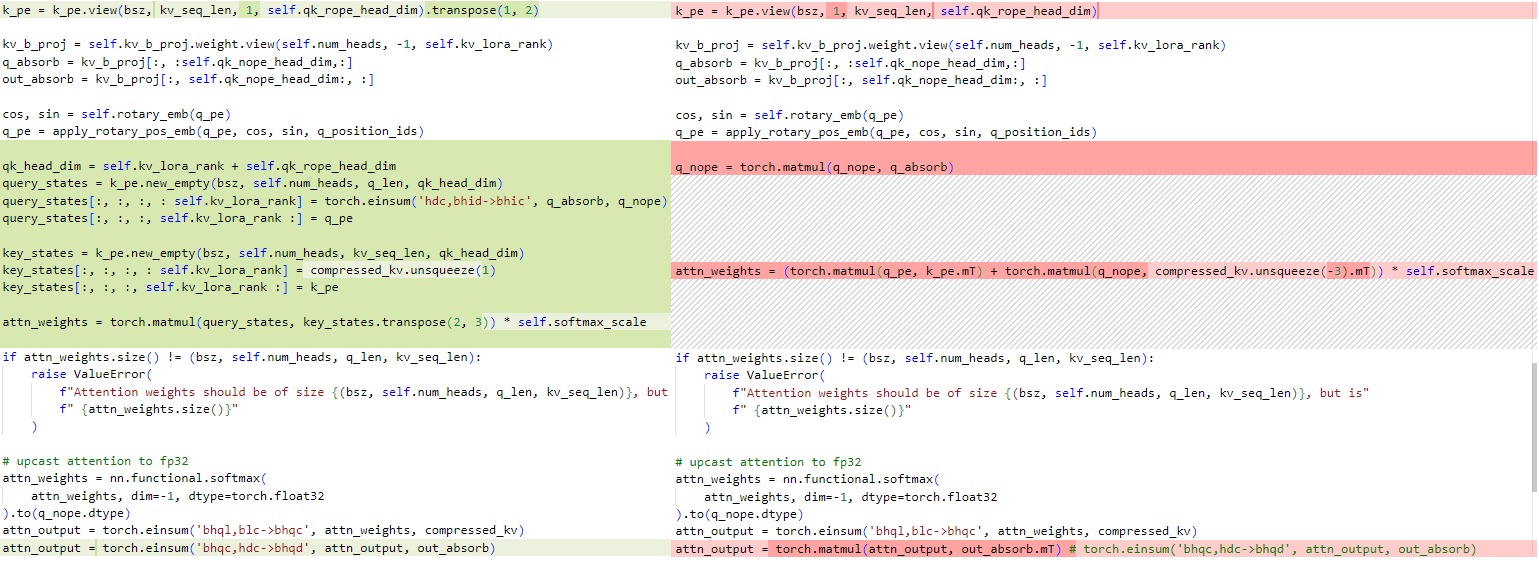
5.2.3 Materializing Projection Matrices

DeepSeek-V2的论文中说：

不过，似乎并没有必要再改变顺序，对模型参数进行预处理，将 W U K W^{UK} WUK与 W U Q W^{UQ} WUQ相乘，以及将 W U V W^{UV} WUV与 W O W^O WO相乘。这是因为， W U K W^{UK} WUK与 W U Q W^{UQ} WUQ相乘后的结果可以视为 H H H个大小为 1536 × 512 1536 \times 512 1536×512的低秩（不超过128）矩阵，而 W U V W^{UV} WUV与 W O W^O WO相乘的结果可以视为 H H H个大小为 5120 × 512 5120 \times 512 5120×512的低秩矩阵。相比用这些特别大的低秩矩阵做投影，明显不如按照低秩分解形式依次相乘来得划算。因此，章老师认为这一步的优化并不是很有必要。

因为假设有矩阵 A[m,k],B[k,n],C[n,l]，B 和 C 为低秩矩阵，依次相乘 A⋅B⋅C 需要的算力： 2mkn+2mnl=2mn⋅(k+l)，而提前合并 D=(B⋅C)，A⋅D 需要的算力：2mkl，当 n⋅(k+l)<kl 时，提前合并低秩矩阵，反而会引入更多计算。而在 LoRA 的推理阶段，之所以能这样做，是因为本身就已经存在一个大的 pre-train weight 的矩阵，因此提前做吸收，不会增加计算量。

具体代码如下：

def forward(self, hidden_states_q: torch.Tensor, q_position_ids: torch.LongTensor, compressed_kv: torch.Tensor):
    '''
    Attention masks and past cache are removed.
    Input: 
    - hidden_states_q: [bsz, q_len, hidden_size]
    - compressed_kv: [bsz, kv_len, kv_lora_rank]
    - position_ids: [bsz, q_len]
    '''
    bsz, q_len, _ = hidden_states_q.size()
    q_b_proj_rope, q_absorbed, out_absorbed = self.get_absorbed_proj()
    q = self.q_a_layernorm(self.q_a_proj(hidden_states_q))
    q_nope = torch.einsum('bqc,hdc->bhqd', q, q_absorbed)
    q_pe = torch.einsum('bqc,hdc->bhqd', q, q_b_proj_rope)
    
    cos, sin = self.rotary_emb(q_pe)
    q_pe = apply_rotary_pos_emb(q_pe, cos, sin, q_position_ids)
    kv_seq_len = compressed_kv.size(1)
    compressed_kv, k_pe = torch.split(
        compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1
    )
    k_pe = k_pe.view(bsz, 1, kv_seq_len, self.qk_rope_head_dim)
    
    attn_weights = (torch.matmul(q_pe, k_pe.mT) + torch.matmul(q_nope, compressed_kv.unsqueeze(-3).mT)) * elf.softmax_scale

    # upcast attention to fp32
    attn_weights = nn.functional.softmax(
        attn_weights, dim=-1, dtype=torch.float32
    ).to(q_nope.dtype)
    attn_output = torch.einsum('bhql,blc->bhqc', attn_weights, compressed_kv)
    attn_output = torch.einsum('bhqc,dhc->bqd', attn_output, out_absorbed)
    return attn_output

5.3 融合算子

另外，如果针对prefill和decode阶段进行不同处理，则在推理的时候Prefill 和Decode 走的逻辑不同。

  • 推理的时候 Prefill 是不做矩阵吸收的（原因是Prefill做矩阵吸收会增加计算量），MLA计算与普通的MHA计算大致相同，唯一的区别在于需要支持q/k和v/o使用不同的head_dim。

  • Decode 是要做矩阵吸收的，矩阵吸收ops 远小于矩阵不吸收。这是因为此时Q的长度是1，原本重复在KV 上做up projection的操作转移到了Q 上，让Q 投影到kv 的latent space 上，Q的长度远小于KV的长度，不需要对KV做重复做up projection。或者说，MLA的主要思路就是通过交换矩阵计算顺序，利用decode阶段query seq_len比较小的特点，优化矩阵计算开销，进而达到只存储Multi-head attention中hidden states cache，而不是key和value两个cache，进而降低一半KVCache存储的目的。

因此Decode阶段需要单独设计高效的融合算子，以便高效地与低秩kv-cache进行attention计算。

权重吸收之后，公式如下：
( p ⋅ ( c k v ⋅ W U V ) ) ⋅ W O = ( p ⋅ c k v ) ⋅ ( W U V ⋅ W O ) = ( s o f t m a x ( q n o p e ⋅ c k v + q p e ⋅ k p e ) ⋅ c k v ) ⋅ W U V ⋅ W O (p \cdot (c_{kv} \cdot W^{UV})) \cdot W^O = (p \cdot c_{kv}) \cdot (W^{UV} \cdot W^O) = (softmax(q_{nope} \cdot c_{kv} + q_{pe} \cdot k_{pe}) \cdot c_{kv}) \cdot W^{UV} \cdot W^O (p⋅(ckv​⋅WUV))⋅WO=(p⋅ckv​)⋅(WUV⋅WO)=(softmax(qnope​⋅ckv​+qpe​⋅kpe​)⋅ckv​)⋅WUV⋅WO
可以用代码描述如下，即可以设计一个MQA算子来实现。

q_pe = W_QR(c_q)
q_nope = W_UQ_UK(c_q)
output = W_UV_O(MQA(q_pe, q_nope, c_kv, k_pe))

FlashAttention最初设计的初衷是减少对softmax矩阵储存的开销，其大小正比于 l q ⋅ l k v l_q \cdot l_{kv} lq​⋅lkv​，占整体I/O的比值为：
r a t i o ( s o f t m a x ) = 1 1 + H k v H q o D L q o + D L k v ratio(softmax) = \frac{1}{1+\frac{H_{kv}}{H_{qo}} \frac{D}{L_{qo}}+\frac{D}{L_{kv}}} ratio(softmax)=1+Hqo​Hkv​​Lqo​D​+Lkv​D​1​

对于推理阶段而言， l q l_q lq​ 其实是非常小的，不融合qk和pv两阶段的计算也能取得不错的效果。但是对于MLA而言，融合是必要的，这是因为：

  • MLA有较大的group ratio： 𝐻 𝑞 𝑜 / 𝐻 𝐾 𝑉 = 128 𝐻_{𝑞𝑜}/𝐻_{𝐾𝑉}=128 Hqo​/HKV​=128 ，会增大softmax的占比。
  • MLA复用了key和value矩阵，因此如果我们不融合两阶段的话，前后两个算子将各自访问一遍KV-Cache，如果硬件的cache不够大的话，带宽利用率将无法超过50%。

5.4 矩阵乘的重排序（增补@2025-04-19）

内容参考：DeepSeek V3推理: MLA与MOE解析 Arthur

具体特点如下：

  • 方案来源：SGlang，应用于DeepSeek-V2。
  • 方案特点：基于矩阵乘法结合律改变计算顺序，从而优化注意力机制计算效率。在解码阶段，能够有效减少计算量。
  • 方案内容：
    • 原始计算顺序： q n o p e k n o p e + q r o p e k r o p e q_{nope}k_{nope} + q_{rope}k_{rope} qnope​knope​+qrope​krope​。其中 q n o p e k n o p e q_{nope}k_{nope} qnope​knope​的计算方式是 q n o p e T ( W U K c ) q^T_{nope}(W^{UK}c) qnopeT​(WUKc)。FLOPs为 2 d c − 1 ) h d n k + ( 2 d − 1 ) h n q n k 2d_c -1)hdn_k + (2d-1)hn_qn_k 2dc​−1)hdnk​+(2d−1)hnq​nk​。
    • 改进顺序为： ( q n o p e T W U K ) c (q^T_{nope}W^{UK})c (qnopeT​WUK)c。FLOPs为 ( 2 d − 1 ) h n q d c + ( 2 d c − 1 ) h n q n k (2d-1)hn_qd_c+(2d_c-1)hn_qn_k (2d−1)hnq​dc​+(2dc​−1)hnq​nk​。

这种改变利用了矩阵乘法的结合律，使得计算可以在不同的维度上进行重组，在解码阶段（ n q = 1 n_q=1 nq​=1 ），优化后的方法可以显著减少计算量。

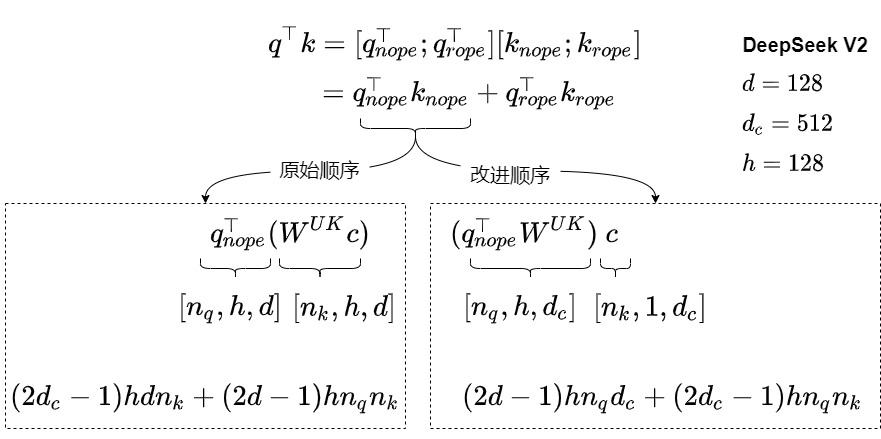
0x06 转换

6.1 GQA

Group Query Attention（GQA）是MHA的一种变体，旨在减少KV缓存的开销。它将查询头分成多个组，每个组共享一个键和值对。这种方法通过减少键和值头的数量来降低KV缓存的大小，但可能会牺牲模型的表达能力。可以将GQA看作是MLA的一种特例。由于GQA是通过复制产生的，而MLA不受这种限制，表达能力更强。

尽管MLA在Deepseek V2/V3/R1中已经证明了其效率和有效性，但许多主要的模型提供商仍然依赖GQA。为了促进MLA的更广泛应用，论文“TransMLA: Multi-Head Latent Attention Is All You Need"提出了TransMLA，这是一种后训练方法，可以将广泛使用的基于GQA的预训练模型（例如LLaMA、Qwen、Mixtral）转换为基于MLA的模型。转换后，模型可以进行额外的训练以增强表达能力，而不会增加KV缓存的大小。

6.1.1 思路

论文首先证明了对于相同的KV缓存开销，MLA的表达能力总是大于GQA。具体来说，任何GQA配置都可以等价地转换为MLA表示，但反之不然。这一结论为将基于GQA的模型转换为基于MLA的模型提供了理论基础。

在等价转换过程中，TransMLA方法首先将GQA中的键矩阵进行复制，以匹配查询头的数量。然后，它将这个复制后的键矩阵分解为两个较小矩阵的乘积，从而得到MLA中的低秩表示。通过这种方法，TransMLA可以在不增加KV缓存大小的情况下，将基于GQA的模型转换为基于MLA的模型。

6.1.2 方案

第一步是复制key矩阵，以匹配查询头的数量。在GQA中，为使标准多头注意力计算时，𝑄和𝐾（以及𝑉）具有相同数量的头，需要对𝐾进行扩展，从 n k n_k nk​个头扩展到 n q n_q nq​个头。这其实也有两种方法。

  • 定义复制因子 𝑠 = 𝑛 𝑞 𝑛 𝑘 𝑠=\frac{𝑛_𝑞}{𝑛_𝑘} s=nk​nq​​（ 𝑛 𝑞 𝑛_𝑞 nq​为𝑄的头数， 𝑛 𝑘 𝑛_𝑘 nk​为𝐾的头数），将𝐾按列划分为 𝑛 𝑘 𝑛_𝑘 nk​个块 𝐾 ( 𝑖 ) 𝐾^{(𝑖)} K(i)，通过将每个 𝐾 ( 𝑖 ) 𝐾^{(𝑖)} K(i)复制𝑠次并连接，得到扩展矩阵𝐾′。具体见下图(a)。
  • 另一种方法是将复制操作移到参数侧（其实也是使用MHA替代GQA的方法），即在计算K之前，先复制投影矩阵 W K W_K WK​。先将 𝑊 𝐾 𝑊_𝐾 WK​按列拆分为 𝑛 𝑘 𝑛_𝑘 nk​个部分 𝑊 𝐾 ( 𝑖 ) 𝑊_𝐾^{(𝑖)} WK(i)​，然后复制每个 𝑊 𝐾 ( 𝑖 ) 𝑊_𝐾^{(𝑖)} WK(i)​ 𝑠次并连接，形成新的投影矩阵 𝑊 𝐾 ′ 𝑊'_𝐾 WK′​，再应用 𝑊 𝐾 ′ 𝑊'_𝐾 WK′​到𝑋直接得到 𝐾 ′ = 𝑋 𝑊 ′ 𝐾 𝐾′=𝑋𝑊′_𝐾 K′=XW′K​，此方法与先计算𝐾再复制其头在数学上是等效的。具体见下图(b)。

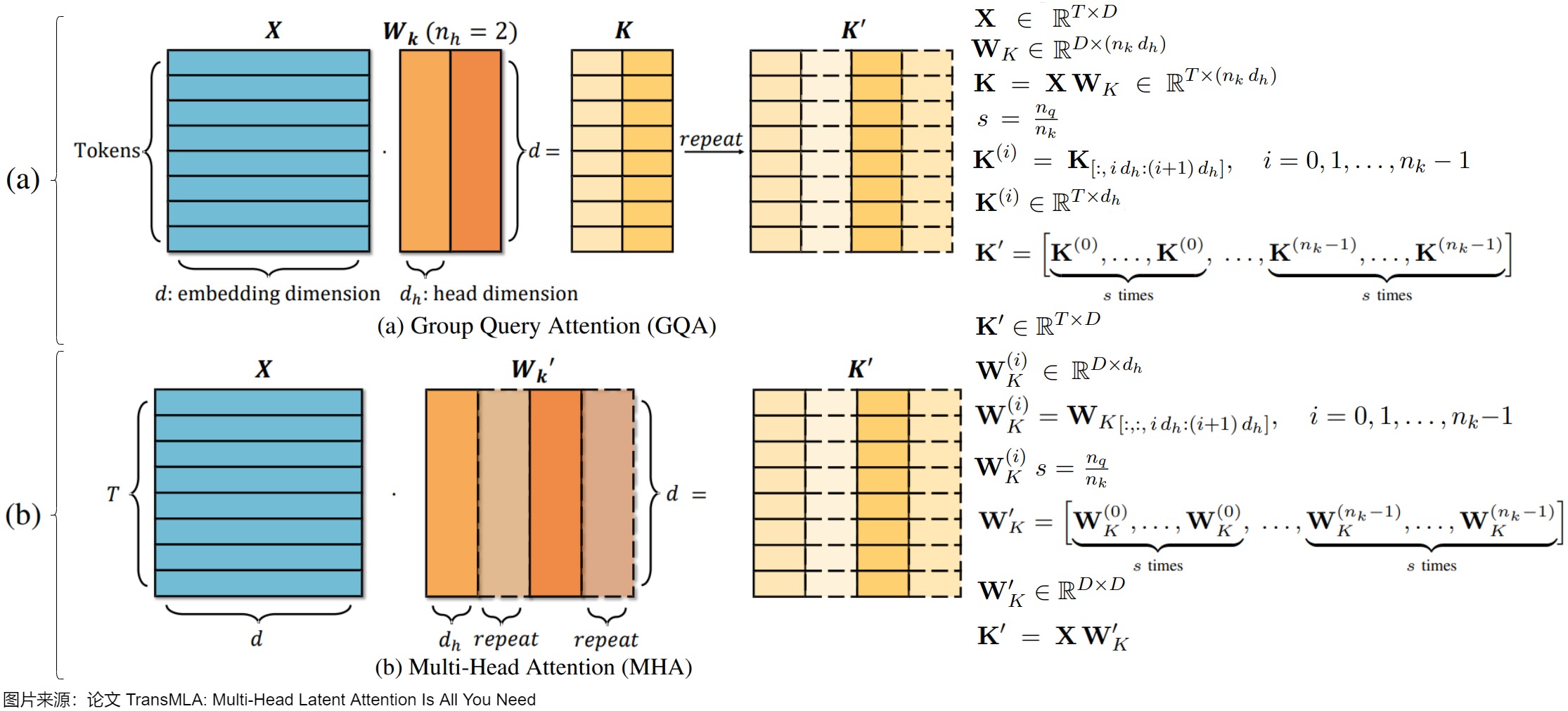
由于 𝑊 𝐾 ′ 𝑊'_𝐾 WK′​由复制 𝑊 𝐾 𝑊_𝐾 WK​形成，其自由度最多为 𝑛 𝑘 𝑑 h 𝑛_𝑘𝑑_ℎ nk​dh​，因此它的秩最多为 𝑛 𝑘 𝑑 h 𝑛_𝑘𝑑_ℎ nk​dh​。为了更正式地理解这一点，通过奇异值分解（SVD）对 𝑊 𝐾 ′ 𝑊'_𝐾 WK′​进行分解： 𝑊 𝐾 ′ = 𝑈 𝐾 𝑆 𝐾 𝑉 𝐾 ⊤ 𝑊'_𝐾=𝑈_𝐾𝑆_𝐾𝑉_𝐾^⊤ WK′​=UK​SK​VK⊤​ ，其中 𝑈 𝐾 𝑈_𝐾 UK​和 𝑉 𝐾 𝑉_𝐾 VK​是𝐷×𝐷正交矩阵， 𝑆 𝐾 𝑆_𝐾 SK​是包含奇异值的𝐷×𝐷对角矩阵。只有前 n k d h n_kd_h nk​dh​（或更少）的奇异值可能是非零的。因此，可以截断SVD，只保留前 r 个奇异值，其中$ r \le n_kd_h 。则 。则 。则𝑊’_𝐾=𝑊_𝐾𝑎𝑊_𝐾𝑏 且 且 且𝐾′=𝑋𝑊_𝐾𝑎𝑊_𝐾𝑏$ 。这样就将GQA的“重复KV”方案解释为类似MLA的低秩分解形式，在实际缓存时，仅需存储低秩表示 𝑋 𝑊 𝐾 𝑎 𝑋𝑊_𝐾^𝑎 XWKa​，在注意力计算时通过乘以 𝑊 𝐾 𝑏 𝑊_𝐾^𝑏 WKb​恢复完整维度，增强了模型的表现力。

6.2 MHA

如何使原本为 MHA 训练的 LLMs（如 Llama）快速适应 MLA 进行推理，而无需从头开始预训练，既具有意义又充满挑战。论文“Towards Economical Inference: Enabling DeepSeek’s Multi-Head Latent Attention in Any Transformer-based LLMs” 第一种数据高效的微调方法MHA2MLA，用于*从MHA转换到MLA。该方法包含两个关键组件：

  • 对于partial-RoPE，论文从对注意力分数贡献较小的查询和键的维度中去除 RoPE。

  • 对于低秩近似，论文基于键和值的预训练参数引入联合SVD近似。

这些精心设计的策略使 MHA2MLA 仅使用极少部分（3‰至 6‰）的数据就能恢复性能，显著降低推理成本，同时能与 KV 缓存量化等压缩技术无缝集成。

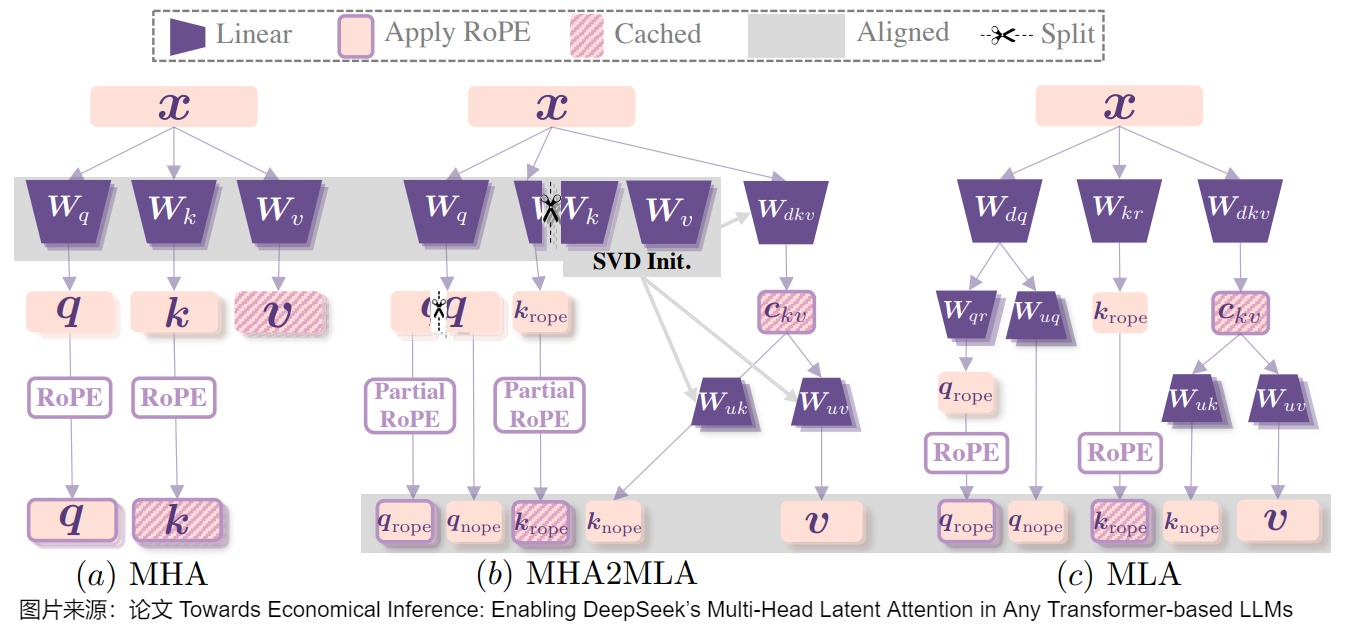
6.2.1 partial-RoPE

为实现从标准 MHA 到 MLA 的迁移，论文提出 partial-RoPE 微调策略，从目标比例的维度中去除 RoPE 并转换为 NoPE。

MHA

MHA 的 Full-RoPE 通过特定频率的旋转将位置信息编码到查询和键中，具体如下图所示。

拆解

MLA中， k i k_i ki​由 [ k i , n o p e ; k i , r o p e ] [k_{i,nope};k_{i,rope}] [ki,nope​;ki,rope​]组成，所以我们首先需要把MHA的 k i , r o p e k_{i,rope} ki,rope​也分解成这样的无RoPE编码和有RoPE两部分。

DeepSeek的MLA里面其实是在原始的每个head的不使用RoPE编码 d h d_h dh​维度上，再增加一个使用RoPE编码的 d h R d_h^R dhR​维度。但是我们现在只能把全长为 d h d_h dh​维度的 k i , r o p e k_{i,rope} ki,rope​进行拆解，把里面 d r , d r ≪ d h d_r,dr \ll d_h dr​,dr≪dh​部分做RoPE编码。也就是 r = d r 2 r=\frac{d_r}{2} r=2dr​​长度的2D子空间做旋转编码。

在注意力计算中，并非所有维度上的旋转位置编码（RoPE）都对结果有同等的贡献。Partial-RoPE 技术通过去除对结果贡献较小的维度上的 RoPE，减少了冗余计算。这就像是在一场考试中，抓住重点知识进行复习，避免在一些无关紧要的知识点上浪费时间。通过这种方式，Partial-RoPE 技术在不影响模型性能的前提下，有效提升了计算效率。

在从 Full-RoPE 转换到 Partial-RoPE 时，我们选择哪一部分子空间来做旋转编码呢？论文提出四种策略（主要是依据旋转的频率）来旋转 RoPE 编码的子空间。

  • 高频保留：保留 r 个旋转最快（高频）的子空间，即位置最靠前的个2D子空间。
  • 低频保留：保留 r 个旋转最慢（低频）的子空间。
  • 均匀采样：选择间隔相等的 r 个子空间，即不管是高频还是低频，按照等距离采样，这样高低频都分别有一部分。
  • 根据每个头2-norm贡献选择（Head-wise 2-norm Contribution）：根据每个头中各子空间的 2-norm分数对所有子空间进行排序，选择前 r 个。第 r 个频率子空间对最终的attention logits的贡献有上界。

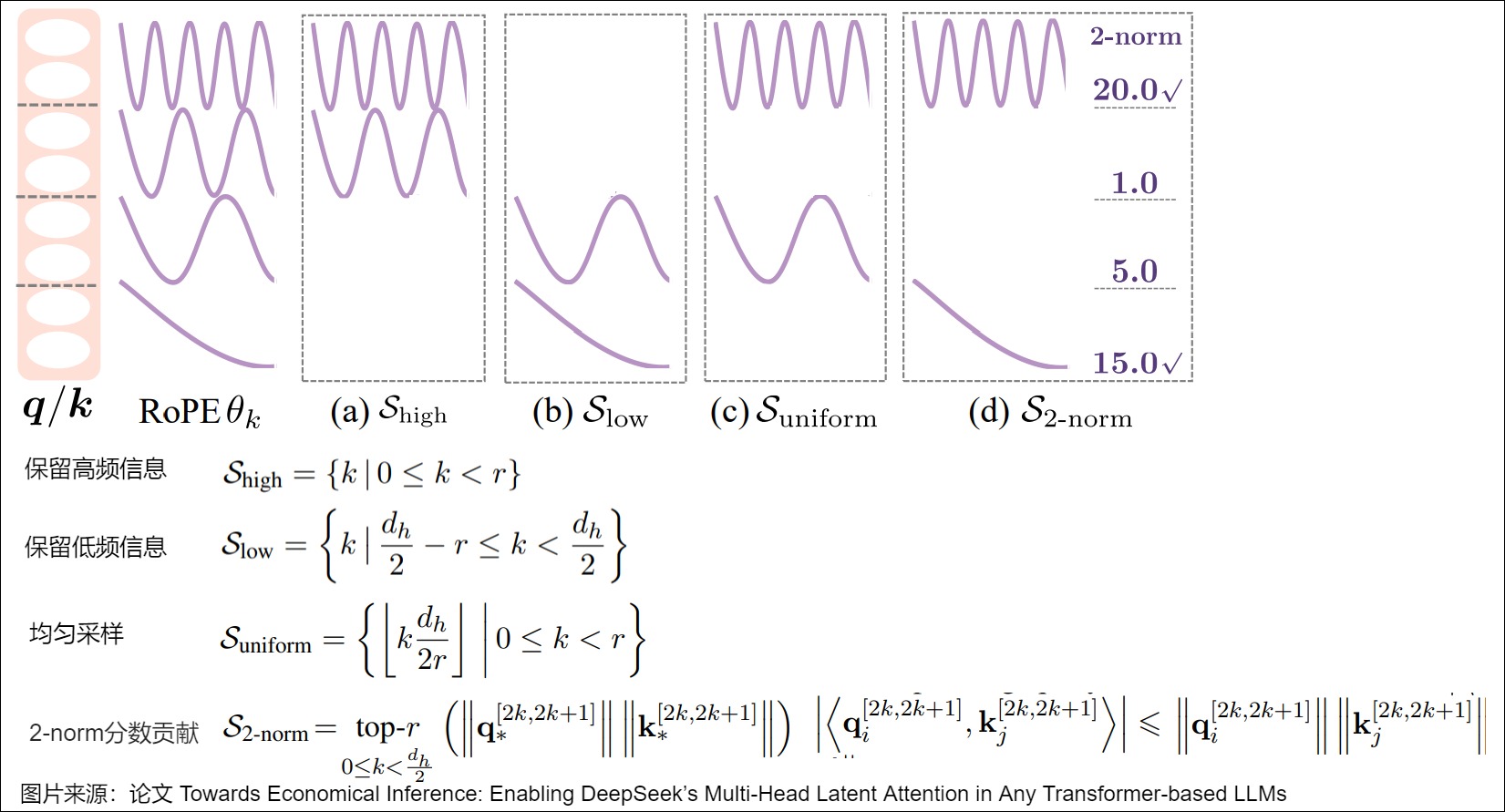
选择好了 d h d_h dh​维度中的 d r d_r dr​维度做RoPE位置编码，剩下的 d h − d r d_h - d_r dh​−dr​部分我们就要当成当成MLA中的无位置编码部分，也就是 q n o p e q_{nope} qnope​。但是要注意DeepSeek的MLA中这部分维度是 d h d_h dh​，我们这里是 d h − d r d_h - d_r dh​−dr​。

6.2.2 低秩近似

MHA中的 k i = W k x i , v i = W v x i k_i = W_kx_i,v_i=W_vx_i ki​=Wk​xi​,vi​=Wv​xi​。我们已经使用上面的四种方法之一找到了需要做RoPE的部分，也就可以把 W k W_k Wk​对应的部分取出来得到 W K R W^{KR} WKR。

我们也把 W k W_k Wk​中对应非RoPE的部分参数提取出来：
k i , n o p e = W k , n o p e x i v i , n o p e = W v , n o p e x i k_{i,nope} = W_{k,nope}x_i \\ v_{i,nope} = W_{v,nope}x_i ki,nope​=Wk,nope​xi​vi,nope​=Wv,nope​xi​
我们的目标是从 W k , n o p e , W v , n o p e W_{k,nope},W_{v,nope} Wk,nope​,Wv,nope​中构造出MLA中的 W D K V W^{DKV} WDKV。

从 Full RoPE 转换到 Partial RoPE 后，为得到 MLA 中 KV 缓存的第二个组件 c i , k v c_{i,kv} ci,kv​，论文提出两种基于SVD的策略：解耦 SVD和联合 SVD，具体参见下图。

  • 解耦 SVD（ S V D s p l i t SVD_{split} SVDsplit​）：分别对 W k , n o p e W_{k,nope} Wk,nope​和 W n W_n Wn​进行截断 SVD 分解，分配 d k v / 2 d_{kv}/2 dkv​/2个维度给每个矩阵。
  • 联合 SVD（ S V D j o i n t SVD_{joint} SVDjoint​）：为保留 K n o p e K_{nope} Knope​和V之间的交互，对连接矩阵 [ W k , n o p e , W v ] [W_{k,nope},W_v] [Wk,nope​,Wv​]进行联合分解。这种分解方式更加贴合MLA的标准格式。

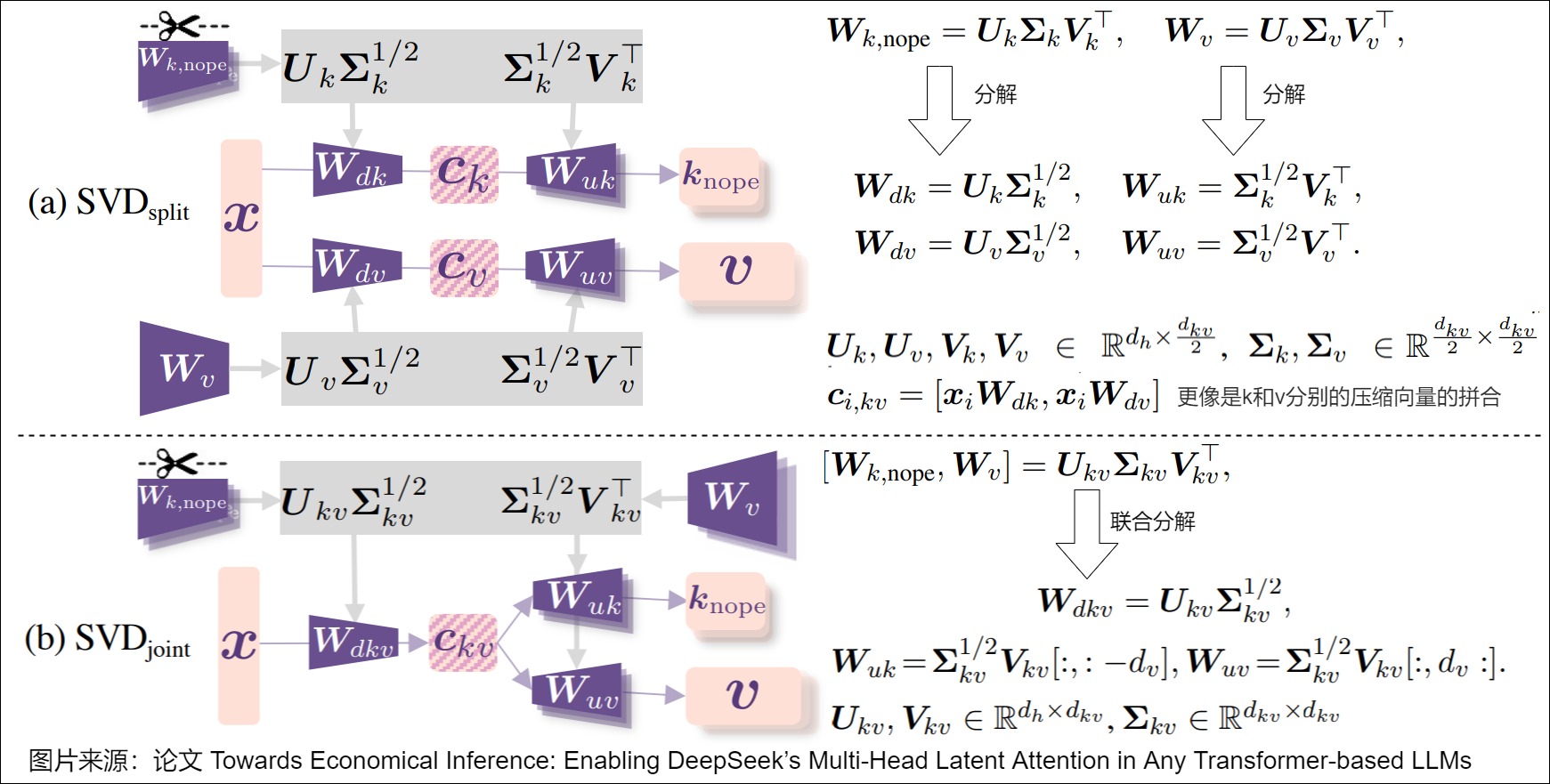
到这里，我们就处理完了key和value部分。query部分并不像DeepSeek里面的MLA一样再做低秩分解，而是把得到的query对应key中的nope和rope部分也分解成两部分。

0xEE 个人信息

★★★★★★关于生活和技术的思考★★★★★★

微信公众账号：罗西的思考

如果您想及时得到个人撰写文章的消息推送，或者想看看个人推荐的技术资料，敬请关注。

在这里插入图片描述

0xFF 参考

DP MLA For DeepSeek In Sglang 是小肖啊

DeepSeek V3, R1, Janus-Pro系列模型方法解读 榴莲酥

【LLM算法】MLA 技术在 DeepSeek-R1 大显神通，清华 TransMLA 将 GQA 一键转换成 MLA SmartMindAI

首个参数高效微调框架：在任何LLMs中使用DeepSeek的MLA AcademicDaily00 [AcademicDaily](javascript:void(0)😉

【LLM算法】MLA 技术在 DeepSeek-R1 大显神通，清华 TransMLA 将 GQA 一键转换成 MLA SmartMindAI

DeepSeekV2之MLA(Multi-head Latent Attention)详解 一滴水的使命

DeepSeek模型解读:Scaling Law,MLA,MoE JMXGODLZ

还在用MHA？MLA来了DeepSeek-v2的MLA的总结和思考 rainbow

一文通透DeepSeek-V2(改造Transformer的中文模型)：详解MoE、GRPO、MLA v_JULY_v

DeepSeekV2之MLA(Multi-head Latent Attention)详解 一滴水的使命

大模型KV Cache节省神器MLA学习笔记（包含推理时的矩阵吸收分析） BBuf

浅读 DeepSeek-V2 技术报告 AGI 梦工厂

用PyTorch从零开始编写DeepSeek-V2 Deephub

图解Mixtral 8 * 7b推理优化原理与源码实现 猛猿

从MHA到MLA看Attention优化：谈谈DeepSeek拼多多级的推理价格 扎波特的橡皮擦 [zartbot](javascript:void(0)😉

继续谈谈MLA以及DeepSeek-MoE和SnowFlake Dense-MoE 扎波特的橡皮擦 [zartbot](javascript:void(0)😉

关于 MHLA（Multi-Head Latent Attention）的一些分析 Zhengxiao Du

[LLM底座] 关于DeepSeek-V2中的MLA（含代码） 莫冉

deepseek-v2 MLA深度解析 单字卓

Deepseek-V2技术详解 队长

如何看待 DeepSeek 发布的 MoE 大模型 DeepSeek-V2？ 郑华滨

缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA 苏剑林

DeepSeek-V2 高性能推理 (1)：通过矩阵吸收十倍提速 MLA 算子 ZHANG Mingxing

速读 deepseek v2（一） —— 理解MLA Bruce 仗剑走天涯

还在用MHA？MLA来了DeepSeek-v2的MLA的总结和思考 rainbow

如何看待 DeepSeek 发布的 MoE 大模型 DeepSeek-V2？ - 知乎 (zhihu.com)

Deepseek-V2技术报告解读！全网最细！ (qq.com) [包包算法笔记](javascript:void(0)😉 2

DeepSeek-V2高性能推理优化笔记：MLA优化 madsys-dev

GQA 论文阅读以及相关的思考 clvsit

LLM 加速技巧：Muti Query Attention deephub

大模型基础｜注意力机制｜MHA｜稀疏｜MQA｜GQA 养生的控制人

Attention优化：Flash Attn和Paged Attn，MQA以及GQA miangangzhen

从头开始编写 LoRA 代码

大模型轻量级微调（LoRA）：训练速度、显存占用分析 绝密伏击

MLKV：跨层 KV Cache 共享，降低内存占用 AI闲谈

继续谈谈MLA以及DeepSeek-MoE和SnowFlake Dense-MoE 扎波特的橡皮擦 [zartbot](javascript:void(0)😉

【深度学习】DeepSeek核心架构-MLA：剖析低秩联合压缩优化KV缓存、提升推理效率的技术细节 赵南夏 [南夏的算法驿站](javascript:void(0)😉

DeepSeek-R1模型架构深度解读（二）MLA [AI算法之道](javascript:void(0)😉

SGLang DP MLA 特性解读 BBuf [GiantPandaCV](javascript:void(0)😉

【LLM论文详解】MLA 技术在 DeepSeek-R1 大显神通，清华 TransMLA 将 GQA 一键转换成 MLA AI-PaperDaily [AI-PaperDaily](javascript:void(0)😉

TransMLA: Multi-Head Latent Attention Is All You Need

SGLang DP MLA 特性解读 BBuf [GiantPandaCV](javascript:void(0)😉

从代码角度学习和彻底理解 DeepSeek MLA 算法 chaofa用代码打点酱油

全网最细！DeepSeekMLA 多头隐变量注意力：从算法原理到代码实现 懂点AI事儿

deepseek技术解读(1)-彻底理解MLA（Multi-Head Latent Attention） 姜富春

[代码学习]deepseek-v2的inference code学习-MLA-part 1 迷途小书僮

[代码学习]deepseek-v2的inference code学习-MLA -part 3 迷途小书僮

[代码学习]deepseek-v2的inference code学习-MLA -part 4 迷途小书僮

[代码学习]deepseek-v2的inference code学习-MLA -part 2 迷途小书僮

缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA 苏剑林

DeepSeek开源FlashMLA之际从原理到代码详解MLA 杜凌霄 [探知轩](javascript:void(0)😉

首个参数高效微调框架：在任何LLMs中使用DeepSeek的MLA [AcademicDaily](javascript:void(0)😉

如何把预训练好的模型中的MHA变为MLA？ 杜凌霄 [探知轩](javascript:void(0)😉

终于把 deepseek 中的多头潜在注意力机制搞懂了！！ 程序员小寒 [程序员学长]

DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model

DeepSeek-V2 高性能推理 (1)：通过矩阵吸收十倍提速 MLA 算子

FlashInfer中DeepSeek MLA的内核设计

细说DeepSeek MLA矩阵消融 formath 2025-02-24

sglang mla 代码解析 hcy

DP MLA For DeepSeek In Sglang 是小肖啊

SGLang DP MLA 特性解读 BBuf

DeepSeek V2/V3中的MLA和Matrix Absorption ariesjzj

FlashInfer中DeepSeek MLA的内核设计 yzh119

终于把 deepseek 中的多头潜在注意力机制搞懂了！！ 程序员小寒 [程序员学长](javascript:void(0)😉

DeepSeek 开源周第一天开源的项目 FlashMLA，有哪些亮点值得关注？ SIY.Z

大模型KV Cache节省神器MLA学习笔记（包含推理时的矩阵吸收分析）

Qwen架构改造成Deepseek，再复现R1计划 孟繁续

DeepSeek V2 “多头潜在注意力”论文解读 (上) 大模型咖啡时间

Deepseek MLA 一定要做吸收吗？ 代码搬运工

DeepSeek V3推理: MLA与MOE解析 Arthur

DeepSeek MLA引发的一些记忆碎片 YyWangCS

谈谈深度学习性能优化中的矩阵计算顺序 YyWangCS

[Deepseek v3技术报告学习] 1.MLA Duludulu

attention中的concat能不能换成相加？ Zhai Feiyue

sglang mla 代码解析 hcy

MLA 实现理解 大卫

SGLang MLA 实现解析 BBuf

DeepSeek V3推理: MLA与MOE解析 Arthur

理解 FlashMLA 在 DeepSeek MLA 计算过程中的位置和作用 solrex [边际效应]

MLA 吸收之谜 拉航母的小朱

MLA原理介绍（极简版） opter

DeepSeek-V3/R1推理效率分析(v0.17) zartbot

DeepSeek V3/R1 推理效率分析（2）: DeepSeek 满血版逆向工程分析 Han Shen

DeepSeek V3/R1 推理效率分析（3）：Decode 配置泛化讨论 Han Shen

DeepSeek V3/R1 推理效率分析（1）：关于DeepSeek V3/R1 Decoding吞吐极限的一些不负责任估计 Han Shen

MoE Inference On AnyScale MoE-On-AnyScale

基于 chunked prefill 理解 prefill 和 decode 的计算特性 Chayenne Zhao

LLM PD 分离背后的架构问题 极客博哥

deepseek MLA推理优化 屈屈臣氏

DeepSeek-V3 MTP 工程实现思考 极客博哥

一点浅见：deepep 为什么快？ 云开

prefill 和 decode 该分离到不同的卡上么？ Chayenne Zhao

[1. deepseek模型学习笔记](https://developnotes.readthedocs.io/zh-cn/latest/deepseek.html#id1) 李伟华

DeepSeek-V3 (671B) 模型参数量分解计算 ZihaoZhao

vLLM 深度解析：Deekseek and vLLM -1 stephenxi

DeepSeek MLA在SGLang中的推理过程及代码实现 榴莲酥

MHA->MQA->GQA->MLA的演进之路 假如给我一只AI

The Annotated Transformer https://nlp.seas.harvard.edu/2018/04/03/ention.html
Attention Is All You Need https://arxiv.org/pdf/1706.03762.pdf

Fast Transformer Decoding: One Write-Head is All You Need https://arxiv.org/pdf/1.02150.pdf

https://www.researchgate.net/figure/led-dot-product-self-attention-mechanism_fig1_363923096

GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints https://arxiv.org/pdf/5.13245.pdf

How Attention works in Deep Learning: understanding the attention mechanism in sequence models https://theaisummer.com/ention/

A simple overview of RNN, LSTM and Attention Mechanism https://medium.com/swlh/imple-overview-of-rnn-lstm-and-attention-mechanism-9e844763d07b

https://pytorch-forecasting.readthedocs.io/en/latest/_modules/pytorch_forecasting/models/temporal_fusion_transformer/_modules.html#ScaledDotProductAttention

浅谈Transformer的初始化、参数化与标准化 https://spaces.ac.cn/archives/0

https://theaisummer.com/self-attention/ ps://theaisummer.com/self-attention/

https://zhuanlan.zhihu.com/p/626820422 https://zhuanlan.zhihu.com/p/626820422
Are Sixteen Heads Really Better than One? https://arxiv.org/pdf/5.10650.pdf

This post is all you need（上卷）——层层剥开Transformer https://zhuanlan.zhihu.com/p/420820453

The Illustrated Transformer https://jalammar.github.io/ustrated-transformer/

Multi-Query Attention is All You Need https://blog.fireworks.ai/multi

DeepSeek MLA的序列并行和张量并行 YyWangCS

DP MLA For DeepSeek In Sglang 是小肖啊

SGLang MLA 实现解析 BBuf

Multi-Head Latent Attention (MLA) 详细介绍（来自Deepseek V3的回答） 银翼的魔朮师

MLA机制原理及代码研究 zrq96

DeepSeek面试通关（1）｜MLA如何让推理效率飙升200%？ 丁师兄大模型

DeepSeek-V2 MLA KV Cache 真的省了吗？ 沉积岩

【Deepseek技术原理】第一篇：深度剖析和图解模型结构MLA 罗辑

网站公告

今日签到

点亮在社区的每一天
去签到

热门文章

最新发布