一、冒泡排序(Bubble Sort)
1. 原理:
- 比较相邻元素,若顺序错误(如升序时前一个大于后一个)则交换。
- 一趟下来可将最大值(或最小值)移到数组末尾(或开头)。
2. 代码示例(Java):
public class BubbleSort {
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换arr[j]和arr[j + 1]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int[] arr = {64, 34, 25, 12, 22, 11, 90};
bubbleSort(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
3. 复杂度及稳定性:
- 时间复杂度:O(N^2),其中N 是数组长度,最坏和平均情况都是比较和交换接近N^2 次。
- 空间复杂度:O(1),仅使用了常数级额外空间。
- 稳定性:稳定,因为交换是相邻元素,相同值元素相对顺序不变。条件判断用 > 而非 >= 保证稳定性,相等时不交换。
二、插入排序(Insertion Sort)
1. 原理:
- 把数组分为有序区间和无序区间,初始时有序区间为空,无序区间为整个数组。
- 每次从无序区间取一个元素,插入到有序区间合适位置,类似玩牌整理手牌。
2. 代码示例(Java):
public class InsertionSort {
public static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6};
insertionSort(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
3. 复杂度及稳定性:
- 时间复杂度:O(N^2),最坏情况每个元素都要移动N 次。
- 空间复杂度:O(1),仅用少量额外空间。
- 稳定性:稳定,插入时相同元素相对顺序不变。
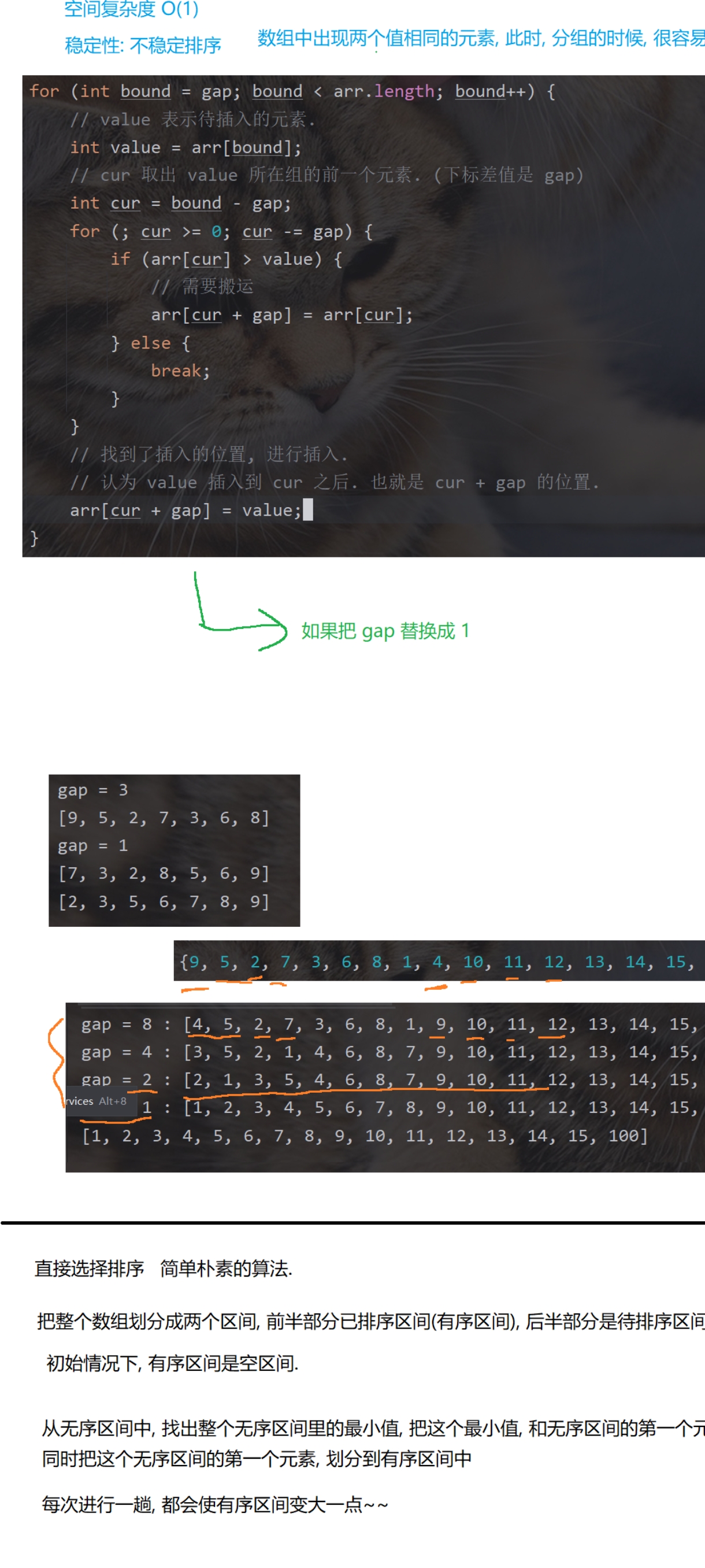
三、希尔排序(Shell Sort)
1. 原理:
- 分组进行插入排序,引入 gap 概念, gap 表示同组元素间隔及分组数。
- 先按较大 gap 分组排序,逐渐减小 gap ,最后 gap 为1时相当于普通插入排序。
2. 代码示例(Java):
public class ShellSort {
public static void shellSort(int[] arr) {
int n = arr.length;
for (int gap = n / 2; gap > 0; gap /= 2) {
for (int i = gap; i < n; i++) {
int temp = arr[i];
int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
arr[j] = arr[j - gap];
}
arr[j] = temp;
}
}
}
public static void main(String[] args) {
int[] arr = {12, 34, 54, 2, 23, 65, 3, 1, 99};
shellSort(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
3. 复杂度及稳定性:
- 时间复杂度:最坏O(N^2),平均复杂度取决于 gap 序列选择。
- 空间复杂度:O(1)。
- 稳定性:不稳定,分组排序时相同值元素可能在不同组,相对顺序可能改变。
四、直接选择排序(Simple Selection Sort)
1. 原理:
- 将数组分为有序区间和无序区间,初始有序区间为空。
- 每次从无序区间找最小值,与无序区间第一个元素交换,使有序区间扩大。
2. 代码示例(Java):
public class SelectionSort {
public static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// 交换arr[i]和arr[minIndex]
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
public static void main(String[] args) {
int[] arr = {64, 25, 12, 22, 11};
selectionSort(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
3. 复杂度及稳定性:
- 时间复杂度:O(N^2),需进行N - 1 趟,每趟找最小值最多比较N - i 次。
- 空间复杂度:O(1)。
- 稳定性:不稳定,交换时相同值元素顺序可能改变。
五、堆排序(Heap Sort)
1. 原理:
- 先建大堆(升序排序时),即让数组满足堆性质(父节点大于子节点)。
- 把堆顶元素(最大值)与待排序区间最后一个元素交换,将最大值移到已排序区间。
- 对新堆顶向下调整,重复直到堆大小为1。
2. 代码示例(Java):
public class HeapSort {
public static void heapSort(int[] arr) {
int n = arr.length;
// 建堆
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 交换堆顶和末尾元素并调整堆
for (int i = n - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}
public static void heapify(int[] arr, int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
heapify(arr, n, largest);
}
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6, 7};
heapSort(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
3. 复杂度及稳定性:
- 时间复杂度:O(NlogN),建堆O(N) ,调整堆O(logN) ,共N - 1 次调整。
- 空间复杂度:O(1)。
- 稳定性:不稳定,建堆和调整过程中相同值元素位置不可预测。