1. 拉普拉斯算子
在该系列的第八篇文章中,我们曾经介绍过在二维空间拉普拉斯算子的定义为:
这是对函数 的二阶偏导数之和。
2. 拉普拉斯算子的傅里叶变换及其推导
在该系列的第三十二篇文章中,我们曾给介绍过下面的公式
二维连续傅里叶变换:
二维连续傅里叶逆变换:
下面,我们尝试推导一下拉普拉斯算子在频域中的表示。首先考虑傅里叶变换的性质,特别是微分运算的傅里叶变换性质:
一阶微分:在空间域中对 x 方向的微分变换为:
二阶微分:在空间域中对 x 方向的二阶微分变换:
同理,
现在,可以直接将拉普拉斯算子作用在 上的结果进行傅里叶变换:
在频域中,由之前介绍过的公式可知 的傅里叶变换是 ,即
拉普拉斯算子的作用等价于对 乘以一个因子:
这个乘积意味着:频率越高(u 或 v 越大),乘的因子绝对值越大,也就是高频成分被放大。因此频域中的拉普拉斯算子常用于边缘检测、锐化等图像处理任务。
3. 使用 OpenCV C++ 实现频域的拉普拉斯算子
下面的例子,实现频域拉普拉斯算子,并且对原图进行锐化。
在频域中,锐化操作相当于将原图频谱与拉普拉斯响应叠加。具体公式为:
其中 k 是一个控制锐化强度的正数。从空间域视角,这等价于:
#include <opencv2/opencv.hpp>
#include <iostream>
usingnamespace cv;
usingnamespacestd;
// 创建频域拉普拉斯滤波器
Mat createLaplacianFilter(Size size) {
Mat laplacianFilter = Mat::zeros(size, CV_32FC2);
int center_row = laplacianFilter.rows / 2;
int center_col = laplacianFilter.cols / 2;
float factor = (2 * CV_PI) * (2 * CV_PI); // 计算 (2*PI)^2
for (int i = 0; i < laplacianFilter.rows; i++) {
for (int j = 0; j < laplacianFilter.cols; j++) {
float u = (float)(i - center_row);
float v = (float)(j - center_col);
float d_squared = u * u + v * v;
laplacianFilter.at<Vec2f>(i, j)[0] = -factor * d_squared; // −(2π)^2(u^2+v^2)
laplacianFilter.at<Vec2f>(i, j)[1] = 0;
}
}
return laplacianFilter;
}
// 对单个通道应用频域拉普拉斯锐化并返回处理后频域图像的幅度谱
Mat processChannelAndGetProcessedMag(const Mat& src, Mat& dst, double alpha) {
int m = getOptimalDFTSize(src.rows);
int n = getOptimalDFTSize(src.cols);
Mat padded;
copyMakeBorder(src, padded, 0, m - src.rows, 0, n - src.cols, BORDER_CONSTANT, Scalar::all(0));
// 创建频域图像容器 (复数)
Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
Mat complexImg;
merge(planes, 2, complexImg);
// 进行傅里叶变换 (DFT)
dft(complexImg, complexImg);
// 创建拉普拉斯滤波器
Mat laplacianFilter = createLaplacianFilter(complexImg.size());
// 应用拉普拉斯滤波器
Mat resultFreq;
mulSpectrums(complexImg, laplacianFilter, resultFreq, 0);
// 计算处理后频域图像的幅度谱 (用于可视化)
Mat magProcessed;
Mat processedPlanes[2];
split(resultFreq, processedPlanes);
magnitude(processedPlanes[0], processedPlanes[1], magProcessed);
magProcessed += Scalar::all(1); // 避免 log(0)
log(magProcessed, magProcessed);
normalize(magProcessed, magProcessed, 0, 1, NORM_MINMAX);
int cx_processed = magProcessed.cols / 2;
int cy_processed = magProcessed.rows / 2;
Mat q0_processed(magProcessed, Rect(0, 0, cx_processed, cy_processed));
Mat q1_processed(magProcessed, Rect(cx_processed, 0, cx_processed, cy_processed));
Mat q2_processed(magProcessed, Rect(0, cy_processed, cx_processed, cy_processed));
Mat q3_processed(magProcessed, Rect(cx_processed, cy_processed, cx_processed, cy_processed));
Mat tmp_processed;
q0_processed.copyTo(tmp_processed);
q3_processed.copyTo(q0_processed);
tmp_processed.copyTo(q3_processed);
q1_processed.copyTo(tmp_processed);
q2_processed.copyTo(q1_processed);
tmp_processed.copyTo(q2_processed);
// 进行傅里叶逆变换
Mat resultImg;
idft(resultFreq, resultImg, DFT_REAL_OUTPUT);
// 裁剪回原始图像大小
resultImg = resultImg(Rect(0, 0, src.cols, src.rows));
// 归一化到 0-255 并转换为 CV_8U
Mat resultImg_normalized;
normalize(resultImg, resultImg_normalized, 0, 255, NORM_MINMAX, CV_8U);
// 锐化
addWeighted(src, alpha, resultImg_normalized, (1 - alpha), 0, dst);
return magProcessed;
}
int main() {
Mat src = imread(".../girl.jpg");
if (src.empty()) {
cout << "无法加载图像" << endl;
return-1;
}
// 通道分离
vector<Mat> channels;
split(src, channels);
// 对每个通道应用频域拉普拉斯锐化并获取处理后频域图像的幅度谱
double alpha = 1.5; // 锐化强度因子
Mat sharpenedB, sharpenedG, sharpenedR;
Mat processedMagB = processChannelAndGetProcessedMag(channels[0], sharpenedB, alpha);
Mat processedMagG = processChannelAndGetProcessedMag(channels[1], sharpenedG, alpha);
Mat processedMagR = processChannelAndGetProcessedMag(channels[2], sharpenedR, alpha);
// 合并锐化后的通道
vector<Mat> sharpenedChannels = {sharpenedB, sharpenedG, sharpenedR};
Mat sharpenedImg;
merge(sharpenedChannels, sharpenedImg);
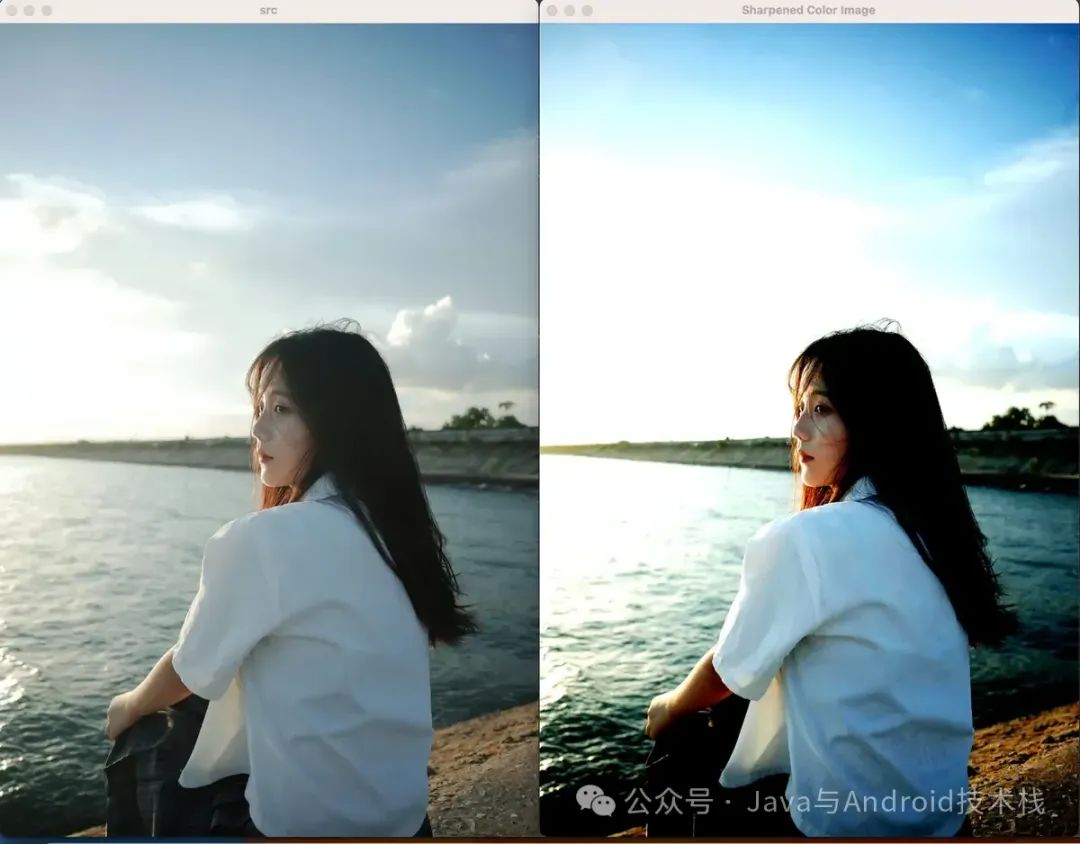
imshow("src", src);
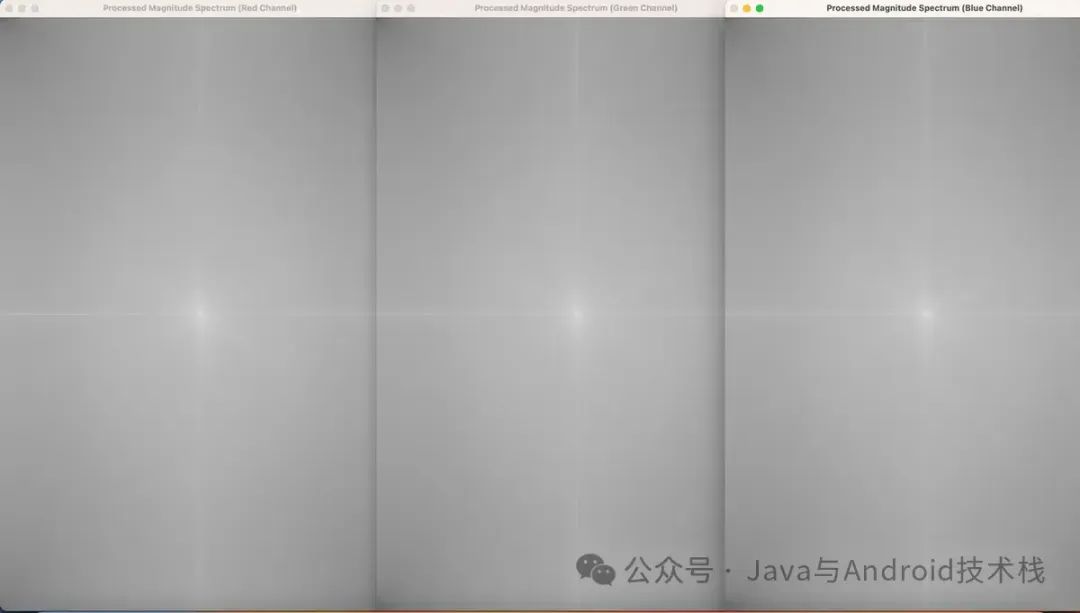
imshow("Processed Magnitude Spectrum (Blue Channel)", processedMagB);
imshow("Processed Magnitude Spectrum (Green Channel)", processedMagG);
imshow("Processed Magnitude Spectrum (Red Channel)", processedMagR);
imshow("Sharpened Color Image", sharpenedImg);
waitKey(0);
return0;
}
频域拉普拉斯响应(即拉普拉斯滤波器作用后的图像)
频域拉普拉斯响应通常不适合直接显示:
1. 拉普拉斯响应具有正负值对称性(不是图像强度)
拉普拉斯是一种二阶微分算子,其结果表示图像的边缘变化强度和方向(凸或凹)。
拉普拉斯响应值可能是正的或负的,而标准图像通道(如
CV_8U)不能表达负值。直接显示会丢失符号信息:正负边缘变得无法分辨。
2. 值域动态范围极大,不适合线性可视化
频域中经过拉普拉斯滤波后,结果的值可能在很大的范围内波动(甚至数万级别),远远超出 [0, 255]。直接转换为 8 位图像会导致:
要么强烈压缩 → 对比度丧失(画面几乎全灰或全白)
要么饱和溢出 → 出现大片“过曝”或“过暗”现象
3. 响应是中间量,本身不代表直观图像内容。
所以,例子中展示了幅度谱,它是对频域响应的一种可视化方式。
4. 总结
在频域中,拉普拉斯算子通过傅里叶变换将空间域的微分操作转换为频域的乘法操作。主要用于增强图像高频成分以突出边缘和细节,典型应用包括图像锐化(通过逆变换叠加原图与拉普拉斯响应)、边缘检测(抑制低频保留高频突变信号)、频域滤波器设计(结合高低通滤波实现带通或带阻效果)以及图像恢复中的正则化约束(抑制噪声)。它是图像增强与分析的非常有用的工具。