C++寻位映射的究极密码：哈希扩展

发布于：2025-05-27 ⋅ 阅读:(167) ⋅ 点赞:(0)

文章目录

位图和布隆过滤器是基于哈希的一种常见应用，通常用来处理大体量数据，提升查找数据的效率

1.位图

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中?

放在哈希表中去寻找？不，这并不现实，因为哈希表的存储也是需要空间消耗的，况且是 40 亿个数据，如此庞大的数据计算机一般是很难存储

因此就诞生了位图的概念，位图简单来说就是把每个数按照哈希函数的计算，存储到每个比特位上。数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为 1，代表存在，为 0 代表不存在

在这里插入图片描述

1.1 位图的结构

template<size_t N>
class bitset
{
public:
	bitset()
	{
		_a.resize(N / 32 + 1);
	}
private:
	vector<int> _a;
};

开辟一个 vector 数组 _a，这里我们以 int 作为位图的基本单位，那么就是把每个数据存储到 int 的比特位上

🔥值得注意的是： resize 的时候无论如何都要加 1，比如 100 个数据，除以 32，等于 3，余 4，那么就需要多一个 int 空间来存储，不能说每次都卡好刚好 32 整除

1.2 位图映射的比特位标记成1

// x映射的那个标记成1
void set(size_t x)
{
	size_t i = x / 32;
	size_t j = x % 32;

	_a[i] |= (1 << j);
}

i 用于确定在第几个 int 里，j 用于确定在第几个 int 的第几位上

在这里插入图片描述

二进制位从右到左是最低位到最高位，所以左移即可

1.3 位图映射的比特位标记成0

// x映射的那个标记成0
void reset(size_t x)
{
	size_t i = x / 32;
	size_t j = x % 32;

	_a[i] &= (~(1 << j));
}

同理，因为按位与是有 0 就是 0，直接计算即可

在这里插入图片描述

1.4 位图映射判断为1 or 0

bool test(size_t x)
{
	size_t i = x / 32;
	size_t j = x % 32;

	return _a[i] & (1 << j);
}

注意这里是 &，而不是 &=，因为只需要判断，而不是修改

位图通常不支持删除功能，因为没有必要删除

2.布隆过滤器

在这里插入图片描述

我们在存储字符串数据时，是通过计算这个字符串的ASC||码值之和，然后通过哈希函数计算存入的，但是这可能会产生哈希冲突，但是数据量太大了，无法通过常规的方法解决

那么最简单的方法就是降低误判率，通过多个不同哈希函数计算，将一个值映射多个位置，这样不至于每次查找都会产生冲突

  1. 用哈希表存储用户记录，缺点：浪费空间
  2. 用位图存储用户记录，缺点：位图一般只能处理整形，如果内容编号是字符串，就无法处理了
  3. 将哈希与位图结合，即布隆过滤器

在这里插入图片描述

再举个现实点的例子，就能理解布隆过滤器存在的必要：

在这里插入图片描述

比如我们在注册账号昵称时，会显示是否已经被取过，先在布隆过滤器中进行查找，若不在，那么成功注册；如果在，那么就到数据库中查询，这样能减少数据库查询次数，降低负载压力，提升整体查询效率

2.1 布隆过滤器的结构

template<size_t N,
    class K = string,
    class Hash1 = BKDRHash,
    class Hash2 = APHash,
    class Hash3 = DJBHash>
class BloomFilter
{
private:
    bitset<N> _bs;
};

Hash1、Hash2、Hash3 是用于计算 string 存储的哈希函数，stl 库里是有 bitset 使用的，直接开辟位图空间即可

传送门：字符串Hash函数对比

2.2 布隆过滤器的哈希函数

struct BKDRHash
{
    size_t operator()(const string& str)
    {
        size_t hash = 0;
        for (auto ch : str)
        {
            hash = hash * 131 + ch;
        }

        //cout <<"BKDRHash:" << hash << endl;
        return hash;
    }
};

struct APHash
{
    size_t operator()(const string& str)
    {
        size_t hash = 0;
        for (size_t i = 0; i < str.size(); i++)
        {
            size_t ch = str[i];
            if ((i & 1) == 0)
            {
                hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
            }
            else
            {
                hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
            }
        }

        //cout << "APHash:" << hash << endl;
        return hash;
    }
};

struct DJBHash
{
    size_t operator()(const string& str)
    {
        size_t hash = 5381;
        for (auto ch : str)
        {
            hash += (hash << 5) + ch;
        }

        //cout << "DJBHash:" << hash << endl;
        return hash;
    }
};

选取了三种计算冲突较小的哈希函数算法进行计算，因为需要多处使用，以仿函数的形式更加方便快捷

2.3 布隆过滤器的插入

void Set(const K& key)
{
    size_t hash1 = Hash1()(key) % N;
    _bs.set(hash1);

    size_t hash2 = Hash2()(key) % N;
    _bs.set(hash2);

    size_t hash3 = Hash3()(key) % N;
    _bs.set(hash3);

    /* cout << hash1 << endl;
     cout << hash2 << endl;
     cout << hash3 << endl << endl;*/
}

由于是以仿函数的方式进行，Hash1() 是匿名对象，有了对象才能以函数的形式调用参数

2.4 布隆过滤器映射判断为true or false

bool Test(const K& key)
{
    size_t hash1 = Hash1()(key) % N;
    if (_bs.test(hash1) == false)
        return false;

    size_t hash2 = Hash2()(key) % N;
    if (_bs.test(hash2) == false)
        return false;

    size_t hash3 = Hash3()(key) % N;
    if (_bs.test(hash3) == false)
        return false;

    return true;
}

2.5 布隆过滤器的优缺点

🚩优点：

  1. 增加和查询元素的时间复杂度为: O(K), ( K 为哈希函数的个数，一般比较小)，与数据量大小无关
  2. 哈希函数相互之间没有关系，方便硬件并行运算
  3. 布隆过滤器不需要存储元素本身，在某些对保密要求比较严格的场合有很大优势
  4. 在能够承受一定的误判时，布隆过滤器比其他数据结构有这很大的空间优势
  5. 数据量很大时，布隆过滤器可以表示全集，其他数据结构不能
  6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算

🚩缺点：

  1. 有误判率，即存在假阳性(False Position)，即不能准确判断元素是否在集合中(补救方法：再建立一个白名单，存储可能会误判的数据)
  2. 不能获取元素本身
  3. 一般情况下不能从布隆过滤器中删除元素
  4. 如果采用计数方式删除，可能会存在计数回绕问题

3.常见面试题

3.1 哈希切割

3.1.1 问题一

给一个超过 100G 大小的 log file，log 中存着 IP 地址, 设计算法找到出现次数最多的 IP 地址？

🛜解决方法：

对于超过 100G 的日志文件，直接加载到内存是不可行的，既然大的不行，就把文件分割为小文件一个个进行

使用哈希函数计算将 IP 映射到不同的小文件中，确保相同 IP 进入同一个文件，对每个小文件，使用哈希表统计 IP 频率，合并所有小文件的统计结果，就能找出出现次数最多的 IP

3.1.2 问题二

与上题条件相同，如何找到 top K 的 IP ？

🛜解决方法：

既然相同 IP 一定进入同一个小文件，用 map 去统计每个文件中 IP 出现的次数即可

3.2 位图应用

3.2.1 问题一

给定 100 亿个整数，设计算法找到只出现一次的整数？

🛜解决方法：

对于 100 亿个整数（约 40GB 数据），直接加载到内存显然不可行。我们可以使用 位图 和 哈希分治 相结合的方法高效解决这个问题——双位图法

在这里插入图片描述
使用两个位图，每个整数对应两位：

  • 00：整数未出现
  • 01：整数出现 1 次
  • 10：整数出现 2 次及以上

假设计算出第一个数据映射第一个位置，且第一次出现，则上面的位图第一位设置为 0，下面位图的第一位设置为 1。其他情况依次类推

template<size_t N>
class twobitset
{
public:
	void set(size_t x)
	{
		// 00 -> 01
		if (!_bs1.test(x) && !_bs2.test(x))
		{
			_bs2.set(x);
		} // 01 -> 10
		else if (!_bs1.test(x) && _bs2.test(x))
		{
			_bs1.set(x);
			_bs2.reset(x);
		}
		// 本身10代表出现2次及以上，就不变了
	}

	bool is_once(size_t x)
	{
		return !_bs1.test(x) && _bs2.test(x);
	}
private:
	bitset<N> _bs1;
	bitset<N> _bs2;
};

最后遍历位图对每一位进行 is_once 函数的判断，符合一次的存入哈希表即可

3.2.2 问题二

给两个文件，分别有 100 亿个整数，我们只有 1G 内存，如何找到两个文件交集？

🛜解决方法：

还是利用两个位图的方式解决，一个文件映射一个位图，对应的位置 & 按位与一下，两个位置都为 1，则这个位置是交集，注意存储的值应该放在 set 里去重

3.2.3 问题三

1 个文件有 100 亿个 int，1G 内存，设计算法找到出现次数不超过 2 次的所有整数

🛜解决方法：

和问题一的方法是一样的，只不过改一下表示方法而已

  • 00：整数未出现
  • 01：整数出现 1 次
  • 10：整数出现 2 次
  • 11：整数出现 3 次及以上

3.3 布隆过滤器应用

3.3.1 问题一

给两个文件，分别有 100亿个 query，我们只有 1G 内存，如何找到两个文件交集？分别给出精确算法和近似算法

🛜解决方法：

近似算法：

用文件 A 的所有 query 构建布隆过滤器，遍历文件 B 的每个 query，判断是否可能在 A 中，对布隆过滤器返回 “可能存在” 的 query，再在文件 A 中精确验证，但是这种方法并不百分百准确，可能存在误判

精确算法：

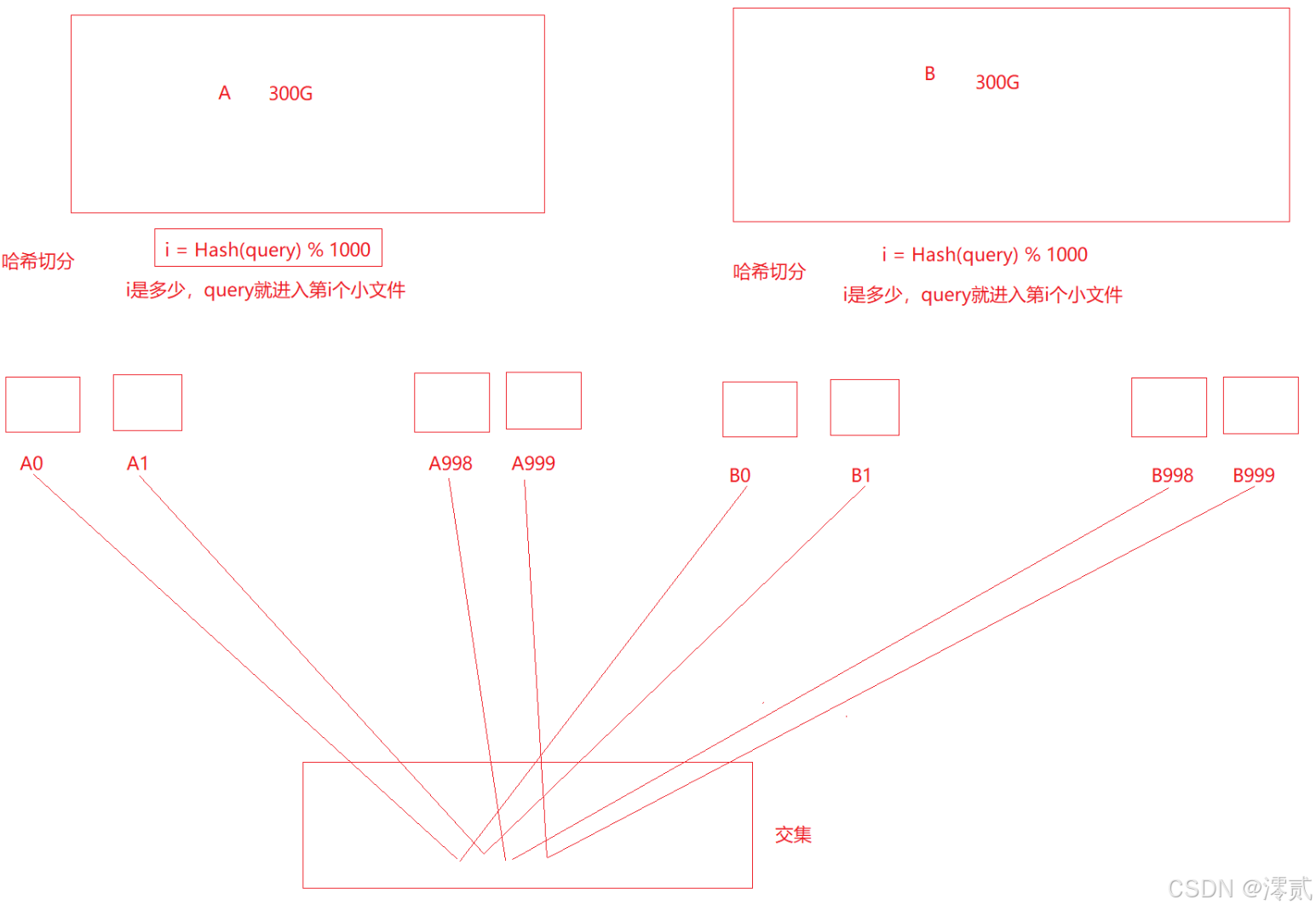
在这里插入图片描述

将 A、B 文件都分割为同样数量的小文件，都上好编号，因为经过相同哈希函数计算，所以 A 和 B 中相同的 query 必定分别进入 Ai 和 Bi 文件中，因此 A0 和 B0 比较，A1 和 B1 进行比较，以此类推即可

在这里插入图片描述

3.3.2 问题二

如何扩展 BloomFilter 使得它支持删除元素的操作?

🛜解决方法：

将标准布隆过滤器的每个二进制位扩展为一个小计数器（通常 4-8 位），当插入元素时增加计数器，删除时减少计数器。只有当计数器为 0 时，才表示该位置未被占用

希望读者们多多三连支持

小编会继续更新

你们的鼓励就是我前进的动力！

请添加图片描述

网站公告

今日签到

点亮在社区的每一天
去签到

热门文章

最新发布