李沐动手深度学习（pycharm中运行笔记）——10.多层感知机+从零实现+简介实现-EW帮帮网

10.多层感知机+从零实现+简介实现（与课程对应）

一、感知机

1、感知机输入输出原理：

输入：给定输入 x（向量）、权重 w（向量）以及偏移b（标量）。
计算过程：感知机的输出是权重 w 和输入 x 做累积，再加上偏移b，然后在结果上做 Sigma 函数。
输出类型：Sigma 函数有多种选择，感知机本质是二分类问题，输出可设置为大于 0 输出 1、小于等于 0 输出 0；也可设置为正 1 和 -1 等不同的二分类形式。

Softmax 对比：Softmax 针对多分类问题，输出 n 个元素；而感知机最多做二分类，输出一个元素。
模型定义：感知机是最早的 AI 模型之一，输出为 1 或 0，或 1 或 - 1。

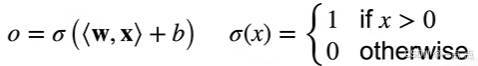
2、训练感知机

感知机训练算法：
- 初始设置：初始时权重 w 设为 0，偏差 b也设为 0 。
- 样本遍历：对样本从 0 开始依次遍历，针对第 i 个样本，计算 yi（标号，取值正 1 或 - 1 ）乘以 w 与 xi 的内积再加上 b。
- 更新条件：若计算结果小于等于 0，表示分类错误，此时对 w 和偏差进行更新，w = w + yi * xi ，b = b + yi ，直到所有类都分类正确。
- 与梯度下降关系：该算法等价于使用批量大小为一的梯度下降，其损失函数包含标号 y 乘以 w 和 x 的内积取负号、与0取 MAX ，与0取MAX 用于根据分类是否正确决定是否更新。

3、收敛定理

假设条件：数据在半径为 r 的区域内，存在一个分界面，其权重的 l2 范数加起来小于等于 1 ，且存在余量 ρ（ρ > 0）使分界面能正确分类所有数据。
收敛情况：在上述条件下，感知机能找到最优解，且在（r² + 1）/ ρ² 次迭代后收敛，数据区域 r 越大收敛越慢，余量 ρ 越大收敛越快。

4、XOR函数

感知机存在的问题：
- XOR 函数拟合失败：感知机作为线性模型，对于 XOR 函数（输入 x 和 y 相同时输出正一类，不同时输出负一类），其二维输入的分隔面为一条直线，无法正确分类所有数据。
- 导致 AI 寒冬：1969 年 Minsky 指出感知机不能拟合 XOR 函数，这直接导致了 AI 的第一个寒冬，许多人因此转行，直到 10—15 年后才有解决办法。

5、总结

感知机是一个二分类模型，是最早的AI模型之一
它的求解算法等价于使用批量大小为1的梯度下降
它不能拟合XOR函数，导致的第一次AI寒冬

二、多层感知机

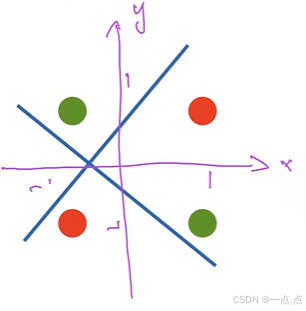
对于四个点的完全分类，单线性模型无法完成。多层感知机是深度学习中经常使用的模型

1、多层感知机的构建步骤

多层感知机的原理：先学习多个简单函数，再将这些简单函数组合起来，从一层变为多层实现复杂分类。
蓝色分隔面：以 x 值为依据，当 x 为 1 时放一边，x 小于 0 时放另一边，对应给一和 4、一和 3 正号，2 和 4 负号。
黄色分隔面：依据 y 的值，给一和 2 正号，3 和 4 负号。
灰色分类器：对蓝色和黄色分类器的结果做处理，相同结果为正，不同结果为负，从而实现正确分类。

2、单隐藏层-单分类

隐藏层大小作为超参数的原因：
- 输入大小固定：数据本身的维度决定了输入大小不可改变。
- 输出大小由类别确定：输出大小取决于分类的类别数量，由数据决定。
- 隐藏层大小可设置：在输入和输出大小都由数据确定的情况下，唯一可设置的超参数就是隐藏层大小。
单隐藏层单分类模型计算过程：
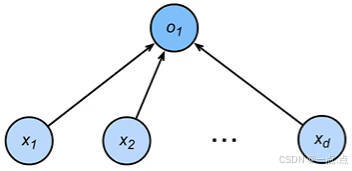
- 模型输入：输入是一个 n 维向量，用于单分类问题。
- 隐藏层计算：隐藏层大小设为 m，有一个 m×n 的权重矩阵 W1 和一个长度为 m 的偏移向量，输入乘以权重加上偏移后经过激活函数（用 Sigma 表示）得到长度为 m 的向量 h 。
- 输出层计算：输出层权重是一个长度为 m 的向量 W2，h 与 W2 转置做累乘再加上标量偏移 B2，最终输出一个标量 o 。

激活函数需为非线性的原因：
- 线性激活函数的结果：假设激活函数 Sigma (x)=x，将导致隐藏层输出 h 等于输入，代入输出层计算后，输出仍是线性函数，模型等价于单层感知机。
- 强调激活函数性质：激活函数不能为线性函数，否则即便叠加多个全连接层，最终也只是简单的线性模型，这是实现中常犯错误。

3、单隐藏层-多分类

多类分类与 Softmax：
- 多类分类本质 ：与多类 Softmax 回归无本质区别，假设做 k 类分类，输出 k 个元素，经 Softmax 操作将输入拉到 0 到 1 区间且和为 1 变成概率。
- 结构变化 ：相比简单 Softmax 回归，加入一层隐藏层就变为多层感知机，输出层 W2 为 m 乘 k 矩阵，偏移 BIAS 为长度为 k 的向量，output 要做一次 Softmax。

4、多隐藏层

多层感知机结构：
- 多层隐藏层：可设置多个隐藏层，如 15 层，包含第一个、第二个、第三个隐藏层等，最终连接到输出层。
- 参数与运算：每个隐藏层都有自己的权重 W 和偏移 b，输入与权重做乘法加上偏移后经过激活函数得到该隐藏层输出，此输出作为下一层输入重复运算，最后输出层不需要激活函数。
超参数选择：
- 隐藏层数量：需选择设置多少个隐藏层，不同数量对模型复杂度有影响。
- 隐藏层大小：每个隐藏层的大小需配置，一般根据输入复杂度决定，若数据复杂，可选择单隐藏层但设置较大规模，也可用多隐藏层且各层规模递减，也可最下层适当扩大再缩小，但不宜先过度压缩再扩张。
激活函数：
- 常用函数：多层感知机常用激活函数有 sigmoid、Tanh 和 Relu，因 Relu 简单，使用较多。
- 多分类函数：做多分类问题时使用 Softmax。

5、总结

多层感知机使用隐藏层和激活函数来得到非线性模型
常用激活函数是Sigmoid、Tanh、ReLU
使用Softmax来处理多类分类
超参数为隐藏层数，和各个隐藏层大小

三、从零实现

1、加载Fashion-MNIST图像分类数据集；返回训练集、测试集的数据迭代器

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2、实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元；初始化模型参数

num_inputs, num_outputs, num_hiddens = 784, 10, 256  # 输入、输出是固定的（数据决定的，是改变不了的）；num_hiddens是自己设定的（超参数）
W1 = nn.Parameter(
    torch.randn(num_inputs, num_hiddens, requires_grad=True)
)
b1 = nn.Parameter(
    torch.zeros(num_hiddens, requires_grad=True) * 0.01
)
W2 = nn.Parameter(
    torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01
)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]

3、激活函数：实现ReLU激活函数

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)  # 就是返回X与0之间的最大值

4、模型；X 是 256x784，所以此处不用转置

def net(X):
    X = X.reshape(-1, num_inputs)  # 先拉成一个2维的矩阵，-1其实就是batch_size
    H = relu(X @ W1 + b1)  # 第一层；这里@代表矩阵乘法
    return (H @ W2 + b2)  # 第二层

5、损失函数

loss = nn.CrossEntropyLoss(reduction='none')

6、训练

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)  # 优化器
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
d2l.plt.show()

7、评估

d2l.predict_ch3(net, test_iter)
d2l.plt.show()

8、完整代码

import torch
from torch import nn
from d2l import torch as d2l


# 多层感知机从零开始实现
# 1、加载Fashion-MNIST图像分类数据集；返回训练集、测试集的数据迭代器
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 2、实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元；初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256  # 输入、输出是固定的（数据决定的，是改变不了的）；num_hiddens是自己设定的（超参数）
W1 = nn.Parameter(
    torch.randn(num_inputs, num_hiddens, requires_grad=True)
)
b1 = nn.Parameter(
    torch.zeros(num_hiddens, requires_grad=True) * 0.01
)
W2 = nn.Parameter(
    torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01
)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]

# 3、激活函数：实现ReLU激活函数
def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)  # 就是返回X与0之间的最大值

# 4、模型；X 是 256x784，所以此处不用转置
def net(X):
    X = X.reshape(-1, num_inputs)  # 先拉成一个2维的矩阵，-1其实就是batch_size
    H = relu(X @ W1 + b1)  # 第一层；这里@代表矩阵乘法
    return (H @ W2 + b2)  # 第二层

# 5、损失函数
loss = nn.CrossEntropyLoss(reduction='none')

# 6、训练
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)  # 优化器
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
d2l.plt.show()

# 7、评估
d2l.predict_ch3(net, test_iter)
d2l.plt.show()

四、简洁实现

1、模型

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10))

2、初始化模型参数

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

3、超参数

batch_size, lr, num_epochs = 256, 0.1, 10

4、损失函数

loss = nn.CrossEntropyLoss(reduction='none')

5、优化器

trainer = torch.optim.SGD(net.parameters(), lr=lr)

6、训练集、测试集数据迭代器

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

7、训练

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.plt.show()

8、完整代码

import torch
from torch import nn
from d2l import torch as d2l


# 多层感知机的简洁实现：通过高级API更简洁地实现多层感知机
# 1、模型
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10))

# 2、初始化模型参数
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

# 3、超参数
batch_size, lr, num_epochs = 256, 0.1, 10

# 4、损失函数
loss = nn.CrossEntropyLoss(reduction='none')

# 5、优化器
trainer = torch.optim.SGD(net.parameters(), lr=lr)

# 6、训练集、测试集数据迭代器
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 7、训练
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.plt.show()

如果此文章对您有所帮助，那就请点个赞吧，收藏+关注那就更棒啦，十分感谢！！！

李沐动手深度学习（pycharm中运行笔记）——10.多层感知机+从零实现+简介实现

一、感知机

1、感知机输入输出原理：

3、收敛定理

4、XOR函数

5、总结

二、多层感知机

1、多层感知机的构建步骤

2、单隐藏层-单分类

4、多隐藏层

5、总结

三、从零实现

四、简洁实现

网站公告

今日签到

热门文章

最新发布