目录
1.算法运行效果图预览
(完整程序运行后无水印)
MATLAB训练结果
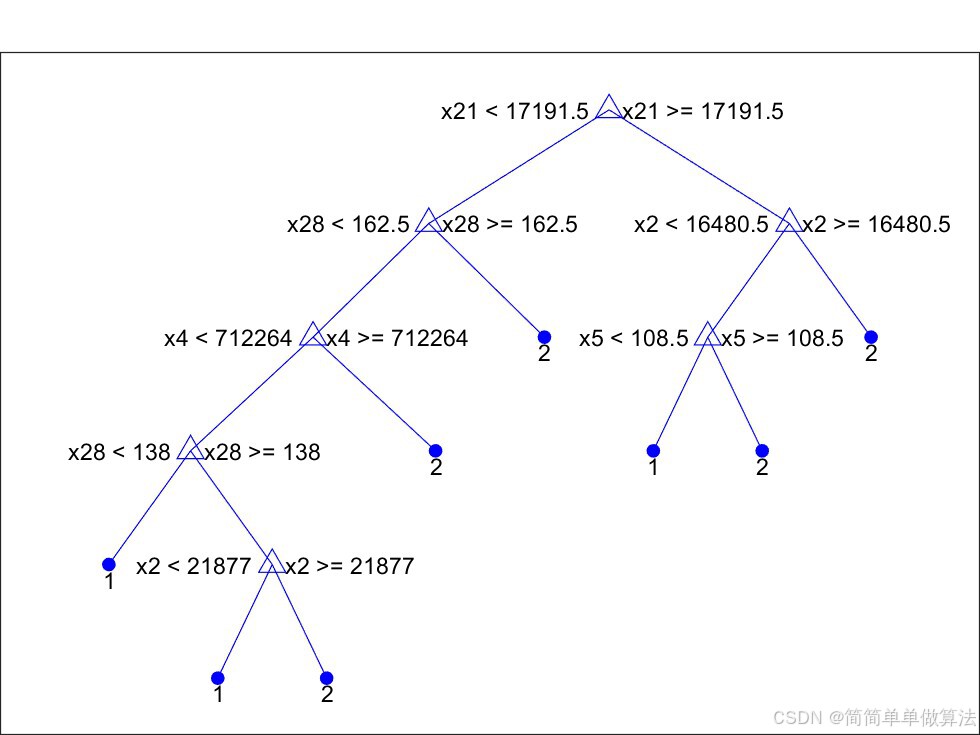
上述决策树判决条件:
分类的决策树
1 if x21<17191.5 then node 2 elseif x21>=17191.5 then node 3 else 1
2 if x28<162.5 then node 4 elseif x28>=162.5 then node 5 else 1
3 if x2<16480.5 then node 6 elseif x2>=16480.5 then node 7 else 2
4 if x4<712264 then node 8 elseif x4>=712264 then node 9 else 1
5 if x22<25170.5 then node 10 elseif x22>=25170.5 then node 11 else 2
6 if x5<108.5 then node 12 elseif x5>=108.5 then node 13 else 1
7 class = 2
8 if x28<138 then node 14 elseif x28>=138 then node 15 else 1
9 class = 2
10 class = 1
11 class = 2
12 class = 1
13 class = 2
14 if x11<658 then node 16 elseif x11>=658 then node 17 else 1
15 if x2<21877 then node 18 elseif x2>=21877 then node 19 else 1
16 if x15<3.5 then node 20 elseif x15>=3.5 then node 21 else 1
17 class = 1
18 if x19<12.5 then node 22 elseif x19>=12.5 then node 23 else 1
19 class = 2
20 class = 1
21 if x22<34117.5 then node 24 elseif x22>=34117.5 then node 25 else 1
22 class = 2
23 class = 1
24 class = 1
25 if x22<34332 then node 26 elseif x22>=34332 then node 27 else 1
26 class = 2
27 class = 1FPGA测试结果:
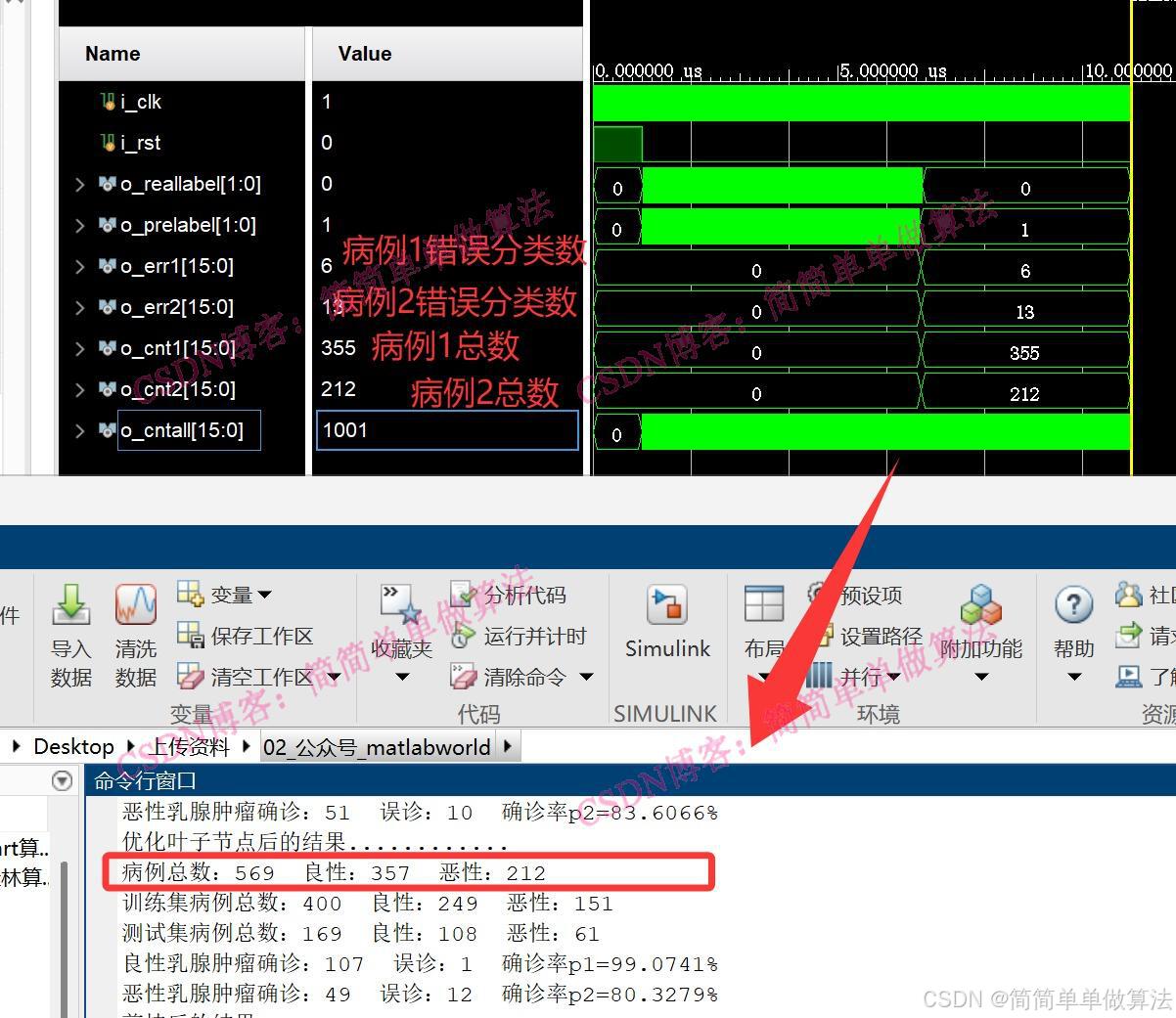
2.算法运行软件版本
matlab2024b
vivado2022.2
3.部分核心程序
(完整版代码包含详细中文注释和操作步骤视频)
...................................................
// 统计分类错误数
if(o_reallabel == 2'd1 & o_prelabel == 2'd2)
r_err1 <= r_err1 + 16'd1;
else
r_err1 <= r_err1;
if(o_reallabel == 2'd2 & o_prelabel == 2'd1)
r_err2 <= r_err2 + 16'd1;
else
r_err2 <= r_err2;
// 保持输出为0(数据收集阶段)
o_err1 <= 16'd0;
o_err2 <= 16'd0;
o_cnt1 <= 16'd0;
o_cnt2 <= 16'd0;
end
// 阶段2:输出统计结果(TEST_NUM+1到TEST_NUM+500个周期)
else if(o_cntall <= TEST_NUM + 500)
begin
o_err1 <= r_err1; // 输出类别1的错误数
o_err2 <= r_err2; // 输出类别2的错误数
o_cnt1 <= r_cnt1; // 输出类别1的样本总数
o_cnt2 <= r_cnt2; // 输出类别2的样本总数
end
// 阶段3:重置计数器(超过TEST_NUM+500后)
else begin
r_err1 <= 16'd0; // 重置中间计数器
r_err2 <= 16'd0;
r_cnt1 <= 16'd0;
r_cnt2 <= 16'd0;
// 保持输出结果不变
o_err1 <= o_err1;
o_err2 <= o_err2;
o_cnt1 <= o_cnt1;
o_cnt2 <= o_cnt2;
end
end
end
// 总计数器和使能信号控制
always @(posedge i_clk or posedge i_rst)
begin
if(i_rst)
begin
o_cntall <= 16'd0; // 复位总计数器
enable <= 1'd0; // 禁用数据生成器
end
else begin
// 循环计数:达到最大值后归零
if(o_cntall == TEST_NUM + 500)
o_cntall <= 16'd0;
else
o_cntall <= o_cntall + 16'd1;
// 在测试阶段(前TEST_NUM个样本)启用数据生成器
if(o_cntall <= TEST_NUM)
enable <= 1'd1;
else
enable <= 1'd0;
end
end
endmodule
05_0137m4.算法理论概述
分类与回归树(Classification and Regression Tree, CART)是一种典型的二叉决策树算法,由Breiman等人于1984年提出。它既可以用于分类问题(输出离散值),也可以用于回归问题(输出连续值)。CART通过递归划分特征空间,构建二叉树结构,其核心思想是基于最小化不纯度(分类)或最小化平方误差(回归)来选择最优分裂特征和阈值,最终形成一棵二叉树。
1.CART算法实现步骤:
输入:训练数据集D,特征集A,停止条件(如最小样本数、最大深度) 输出:CART决策树 1. 若当前节点样本数小于最小样本数或达到最大深度,标记为叶子节点,返回类别/均值。
2. 对每个特征a∈A,遍历所有可能的分裂阈值t,计算分裂后的不纯度(分类)或平方误差(回归)。
3. 选择使不纯度/平方误差最小的特征a和阈值t,生成左右子树。
4. 对左右子树递归调用步骤1-3,直至满足停止条件。
5. 对生成的树进行剪枝处理。
2.特征选择与分裂阈值搜索
对于每个特征a,将样本按特征值排序,遍历所有可能的分裂点(通常取相邻样本的中间值),计算每个分裂点的不纯度或平方误差,选择最优分裂条件。
3.递归分裂与停止条件
递归分裂直至满足以下条件之一:
节点样本数小于预设最小值(如 10)。
所有样本属于同一类别(分类问题)或方差小于阈值(回归问题)。
树的深度达到预设最大值(如 10 层)。
4. 叶子节点赋值
分类树:叶子节点的类别为该节点样本的多数类。
回归树:叶子节点的值为该节点样本的均值。
5.剪枝处理
预剪枝:在分裂时提前限制树的生长,如设置最小样本分裂数、最大深度等。
后剪枝:先生成完整树,再自底向上删除贡献度低的节点。常用方法包括代价复杂度剪枝(Cost-Complexity Pruning),通过最小化损失函数:
Cα(T)=C(T)+α∣T∣
其中,C(T)为训练误差,∣T∣为叶子节点数,α为正则化参数。
CART算法通过递归分裂和剪枝策略,在分类和回归问题中实现了高效的决策建模。MATLAB 训练流程直观易实现,而 FPGA 测试则利用硬件并行性提升预测速度,适用于实时性要求高的场景。
5.算法完整程序工程
OOOOO
OOO
O