【机器学习】支持向量机（SVM）

发布于：2025-06-04 ⋅ 阅读:(26) ⋅ 点赞:(0)

一、支持向量机概述

1.定义

支持向量机是一种基于间隔最大化原则的监督学习模型，它通过找到数据集中的最优超平面来区分不同的类别。在二维空间中，这个超平面可以看作是一条线；在三维空间中，它是一个平面；而在更高维空间中，它是一个超平面。

2.基本原理
  • SVM通过找到数据点之间的最优边界（称为超平面）来区分不同的类别。
  • 这个超平面的选择使得它尽可能地远离每个类别最近的数据点，这些数据点被称为支持向量。
3.关键概念

（1）间隔：数据集所有点到分隔面的最小间隔的2倍，称为分类器或数据集的间隔。SVM的目标是找到一个决策边界，使得数据间隔最大化。

（2）支持向量：

  • 支持向量是那些位于间隔边界上的数据点，它们直接影响超平面的位置和方向。如果移除了这些点，超平面的位置将会改变。

（3）超平面：

  • 在数学上，超平面是一个线性决策边界，可以表示为 w⋅x+b=0，其中 w 是权重向量，x 是特征向量，b 是偏置项。对于二维平面来说，分隔超平面就是一条直线；对于三维及三维以上的数据来说，分隔数据的是个平面，称为超平面，也就是分类的决策边界。
线性可分（一维）

线性不可分（二维及以上）

（4）核函数：

  • 核函数是将原始输入空间映射到新的特征空间的一种函数，使得原本线性不可分的样本在新的特征空间中可能变得线性可分。

（5）软间隔（Soft Margin）：

  •  针对样本不是完全能够划分开的情况，可以允许支持向量机在一些样本上出错，为此要引入“软间隔”的概念。

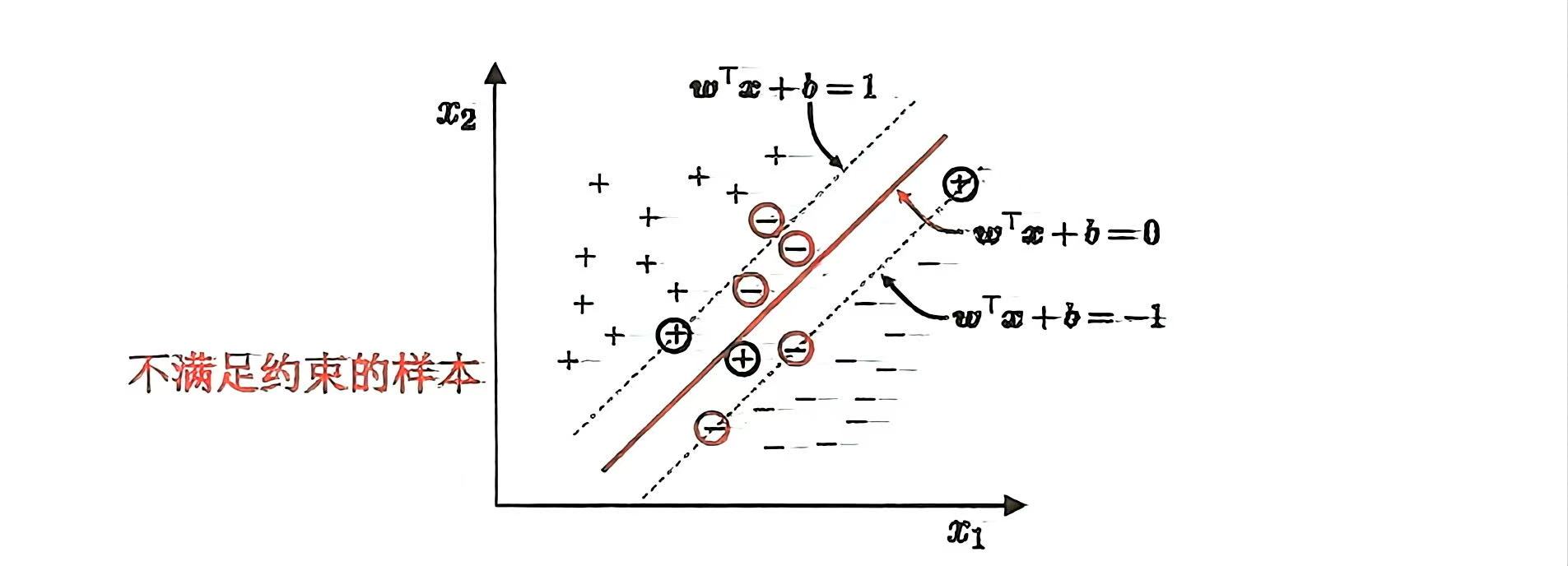
二、求解最大化间隔

如果我们能够确定两个平行超平面，那么两个超平面之间的最大距离就是最大化间隔。

左右两个平行超平面将数据完美的分开，我们只需要计算上述两个平行超平面的距离即可。所以，我们找到最大化间隔：

  • 找到两个平行超平面，可以划分数据集并且两平面之间没有数据点

  • 最大化上述两个超平面

1. 确定两个平行超平面

怎么确定两个平行超平面？我们知道一条直线的数学方程是：y-ax+b=0，而超平面会被定义成类似的形式：

w^{T}x-b=0

推广到n维空间，则超平面方程中的w、x分别为：

如何确保两超平面之间没有数据点？我们的目的是通过两个平行超平面对数据进行分类，那我们可以这样定义两个超平面。

对于每一个向量xi：满足：

wx_{i}+b\geqslant 1   if   y_{i}=+1

或者

wx_{i}+b\leq - 1   if   y_{i}=-1

也就是这张图：所有的红点都是1类，所有的蓝点都是−1类。

整理一下上面的两个超平面：

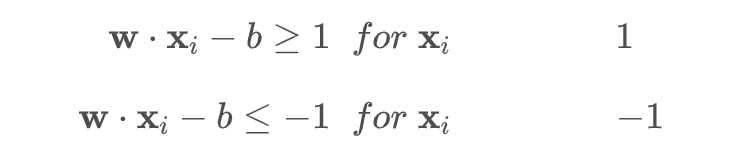
不等式两边同时乘以 yi，-1类的超平面yi=-1，要改变不等式符号，合并后得

y_{i}(wx_{i}+b)-1>=0

2. 确定间隔

如何求两个平行超平面的间隔呢？我们可以先做这样一个假设：

  •  h_{0}是满足约束 wx_{i}-b=1 的超平面

  • h_{1}是满足约束wx_{i}-b=-1 的超平面

  • x_{0}是 h_{0}上的一点

则x_{0} 到平面 h_{1}的垂直距离m 就是我们要的间隔。

这个间隔是可以通过计算出来的，推导还需要一些步骤，直接放结果了就：

m=\frac{2}{||w||}

其中||w||表示w的二范数，求所有元素的平方和，然后在开方。比如，二维平面下：

可以发现，w 的模越小，间隔m 越大。

3. 确定目标

我们的间隔最大化，最后就成了这样一个问题：

显然，为了最大化间隔，仅需要最大化 ||w||^{-1}，这等价于最小化 ||w||^{2}。于是上式可写为：

这就是支持向量机的基本型。

上面的最优超平面问题是一个凸优化问题，可以转换成了拉格朗日的对偶问题，判断是否满足KKT条件，然后求解。我们可以发现，其实最终分类超平面的确定依赖于部分极限位置的样本点，这叫做支持向量。

三、对偶问题

利用拉格朗日优化方法可以把最大间隔问题转换为比较简单的对偶问题，首先定义凸二次规划的拉格朗日函数：

1.引入拉格朗日乘子：

其中

2.对原始变量求偏导并令其为零：

3.代入拉格朗日函数消去 w 和 b：

4.构造对偶问题：

最大化上述拉格朗日函数L(\alpha )，同时满足约束条件：

这是一个不等式约束下的二次函数极值问题，存在唯一解。根据KKT条件，解中将只有一部分（通常是很小的一部分）不为零，这些不为0的解所对应的样本就是支持向量。

四.支持向量机解决数据点分类问题

1.实验要求

实战要求：使用SVM建立自己的垃圾邮件过滤器。首先需要将每个邮件x变成一个n维的特征向量，并训练一个分类器来分类给定的电子邮件x是否属于垃圾邮件 ( y = 1 ) (y=1)(y=1) 或者非垃圾邮件 ( y = 0 ) (y=0)(y=0) 。

数据集：emailSample1.txt, vocab.txt, spamTrain.mat, spamTest.mat

2.具体实现

2.1 词汇表加载

从 vocab.txt 文件中读取词汇表，每行是 编号\t单词 格式，返回一个 dict[word] = index。

def load_vocab(vocab_path='vocab.txt'):
    vocab = {}
    try:
        with open(vocab_path, 'r', encoding='utf-8') as f:
            for line in f:
                idx, word = line.strip().split('\t')
                vocab[word] = int(idx)
    except FileNotFoundError:
        print(f"错误：找不到词汇表文件 {vocab_path}")
    return vocab
2.2 邮件预处理函数

功能：

  • 读取邮件内容并小写化

  • 正则表达式清洗文本：去除HTML、网址、邮箱、数字、$符号等

  • 分词（使用标点符号和空白符切分）

  • 过滤长度 <=1 的 token

  • 把词转换成词汇表中的索引，返回索引列表

def process_email(email_path, vocab):
    try:
        with open(email_path, 'r', encoding='utf-8') as f:
            email = f.read().lower()
    except FileNotFoundError:
        print(f"错误：找不到邮件文件 {email_path}")
        return []

    email = re.sub('<[^<>]+>', ' ', email)
    email = re.sub(r'(http|https)://[^\s]+', 'httpaddr', email)
    email = re.sub(r'[^\s]+@[^\s]+', 'emailaddr', email)
    email = re.sub(r'[0-9]+', 'number', email)
    email = re.sub(r'[$]+', 'dollar', email)

    tokens = re.split(r'[\s{}]+'.format(re.escape(string.punctuation)), email)
    tokens = [t for t in tokens if len(t) > 1]

    word_indices = [vocab[token] for token in tokens if token in vocab]
    return word_indices
2.3词索引转换为特征向量

返回一个 vocab_size 维的 0-1 向量，表示当前邮件中是否包含词汇表中的词。

def email_to_feature_vector(word_indices, vocab_size=1899):
    features = np.zeros(vocab_size)
    for idx in word_indices:
        if 1 <= idx <= vocab_size:
            features[idx - 1] = 1
    return features
2.4 SVM 模型训练

封装 SVM 训练函数：

def train_svm(X, y, kernel='linear', C=1.0, degree=3):
    if kernel == 'linear':
        clf = LinearSVC(C=C, max_iter=5000, random_state=42)
    else:
        clf = SVC(kernel=kernel, C=C, degree=degree, max_iter=5000, random_state=42)
    with warnings.catch_warnings():
        warnings.simplefilter("ignore")
        clf.fit(X, y)
    return clf
2.5 绘制决策边界
  • 使用 PCA 降维后的数据绘制 SVM 的决策边界
  • 绘制 margin 线（±1）和支持向量间隔
  • 可视化红色点（非垃圾邮件）和蓝色点（垃圾邮件）
def plot_decision_boundary(clf, X, y, title):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
                         np.linspace(y_min, y_max, 500))

    if hasattr(clf, "decision_function"):
        Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    else:
        Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
    Z = Z.reshape(xx.shape)

    plt.figure(figsize=(8, 6))
    plt.contour(xx, yy, Z, levels=[-1, 0, 1], linestyles=['--', '-', '--'], colors='k')
    plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='非垃圾邮件', edgecolors='k')
    plt.scatter(X[y == 1, 0], X[y == 1, 1], c='blue', label='垃圾邮件', edgecolors='k')
    plt.title(title)
    plt.xlabel('PCA 特征1')
    plt.ylabel('PCA 特征2')
    plt.legend()
    plt.show()
2.6 主函数 main()

主要流程为：

  1. 加载词汇表和数据文件（.mat）
  2. 提取训练和测试数据
  3. PCA降维用于可视化
  4. 多种核函数下的模型训练和评估
  5. 对示例邮件进行分类测试
def main():
    vocab = load_vocab('vocab.txt')
    if not vocab:
        return

    try:
        train_data = loadmat('spamTrain.mat')
        test_data = loadmat('spamTest.mat')
    except FileNotFoundError:
        print("错误：数据文件不存在。请确认 spamTrain.mat 和 spamTest.mat 在当前目录。")
        return

    X_train = train_data['X']
    y_train = train_data['y'].ravel()
    X_test = test_data['Xtest']
    y_test = test_data['ytest'].ravel()

    # PCA降维到2维，用于可视化
    pca = PCA(n_components=2, random_state=42)
    X_train_pca = pca.fit_transform(X_train)
    X_test_pca = pca.transform(X_test)

    kernels = {
        '线性核': 'linear',
        '多项式核': 'poly',
        '高斯核': 'rbf'
    }

    models = {}

    for name, kernel in kernels.items():
        print(f"\n训练 {name} SVM (C={C})...")
        if kernel == 'poly':
            clf = train_svm(X_train_pca, y_train, kernel=kernel, degree=3, C=C)
        else:
            clf = train_svm(X_train_pca, y_train, kernel=kernel, C=C)
        models[name] = clf

        train_acc = clf.score(X_train_pca, y_train)
        test_acc = clf.score(X_test_pca, y_test)
        print(f"{name} 训练集准确率: {train_acc * 100:.2f}%")
        print(f"{name} 测试集准确率: {test_acc * 100:.2f}%")

        plot_decision_boundary(clf, X_train_pca, y_train, f"{name} SVM 决策边界 (PCA降维)")

    # 示例邮件测试
    word_indices = process_email('emailSample1.txt', vocab)
    if not word_indices:
        print("示例邮件处理失败，退出")
        return
    print("示例邮件词索引（前10个）:", word_indices[:10])

    email_features = email_to_feature_vector(word_indices)
    email_features_pca = pca.transform(email_features.reshape(1, -1))

    print("\n示例邮件预测结果：")
    for name, clf in models.items():
        pred = clf.predict(email_features_pca)[0]
        print(f"{name}: {'垃圾邮件' if pred == 1 else '非垃圾邮件'}")

3.完整代码

import numpy as np
import re
import string
from scipy.io import loadmat
from sklearn.svm import LinearSVC, SVC
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
import warnings

# === 可调参数 ===
C = 10.0  # 修改这里的 C 即可改变模型复杂度

# === 字体设置（支持中文显示）===
font_path = "C:/Windows/Fonts/simhei.ttf"
font_prop = FontProperties(fname=font_path)
plt.rcParams['font.family'] = font_prop.get_name()
plt.rcParams['axes.unicode_minus'] = False


def load_vocab(vocab_path='vocab.txt'):
    vocab = {}
    try:
        with open(vocab_path, 'r', encoding='utf-8') as f:
            for line in f:
                idx, word = line.strip().split('\t')
                vocab[word] = int(idx)
    except FileNotFoundError:
        print(f"错误：找不到词汇表文件 {vocab_path}")
    return vocab


def process_email(email_path, vocab):
    try:
        with open(email_path, 'r', encoding='utf-8') as f:
            email = f.read().lower()
    except FileNotFoundError:
        print(f"错误：找不到邮件文件 {email_path}")
        return []

    email = re.sub('<[^<>]+>', ' ', email)
    email = re.sub(r'(http|https)://[^\s]+', 'httpaddr', email)
    email = re.sub(r'[^\s]+@[^\s]+', 'emailaddr', email)
    email = re.sub(r'[0-9]+', 'number', email)
    email = re.sub(r'[$]+', 'dollar', email)

    tokens = re.split(r'[\s{}]+'.format(re.escape(string.punctuation)), email)
    tokens = [t for t in tokens if len(t) > 1]

    word_indices = [vocab[token] for token in tokens if token in vocab]
    return word_indices


def email_to_feature_vector(word_indices, vocab_size=1899):
    features = np.zeros(vocab_size)
    for idx in word_indices:
        if 1 <= idx <= vocab_size:
            features[idx - 1] = 1
    return features


def train_svm(X, y, kernel='linear', C=1.0, degree=3):
    if kernel == 'linear':
        clf = LinearSVC(C=C, max_iter=5000, random_state=42)
    else:
        clf = SVC(kernel=kernel, C=C, degree=degree, max_iter=5000, random_state=42)
    with warnings.catch_warnings():
        warnings.simplefilter("ignore")
        clf.fit(X, y)
    return clf


def plot_decision_boundary(clf, X, y, title):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
                         np.linspace(y_min, y_max, 500))

    if hasattr(clf, "decision_function"):
        Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    else:
        Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
    Z = Z.reshape(xx.shape)

    plt.figure(figsize=(8, 6))
    plt.contour(xx, yy, Z, levels=[-1, 0, 1], linestyles=['--', '-', '--'], colors='k')
    plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='非垃圾邮件', edgecolors='k')
    plt.scatter(X[y == 1, 0], X[y == 1, 1], c='blue', label='垃圾邮件', edgecolors='k')
    plt.title(title)
    plt.xlabel('PCA 特征1')
    plt.ylabel('PCA 特征2')
    plt.legend()
    plt.show()


def main():
    vocab = load_vocab('vocab.txt')
    if not vocab:
        return

    try:
        train_data = loadmat('spamTrain.mat')
        test_data = loadmat('spamTest.mat')
    except FileNotFoundError:
        print("错误：数据文件不存在。请确认 spamTrain.mat 和 spamTest.mat 在当前目录。")
        return

    X_train = train_data['X']
    y_train = train_data['y'].ravel()
    X_test = test_data['Xtest']
    y_test = test_data['ytest'].ravel()

    # PCA降维到2维，用于可视化
    pca = PCA(n_components=2, random_state=42)
    X_train_pca = pca.fit_transform(X_train)
    X_test_pca = pca.transform(X_test)

    kernels = {
        '线性核': 'linear',
        '多项式核': 'poly',
        '高斯核': 'rbf'
    }

    models = {}

    for name, kernel in kernels.items():
        print(f"\n训练 {name} SVM (C={C})...")
        if kernel == 'poly':
            clf = train_svm(X_train_pca, y_train, kernel=kernel, degree=3, C=C)
        else:
            clf = train_svm(X_train_pca, y_train, kernel=kernel, C=C)
        models[name] = clf

        train_acc = clf.score(X_train_pca, y_train)
        test_acc = clf.score(X_test_pca, y_test)
        print(f"{name} 训练集准确率: {train_acc * 100:.2f}%")
        print(f"{name} 测试集准确率: {test_acc * 100:.2f}%")

        plot_decision_boundary(clf, X_train_pca, y_train, f"{name} SVM 决策边界 (PCA降维)")

    # 示例邮件测试
    word_indices = process_email('emailSample1.txt', vocab)
    if not word_indices:
        print("示例邮件处理失败，退出")
        return
    print("示例邮件词索引（前10个）:", word_indices[:10])

    email_features = email_to_feature_vector(word_indices)
    email_features_pca = pca.transform(email_features.reshape(1, -1))

    print("\n示例邮件预测结果：")
    for name, clf in models.items():
        pred = clf.predict(email_features_pca)[0]
        print(f"{name}: {'垃圾邮件' if pred == 1 else '非垃圾邮件'}")


if __name__ == "__main__":
    main()

4.运行结果

4.1 线性核SVM决策边界(PCA降维)

4.2 多项式核SVM决策边界(PCA降维)

4.3 高斯核SVM决策边界(PCA降维)

4.4 分类结果

4.5 对 C 不同取值的分析

  • 以线性核为例，使用不同的C值进行分析：

  • 在函数中通过定义 C_list = [0.01, 0.1, 1, 10, 100] 进行遍历不同的 C 值。

  • 得到以下的运行结果

  • 分析：当C取值较小值时，可能会出现欠拟合的情形，泛化能力较差；当C取值中等时，拟合良好，泛化能力最佳；当C取较大值时，可能会出现欠拟合的情形，泛化能力较差。

网站公告

今日签到

点亮在社区的每一天
去签到

热门文章

最新发布