一、前言
前面我们已经学习了二叉搜索树和AVL树,它们的查找、插入、删除数据效率都很高,我们首先需要了解它们是怎么操作数据的
首先将所有数据一次性调到内存中,再在内存中进行处理
但问题是内存的容量并不是很大,一般都在GB级别,如果要处理的数据规模非常大,大到内存根本装不下了,那么数据只能先存在硬盘中(硬盘的容量比内存大得多,甚至达到TB级别),处理到某些数据的时候再调到内存中进行处理
为什么不直接从硬盘中处理数据
操作数据需要CPU去执行相关指令,CPU不可以直接和硬盘进行交互,硬盘中的数据必须先调到内存中才能进一步和CPU交互,我们把这个过程称作一次硬盘访问,也可以叫做一次 硬盘IO。由此可以知道访问结点是在硬盘上进行的,节点内的数据操作是在内存中进行的
这样有什么影响呢
硬盘的访问速度是非常慢的,是毫秒级的,内存的单次访问时间是纳秒级的,1毫秒等于100万纳秒(内存的一秒可能就相当于硬盘的一个星期),硬盘的访问时间成本是比较高的,访问的次数肯定是越少越好
比如在下面这样一棵树中找7

具体步骤是
- 在硬盘中找到根结点8,然后将8读到内存里面,再和7进行比较,硬盘访问一次,7比8小,向左子树走
- 在硬盘中找到结点4,将4读到内存里面,和7进行比较,硬盘访问两次,4比7小,向右子树走
- 在硬盘中找到结点6,将6读到内存里面,和7进行比较,硬盘访问三次,6比7小,向右子树走
- 在硬盘中找到结点7,将7读到内存里面,和7进行比较,硬盘访问四次,7等于7,找到了
可以发现,硬盘访问次数和树高正相关,也就是树越高,硬盘的访问次数越多,那么就要想办法降低树高,从而减少硬盘访问次数
为了解决这个问题,B树就出现了
二、B树
示例

上面是一棵B树,可以看出,B树也是一种 平衡搜索树,每个结点不只有一个元素,也不一定有两个分叉,其实是一个多叉平衡搜索树,这样树高就被压缩了
这样不还是要读取那些次数吗
硬盘读取 物理地址连续 的多个字节和读取单个字节耗时几乎没有区别,通俗说就是 硬盘读取包含多个元素的结点和读取只有一个元素的结点耗时几乎一样
上面的 B 树省略了一些信息,其实还包含空结点

把包含数据的结点称为内部结点
下面空结点称为外部结点(失败结点),没有任何信息,只意味着查找失败,所以也叫失败结点
叶子结点:内部节点的最后一层
定义
B 树,也被称为 B- 树,是一种自平衡的多路搜索树,单个结点可以拥有的最多子结点数量,称为 B 树的阶级。B 树可以是空树,若不是空树,一颗 m 阶的 B 树需要满足:
- 多路:
- 根结点:至少有 1 个元素,2 个分支
- 除根节点和叶子节点:每个节点至少有⌈m/2⌉(向上取整)个分支,[m/2]-1 个元素(结点内元素个数比分支数少 1 )
- 平衡:
- 所有叶子节点都在同一层上
- 有序:
- 每个节点中的键(元素)按升序排列,任一元素的左子树都小于它,右子树都大于它
查找数据
B 树的查找和二叉搜索树很像,只不过一个结点中可能有多个元素,总体思路就是:
- 结点内有多个元素,从左到右依次进行比较
- 如果比它小,继续向后比较
如果比它大,走左子树 - 如果比到最后,走最右边的子树
示例:

查找 18 :
- 18与根结点进行对比,18 < 20,查找20的左子树
- 结点中有两个数,顺序查找,18 > 6,继续向后比较,18 > 15,查找15的右子树
- 结点中有两个数,顺序查找,18 > 16,继续向后比较,18 = 18,找到了
找 45 :
- 45 > 20,查找20右子树
- 45 > 28,继续向后查找,45 > 39,向后,45 < 50,查找50的左子树
- 45 < 46,查找46左子树
- 树为空,所以没有该数据
插入数据
总体思想就是先找到插入的位置(一定是叶子节点这一层)进行插入,插入后可能会超出结点的最大元素数量,如果超出最大数量进行调整
将超出结点的最大元素数量称为 上溢出,我们在上面已经了解到,结点中元素个数在 [m/2]-1 到 [m/2] 之间,如果超过了[m/2]就是上溢出
示例:

这是一棵 3 阶B树,如果节点内元素个数大于 2 ,就发生了上溢出
插入20
找插入位置:
- 和根结点比较,20 < 25,查找左子树
- 和12比较,20 > 12,查找右子树
- 和23比较,20 < 23,插入到23左边
插入后

没有出现上溢出(没有超出元素个数的上限),不需要调整
再插入17
找到 17 的插入位置:20 的左侧
插入后

发生上溢出,进行调整
上溢出的调整:
将第[m/2](上取整)个元素作为分割点,分成左右两部分
再将第[m/2]个元素上移到父结点上
我们把调整上溢出的方法称为 分裂

最终结果

叶子结点出现上溢出是需要将元素上移的,那么如果元素上移后父结点也出现了上溢出呢?
父结点出现上溢出示例:
插入36
36应该插入到37左侧
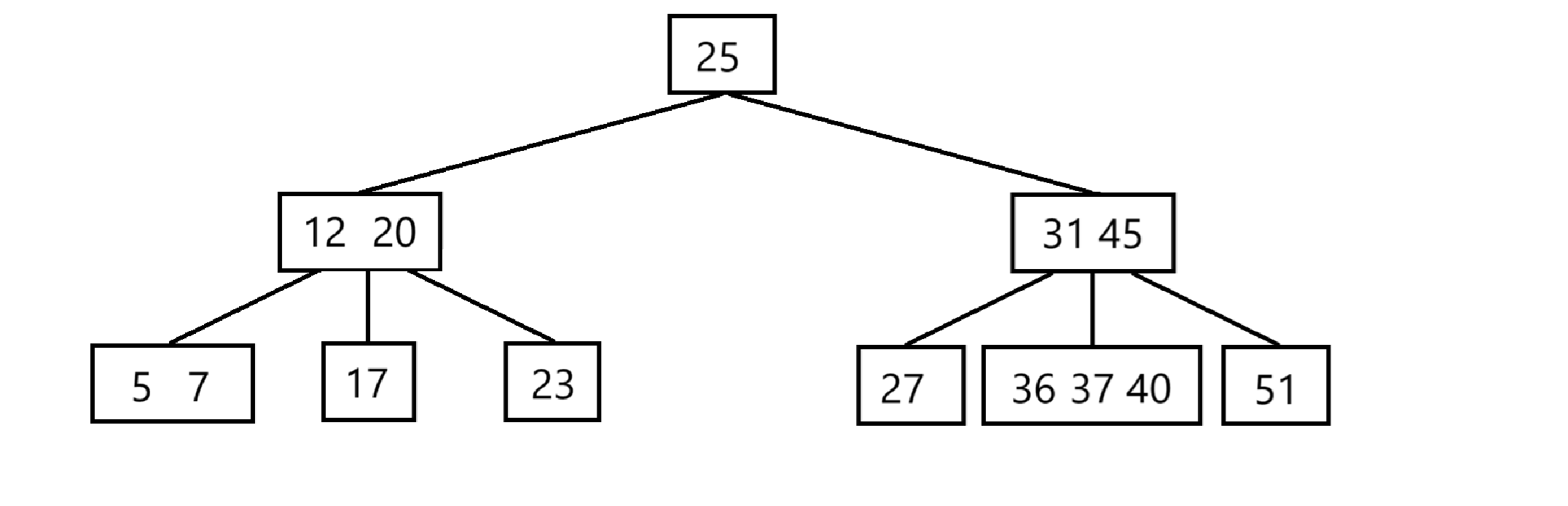
上溢出,以37作为分割点,37上移

此时发现 父结点也上溢出,表明分裂操作可能不只做一次,可能需要一直向上分裂,直到不会出现上溢出
以37作为分割点,将37上移

需要注意,分裂时,如果发生分裂的结点有左子树或右子树,需要连带左子树和右子树一起
现在我们已经知道,插入元素可能会导致父结点上溢出,那如果不断上溢出,元素不断上移,会不会最终导致根结点上溢出呢?
根结点上溢出 示例:
这里我直接将 36 插入根结点了,不严谨,掌握如何处理根结点上溢出的方法就好

将 36 作为分割点,上移,作为新的根结点,其左右分裂

插入数据的代码实现
删除数据
删除 B 树中的元素,和搜索二叉树中删除的结点有左右子树思路相似,插入操作容易导致上溢出,而删除操作因为少了元素,容易导致 下溢出,也就是可能会低于节点元素的下限
总体思路:
- 删除非叶子结点元素最终都转换成删除叶子结点元素
- 删除叶子结点元素
- 没有下溢出无需调整
- 下溢出
- 兄弟够借:借(父下来,兄上去)
- 兄弟不够借:合并(可能导致父结点下溢出)

这是一棵 5 阶B树,结点内元素个数要满足在 2 和 3 之间,如果进行删除操作后结点元素个数少于两个,那就会发生下溢出需要调整
- 删除叶子结点的元素
删除57
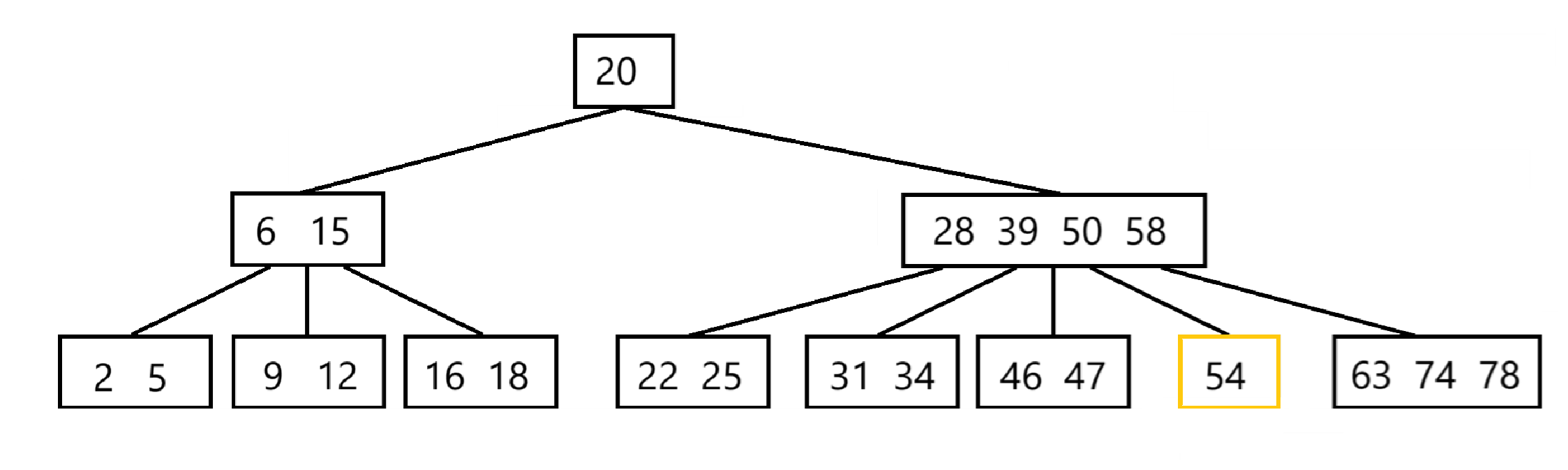
有一个叶子结点中只有一个元素 54,少于 2 个, 发生下溢出
首先考虑 和左右兄弟借一个元素
如果够借,意思是左右兄弟少一个元素后不会下溢出(左右兄弟有一个够借就可以)左右兄弟够借
上图中右兄弟中有三个元素,少一个之后变成两个,不会发生下溢出,所以可以借右兄弟
先将两个节点的父结点下移到左边的节点中,再把右兄弟最左边的元素上移到父节点原来的位置

左右兄弟不够借
删除58,直接删除后变为:
 有一个叶子节点中只有一个元素,发生下溢出,而且左右兄弟都不够借
有一个叶子节点中只有一个元素,发生下溢出,而且左右兄弟都不够借
和其中一个兄弟合并
和左兄弟合并:
父亲元素下移到左边的结点,下溢出的结点合并过来,移除空的子树和父结点

和右兄弟合并:
父亲元素下移到下溢出的结点,右边的结点合并过来,移除空的子树和父亲元素

由此可以总结
不管和左兄弟还是右兄弟合并,都是先将父亲元素下移到左边的结点,
再将右结点合并过来
上面举的例子都很刚刚好,但是如果发生下溢出,我们的方法中有一步是将父结点下移,而父结点中的元素下移了,还需要检查父亲结点有没有下溢出
- 删除非叶子节点中的元素,类似二叉搜索树中删除的结点有左右子树的情况,总体思路就是:
- 用中序前驱或中序后继代替要删除的结点(拿中序后继举例子)
- 删去中序后继结点(最终还是转化为删除叶子结点中的元素)
删除20
20的中序后继元素是22
用后继22替换20,再删除叶子结点上的22

此时结点25只有一个元素,出现了下溢出
进行调整后
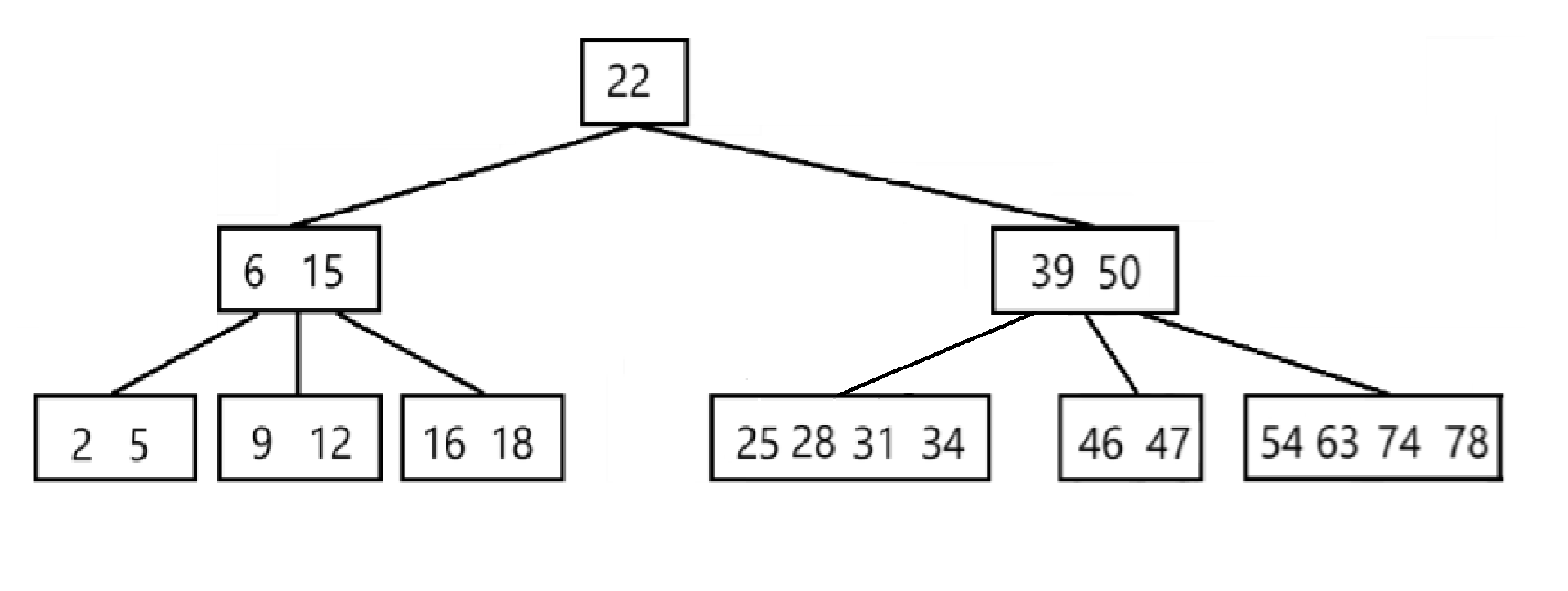
- 如果除叶子结点之外的结点出现了下溢出
删除6
找到6的中序后继元素9,9替换6,删除9

发生了下溢出,进行调整后(和右兄弟合并)

父结点又发生了下溢出
看父结点的左右兄弟够不够借,如果够借直接按照够借的方法(需要注意的是,如果上移的兄弟结点有子树,需要把兄弟结点中最左边的子树挪到发生下溢出的结点)
不够借,上图这种情况
继续执行合并操作
22下移到左边的结点,再将右边的结点并过来
需要注意,右边的结点如果有子树,也要一起并过来
