自动求导与计算图
自动求导 (Autograd)
PyTorch的torch.autograd模块负责自动计算张量的梯度,无需手动推导导数公式。
重点⭐
requires_grad属性:张量(Tensor)的requires_grad属性若为True,PyTorch会跟踪其所有操作,构建计算图。
x = torch.tensor([2.0], requires_grad=True)
- 梯度计算:执行前向计算后,调用
.backward()自动计算梯度,结果存储在叶子节点的.grad属性中。
y = x ** 2 # y = x² y.backward() # 计算梯度 dy/dx = 2x print(x.grad) # 输出 tensor([4.0])
- 梯度清零:训练时需在每次参数更新后手动清零梯度,避免累积:
optimizer.zero_grad() # 清零梯度
- 禁用梯度跟踪:使用
torch.no_grad()上下文管理器可关闭梯度计算,节省内存:
with torch.no_grad(): inference = model(input) # 不记录计算图
- 分离计算:分离计算指的是将某个张量从当前的计算图中“断开”,使其不再参与梯度传播。PyTorch通过
detach()方法实现这一点,生成的新张量与原张量共享数据,但不跟踪梯度,且requires_grad=False。
🖊️作用:
- 阻止梯度传播:避免某部分计算的梯度影响上游参数。
- 节省内存:减少计算图占用的内存。
- 固定特征:例如在迁移学习中冻结预训练模型的参数。
import torch
x = torch.tensor([2.0], requires_grad=True)
y = x ** 2 # y = x²,计算图被跟踪
z = y.detach() # z是从y分离的新张量,不参与梯度计算
# 对z进行后续操作
w = z + 1 # 由于z被分离,w不会追踪到x的梯度
w.backward() # 仅计算w对z的梯度(但z的梯度传播在此终止)
print(x.grad) # 输出:None(因为z是分离的,梯度不会传播到x)
z被分离后,任何基于z的操作(如w = z + 1)不会影响x的梯度。w.backward()只会计算w对z的梯度,但梯度传播到z时被截断,因此x.grad为None。
计算图 (Computational Graph)
计算图是PyTorch动态记录张量操作的数据结构,用于反向传播时的梯度计算;每次前向传播时实时构建计算图,灵活支持可变结构(如循环神经网络)
动态图 vs 静态图
- 动态图(PyTorch):
每次前向传播时实时构建计算图,灵活支持可变结构(如循环神经网络)。 - 静态图(如TensorFlow 1.x):
需预先定义计算图,灵活性较低。
计算图的组成
- 节点(Node):表示张量或操作(如加法、乘法)。
- 边(Edge):表示数据流动(张量的依赖关系)。
示例
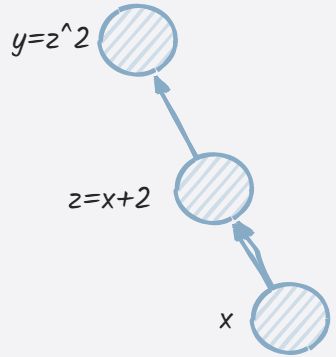
以 y = ( x + 2 ) 2 y=(x+2)^2 y=(x+2)2为例,其中 z = x + 2 , y = z 2 z = x + 2,y=z^2 z=x+2,y=z2
import torch
x = torch.tensor([3.0,4.0], requires_grad=True)
z = x + 2
y = z ** 2
# 反向求导
y.sum().backward()
print("x的值:", x) # tensor([3., 4.], requires_grad=True)
print("y的值:", y) # (x + 2) ^ 2; tensor([25., 36.], grad_fn=<PowBackward0>)
print("dy/dx 的值:", x.grad) # 2(x + 2);tensor([10., 12.])
print("x.gard:", x.grad_fn) # None
print("y.gard:", y.grad_fn) # <PowBackward0 object at 0x000002A20A1FC6A0>
print("z.gard:", z.grad_fn) # <AddBackward0 object at 0x000002A20A1FF8E0>
反向传播与梯度累积
- 链式法则:通过计算图反向遍历,逐层应用链式法则计算梯度。
- 非标量张量:需为
.backward()指定gradient参数作为梯度权重:
import torch
x = torch.tensor([3.0,4.0], requires_grad=True)
y = x * 2
y.backward(torch.tensor([1.0, 0.1]))
print(x.grad) # tensor([2.0000, 0.2000])
- 保留计算图:默认反向传播后计算图会被销毁,设置
retain_graph=True可保留
loss.backward(retain_graph=True) # 保留计算图供后续使用
叶子节点与中间变量
- 叶子节点:用户直接创建的张量(如参数),梯度存储在
.grad中。 - 中间变量:由操作生成的张量,默认不保留梯度(节省内存),可通过
.retain_grad()保留
y = x + 2
y.retain_grad() # 保留y的梯度
z = y ** 2
z.backward()
print(y.grad) # 输出 2y
自定义求导操作 torch.autograd.Function
Variable与Function组成了计算图。
- 而
Variable就相当于计算图中的节点 Function就相当于是计算图中的边,它实现了对一个输入Variable变换为另一个输出的Variable
PyTorch的torch.autograd.Function允许用户自定义前向传播(Forward)和反向传播(Backward)的逻辑,从而实现非标准操作的自动求导或优化梯度计算的性能。这在以下场景中非常有用:
- 实现新的数学操作(如自定义激活函数、特殊损失函数)。
- 优化复杂操作的梯度计算(避免PyTorch自动跟踪的低效性)。
- 融合多个操作(如将多个步骤合并为一个计算单元,减少内存占用)。
核心概念
- 每个
Function子类代表一个可微分的运算 - 必须实现两个静态方法:
forward(): 定义前向计算逻辑backward(): 定义梯度计算逻辑
- 通过
apply()方法调用(如MyFunc.apply(input))
关键步骤:
- 创建子类:继承
torch.autograd.Function。 - 实现
forward方法:定义前向传播的计算。这是实际执行操作的地方。 - 实现 `backward 方法:定义反向传播的梯度计算。这个方法将接收关于输出的梯度,并计算关于输入的梯度。
- 使用:通过调用该子类的
apply方法来使用这个自定义操作。
class MyReLU(torch.autograd.Function):
@staticmethod
def forward(ctx, input):
ctx.save_for_backward(input) # 保存输入供反向传播使用
return input.clamp(min=0) # ReLU: 小于0的值截断为0
@staticmethod
def backward(ctx, grad_output):
input, = ctx.saved_tensors
grad_input = grad_output.clone()
grad_input[input < 0] = 0 # 梯度规则:输入<0的位置梯度为0
return grad_input
x = torch.tensor([-1.0, 2.0], requires_grad=True)
y = MyReLU.apply(x) # 调用自定义Function的apply方法
y.backward(torch.tensor([1.0, 1.0]))
print(x.grad) # 输出:tensor([0.0, 1.0])
完整示例:自定义LeakyReLU
class LeakyReLU(torch.autograd.Function):
@staticmethod
def forward(ctx, x, slope=0.1):
ctx.save_for_backward(x)
ctx.slope = slope # 保存非张量参数
return torch.where(x > 0, x, slope * x)
@staticmethod
def backward(ctx, grad_out):
(x,) = ctx.saved_tensors
slope = ctx.slope
grad_x = grad_out * torch.where(x > 0, 1, slope)
return grad_x, None # 斜率 slope 不需要梯度
# 使用方式
x = torch.randn(5, requires_grad=True)
y = LeakyReLU.apply(x, 0.05)
loss = y.sum()
loss.backward()