目录
1.前言
时间序列预测在能源、气象等领域具有重要应用价值。传统方法如ARIMA、SVM等在处理非线性、非平稳序列时存在局限性,而深度学习模型(如LSTM)虽能捕捉时序特征,但对初始参数敏感,且复杂序列需预处理以提升预测精度。变分模态分解(VMD)可将复杂时序分解为多个平稳模态分量,LSTM可有效建模序列长期依赖关系,粒子群优化(PSO)则用于优化GRU的关键参数,形成 “分解-优化-预测” 的完整框架。
2.算法运行效果图预览
(完整程序运行后无水印)
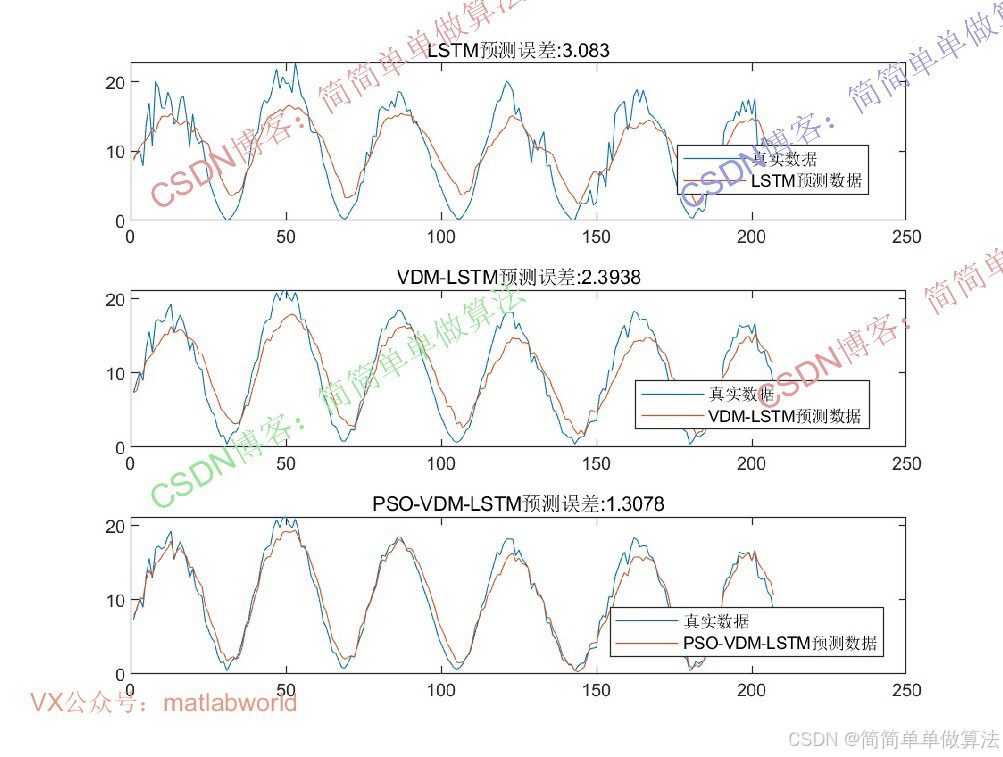

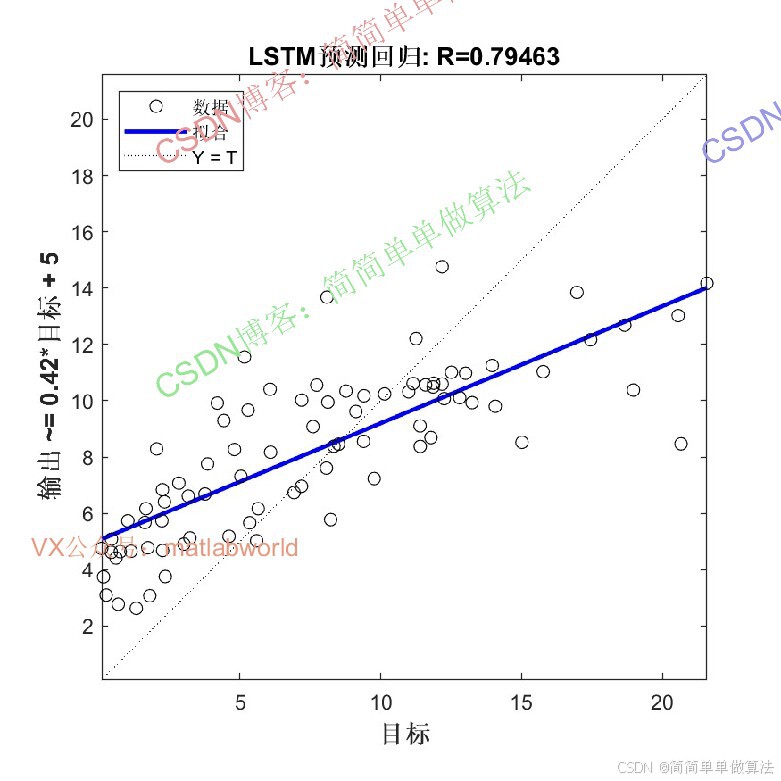
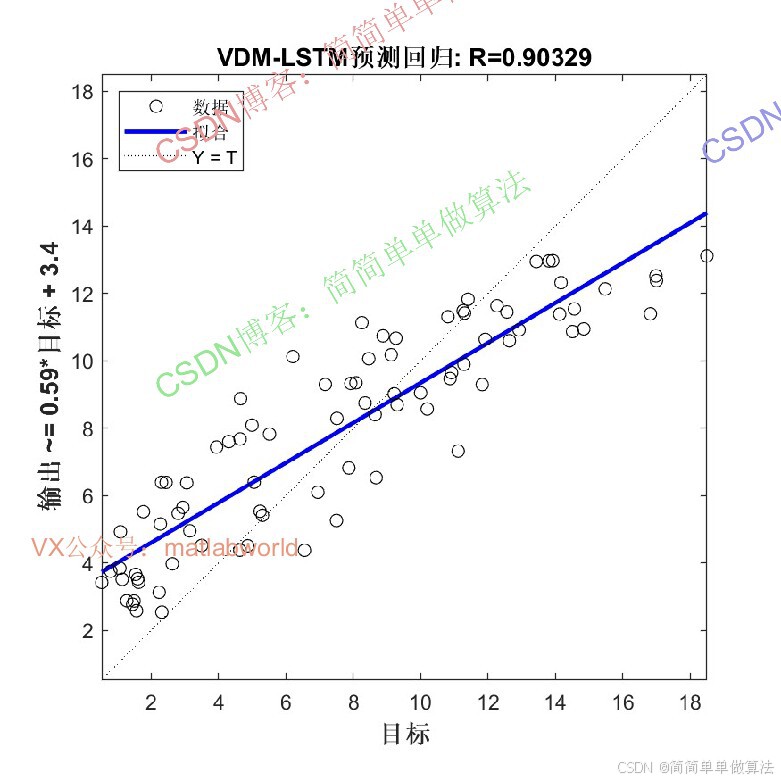
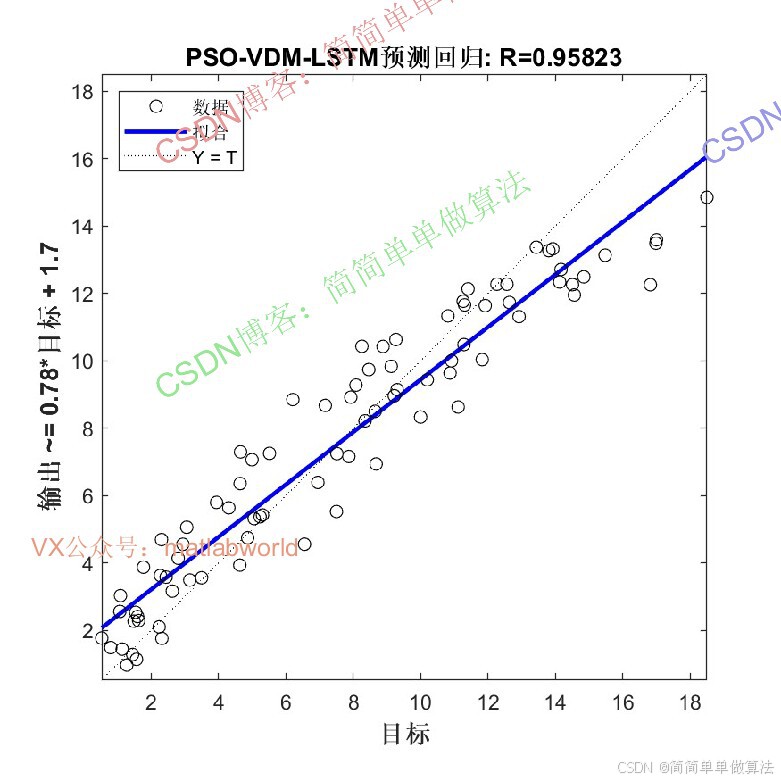
3.算法运行软件版本
Matlab2024b(推荐)或者matlab2022a
4.部分核心程序
(完整版代码包含中文注释和操作步骤视频)
...................................................................
layers = [ ...
sequenceInputLayer(indim)
gruLayer(Nlayer)
lstmLayer
fullyConnectedLayer(outdim)
regressionLayer];
%参数设置
options = trainingOptions('adam', ... % 优化算法Adam
'MaxEpochs', 200, ... % 最大训练次数
'GradientThreshold', 1, ... % 梯度阈值
'InitialLearnRate', LR, ... % 初始学习率
'LearnRateSchedule', 'piecewise', ... % 学习率调整
'LearnRateDropPeriod', 60, ...
'LearnRateDropFactor',0.2, ...
'L2Regularization', 0.01, ... % 正则化参数
'ExecutionEnvironment', 'cpu',... % 训练环境
'Verbose', 0, ... % 关闭优化过程
'Plots', 'training-progress'); % 画出曲线
%训练
[net,INFO] = trainNetwork(Pxtrain, Txtrain, layers, options);
Rerr = INFO.TrainingRMSE;
Rlos = INFO.TrainingLoss;
%预测
Tpre1 = predict(net, Pxtrain);
Tpre2 = predict(net, Pxtest);
%反归一化
TNpre1 = mapminmax('reverse', Tpre1, Norm_O);
TNpre2 = mapminmax('reverse', Tpre2, Norm_O);
%数据格式转换
TNpre1s(d,:) = cell2mat(TNpre1);
TNpre2s(d,:) = cell2mat(TNpre2);
T_trains(d,:) = T_train;
T_tests(d,:) = T_test;
Rerrs(d,:)=Rerr;
Rloss(d,:)=Rlos;
end
2215.算法仿真参数
%pso参数
Npeop = 10; %搜索数量
Iter = 10; %迭代次数
DD = 2; %搜索空间维数
%每个变量的取值范围
tmps(1,:) = [10,100]; %
tmps(2,:) = [0.0001;0.05]; %
%学习因子
c1 = 2;
c2 = 2;
%用线性递减因子粒子群算法
Wmax = 1; %惯性权重最大值
Wmin = 0.8; %惯性权重最小值
%GRU参数
options = trainingOptions('adam', ... % 优化算法Adam
'MaxEpochs', 200, ... % 最大训练次数
'GradientThreshold', 1, ... % 梯度阈值
'InitialLearnRate', LR, ... % 初始学习率
'LearnRateSchedule', 'piecewise', ... % 学习率调整
'LearnRateDropPeriod', 60, ...
'LearnRateDropFactor',0.2, ...
'L2Regularization', 0.01, ... % 正则化参数
'ExecutionEnvironment', 'cpu',... % 训练环境
'Verbose', 0, ... % 关闭优化过程
'Plots', 'training-progress'); % 画出曲线6.算法理论概述
6.1变分模态分解(VMD)
VMD是一种自适应信号分解方法,通过构建变分模型将原始序列分解为若干模态分量(IMF),每个分量对应特定频率尺度,且带宽之和最小化。该过程通过交替迭代更新各模态的频率和幅值实现,无需预设分解层数(实际应用中需结合数据特性确定或优化)。


6.2 LSTM
LSTM是一种特殊的循环神经网络,它通过引入门控机制来控制信息的流动,从而能够有效捕捉时间序列中的长距离依赖关系 。LSTM的核心是记忆单元,它可以存储和更新时间序列中的信息。
6.3 粒子群优化(PSO)
PSO模拟鸟群觅食行为,通过粒子间的信息共享搜索最优解。每个粒子代表一个候选解,通过更新自身速度和位置逼近全局最优。粒子状态由位置Xi和速度Vi表示,需跟踪个体最优位置Pbest,i和全局最优位置Gbest。
适应度函数:
针对VMD-LSTM模型,PSO需优化的参数包括:
LSTM隐藏层节点数nh
学习率η

7.参考文献
[1]彭德烊,赵胜利,吴圆圆,et al.基于VMD和LSTM的全球平均气温预测[J].Climate Change Research Letters, 2024, 13.DOI:10.12677/ccrl.2024.135122.
[2]罗潇远 刘杰 杨斌 覃涛 陈昌盛 杨靖.基于改进鱼鹰优化算法与VMD-LSTM的超短期风电功率预测[J]. 2025.
8.算法完整程序工程
OOOOO
OOO
O