数据结构第八章（六）-置换选择排序和最佳归并树

置换-选择排序和最佳归并树

还记得我们上一篇说的吗？

对 r 个初始归并段，做 k 路归并，则归并树可以用 k 叉树表示， 若树高为 h，则归并趟数 = h-1 = ⌈ logkr ⌉，k 越大，r 越小，归并趟数越少，读写磁盘次数越少。

我们还说了如果能增加初始归并段的长度，则可以减少初始归并段的数量 r 。若一共有 N 个记录，内存工作区可以容纳 L 个记录，则初始归并段数量 r = N/L。

那么这就是我们有“置换-选择排序”的原因了，可以用“置换-选择排序”进一步减少初始归并段的数量。

一、置换-选择排序

我们之前进行初始化的之后，是这样的：

可以看到我们输入缓冲区1、2两个加起来也只能容纳 6 个记录，所以用这种方式构造的初始归并段，里面同样也只能包含 6 个记录。

这太少了，我们怎么解决呢？

既然少那开多点就可以了呗。我们在内存中开辟一片更大的区域，专门用这片区域来进行内部排序，不就可以得到更长的初始归并段了嘛

得到更长的初始归并段之后，我们初始归并段的数量 r 就会下降，这就刚好是我们说的：r 越小，归并趟数越少，读写磁盘次数越少。

我们把图给简化一下，初始待排序关键字就是这样，一共有 24 个元素。我们假设用于内部排序的工作区只能容纳 3 个记录，即：

如果要是之前的初始化方法，我们就会生成 24/3 = 8 个初始归并段。

不多说了，我们来看置换-选择排序方法，这个方法看了就懂了，so easy的。

首先读入三个元素：

我们把最小的元素“置换”出去，即放到初始归并段输出文件的 归并段 1 中

首先在内存工作区中选出最小的，即元素“4”，放到归并段 1 中：

接着我们从初始待排序文件中拿一个补上，即元素“7”：

接着再在内存工作区中选出最小的，即元素“6”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“13”：

再在内存工作区中选出最小的，即元素“7”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“11”：

再在内存工作区中选出最小的，即元素“9”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“16”：

再在内存工作区中选出最小的，即元素“11”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“14”：

再在内存工作区中选出最小的，即元素“13”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“10”：

再在内存工作区中选出最小的，即元素“10”

但是！！！此时我们就会发现，元素“10”如果放到 归并段 1 中，那归并段 1 就不是递增的了，所以这个元素不能放到 归并段 1 中。

故我们把它留在内存工作区中，先不管它：

此时我们在不管元素“10”的情况下，在内存工作区中选出最小的，即元素“14”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“22”：

我们在不管元素“10”的情况下，再在内存工作区中选出最小的，即元素“16”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“30”：

我们在不管元素“10”的情况下，再在内存工作区中选出最小的，即元素“22”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“2”：

我们在不管元素“10”的情况下，再在内存工作区中选出最小的，即元素“2”

但是！！！此时我们又会发现，元素“2”如果放到 归并段 1 中，那归并段 1 就不是递增的了，所以这个元素不能放到 归并段 1 中。

故我们把它留在内存工作区中，也不管它：

此时我们在不管元素“10”、元素“2”的情况下，在内存工作区中选出最小的，即元素“30”，放到归并段 1 中：

我们再从初始待排序文件中拿一个补上，即元素“3”：

我们在不管元素“10”、元素“2”的情况下，再在内存工作区中选出最小的，即元素“3”

但是！！！此时我们又会发现，元素“3”如果放到 归并段 1 中，那归并段 1 就不是递增的了，所以这个元素不能放到 归并段 1 中。

故我们也把它留在内存工作区中，也不管它。

BUT此时我们发现，这个内存工作区一共就这么大，现在里面三个元素我们都不管了，那占着也没法让别的元素过来，所以我们现在的 归并段 1 到此结束，让这三个元素再开一个 归并段 2：

归并段 1 就此落幕：

我们把最小的元素“置换”出去，即放到初始归并段输出文件的 归并段 2 中

首先在内存工作区中选出最小的，即元素“2”，放到归并段 2 中：

我们再从初始待排序文件中拿一个补上，即元素“19”：

再在内存工作区中选出最小的，即元素“3”，放到归并段 2 中：

我们再从初始待排序文件中拿一个补上，即元素“20”：

再在内存工作区中选出最小的，即元素“10”，放到归并段 2 中：

我们再从初始待排序文件中拿一个补上，即元素“17”：

再在内存工作区中选出最小的，即元素“17”，放到归并段 2 中：

我们再从初始待排序文件中拿一个补上，即元素“1”：

再在内存工作区中选出最小的，即元素“1”

但是！！！此时我们还是发现，元素“1”如果放到 归并段 2 中，那归并段 2 就不是递增的了，所以这个元素不能放到 归并段 2 中。

故我们把它留在内存工作区中，不管它：

我们在不管元素“1”的情况下，再在内存工作区中选出最小的，即元素“19”，放到归并段 2 中：

我们再从初始待排序文件中拿一个补上，即元素“23”：

我们在不管元素“1”的情况下，再在内存工作区中选出最小的，即元素“20”

我们再从初始待排序文件中拿一个补上，即元素“5”：

我们在不管元素“1”的情况下，再在内存工作区中选出最小的，即元素“5”

但是！！！此时我们又会发现，元素“5”如果放到 归并段 2 中，那归并段 2 就不是递增的了，所以这个元素不能放到 归并段 2 中。

故我们把它留在内存工作区中，也不管它：

我们在不管元素“1”、元素“5”的情况下，再在内存工作区中选出最小的，即元素“23”：

我们再从初始待排序文件中拿一个补上，即元素“36”：

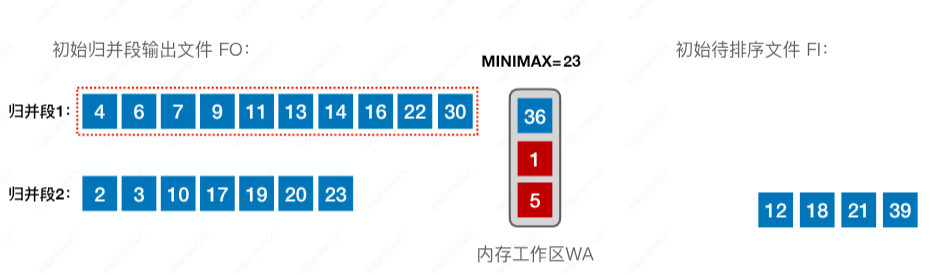
我们在不管元素“1”、元素“5”的情况下，再在内存工作区中选出最小的，即元素“36”：

我们再从初始待排序文件中拿一个补上，即元素“12”：

我们在不管元素“1”、元素“5”的情况下，再在内存工作区中选出最小的，即元素“12”

但是！！！此时我们又会发现，元素“12”如果放到 归并段 2 中，那归并段 2 就不是递增的了，所以这个元素不能放到 归并段 2 中。

故我们也把它留在内存工作区中，也不管它。

BUT此时我们发现，这个内存工作区一共就这么大，现在里面三个元素我们都不管了，那占着也没法让别的元素过来，所以我们现在的 归并段 2 到此结束，让这三个元素再开一个 归并段 3：

归并段 2 就此落幕：

我们把最小的元素“置换”出去，即放到初始归并段输出文件的 归并段 3 中

首先在内存工作区中选出最小的，即元素“1”，放到归并段 3 中：

我们再从初始待排序文件中拿一个补上，即元素“18”：

再在内存工作区中选出最小的，即元素“5”，放到归并段 3 中：

我们再从初始待排序文件中拿一个补上，即元素“21”：

再在内存工作区中选出最小的，即元素“12”，放到归并段 3 中：

我们再从初始待排序文件中拿一个补上，即元素“39”：

我们看到初始待排序文件里面已经空了，没东西了，拿最小的发现都比归并段3 中的最大元素大，所以可以直接把内存工作区里面的所有放到归并段 3 中：

我们的置换-选择排序就完成了。

当然，我们刚刚描述的生成初始归并段的过程，输出文件FO虽然是磁盘，但是不是选出一个就要写一次磁盘，而是我们有一个输出缓冲区，凑够了一块的内容，再把块写进磁盘，因为我们内外存交换是以块为单位的嘛。

还有我们从初始待排序文件FI中读入文件，也不是每次读入一个记录，而是也读入一块儿的内容，一次读入很多歌记录，只不过是每次都只会把一个记录给挪到内存工作区。

可以看到这个置换-选择排序还是很容易理解的，“选择”就是每次在内存工作区中选择一个最小的值，“置换”就是把选择的更小的值从内存工作区中置换出去，就是这样。

那我们现在再来看一下“置换-选择排序”的定义，也很容易看懂了：

设初始待排序文件为FI，初始归并段输出文件为FO，内存工作区为WA，FO和WA初始状态为空，WA棵容纳w个记录

1. 从FI输入w个记录到工作区WA；
2. 从WA中选出其中关键字取最小值的记录，记为MINMAX记录；
3. 将MINMAX记录输出到FO中去；
4. 若FI不空，则从FI输入下一个记录到WA中；
5. 从WA中所有关键字比MINMAX记录的关键字大的记录中选取最小关键字记录，作为新的MINMAX记录；
6. 重复 3~5，直至在WA中选不出新的MINMAX记录位置，由此得到一个初始归并段，输出一个归并段的结束标志到FO中去；
7. 重复 2~6，直至WA为空。由此得到全部初始归并段。

二、最佳归并树

1.归并树

假如我们有 5 个初始归并段，下面的圈圈里面就是每个归并段占多少块（假设每个归并段里面的数据都很多很多），我们两两进行 “2路”归并，发现还剩一个单的：

再把两两归并结果和那个单的归并：

那么就归并完成了。

上面标的读写的意思是，比如 R₂ 和 R₃ 进行归并，我们看到一个占了 5 块，一个占了 1 块，那读写就要进行 （5+1）* 2 次，因为一次只能读/写一个块嘛。

所以 R₂ 和 R₃ 进行归并，读写就进行了（5+1）* 2 次；

所以 R₄ 和 R₅ 进行归并，读写就进行了（6+2）* 2 次；

所以 R₂ 和 R₃ 合并后的 与 R₄ 和 R₅ 合并后的 进行归并，读写就进行了（6+8）* 2 次；

所以 R₁ 和 R₂、 R₃、 R₄、 R₅合并后的 进行归并，读写就进行了（2+14）* 2 次。

所以一共读写了 (5+1）* 2 + （6+2）* 2 + （6+8）* 2 +（2+14）* 2 = 88 次。

那么我们现在不看这些，你看它像不像一棵二叉树

那么我们把 每个初始归并段 看作一个 叶子结点 ， 归并段的长度 作为 结点权值

则上面这棵归并树的 带权路径长度 WPL = 2 * 1 + (5 + 1 + 6 + 2) * 3 = 44 = 读磁盘的次数 = 写磁盘的次数

所以 归并过程中的 磁盘 I/O 次数 = 归并树的WPL * 2

发现没？所以我们要想 让磁盘 I/O 次数最少，就要使归并树 WPL 最小

怎么让 WPL 最小？

哈夫曼树啊！！！

2.构造最佳归并树

我们还是把 每个初始归并段 看作一个 叶子结点 ， 归并段的长度 作为 结点权值 ，这次来构造一棵哈夫曼树，就是这个样子：

这就是我们的最佳归并树了。

最佳归并树 WPL_min = （1+2）* 4 + 2 * 3 + 5 * 2 + 6 * 1 = 34

读磁盘次数 = 写磁盘次数 = 34次

总的磁盘 I/O 次数 = 68

是不是比我们刚刚的 88 次要小很多

所以我们最佳归并树说的那么高大上，其实就是哈夫曼树罢辽。

那我们来看多路归并的情况，下面是 “3路”归并，随便归并的：

可以看到我们的 WPL = （9 + 30 + 12 + 18 + 3 + 17 + 2 + 6 + 24）× 2 = 242

归并过程中 磁盘 I/O 总次数 = 484 次

我们现在来构造3叉哈夫曼树，这是初始“叶子结点”：

选出三个结点权值最小的，分别是“2”、“3”、“6”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“11”也当做一个结点，选出三个结点权值最小的，分别是“9”、“11”、“12”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“32”也当做一个结点，选出三个结点权值最小的，分别是“17”、“18”、“24”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“59”也当做一个结点，选出三个结点权值最小的，分别是“30”、“32”、“59”，合并为一个新结点，权值为三个节点之和，就是这样：

那么我们的 WPL_min = （2 + 3 + 6） * 3 + （9 + 12 + 17 + 24 + 18） * 2 + 30 * 1 = 223

归并过程中 磁盘 I/O 总次数 = 446 次

比之前 484 次也是小很多。

上面这棵树就是我们“3路”归并的 最佳归并树 了，其实和“2路”归并构造 最佳归并树 的过程是一毛一样的。

3.虚段

这是我们刚刚“3路”归并的所有初始归并段：

如果我们“3路”归并的初始归并段减少一个，即我们把“30”这个归并段去掉，再建立我们的最佳归并树

先选出三个结点权值最小的，分别是“2”、“3”、“6”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“11”也当做一个结点，选出三个结点权值最小的，分别是“9”、“11”、“12”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“32”也当做一个结点，选出三个结点权值最小的，分别是“17”、“18”、“24”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“59”也当做一个结点，选出三个结点权值最小的

但是没有三个，只剩两个了

所以就选出“32”、“59”，合并为一个新结点，权值为两个节点之和，就是这样：

那么我们的 WPL_min = （2 + 3 + 6） * 3 + （9 + 12 + 17 + 24 + 18） * 2 = 193

归并过程中 磁盘 I/O 总次数 = 386 次

但是！！！这个可不是最佳归并树。为啥呢？因为你看我们最后一次只合并了两个结点，那是不是相当于合并了三个结点，只是最后一个结点是 0 而已

但是 结点权值是 0 的话，比所有权值都小，这也不应该等到最后才合并，反而应该是初始就合并才对，这样构造的才是权值最小的最佳归并树。

所以，对于 k 叉归并，如果 初始归并段的数量无法构成严格的 k 叉归并树，则需要补充几个长度为 0 的“虚段”，再进行 k 叉哈夫曼树的构造

对于上面的例子，我们缺 1 个“虚段”，加上一个就可以进行正常的“3路”归并了

所以我们添加 1 个“虚段”：

现在开始建立我们的最佳归并树

先选出三个结点权值最小的，分别是“0”、“2”、“3”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“5”也当做一个结点，选出三个结点权值最小的，分别是“5”、“6”、“9”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“20”也当做一个结点，选出三个结点权值最小的，分别是“12”、“17”、“18”，合并为一个新结点，权值为三个节点之和，就是这样：

再把合并后的结点“47”也当做一个结点，选出三个结点权值最小的，分别是“20”、“24”、“47”，合并为一个新结点，权值为三个节点之和，就是这样：

那么我们的 WPL_min = （2 + 3 + 0） * 3 + （6 + 9 + 12 + 17 + 18） * 2 + 24 * 1 = 163

归并过程中 磁盘 I/O 总次数 = 326 次

比上面的 386 次 更加少了

这才是我们针对缺了一个的归并段的集合“3路”归并生成的 最佳归并树。

4.虚段的数量

我们刚刚说了，对于 k 叉归并（k ＞ 2），如果 初始归并段的数量无法构成严格的 k 叉归并树，则需要补充几个长度为 0 的“虚段”，再进行 k 叉哈夫曼树的构造

那么我们到底要补几个虚段？

我们知道，k 叉的最佳归并树一定是一棵严格的 k 叉树，即树中只包含 度为 k，度为 0 的结点

设 度为 k 的结点有 n_k 个，度为 0 的结点有 n₀ 个，归并树总结点数 = n

则显然 初始归并段数量 + 虚段数量 = n₀

因为这倒过来的树，除了叶子结点，就没人 度为0 了，而我们又添加了虚段，虚段也算是叶子结点，所以就是 初始归并段数量 + 虚段数量 = n₀ 了；

又因为我们 所有结点要么 度为0，要么 度为k，所以 度为0 的结点个数 加上 度为k 的结点个数 就是我们的结点总数了，即：

n = n₀ + n_k

还有，我们最佳归并树正着放，就会发现除了根结点，每一个结点头上都插了一根线，一个线就是一个“度”，一共有 n 个结点，除了根结点， n-1 根结点头上都有线，所以总的度就是 n-1；又因为我们 度为k 的结点个数为 n_k，度为0 的结点个数为 n₀，所以我们结点和度的关系就是：

k * n_k = n - 1

由上述两个标紫色的可以得到——> n₀ = (k-1)n_k + 1

即 n_k = (n₀ - 1) / (k - 1)

n_k 是什么？是我们度为 k 的结点个数。

在一个严格的 k 叉树里面，除了叶子结点的所有结点一定都是 度为k 的。所以也就是说，当 (n₀ - 1) / (k - 1) 为一个整数的时候，那就说明 n_k 是一个正常的整数值

也就是说此时可以构成一棵严格的 k 叉树

所以：

• 若（初始归并段数量 - 1）% （k-1）= 0，说明刚好可以构成严格 k 叉树，此时不需要添加虚段；
• 若（初始归并段数量 - 1）% （k-1）= u ≠ 0，需补充 （k-1）- u 个虚段

举个栗子，比如我们“8路”归并，现在有 19 个初始归并段，求我们需要添加虚段的数量。

现在我们 （初始归并段数量 - 1）% （k-1）=（19 - 1）% （8-1）= 18 % 7 = 4 ≠ 0，所以要添加虚段；

添加虚段的数量是 （k-1）- u 个，也就是 （8-1）- 4 个，即 3 个，所以添加三个虚段就可以了。

验证一下，n_k = (n₀ - 1) / (k - 1) = (19 + 3 - 1) / (8 - 1) = 21 / 7 = 3，能除得尽，所以没毛病。

总结

所谓“置换-选择排序”，“选择”就是每次在内存工作区中选择一个最小的值，“置换”就是把选择的更小的值从内存工作区中置换出去

置换-选择排序得到的归并段长度不一，这些初始归并段的长度可以超过内存工作区的长度限制，因为初始归并段长度越大，初始归并段个数越少，读写磁盘数就越少嘛。

我们最佳归并段其实就是构造一棵哈夫曼树，因为这样可以使它的WPL最小，WPL的值是读写磁盘数的一半。

但是有时候需要添加“虚段”，有时候不用，这时我们就看 （初始归并段数量 - 1）% （k-1）的值，要是0就不用添加，要是 u 就添加（k-1）- u 个就行了。