六种经典排序算法：从原理到 Java 实现

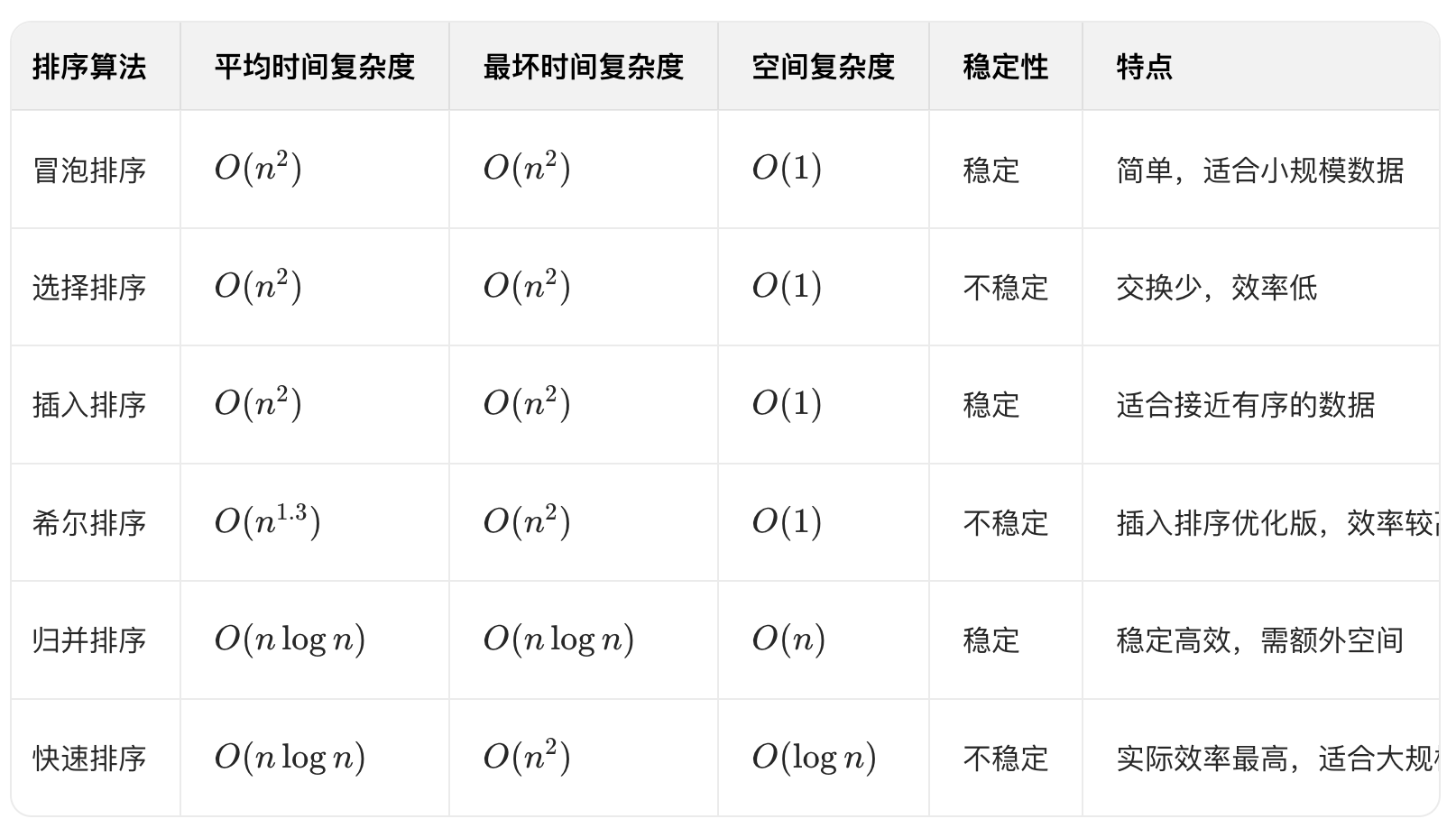
总结对比表

java代码实现

public class SortingAlgorithms {

    // 1. 冒泡排序
    public static void bubbleSort(int[] arr) {
        int n = arr.length;
        boolean swapped;
        for (int i = 0; i < n - 1; i++) {
            swapped = false;
            for (int j = 0; j < n - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    // 交换 arr[j] 和 arr[j+1]
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    swapped = true;
                }
            }
            // 如果没有发生交换，说明数组已经有序
            if (!swapped) break;
        }
    }

    // 2. 选择排序
    public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            // 交换 arr[i] 和 arr[minIndex]
            if (minIndex != i) {
                int temp = arr[i];
                arr[i] = arr[minIndex];
                arr[minIndex] = temp;
            }
        }
    }

    // 3. 插入排序
    public static void insertionSort(int[] arr) {
        int n = arr.length;
        for (int i = 1; i < n; i++) {
            int key = arr[i];
            int j = i - 1;
            // 将比key大的元素后移
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j--;
            }
            arr[j + 1] = key; // 插入key
        }
    }

    // 4. 希尔排序
    public static void shellSort(int[] arr) {
        int n = arr.length;
        // 初始步长为数组长度的一半，逐渐减半
        for (int gap = n / 2; gap > 0; gap /= 2) {
            // 对每个子数组进行插入排序
            for (int i = gap; i < n; i++) {
                int temp = arr[i];
                int j;
                for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                    arr[j] = arr[j - gap];
                }
                arr[j] = temp;
            }
        }
    }

    // 5. 归并排序
    public static void mergeSort(int[] arr) {
        if (arr.length <= 1) return;
        int[] temp = new int[arr.length];
        mergeSort(arr, temp, 0, arr.length - 1);
    }

    private static void mergeSort(int[] arr, int[] temp, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;
            mergeSort(arr, temp, left, mid);
            mergeSort(arr, temp, mid + 1, right);
            merge(arr, temp, left, mid, right);
        }
    }

    private static void merge(int[] arr, int[] temp, int left, int mid, int right) {
        // 复制到临时数组
        System.arraycopy(arr, left, temp, left, right - left + 1);

        int i = left;      // 左子数组指针
        int j = mid + 1;   // 右子数组指针
        int k = left;      // 结果数组指针

        while (i <= mid && j <= right) {
            if (temp[i] <= temp[j]) {
                arr[k] = temp[i];
                i++;
            } else {
                arr[k] = temp[j];
                j++;
            }
            k++;
        }

        // 复制左子数组剩余元素
        while (i <= mid) {
            arr[k] = temp[i];
            i++;
            k++;
        }
        // 右子数组剩余元素无需复制，已在原位置
    }

    // 6. 快速排序
    public static void quickSort(int[] arr) {
        quickSort(arr, 0, arr.length - 1);
    }

    private static void quickSort(int[] arr, int left, int right) {
        if (left < right) {
            int pivotIndex = partition(arr, left, right);
            quickSort(arr, left, pivotIndex - 1);
            quickSort(arr, pivotIndex + 1, right);
        }
    }

    private static int partition(int[] arr, int left, int right) {
        int pivot = arr[right];  // 选择最后一个元素作为基准
        int i = left - 1;        // 小于基准的元素边界

        for (int j = left; j < right; j++) {
            if (arr[j] < pivot) {
                i++;
                // 交换 arr[i] 和 arr[j]
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }

        // 将基准放到正确位置
        int temp = arr[i + 1];
        arr[i + 1] = arr[right];
        arr[right] = temp;

        return i + 1;  // 返回基准的位置
    }

    // 测试代码
    public static void main(String[] args) {
        int[] arr = {5, 3, 8, 4, 2};
        
        System.out.println("原始数组:");
        printArray(arr);

        // 选择排序算法测试
        int[] arrCopy = arr.clone();
        quickSort(arrCopy);  // 替换为其他排序方法测试
        
        System.out.println("\n排序后数组:");
        printArray(arrCopy);
    }

    private static void printArray(int[] arr) {
        for (int num : arr) {
            System.out.print(num + " ");
        }
        System.out.println();
    }
}

一、冒泡排序（Bubble Sort）

基本思想

通过重复遍历待排序数组，每次比较相邻的两个元素，若它们的顺序错误（如从小到大排序时前一个比后一个大），则交换它们的位置。遍历过程中，较大的元素会像 “气泡” 一样逐渐 “浮” 到数组的末尾，因此得名。

实现步骤

1. 从数组的第一个元素开始，依次比较相邻的两个元素（索引 i 和 i+1）。
2. 若前一个元素大于后一个元素，交换两者位置。
3. 完成一轮遍历后，最大的元素会移动到数组的末尾。
4. 忽略已排好序的末尾元素，重复上述过程，直到整个数组有序。

示例（从小到大排序）

原始数组：[5, 3, 8, 4, 2]

• 第 1 轮：比较 5&3（交换→[3,5,8,4,2]）→5&8（不换）→8&4（交换→[3,5,4,8,2]）→8&2（交换→[3,5,4,2,8]），最大元素 8 到位。
• 第 2 轮：比较 3&5（不换）→5&4（交换→[3,4,5,2,8]）→5&2（交换→[3,4,2,5,8]），第二大元素 5 到位。
• 第 3 轮：比较 3&4（不换）→4&2（交换→[3,2,4,5,8]），第三大元素 4 到位。
• 第 4 轮：比较 3&2（交换→[2,3,4,5,8]），第四大元素 3 到位，数组有序。

复杂度

• 时间复杂度：
  • 最坏情况（逆序）：O(n^2)（需遍历 (n-1) 轮，每轮比较 (n-i) 次）。
  • 最好情况（已排序）：O(n)（优化后，若一轮无交换则提前结束）。
• 空间复杂度：O(1)（仅需常数级临时变量）。

特点

• 稳定排序（相等元素相对位置不变）。
• 简单直观，但效率较低，适合小规模数据。

二、选择排序（Selection Sort）

基本思想

每一轮从待排序的元素中找到最小（或最大）的元素，将其与待排序部分的第一个元素交换位置，直到所有元素排序完成。

实现步骤

1. 遍历数组，找到最小元素的索引，与数组第一个元素交换。
2. 从剩余未排序元素中找到最小元素，与剩余部分的第一个元素交换。
3. 重复上述过程，直到所有元素有序。

示例（从小到大排序）

原始数组：[5, 3, 8, 4, 2]

• 第 1 轮：找最小元素 2（索引 4），与第一个元素 5 交换→[2, 3, 8, 4, 5]。
• 第 2 轮：从剩余[3,8,4,5]中找最小 3（索引 1），无需交换→[2,3,8,4,5]。
• 第 3 轮：从剩余[8,4,5]中找最小 4（索引 3），与 8 交换→[2,3,4,8,5]。
• 第 4 轮：从剩余[8,5]中找最小 5（索引 4），与 8 交换→[2,3,4,5,8]，数组有序。

复杂度

• 时间复杂度：O(n^2)（无论数组是否有序，都需 n-1 轮遍历，每轮比较 n-i 次）。
• 空间复杂度：O(1)（仅需常数级临时变量）。

特点

• 不稳定排序（例如 [2, 2, 1]，第一轮会将 1 与第一个 2 交换，破坏稳定性）。
• 交换次数少（每轮最多 1 次），但比较次数多，适合数据量小的场景。

三、插入排序（Insertion Sort）

基本思想

将数组分为 “已排序” 和 “未排序” 两部分，每次从 “未排序” 部分取一个元素，插入到 “已排序” 部分的合适位置，使 “已排序” 部分始终有序。

实现步骤

1. 默认第一个元素为 “已排序” 部分。
2. 从第二个元素开始，作为待插入元素，与 “已排序” 部分从后往前比较。
3. 若待插入元素小于当前比较元素，将当前元素后移；否则，插入待插入元素到当前位置后。
4. 重复上述过程，直到所有元素插入完成。

示例（从小到大排序）

原始数组：[5, 3, 8, 4, 2]

• 第 1 步：“已排序” 为[5]，待插入 3。3<5→5 后移，插入 3→[3,5,8,4,2]。
• 第 2 步：待插入 8。8>5→直接插入→[3,5,8,4,2]。
• 第 3 步：待插入 4。4<8→8 后移；4<5→5 后移；4>3→插入 4→[3,4,5,8,2]。
• 第 4 步：待插入 2。2<8→8 后移；2<5→5 后移；2<4→4 后移；2<3→3 后移，插入 2→[2,3,4,5,8]。

复杂度

• 时间复杂度：
  • 最坏情况（逆序）：O(n^2)（每轮插入需移动 i 个元素）。
  • 最好情况（已排序）：O(n)（无需移动元素，仅需遍历）。
• 空间复杂度：O(1)（仅需常数级临时变量）。

特点

• 稳定排序。
• 适合小规模数据或接近有序的数据（效率高于冒泡和选择排序）。

四、希尔排序（Shell Sort）

基本思想

插入排序的优化版，通过分组插入排序减少元素移动次数。先将数组按一定 “步长” 分为多个子数组，对每个子数组进行插入排序；逐渐减小步长，重复分组排序，直到步长为 1（此时为普通插入排序）。

实现步骤

1. 选择初始步长（通常为数组长度的一半，如 gap = n/2 ）。
2. 按步长将数组分为 gap 个子数组，对每个子数组进行插入排序。
3. 减小步长（如 gap = gap/2 ），重复步骤 2，直到步长为 1。
4. 步长为 1 时，对整个数组进行插入排序，完成排序。

示例（从小到大排序，步长初始为 2）

原始数组：[12, 34, 54, 2, 3]

• 步长 = 2：子数组为[12,54,3]和[34,2]。
  • 子数组 1 插入排序→[3,54,12]；子数组 2 插入排序→[2,34]。
  • 合并后：[3,2,12,34,54]。
• 步长 = 1：对整个数组插入排序→[2,3,12,34,54]。

复杂度

• 时间复杂度：取决于步长选择，平均约为 O(n^{1.3})，最坏情况可优化至 O(n log2 n) )。
• 空间复杂度：O(1)（仅需常数级临时变量）。

特点

• 不稳定排序（分组排序可能破坏相等元素的相对位置）。
• 效率高于普通插入排序，适合中大规模数据。

五、归并排序（Merge Sort）

基本思想

基于 “分治法”：将数组不断二分，直到每个子数组只有 1 个元素（天然有序）；然后将相邻的子数组两两 “归并”，合并成一个有序数组，重复归并过程，最终得到完整的有序数组。

实现步骤

1. 分解：将数组从中间分为左右两个子数组，递归分解子数组，直到子数组长度为 1。
2. 合并：将两个有序子数组合并为一个有序数组（需临时数组辅助）。
   • 比较两个子数组的元素，将较小的元素放入临时数组。
   • 若一个子数组遍历完毕，将另一个子数组剩余元素直接放入临时数组。
   • 将临时数组的元素复制回原数组。

示例（从小到大排序）

原始数组：[8,4,5,7,1,3,6,2]

• 分解：[8,4,5,7] 和 [1,3,6,2]→继续分解为 [8,4]、[5,7]、[1,3]、[6,2]→再分解为单个元素。
• 合并：
  • [8]与[4]合并→[4,8]；[5]与[7]合并→[5,7]→合并为[4,5,7,8]。
  • [1]与[3]合并→[1,3]；[6]与[2]合并→[2,6]→合并为[1,2,3,6]。
  • 最终合并[4,5,7,8]和[1,2,3,6]→[1,2,3,4,5,6,7,8]。

复杂度

• 时间复杂度：O(n log n)（分解为 log n层，每层合并总耗时 O(n) ）。
• 空间复杂度：O(n)（需临时数组存储合并结果）。

特点

• 稳定排序。
• 适合大规模数据，不受输入数据影响（时间复杂度稳定），但需要额外空间。

六、快速排序（Quick Sort）

基本思想

基于 “分治法”：选择数组中的一个元素作为 “基准值（pivot）”，将数组分为两部分 —— 小于基准值的元素和大于基准值的元素；递归对两部分进行快速排序，最终合并为有序数组。

实现步骤

1. 选择基准值（通常选第一个、最后一个或中间元素）。
2. 分区：将小于基准值的元素放在基准值左侧，大于的放在右侧（相等元素可放任意一侧）。
3. 递归对基准值左侧和右侧的子数组重复步骤 1-2，直到子数组长度为 1 或 0。

示例（从小到大排序，基准值选第一个元素）

原始数组：[8,4,5,7,1,3,6,2]

• 基准值 = 8，分区后：小于 8 的[4,5,7,1,3,6,2]和大于 8 的[]，基准值 8 到位。
• 对[4,5,7,1,3,6,2]，基准值 = 4，分区后：[1,3,2]和[5,7,6]，4 到位。
• 递归处理[1,3,2]（基准值 1→[]和[3,2]）和[5,7,6]（基准值 5→[]和[7,6]）。
• 最终合并：[1,2,3,4,5,6,7,8]。

复杂度

• 时间复杂度：
  • 平均情况：O(n log n)（每次分区能将数组均分）。
  • 最坏情况（已排序且基准值选端点）：O(n^2)（每次分区后一个子数组长度为 (n-1) ）。
• 空间复杂度：O(log n)（递归栈空间，平均情况）或 O(n)（最坏情况）。

特点

• 不稳定排序（分区过程可能交换相等元素的位置）。
• 实际应用中效率最高的排序算法之一，适合大规模数据（可优化基准值选择避免最坏情况）。