【洛谷】The Blocks Problem、合并两个有序数组，补充pair(vector相关算法题p2)

88.合并两个有序数组

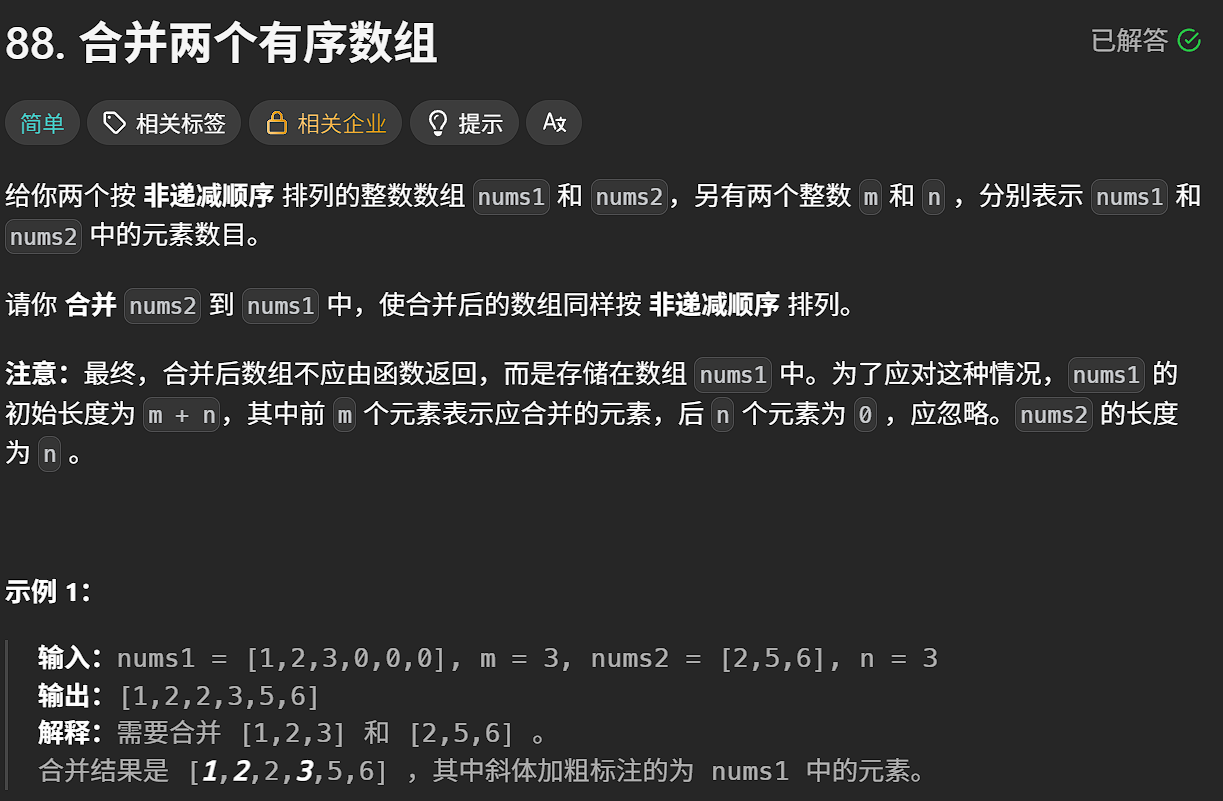
题目描述

题目解析

这道题有两个思路，一个是开辟一个m+n大小的数组然后遍历两个原数组按大小顺序尾插到新数组中，尾插完后再将新数组的值拷贝回原数组，但是这道题已经在第一个数组里为我们开好空间了，所以我们直接在原数组里操作就行了，思路是分别从两个数组的尾部开始遍历，因为从前遍历会发生数据的覆盖，跳出while循环后若是第二个数组还剩余，就将第二个数组中的数据拷贝到一数组。

代码

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int mcur = m - 1;
        int ncur = n - 1;
        int rcur = m + n - 1;
        while(mcur >= 0 && ncur >= 0)
        {
            if(nums1[mcur] > nums2[ncur])
            {
                nums1[rcur--] = nums1[mcur--];
            }
            else 
            {
                nums1[rcur--] = nums2[ncur--];
            }
        }
        
        while(ncur >= 0)
        {
            nums1[rcur--] = nums2[ncur--];
        }
    }
};

UVA101 The Blocks Problem

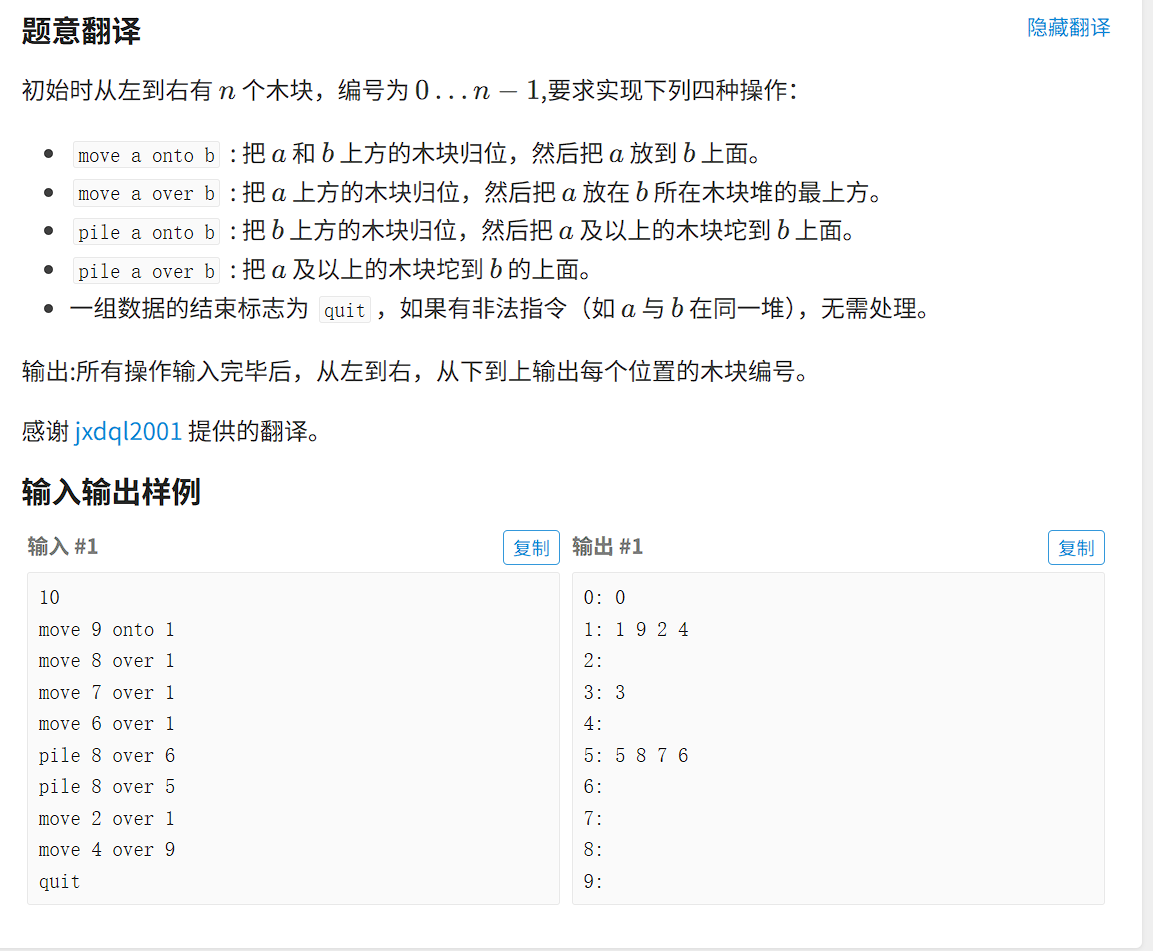
题目描述

题目解析

这道题会用到pair，所以小编先介绍一下什么是pair，原理不用深究，知道怎么用就行了。

这道题先理解题意，我们以样例来解释，一共有10个位置，每个位置有一个木块。我们可以把每个位置理解成一个槽，每个槽装着木块，经过一系列操作后每个槽有可能没有木块，也有可能有多个木块垒在一起，示意图如下：

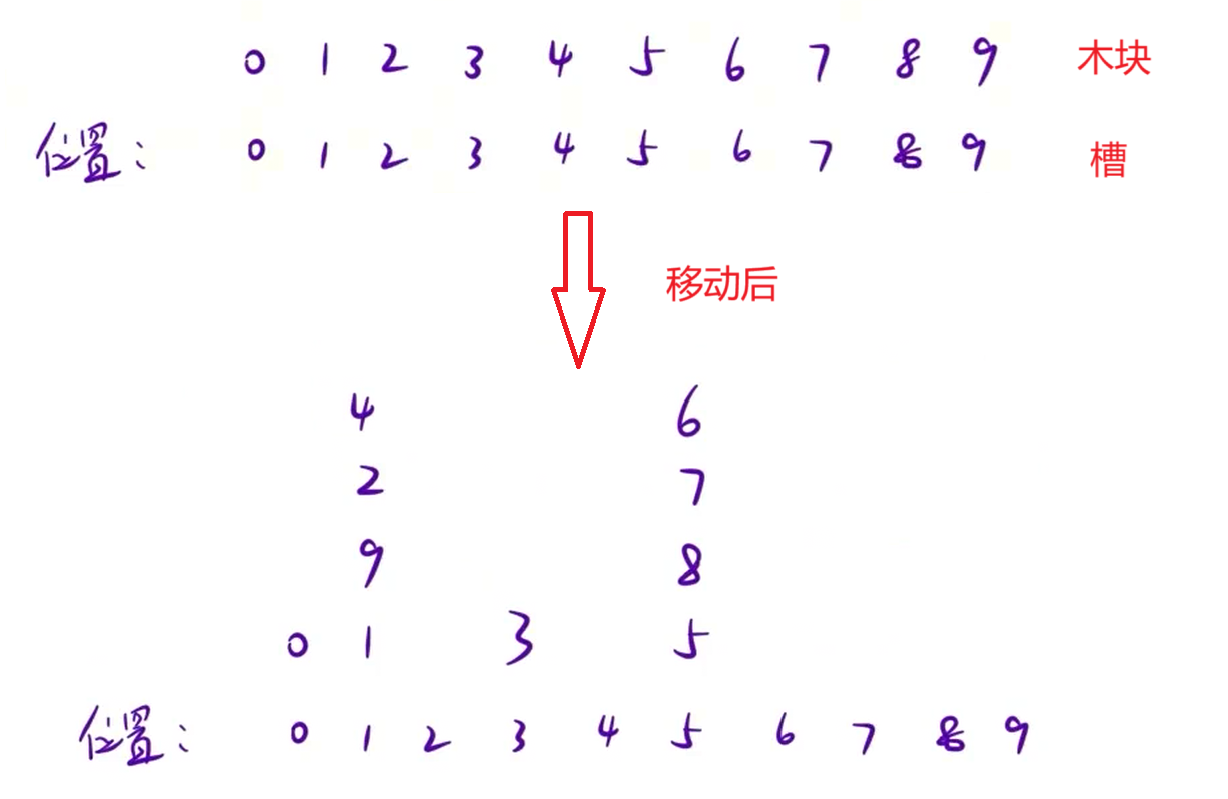
所以我们需要一个二维数组来存储数据，一维代表槽，二维代表槽中的木块，题目中说最多有25个木块也就是起始最多有25个槽，所以我们创建30个数组妥妥够了。
这道题看似有四个操作，其实总结就是两个，归位和移动，四个操作都有移动，所以我们每次循环都要移动，无非就是判断是否归位，我们分析题目知道当第一个单词为move需要将a上方木块归位，第二个单词为onto需要将b上方木块归位，所以我们需要写两个函数，归位clear和移动move，归位需要遍历a木块上方的所有木块，把木块尾插到木块初始的槽，木块本身的数值就是它其实槽的编号，move就是将a木块上方的木块及a木块全部尾插到b木块所在的槽。
而我们要执行上述两个操作首先需要先找到a b目标木块在哪，所以首先需要写一个find函数，这里find的返回值就需要用到pair，返回木块在哪个槽和在槽的哪个位置，需要注意题目要求当a与b在同一个槽是无需操作，所以我们在循环里需要加上这个判断，若为真就跳过当次循环。
而循环的设置也很有讲究，首先cin一个n读取木块数目，然后后续输入就一直都是 字符串 数字字符串数字的格式了，所以我们可以while(cin >> op1 >> a >> op2 >> b),当最后输入quit时由于不匹配就会跳出循环。
最后还需要依次打印结果。

代码

using namespace std;
#include <iostream>
#include <vector>

const int N = 30;
vector<int> v[N];
int n;

string op1, op2;
int a, b;
typedef pair<int, int> pii;

pii find(int x)
{
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < v[i].size(); j++)
		{
			if (v[i][j] == x)
			{
				return { i,j };
			}
		}
	}
}

void clear(int x1, int y1)
{
	//遍历a木块上方所有木块
	for (int i = y1 + 1; i < v[x1].size(); i++)
	{
		//pos是待归位木块在那个槽，也就是木块本身的值是多少
		int pos = v[x1][i];
		v[pos].push_back(pos);
	}
	//并没有真的移除数据，需要resize
	v[x1].resize(y1 + 1);
}

void move(int x1, int y1, int x2)
{
	//遍历目标木块及目标木块上方所有木块
	for (int i = y1; i < v[x1].size(); i++)
	{
		//将目标木块尾插到b木块所在位置
		v[x2].push_back(v[x1][i]);
	}
	v[x1].resize(y1);
}

int main()
{
	cin >> n;
	//初始化vector
	for (int i = 0; i < n; i++)
	{
		v[i].push_back(i);
	}

	while (cin >> op1 >> a >> op2 >> b)
	{
		//先找到a,b的位置
		pii p1 = find(a);
		int x1 = p1.first, y1 = p1.second;
		pii p2 = find(b);
		int x2 = p2.first, y2 = p2.second;

		//a与b在同一堆无需处理
		if (x1 == x2)
			continue;

		if (op1 == "move")
		{
			clear(x1,y1);
		}

		if (op2 == "onto")
		{
			clear(x2, y2);
		}

		move(x1, y1, x2);
	}

	for (int i = 0; i < n; i++)
	{
		cout << i << ':';
		for (int j = 0; j < v[i].size(); j++)
		{
			cout << " " << v[i][j];
		}
		cout << endl;
	}
	return 0;
}