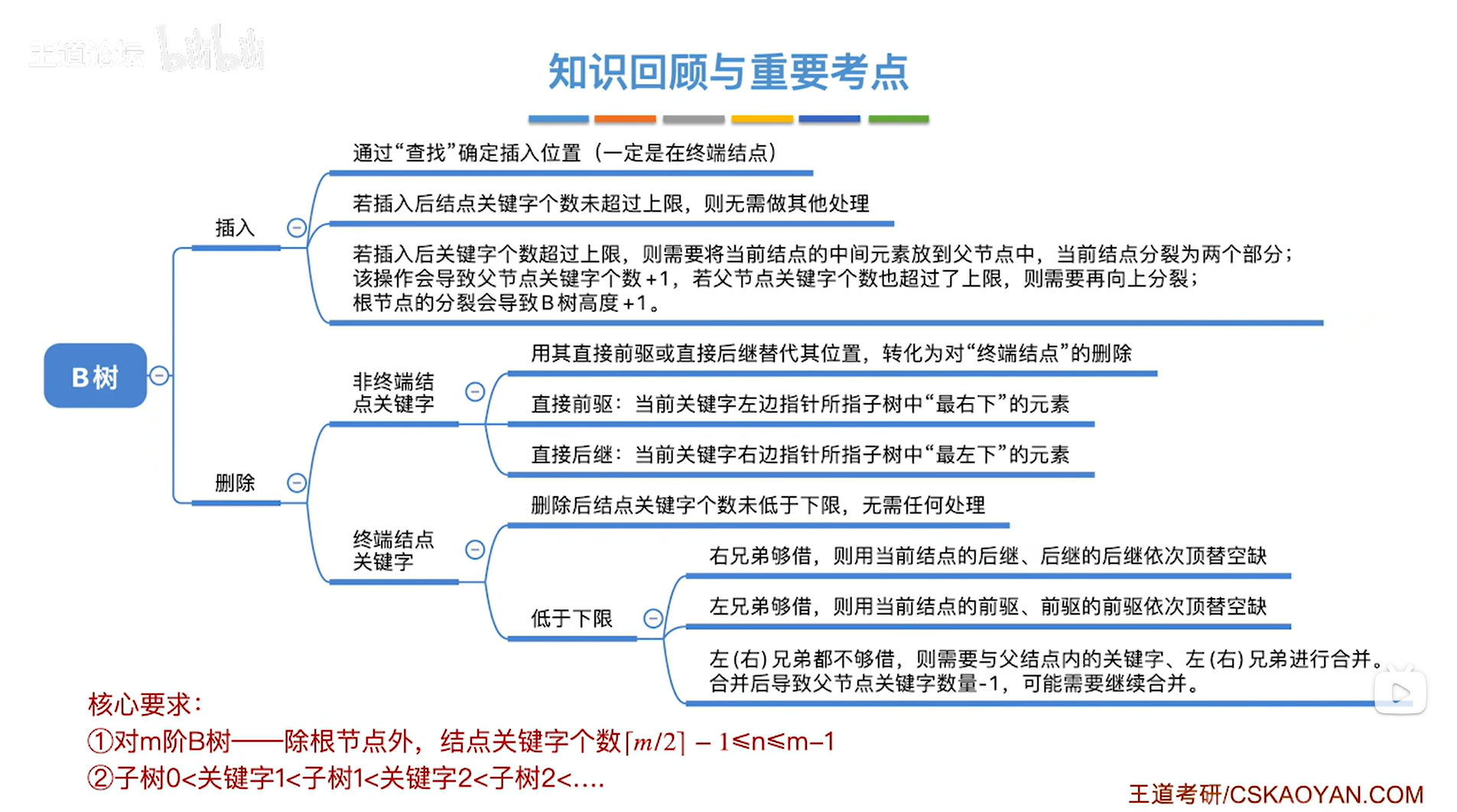
一.B树的插入:
1.实例:
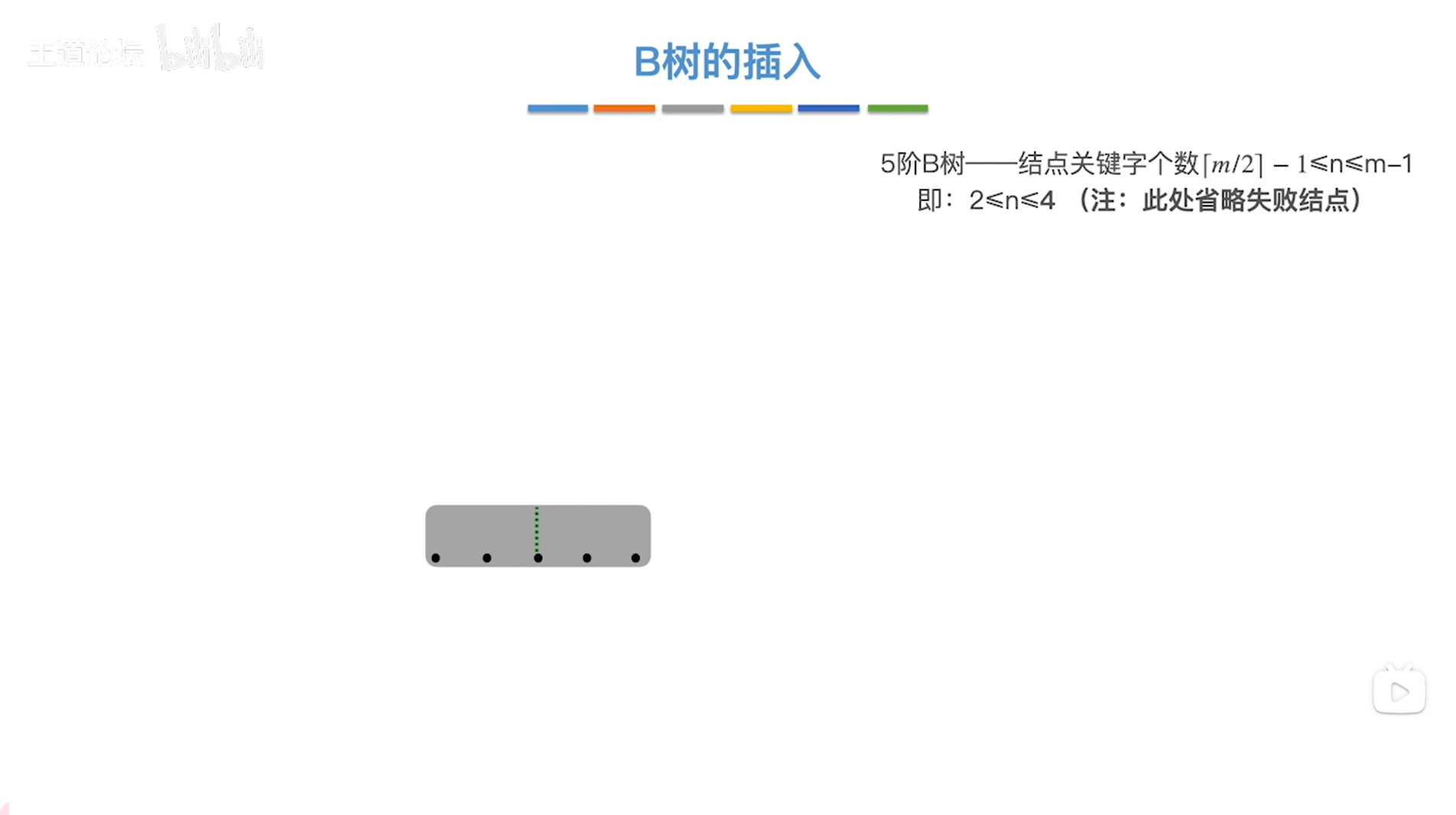
如上图,
从NULL开始建立一个B树,并且规定是一个5阶B树,也就是结点内的关键字个数至少为2个,至多为4个,且结点内的关键字要求按照递增排序,
现在插入关键字25,显然要放入根结点内,
如下图:
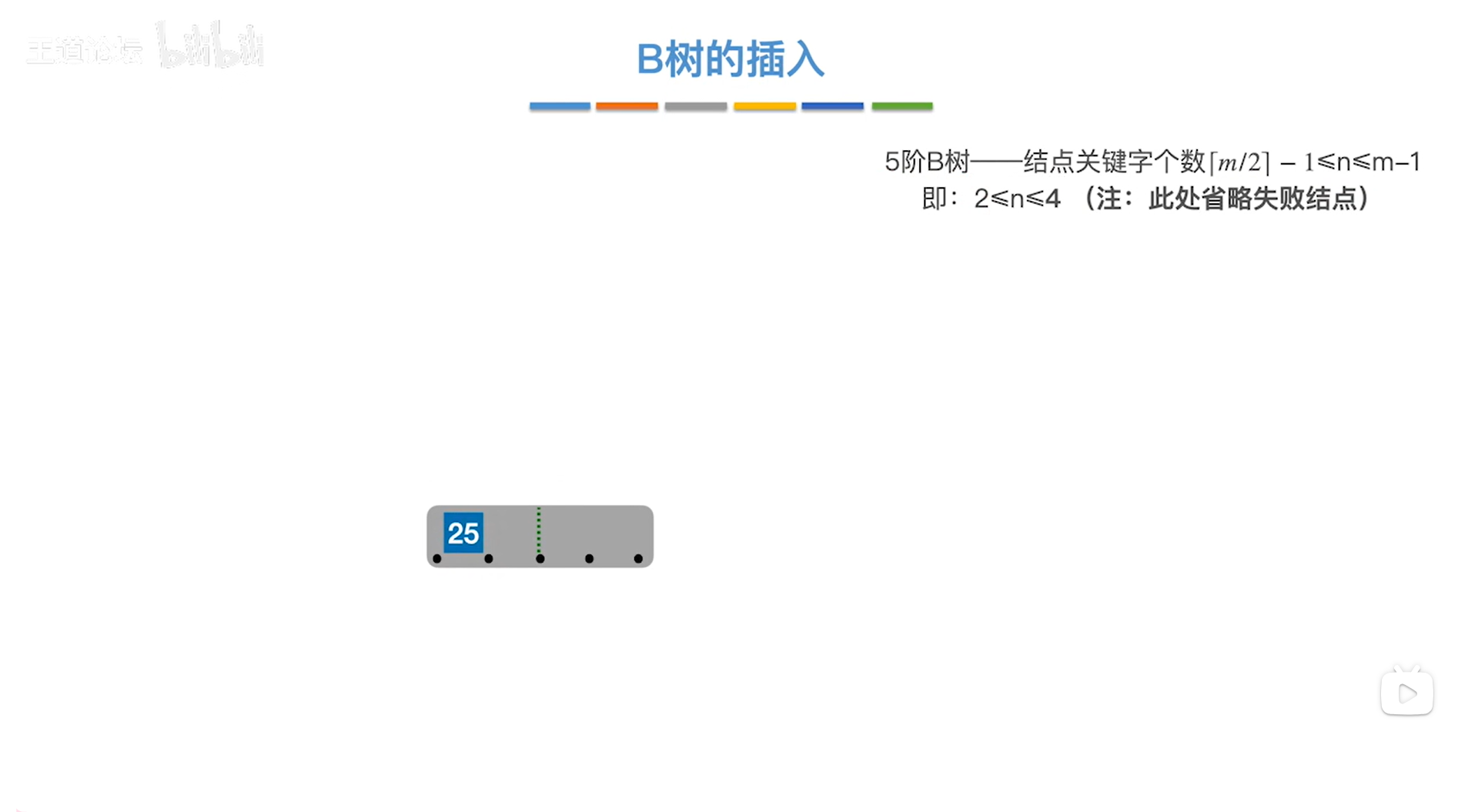
如上图,
当前处理的结点内只有1个关键字,根据"结点内的关键字个数至少为2个,至多为4个"接下来必须要在该结点内插入至少一个关键字
接下来插入关键字38,38比25更大,所以放到28的后面即可,
如下图:
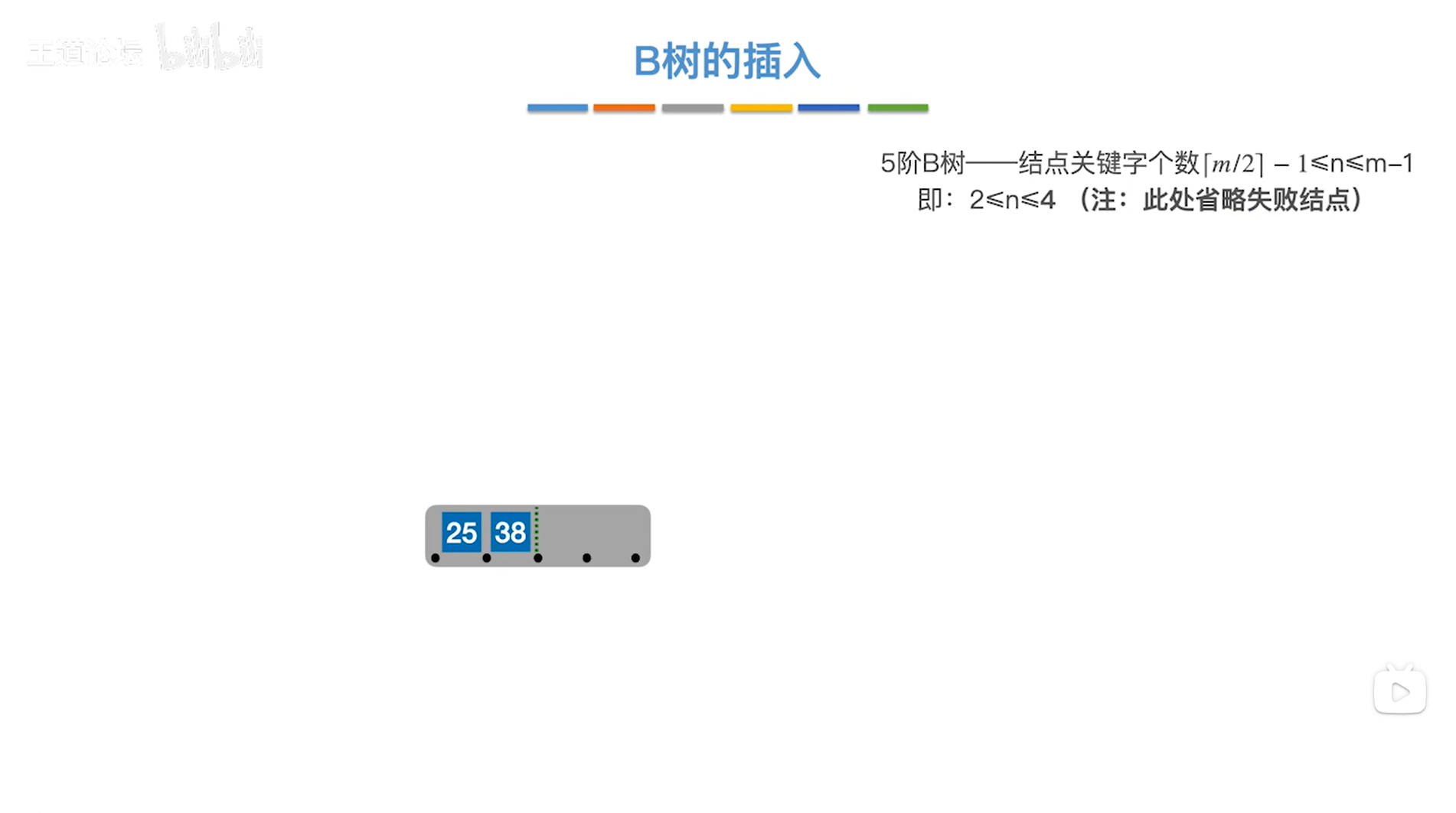
如上图,
当前处理的结点内有2个关键字,根据"结点内的关键字个数至少为2个,至多为4个"接下来可以在该结点内继续插入关键字,也可以建立一个新结点进行插入操作->现在选择"在该结点内继续插入关键字"
接下来插入关键字49,49比38更大,所以放到38的后面即可,
如下图:

如上图,
当前处理的结点内有3个关键字,根据"结点内的关键字个数至少为2个,至多为4个"接下来可以在该结点内继续插入关键字,也可以建立一个新结点进行插入操作->现在选择"在该结点内继续插入关键字"
接下来插入关键字60,60比49更大,所以放到49的后面即可,
如下图:

如上图,
当前处理的结点内有4个关键字,根据"结点内的关键字个数至少为2个,至多为4个"接下来只能建立一个新结点进行插入操作
因此接下来如果往当前结点即根结点内继续插入一个关键字80,就会导致根结点内关键字的个数超出4个,
注:这里先在当前结点即根结点内按照递增顺序插入关键字80,
如下图:

如上图,
对于这种情况,需要把当前结点即根结点分裂成2个结点,
分裂规则如下图:
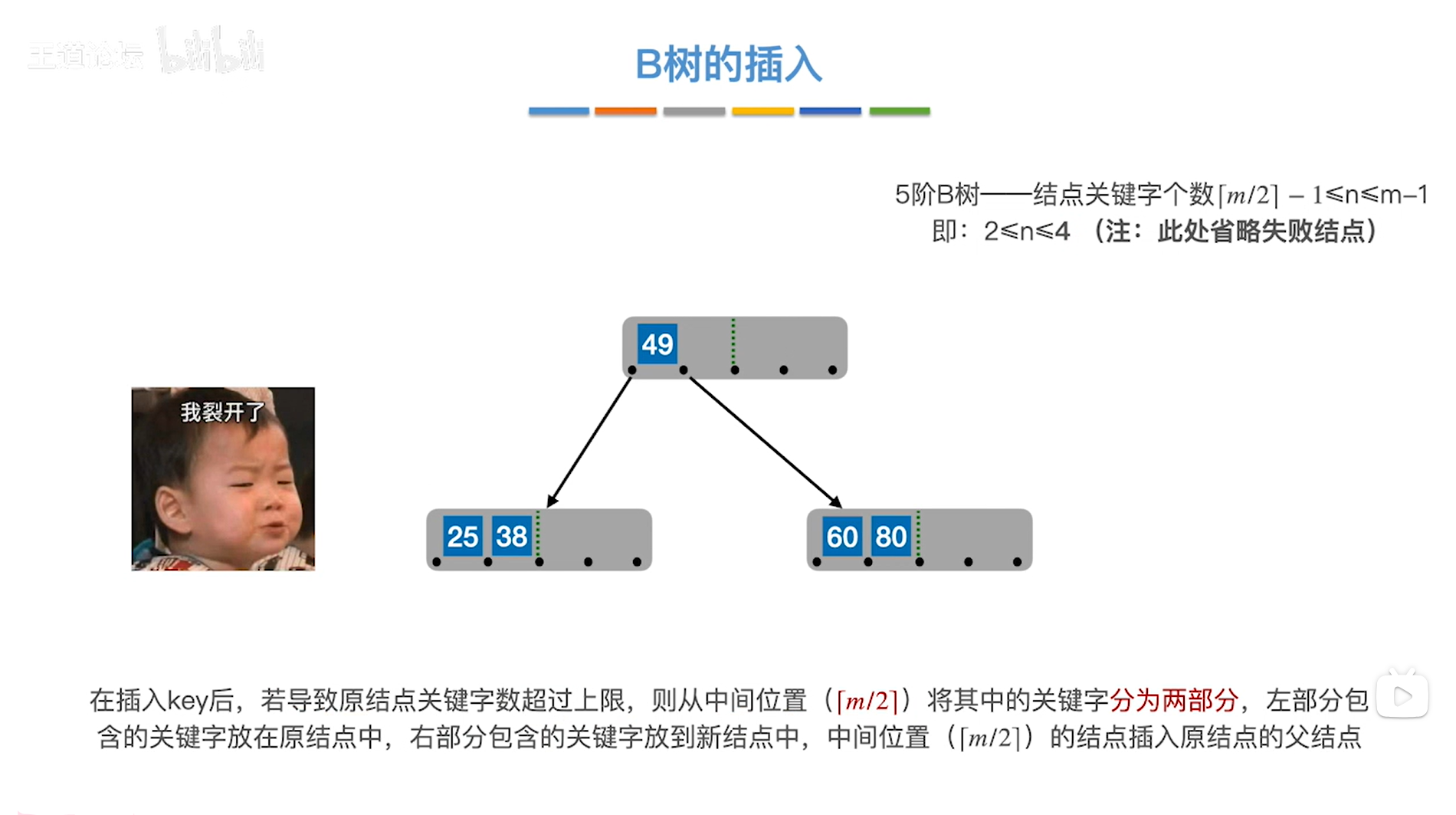
如上图,
接下来插入关键字90,
需要注意的是每一次新插入的元素一定是插入到最底层的终端结点中,用"查找"规则来确定插入位置(详情见"7.11.B树"),
从根结点出发,由于关键字90大于49,且49的右边已经没有关键字了,所以90要插在49的右孩子指针所指的子树中,
49的右孩子指针所指的子树中根结点包含的关键字为60、80,该结点内的关键字个数没有达到上限,所以可以继续插入关键字,接下来检查该结点内的关键字,
第一个关键字60比90更小,所以会检查下一个关键字80,
第二个关键字80比90更小,又因为80后已经没有关键字了,所以90应插在80的后面,
如下图:
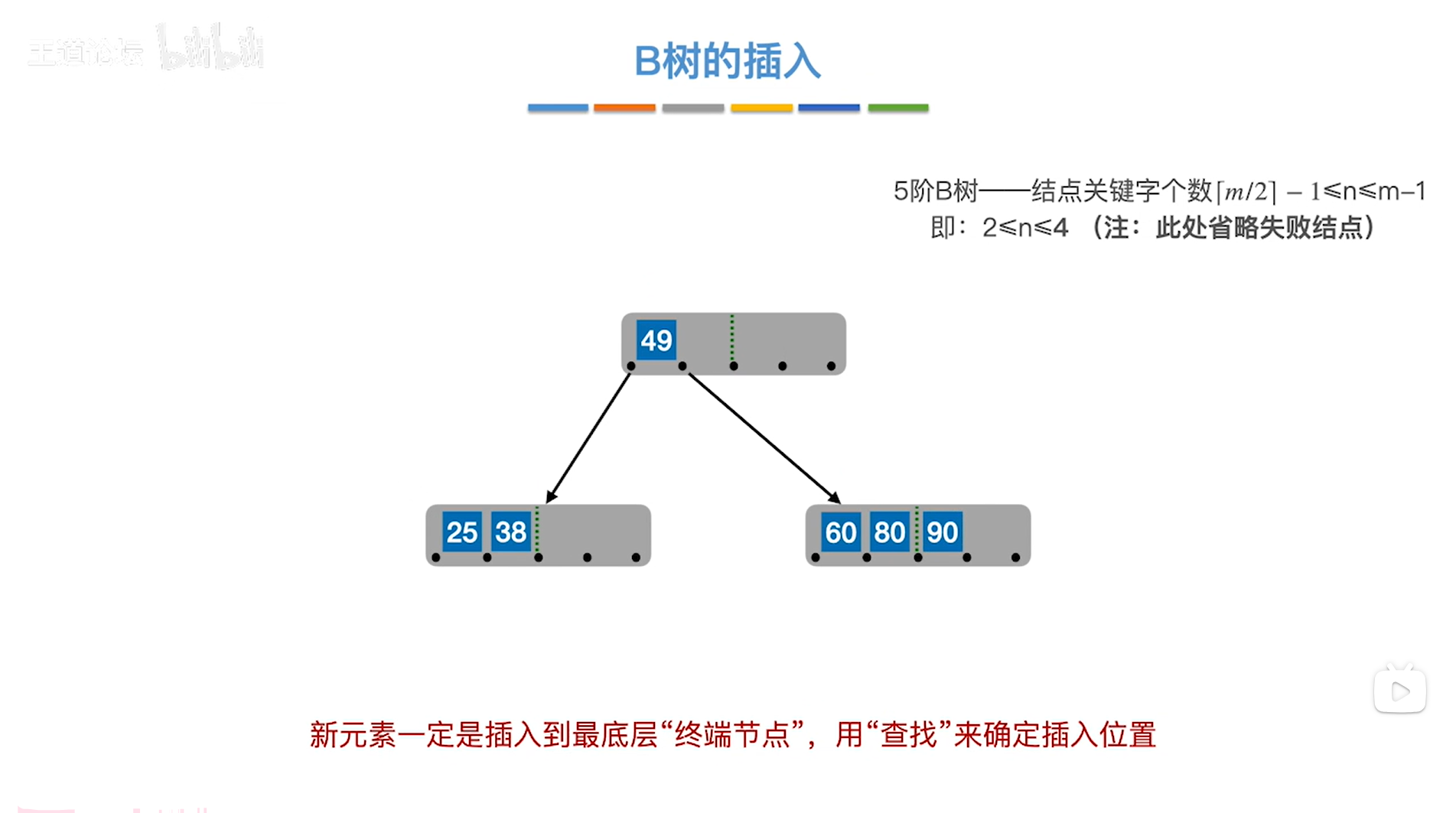
注:如果新插入的元素90没有插在终端结点而是插在根结点中,这显然是错误的,因为如果90插在根结点中,90就需要插在49的后面,由于90后面没有关键字了,因此90后面就是一个空指针NULL,也就是紫色的叶子结点,这时意味着B树中各个紫色的失败结点已经不属于同一层了,这样就不满足B树的特性了,所以新结点一定插入到最下面的终端结点中,
如下图:
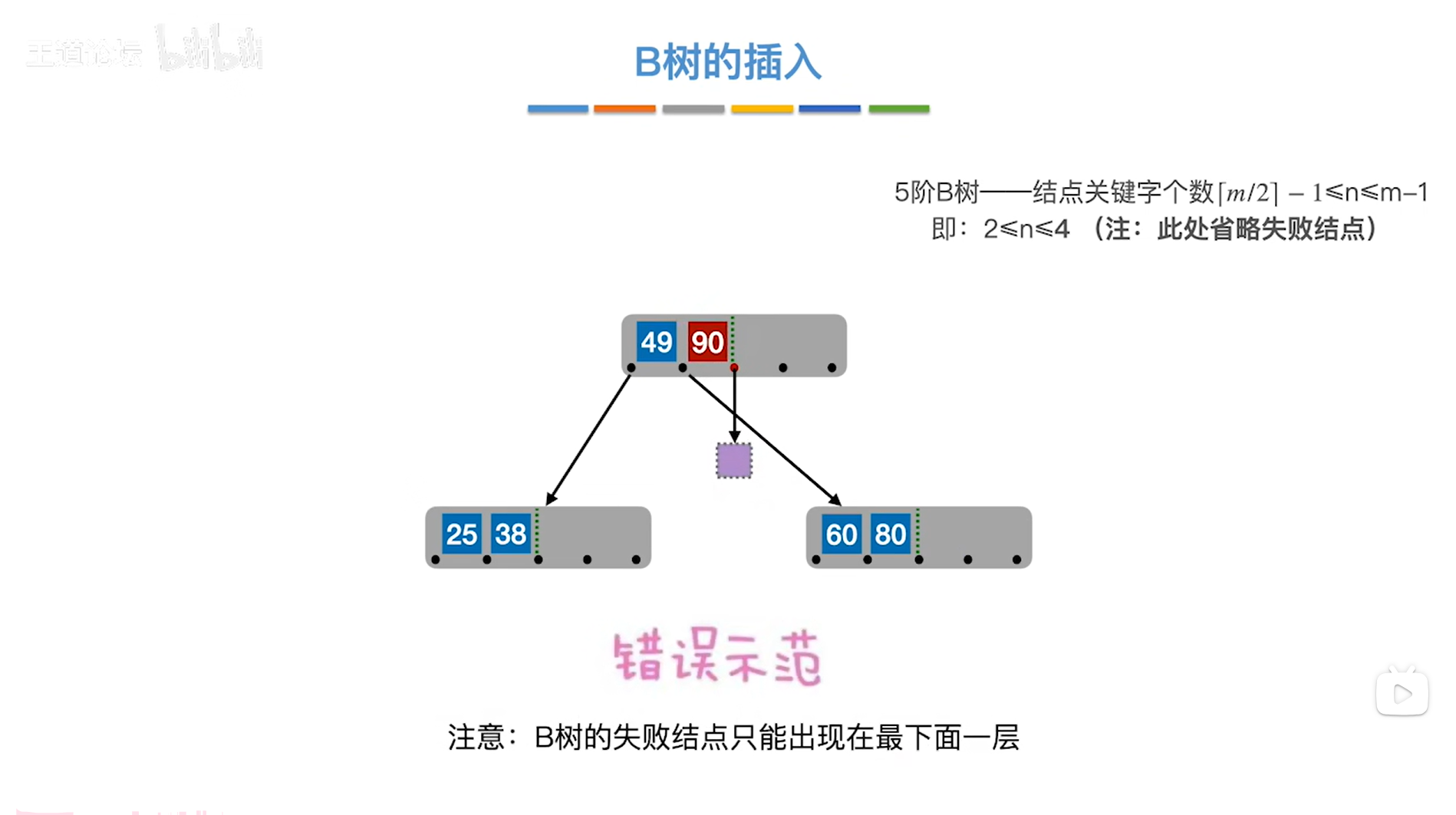
如上图,
接下来插入关键字99,
需要注意的是每一次新插入的元素一定是插入到最底层的终端结点中,用"查找"规则来确定插入位置(详情见"7.11.B树"),
从根结点出发,由于关键字99大于49,且49的右边已经没有关键字了,所以99要插在49的右孩子指针所指的子树中,
49的右孩子指针所指的子树中根结点包含的关键字为60、80、90,该结点内的关键字个数没有达到上限,所以可以继续插入关键字,接下来检查该结点内的关键字,
第一个关键字60比99更小,所以会检查下一个关键字80,
第二个关键字80比99更小,所以会检查下一个关键字90,
第三个关键字90比99更小,又因为90后已经没有关键字了,所以99应插在90的后面,
如下图:
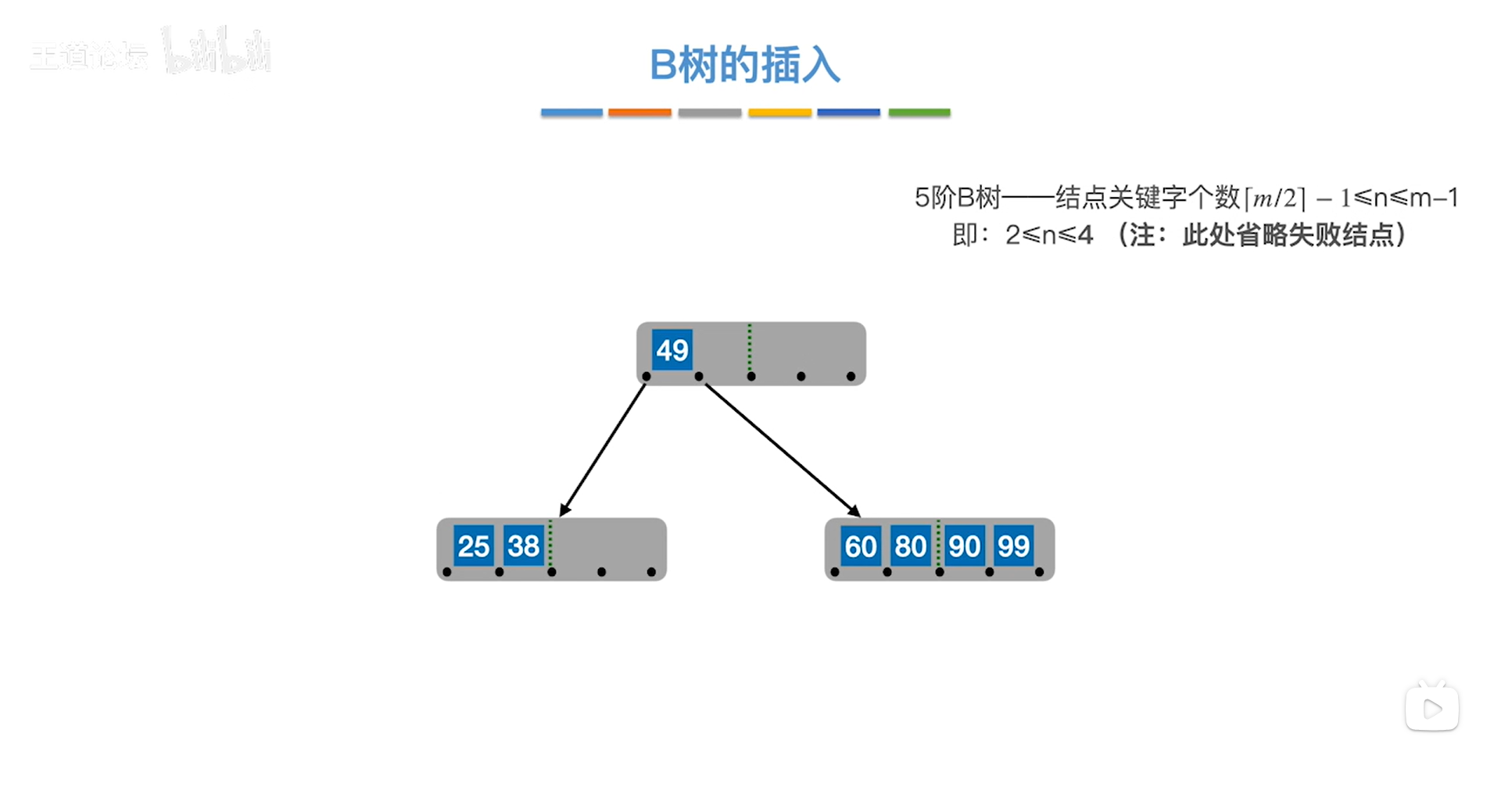
如上图,
接下来插入关键字88,
需要注意的是每一次新插入的元素一定是插入到最底层的终端结点中,用"查找"规则来确定插入位置(详情见"7.11.B树"),
从根结点出发,由于关键字88大于49,且49的右边已经没有关键字了,所以88要插在49的右孩子指针所指的子树中,
49的右孩子指针所指的子树中根结点包含的关键字为60、80、90、99,该结点内的关键字个数已经达到上限,所以如果继续插入关键字,就必须在新的结点内插入,但首先需要检查该结点内的关键字,
第一个关键字60比88更小,所以会检查下一个关键字80,
第二个关键字80比88更小,所以会检查下一个关键字90,
第三个关键字90比88更大,所以88应插在80和90之间,
如下图:
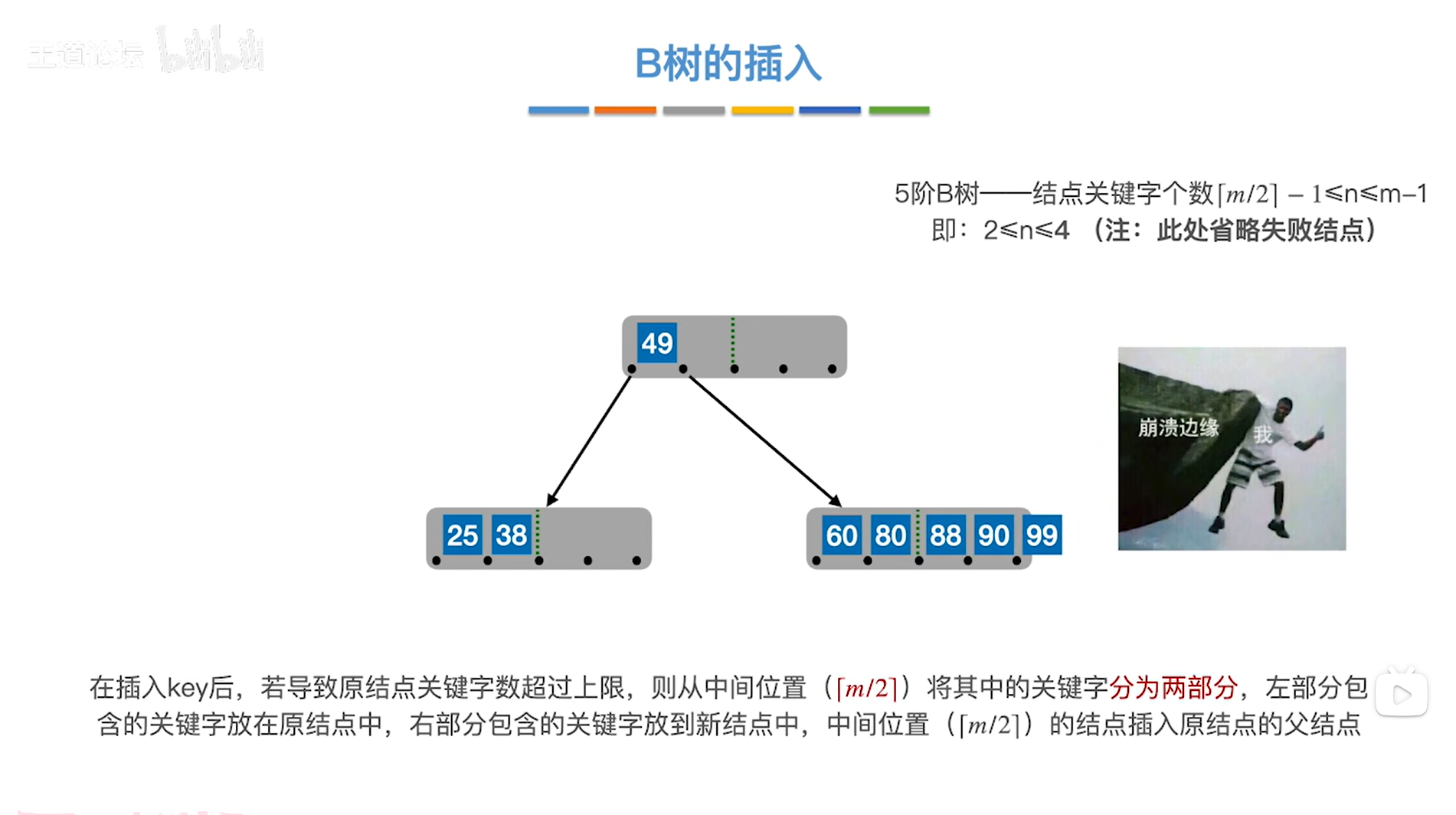
如上图,
注:此时是5阶B树
当前处理的结点中包含了关键字60、80、88、90、99,关键字个数为5个,已经超出了上限,
所以要把中间位置⌈m/2⌉=⌈5/2⌉=3索引上的元素88提到其父结点中,然后把88左、右两个部分的元素分别放到两个不同的结点中,
元素88右边的元素都比88大,所以把元素88右边的元素都连到元素88右边的指针中,这么做刚好也保证了"左<中<右"的特性(元素88左边的元素同理),
如下图:
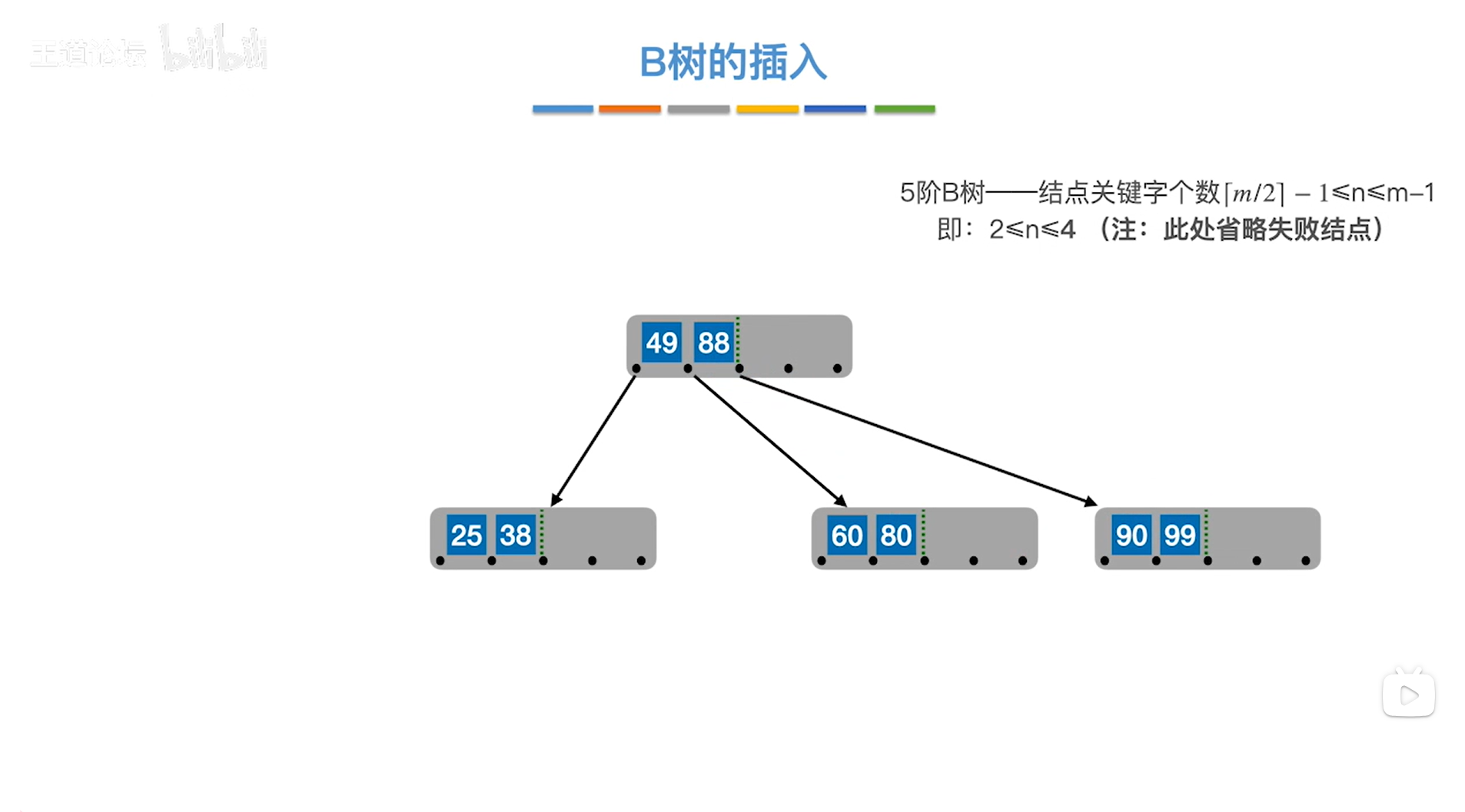
如上图,
接下来插入关键字83,
需要注意的是每一次新插入的元素一定是插入到最底层的终端结点中,用"查找"规则来确定插入位置(详情见"7.11.B树"),
从根结点出发,根结点包含的关键字为49,88,接下来检查该结点内的关键字,
第一个关键字49比83更小,所以会检查下一个关键字88,
第二个关键字88比83更大,所以83应插在49和88之间,
因此接下来要检查包含关键字60、80的结点,该结点内的关键字个数没有达到上限,所以可以继续插入关键字,接下来检查该结点内的关键字,
第一个关键字60比83更小,所以会检查下一个关键字80,
第二个关键字80比83更小,又因为80后已经没有关键字了,所以83应插在80的后面,
如下图:
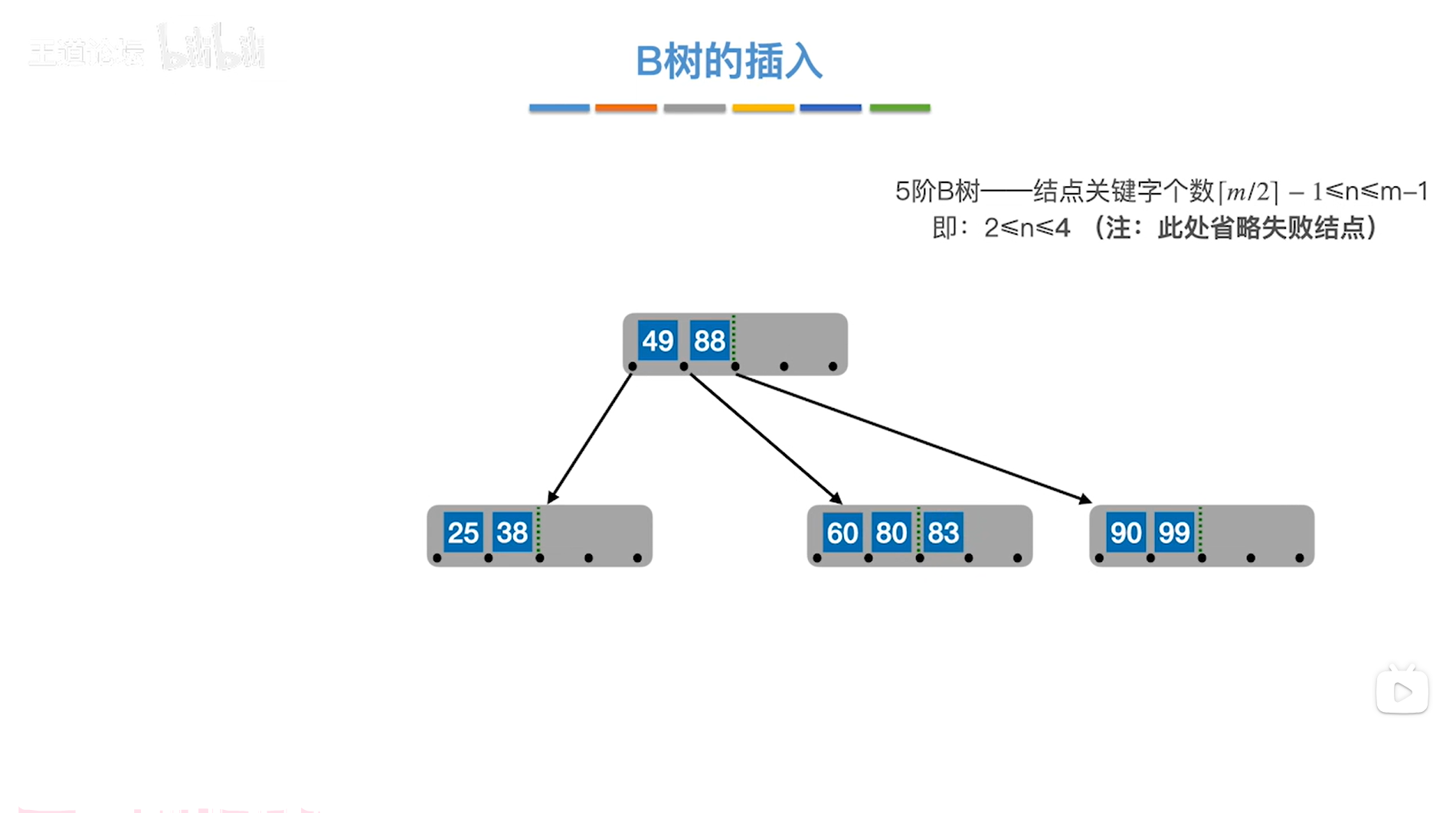
如上图,
接下来插入关键字87,原理同上,
如下图:
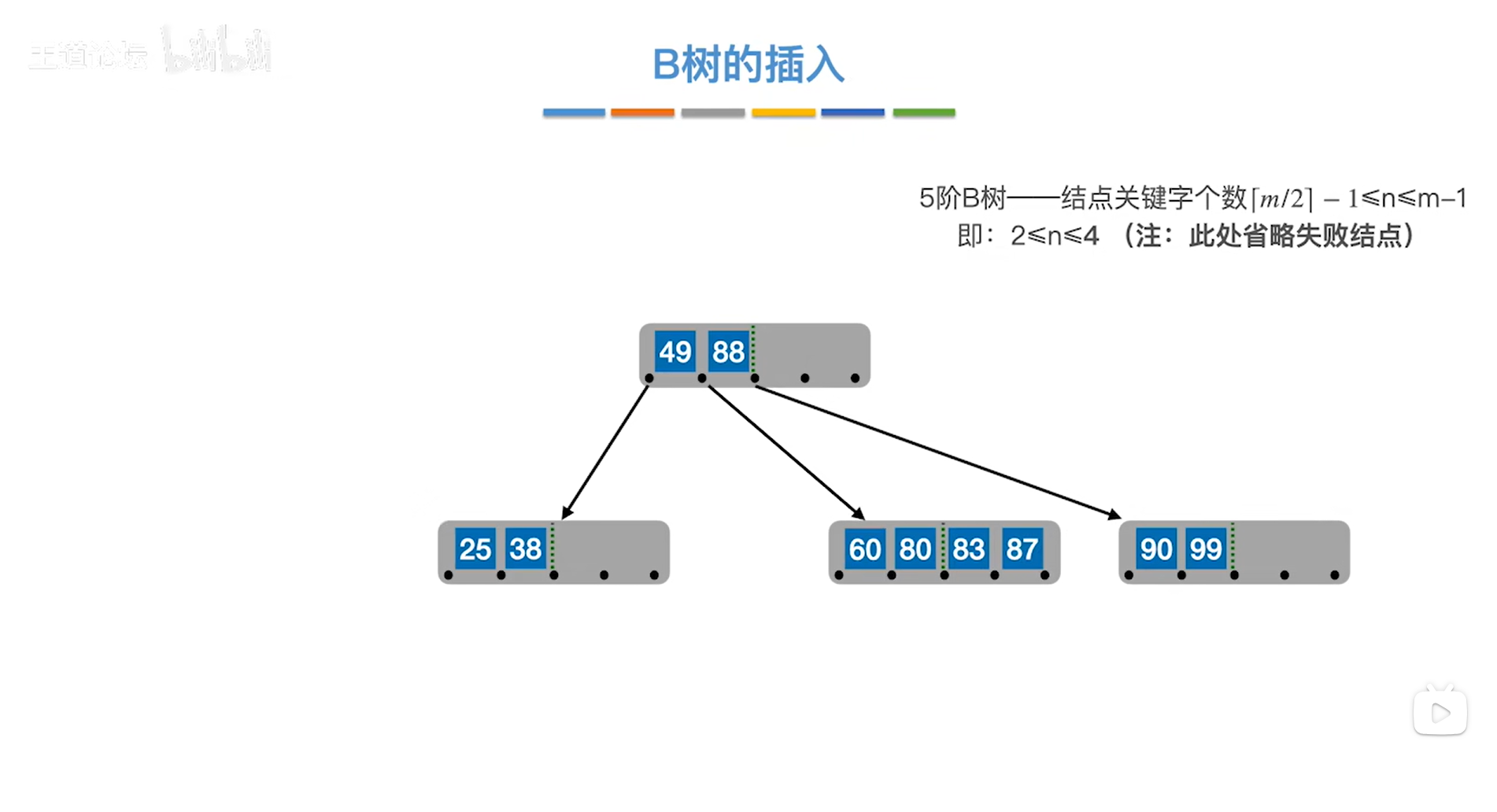
如上图,
接下来插入关键字70,原理同上,
70应插在60和80之间,
如下图:
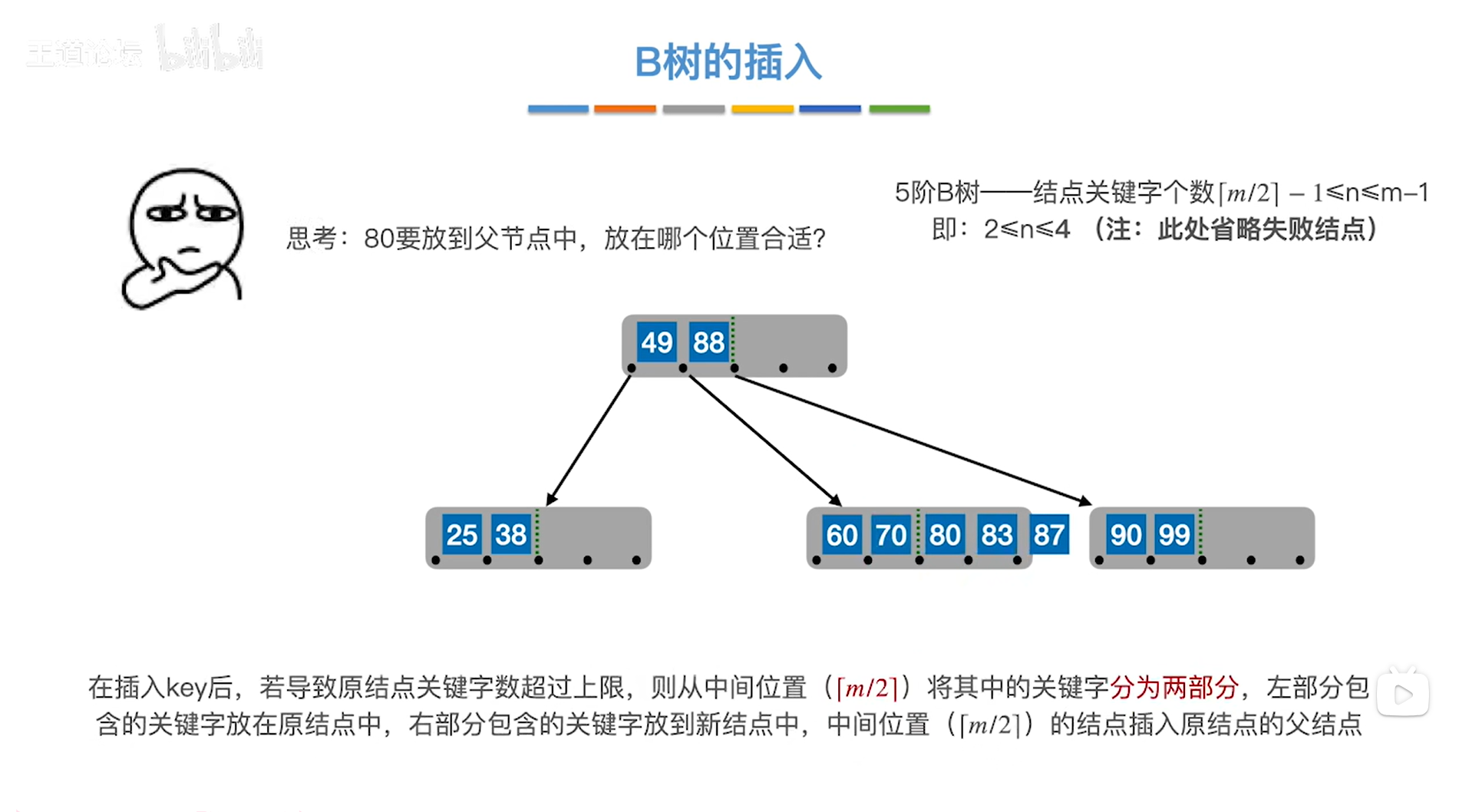
如上图,
注:此时是5阶B树
当前处理的结点中包含了关键字60、70、80、83、87,关键字个数为5个,已经超出了上限,
所以要把中间位置⌈m/2⌉=⌈5/2⌉=3索引上的元素80提到其父结点中,然后把80左、右两个部分的元素分别放到两个不同的结点中,
现在要思考的问题是:元素80应该放到其父结点的哪个位置呢?显然,把元素80放到其父结点中应保证其父结点中的元素依然是有序排放的,所以80应放到49和88中间,
如下图:
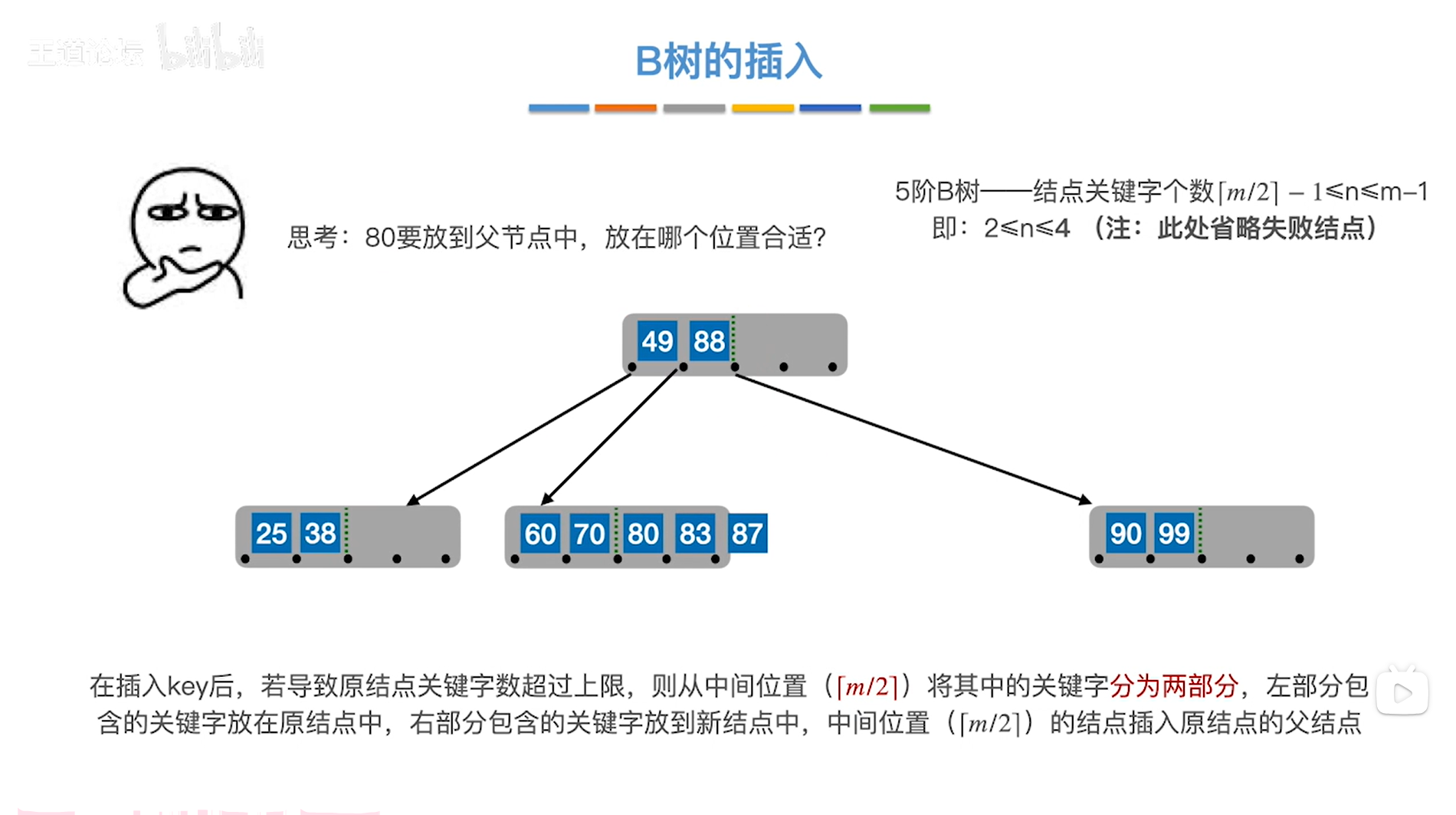
如上图,
总结:如果一个关键字因分裂需要把它提到父结点中,那么就应该把这个关键字放到指向它所属的结点的这条指针所对应的这个点的右边的位置。
接下来依次插入关键字92、93、94,
如下图:
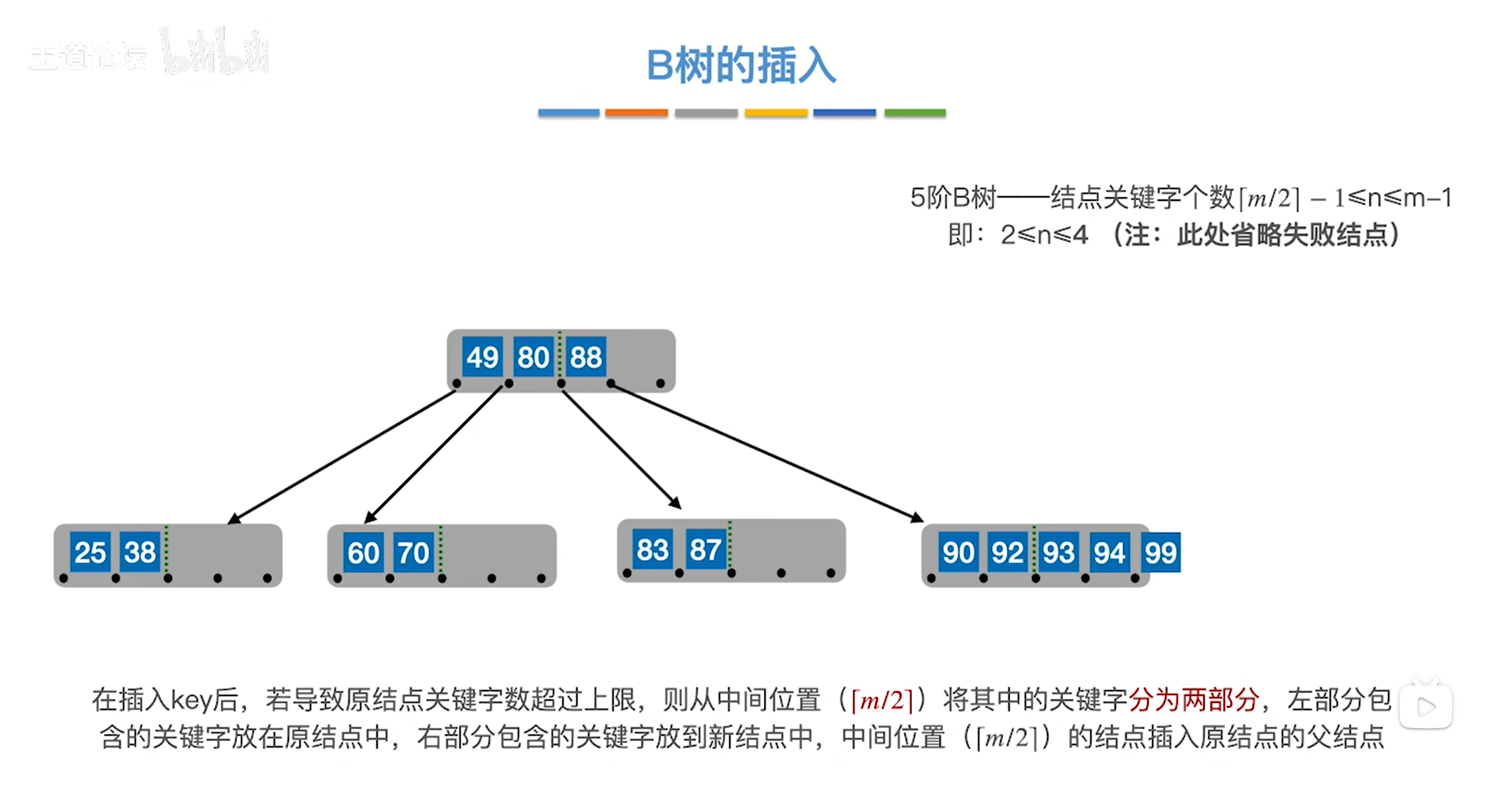
如上图,
注:此时是5阶B树
当前处理的结点中包含了关键字90、92、93、94、99,关键字个数为5个,已经超出了上限,
所以要把中间位置⌈m/2⌉=⌈5/2⌉=3索引上的元素93提到其父结点中,然后把93左、右两个部分的元素分别放到两个不同的结点中,
现在要思考的问题是:元素93应该放到其父结点的哪个位置呢?显然,把元素93放到其父结点中应保证其父结点中的元素依然是有序排放的,所以93应放到88的后面,
还需要把93右边的元素所组成的新结点连到93的右指针上
如下图:
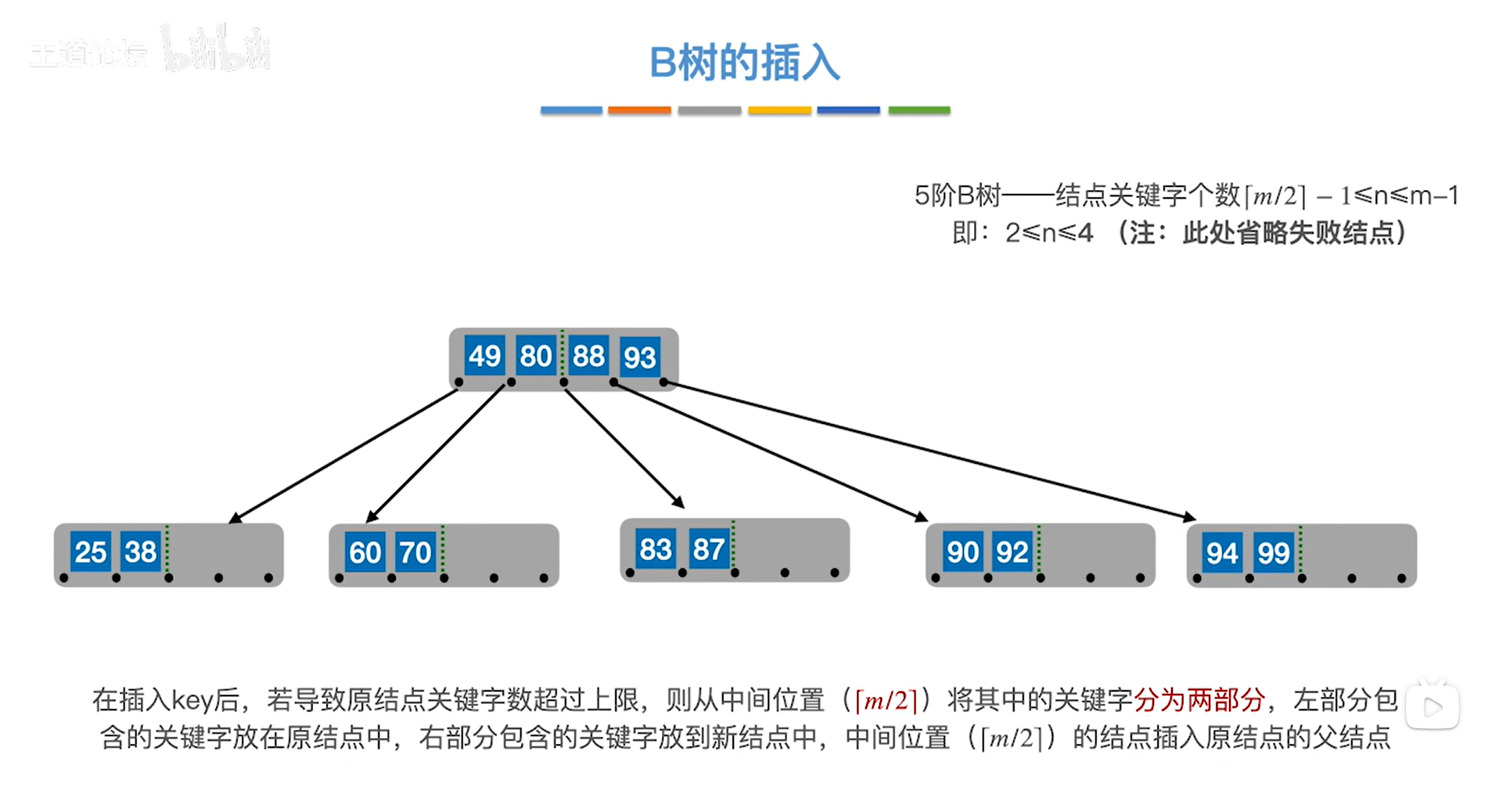
如上图,
接下来依次插入关键字73、74、75,
如下图:
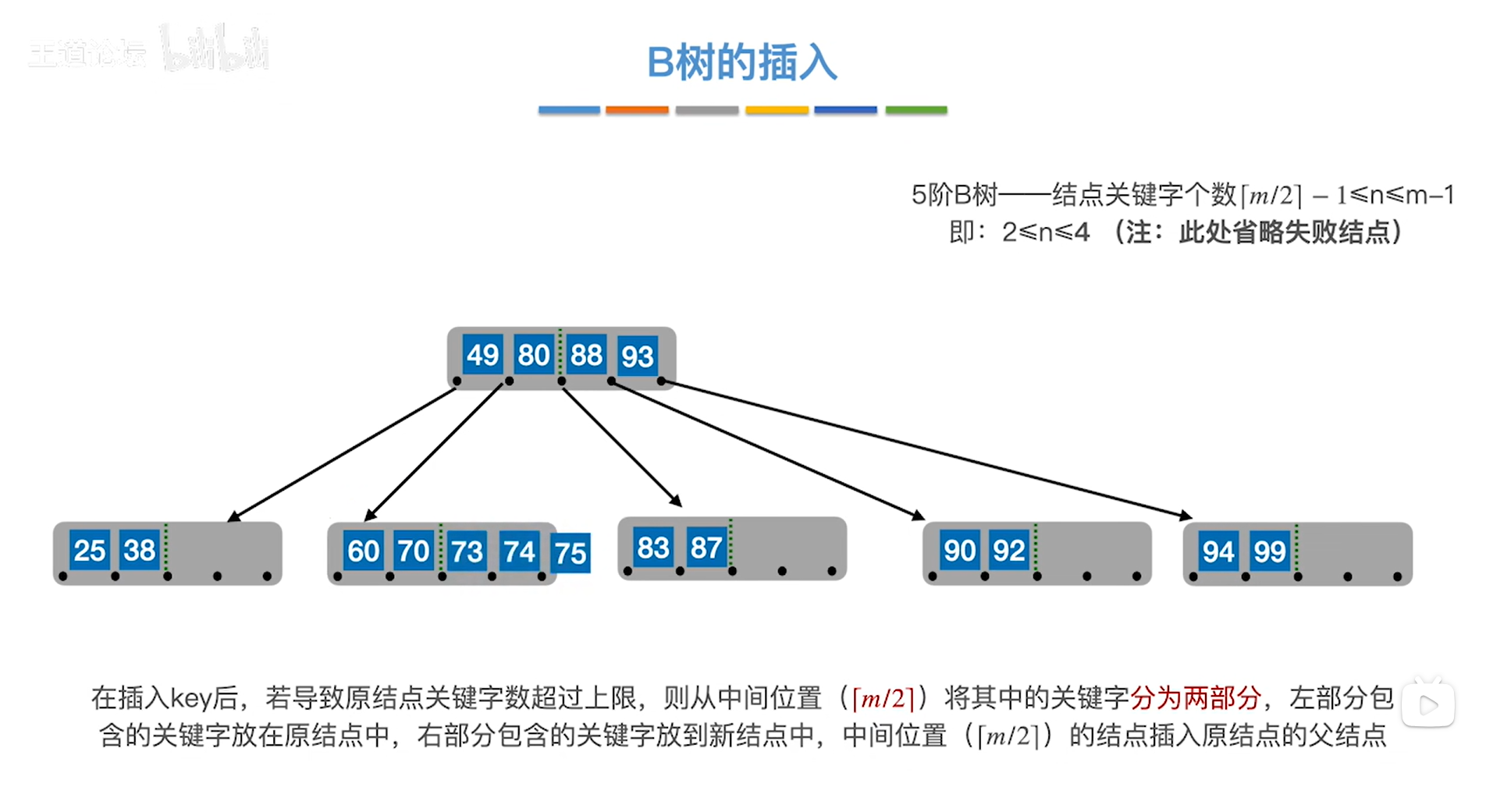
如上图,
注:此时是5阶B树
当前处理的结点中包含了关键字60、70、73、74、75,关键字个数为5个,已经超出了上限,
所以要把中间位置⌈m/2⌉=⌈5/2⌉=3索引上的元素73提到其父结点中,然后把73左、右两个部分的元素分别放到两个不同的结点中,
现在要思考的问题是:元素73应该放到其父结点的哪个位置呢?显然,把元素73放到其父结点中应保证其父结点中的元素依然是有序排放的,所以73应放到49和80中间,
还需要把73右边的元素所组成的新结点连到73的右指针上
如下图:
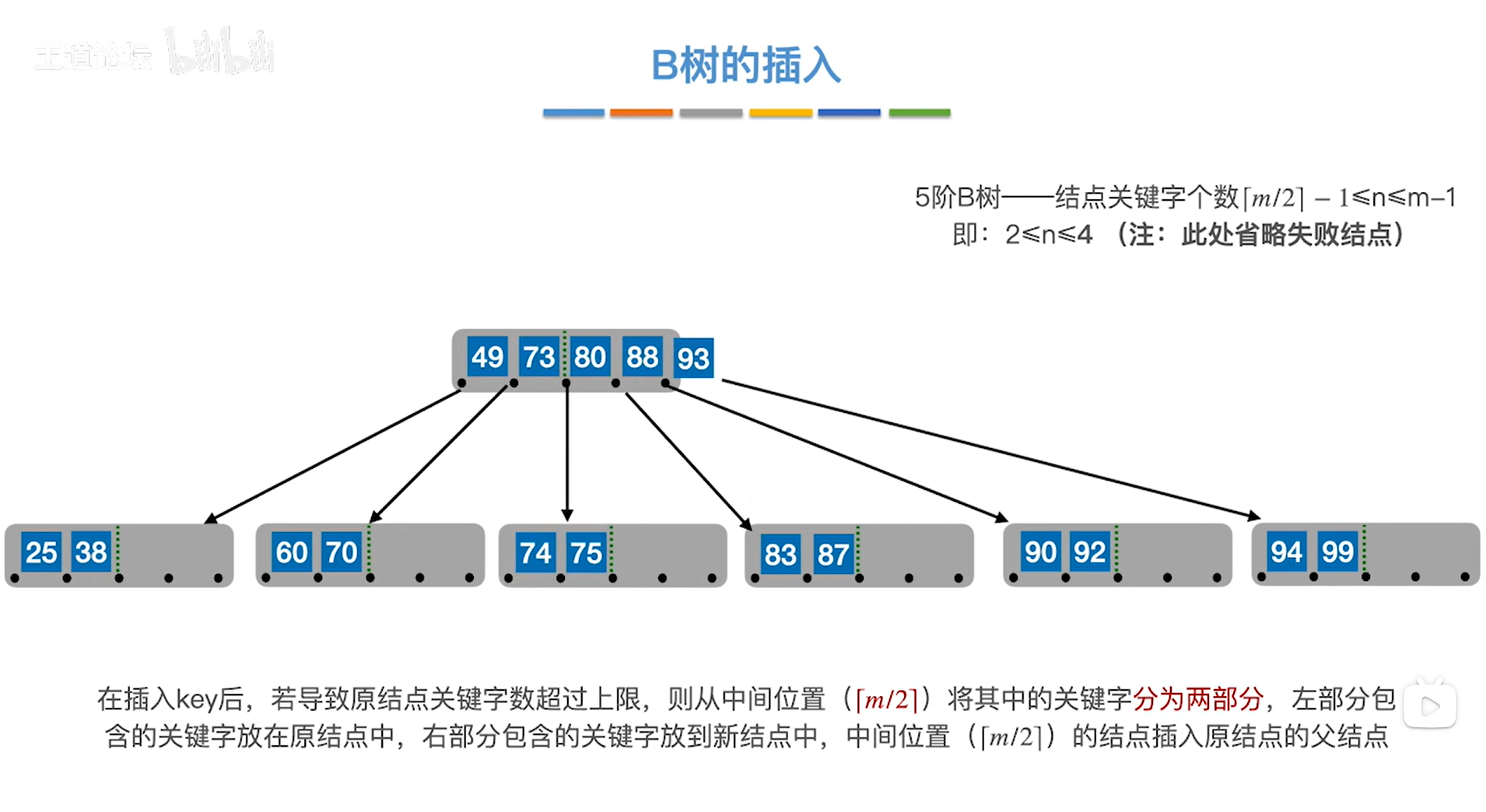
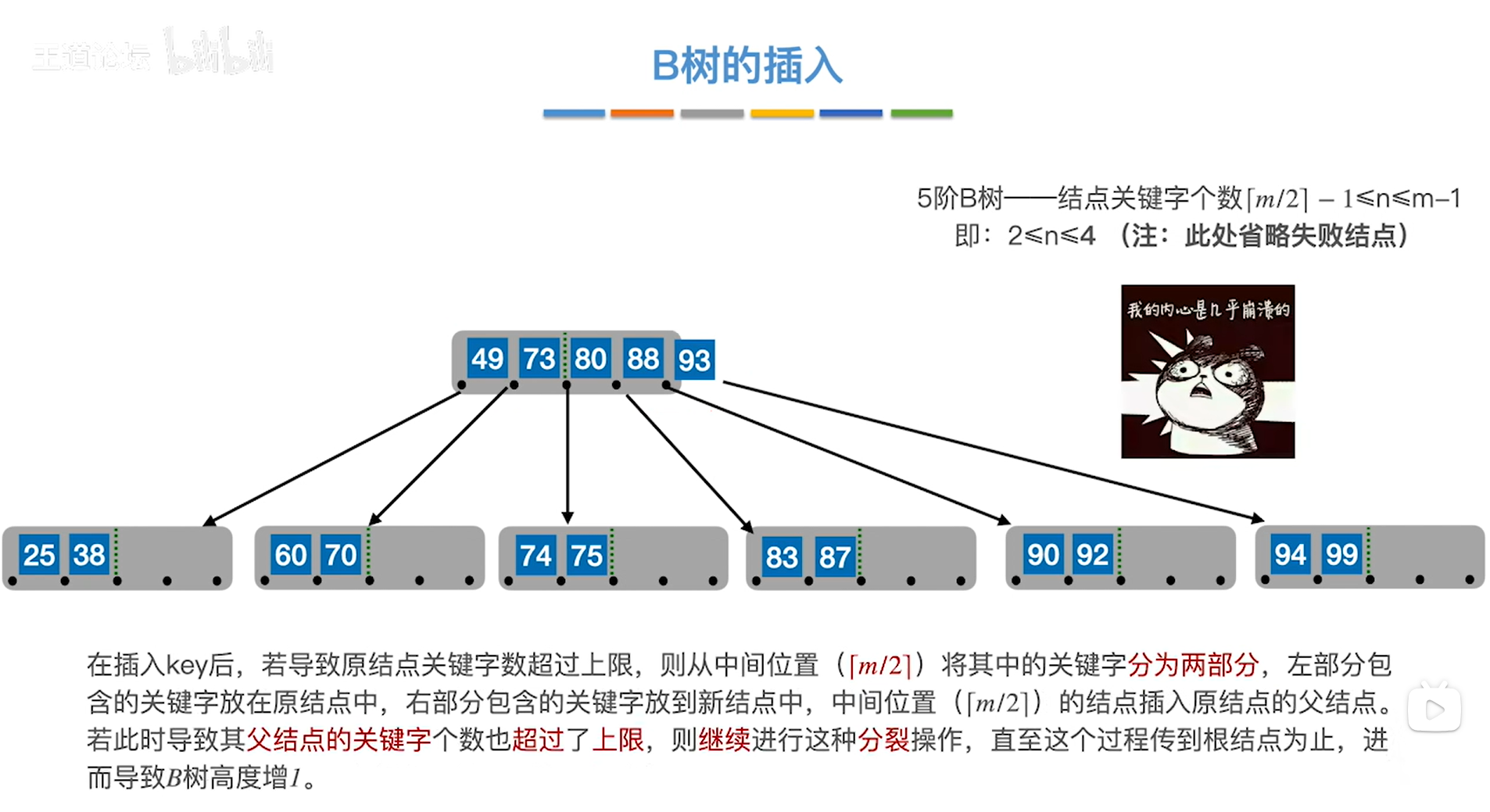
如上图,
注:此时是5阶B树
此时整棵树的根结点中包含了关键字49、73、80、88、93,关键字个数为5个,已经超出了上限,
整棵树的根结点不存在父结点,那么这种情况该如何处理呢?需要把整棵树的根结点继续向上分裂,这种情况下分裂的方法与之前类似,
所以要把中间位置⌈m/2⌉=⌈5/2⌉=3索引上的元素80提到其父结点中,由于现在整棵树的根结点没有父结点,所以会新建立一个结点作为根结点的父结点,然后把80放到该父结点中,最后把80的左、右两个部分连在父结点的左、右两边,
如下图:
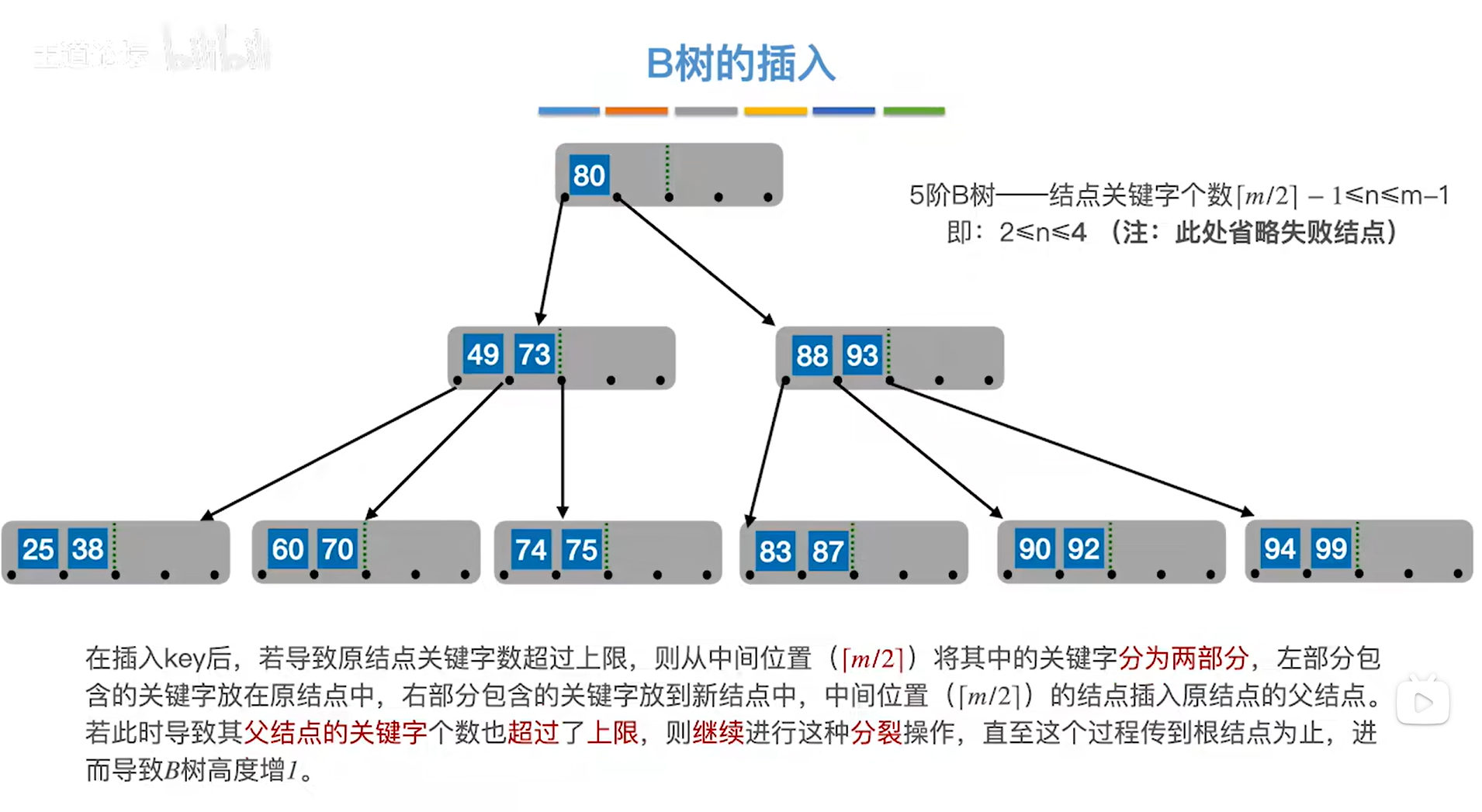
如上图,
此时满足了5阶B树的特性与要求,根结点中允许只有1个关键字,除了根结点、叶子结点外的结点中关键字至少2个、至多4个。
2.总结:

二.B树的删除:
1.实例:
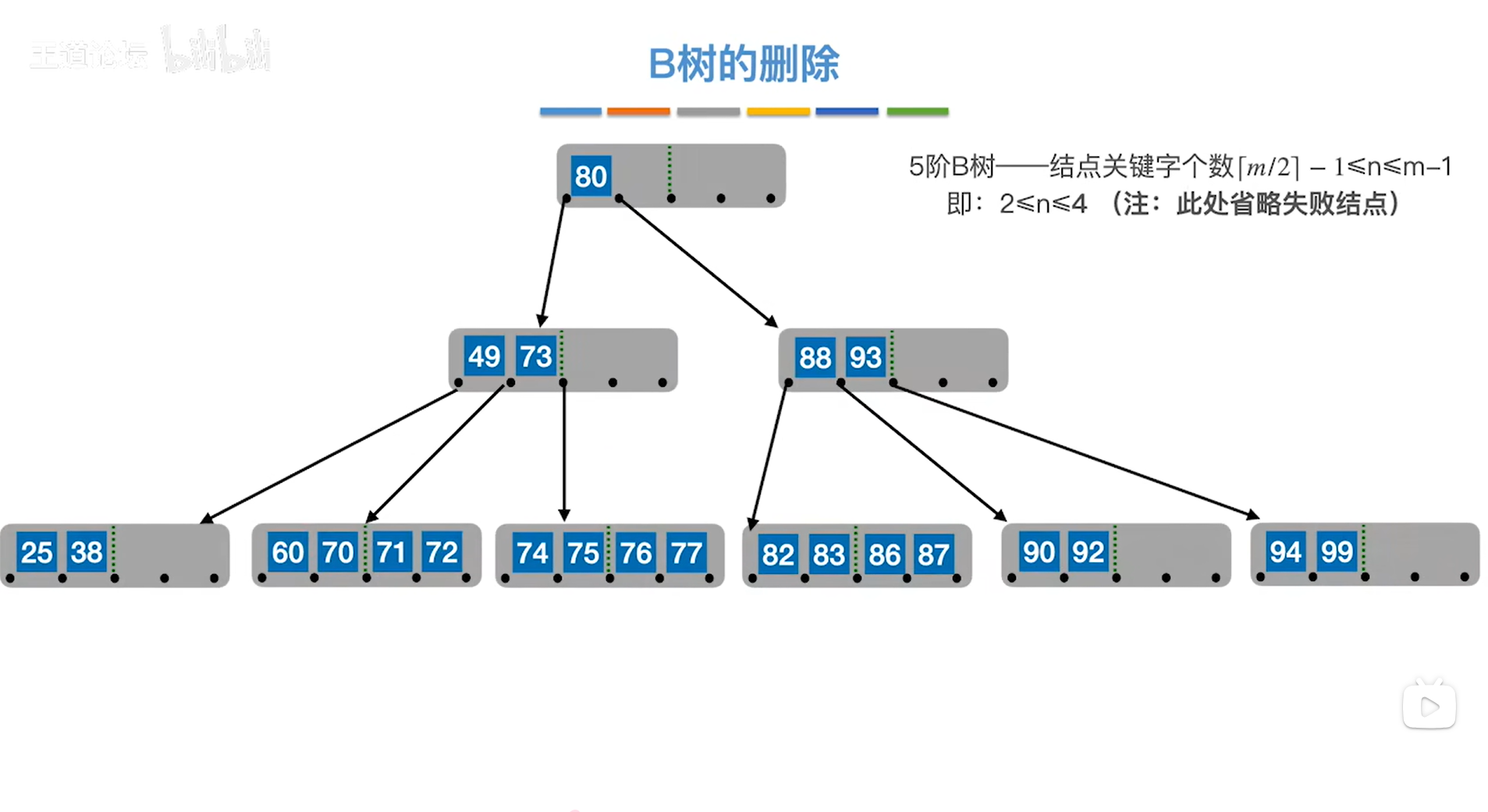
以上述图片的5阶B树为例,
首先删除关键字60,由于60位于终端结点,所以直接删除即可,
并且删除60之后,当前所操作的结点的关键字个数为3
并没有低于5阶B树所要求的下限2,
如下图:
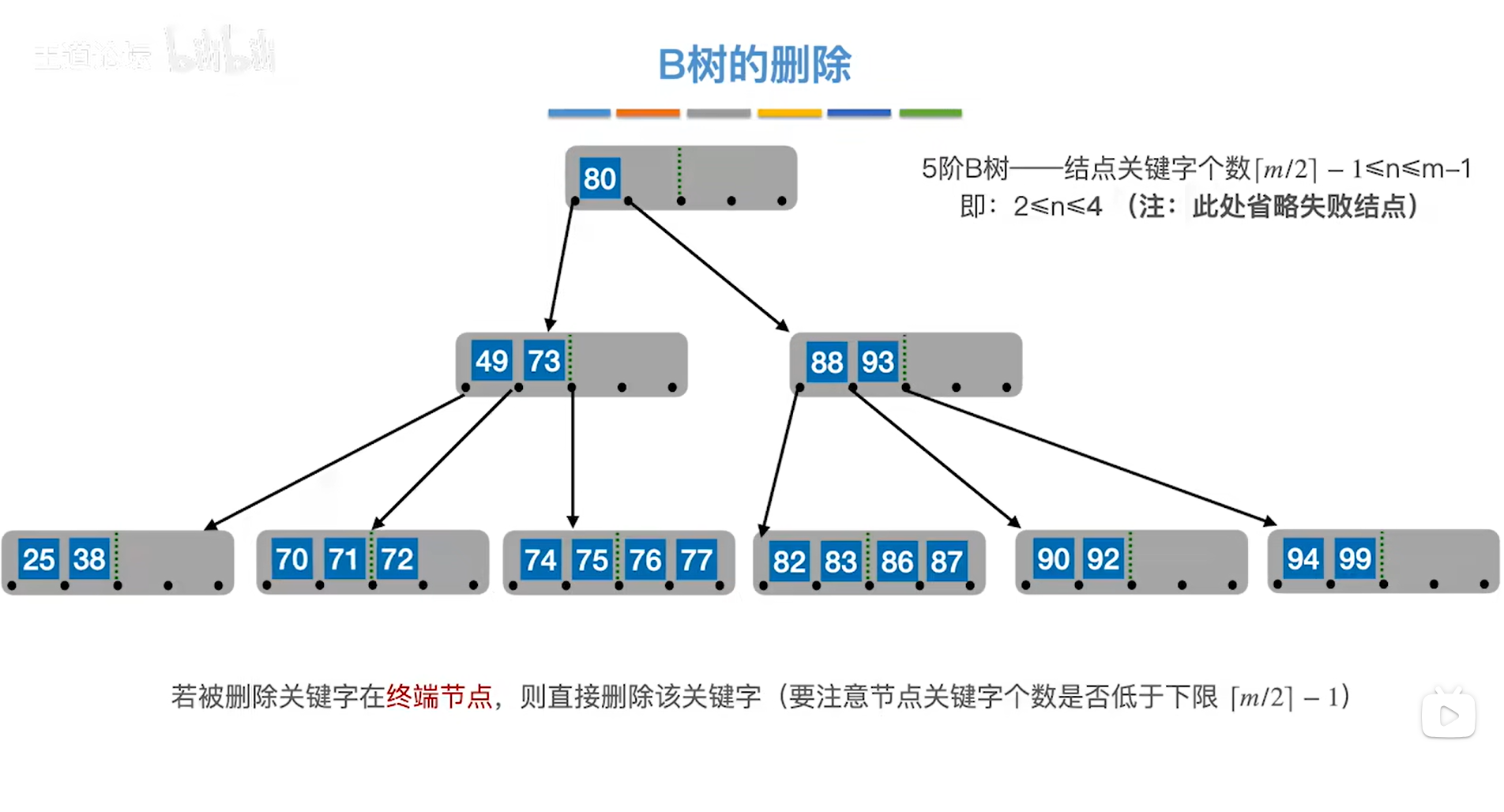
如上图,
接下来删除关键字80,80位于非终端结点中,且80删除之后根结点就不存在了,
之后该怎么做呢?可以找到80的直接前驱或直接后继来顶替80的位置,
先看用80的直接前驱来顶替80的位置,80的直接前驱是77(找直接前驱的方法详情见"5.11.在线索二叉树中找前驱和后继"),
如下图:
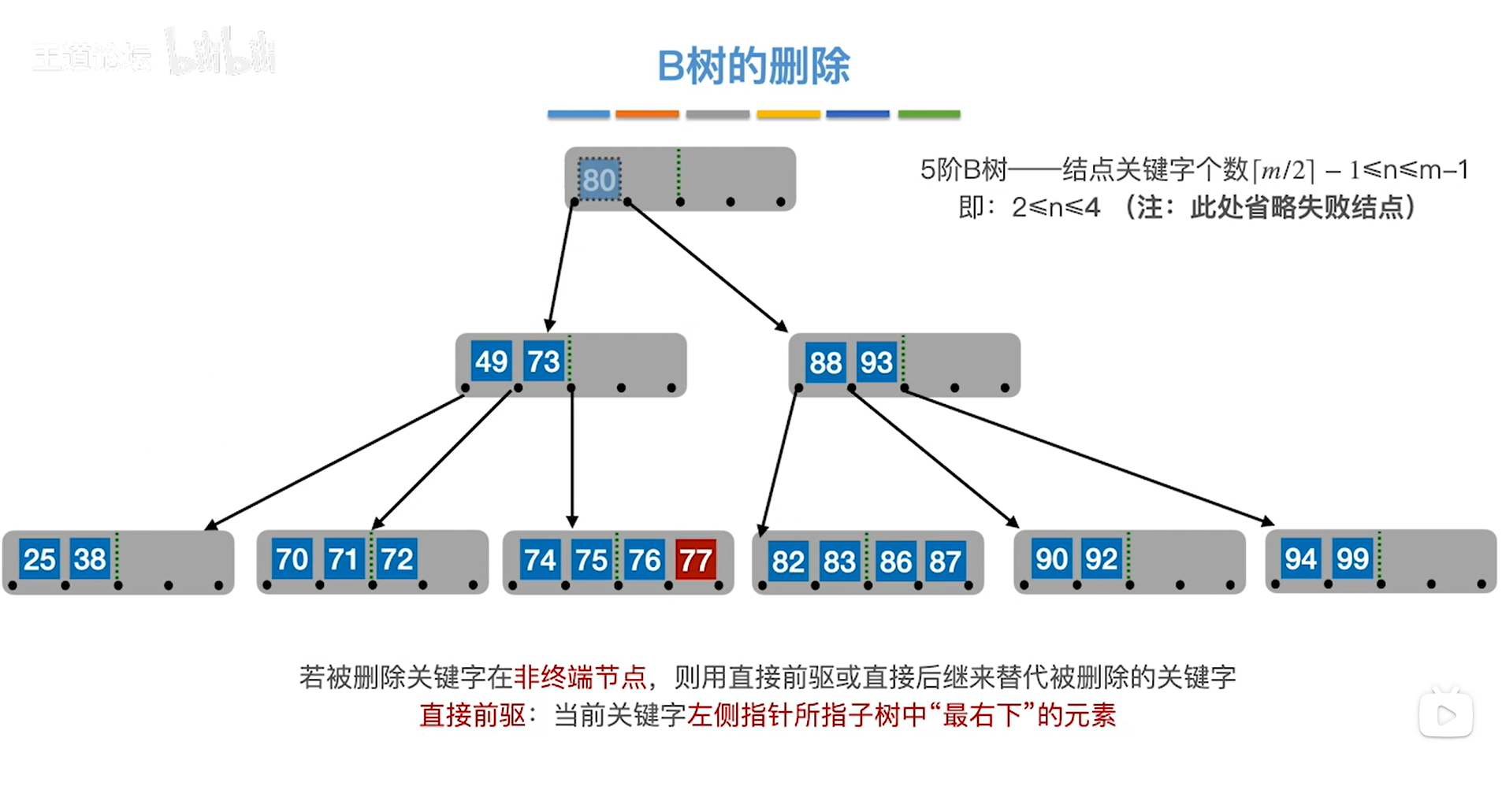
如上图,
现在用关键字77顶替80的位置,
如下图:
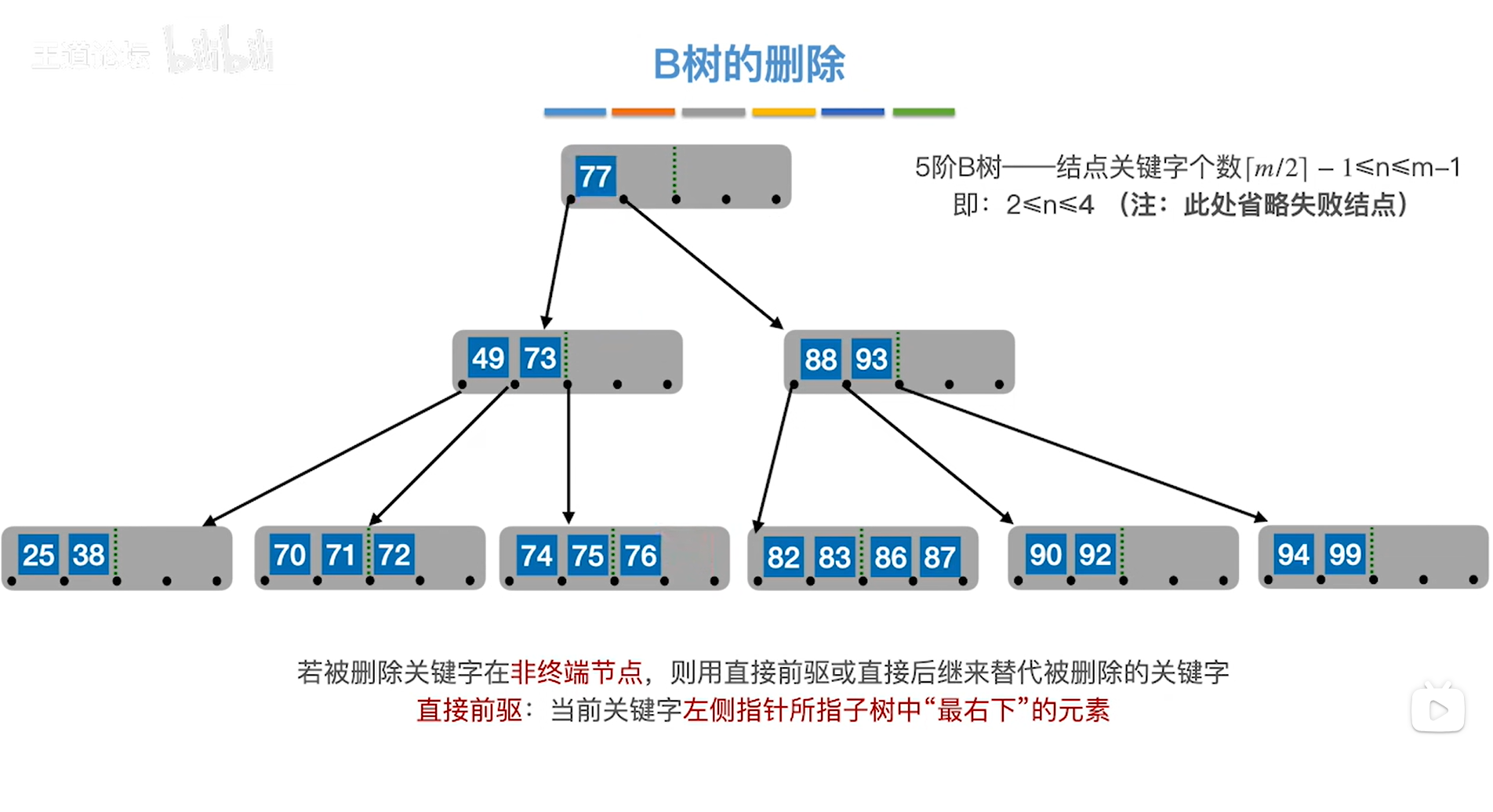
如上图,
刚才的操作相当于把非终端结点的删除操作转换成对终端结点的删除操作,这是用直接前驱来替代。
接下来删除关键字77,77位于非终端结点中,且77删除之后根结点就不存在了,
因此可以用77的直接后继来顶替77的位置,77的直接后继是82(找直接前驱的方法详情见"5.11.在线索二叉树中找前驱和后继"),
如下图:
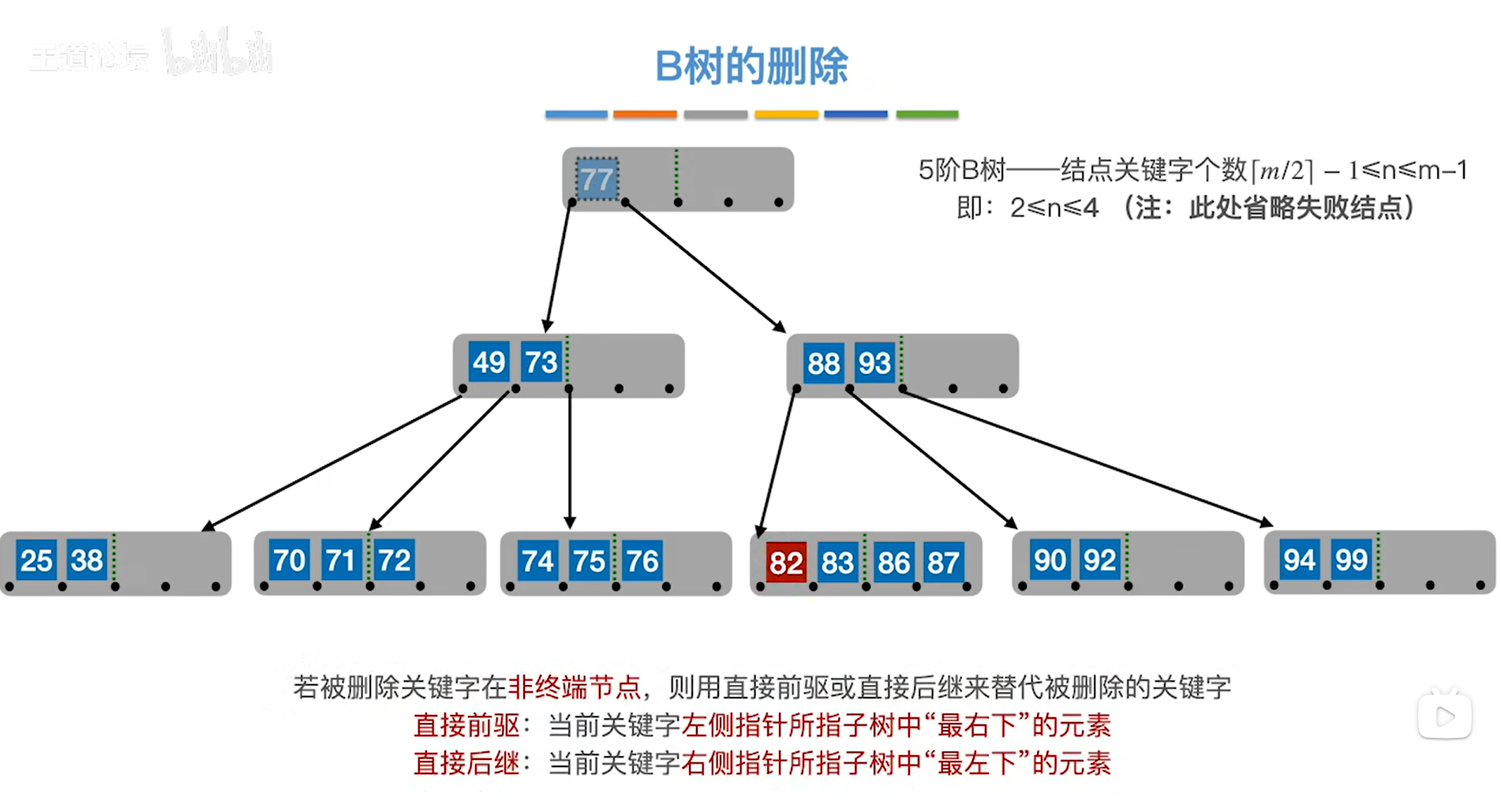
如上图,
现在用关键字82顶替77的位置,
关键字82移动后需要把82原来所在的结点里的关键字进行调整使其有序,
如下图:
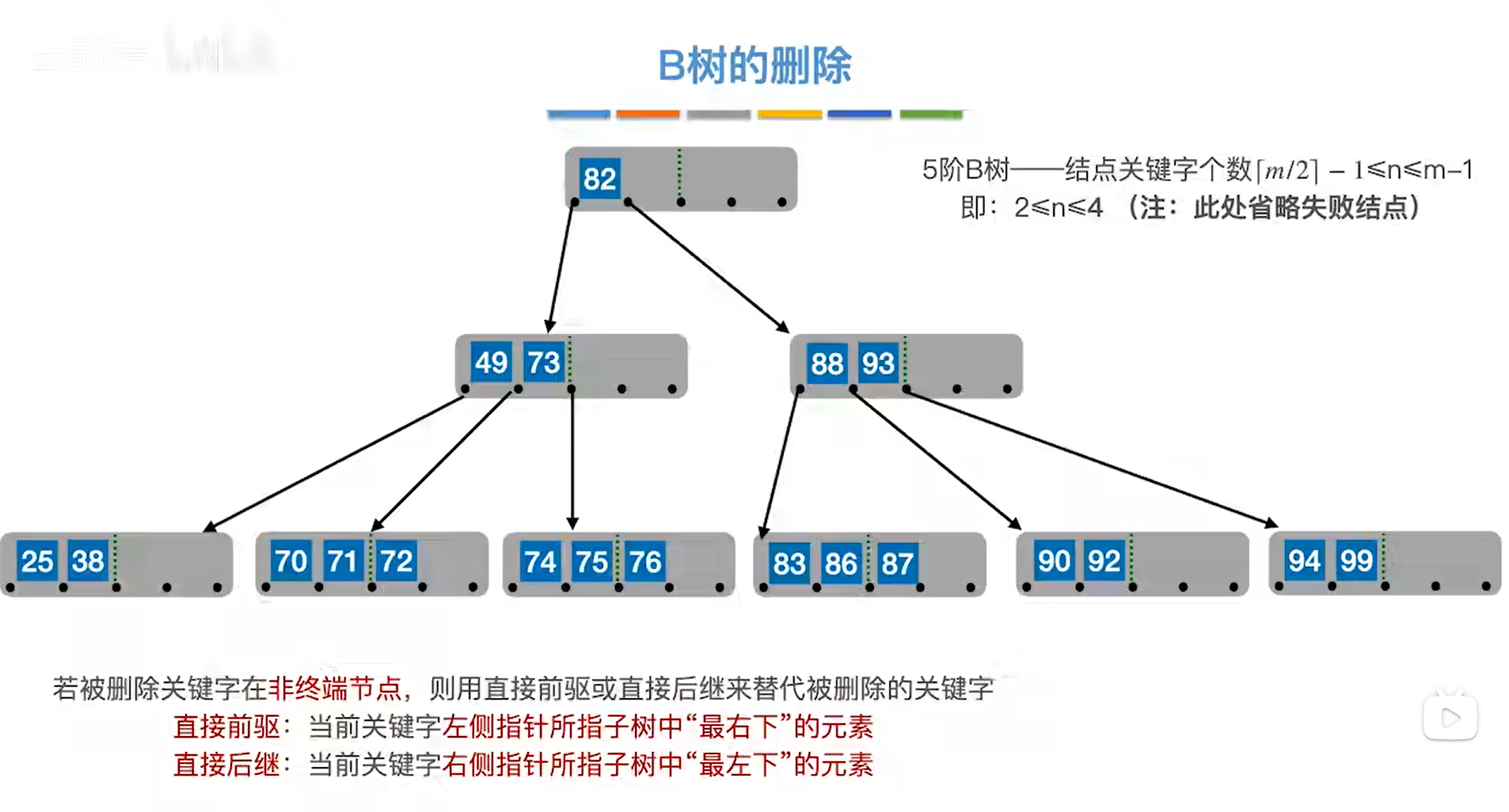
如上图,
注:所找到的"直接前驱"或"直接后继"一定位于终端结点,所以对非终端结点的删除操作一定可以转化为对终端结点的删除操作,
如下图:
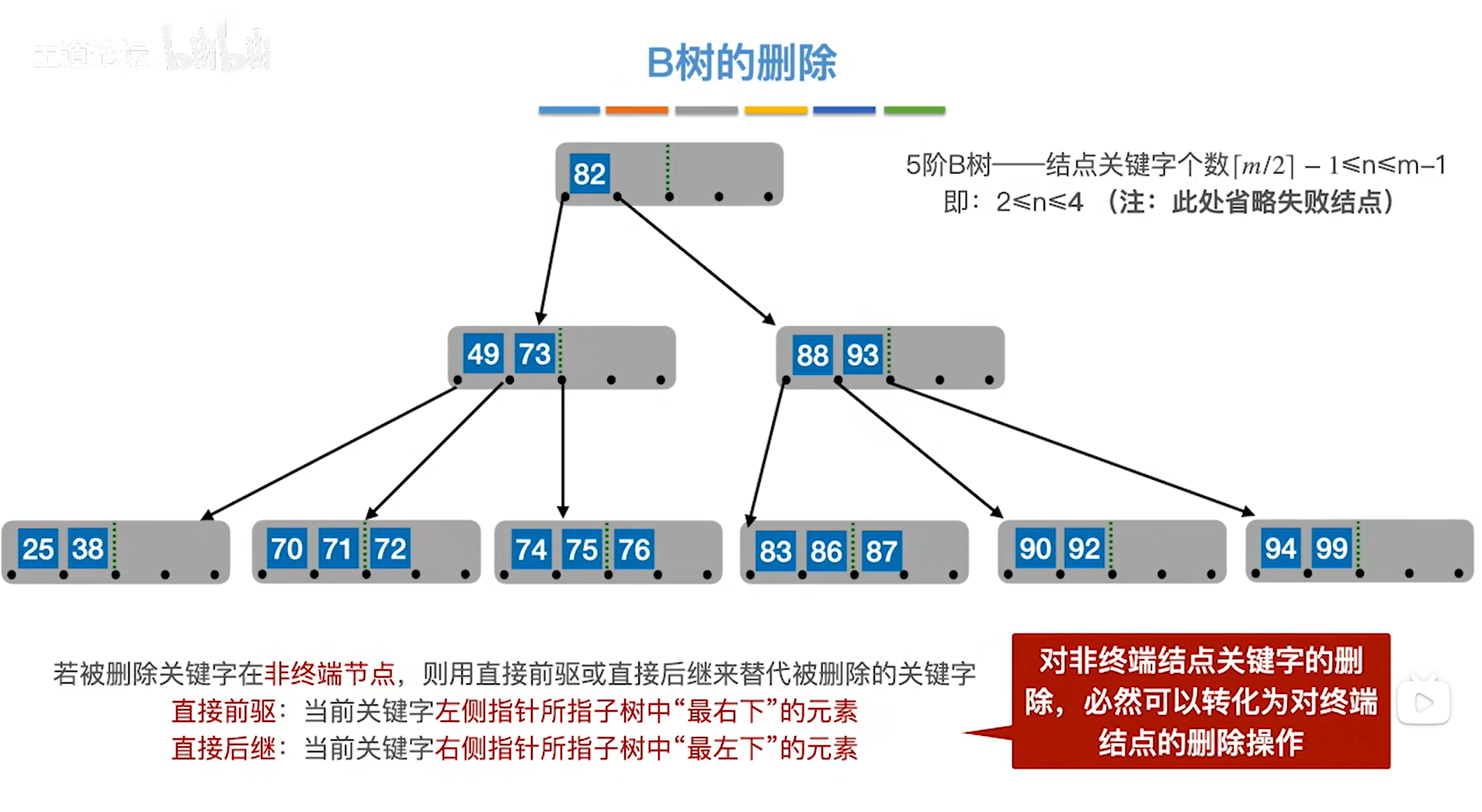
如上图,
接下来删除关键字38,
如下图:
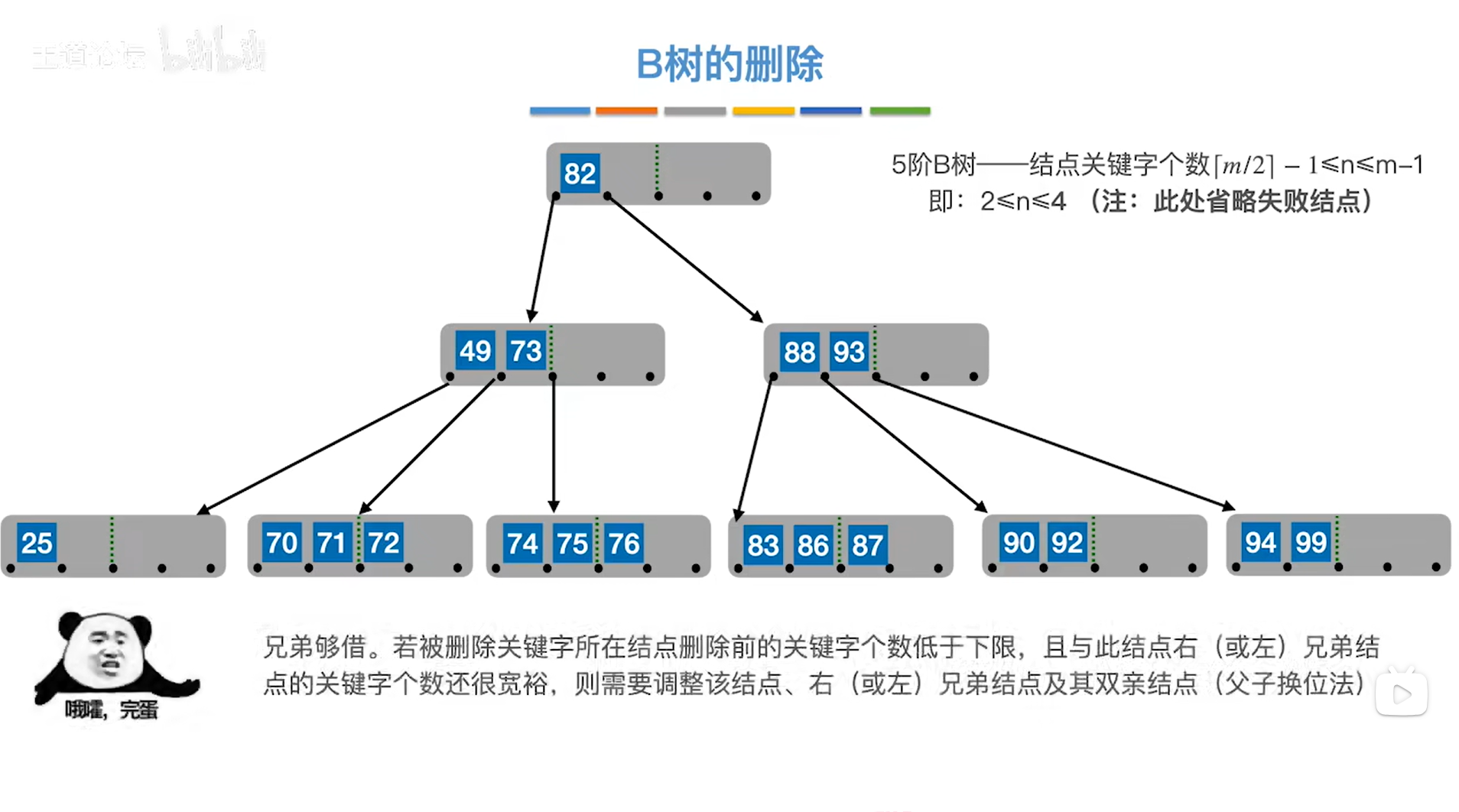
如上图,
删除38之后,38原来所在的结点中只有1个关键字25,低于1个结点中关键字个数的下限2,
这时该如何处理呢?这个需要分多种情况来讨论->
情况一:"兄弟够借"->意思是当前结点的关键字个数如果低于下限,但是它的兄弟结点里的关键字个数是足够的,比如38原来所在的结点的右兄弟结点的关键字个数绰绰有余,所以可以把这个右兄弟结点中的关键字贡献出一个,比如把关键字70贡献出来,但这显然不对,因为在其上方的父结点中包含关键字49,49的左子树里的关键字都必须要小于49,所以如果把70贡献出来,就不满足B树的特性(同理其他的关键字也无法贡献出来),
如下图:
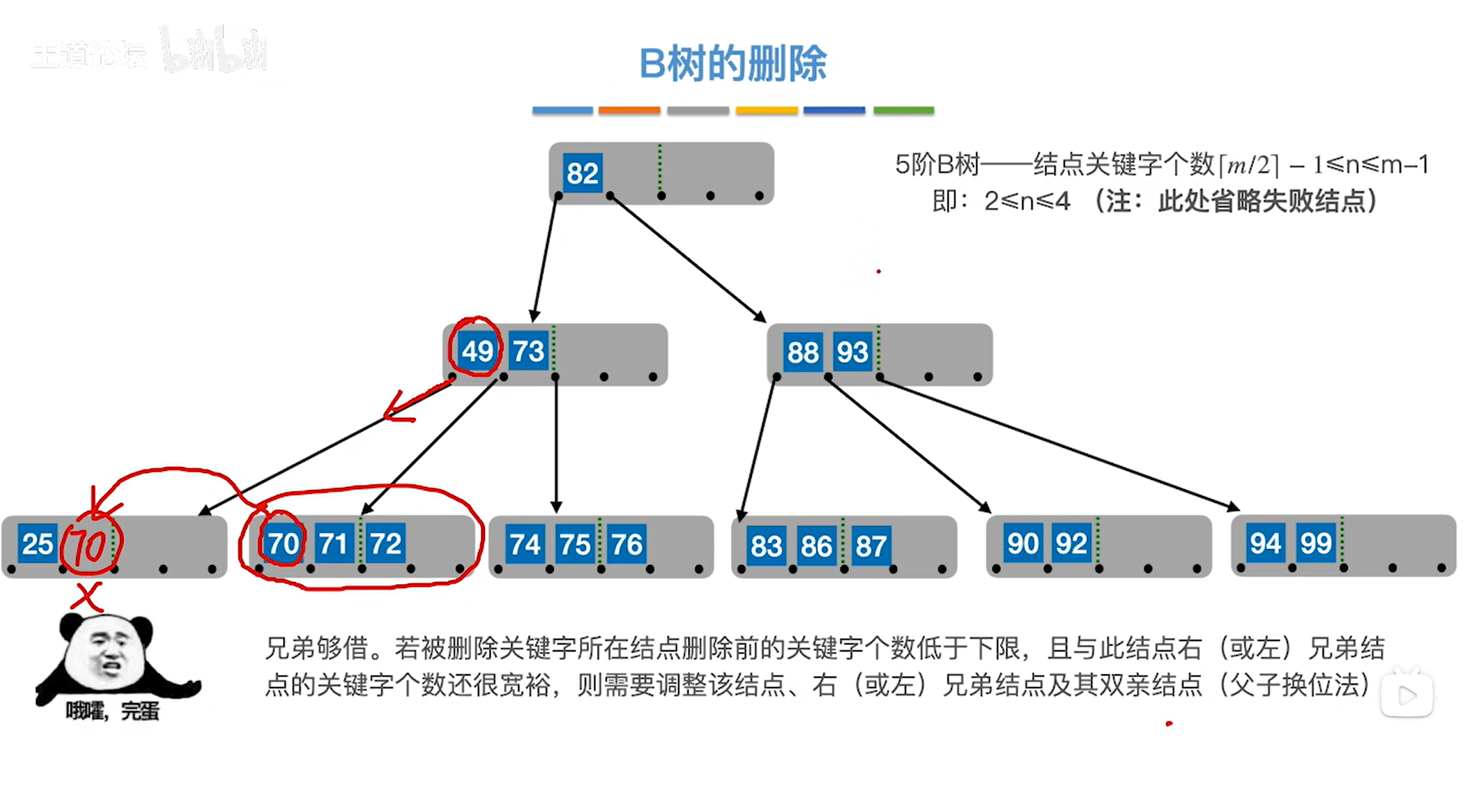
如上图,
那应该怎么解决呢?
注:结点中关键字是递增排序的
只包含关键字25的结点中,25的后继就是指向25的结点的指针中右边的第一个关键字49,
25后继的后继即关键字49的后继,49的后继就是49右子树里最小的关键字70,
因此首先可以把关键字49放入包含关键字25的结点中,然后让关键字70顶替49的位置,这样就可以保证B树的特性,70的左子树中的所有关键字都比70小,70的右子树中的所有关键字都比70大,
所以刚才这种情况可以概述为"当右兄弟很宽裕时,会找到当前结点的后继结点、后继的后继结点来填补空缺",
如下图:
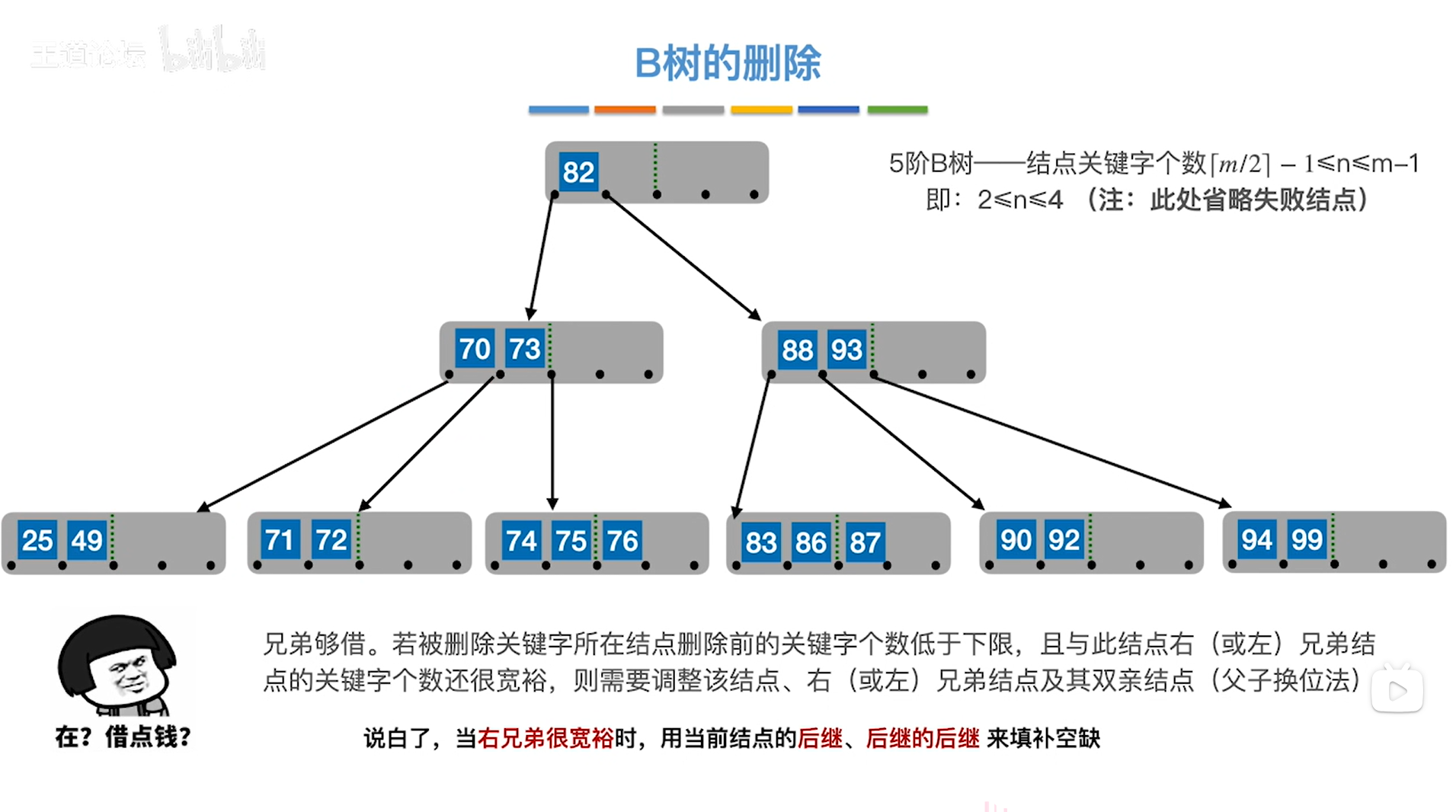
如上图,
接下来删除关键字90,
如下图:
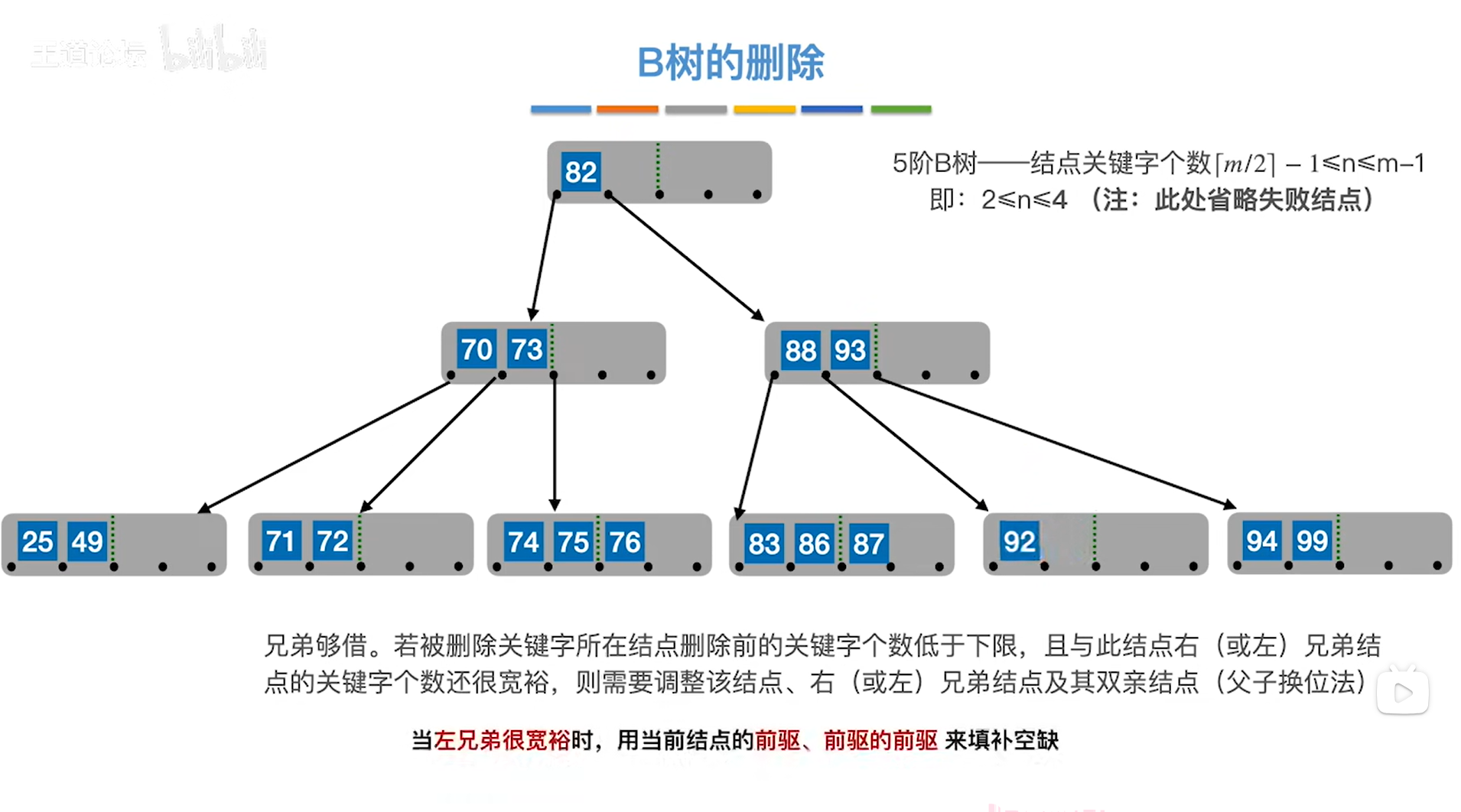
如上图,
删除90之后,90原来所在的结点中只有1个关键字92,低于1个结点中关键字个数的下限2,
那应该怎么解决呢?
注:结点中关键字是递增排序的
如果让只有1个关键字92的结点的右兄弟结点贡献一个关键字的话,该右兄弟结点中关键字的个数就会低于2,不符合5阶B树的特性,
但只有1个关键字92的结点的左兄弟结点显然关键字是绰绰有余的,所以可以向左兄弟借,
所以这种情况可以概述为"当左兄弟很宽裕时,会找到当前结点的前驱关键字、前驱的前驱关键字来填补空缺",
只包含关键字92的结点中,92的前驱就是指向92的结点指针左边的关键字88,
92前驱的前驱即关键字88的前驱,88的前驱就是88左子树中最大的关键字87,
接下来就是把88插入到92的前面,然后用87顶替88的位置,
此时就保证了5阶B树的特性,
如下图:
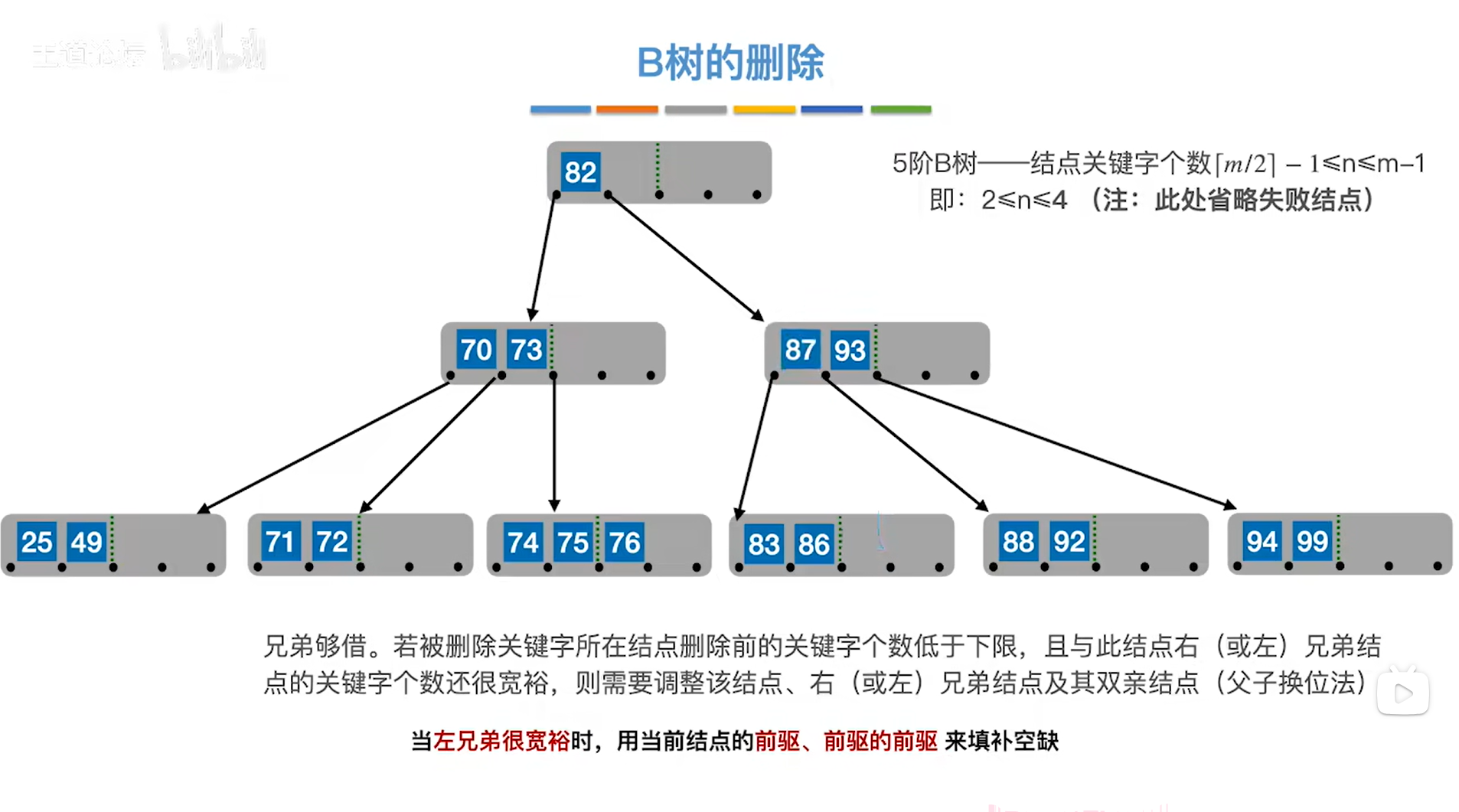
如上图,
总之,删除操作必须要始终保持B树的特性,
如下图:
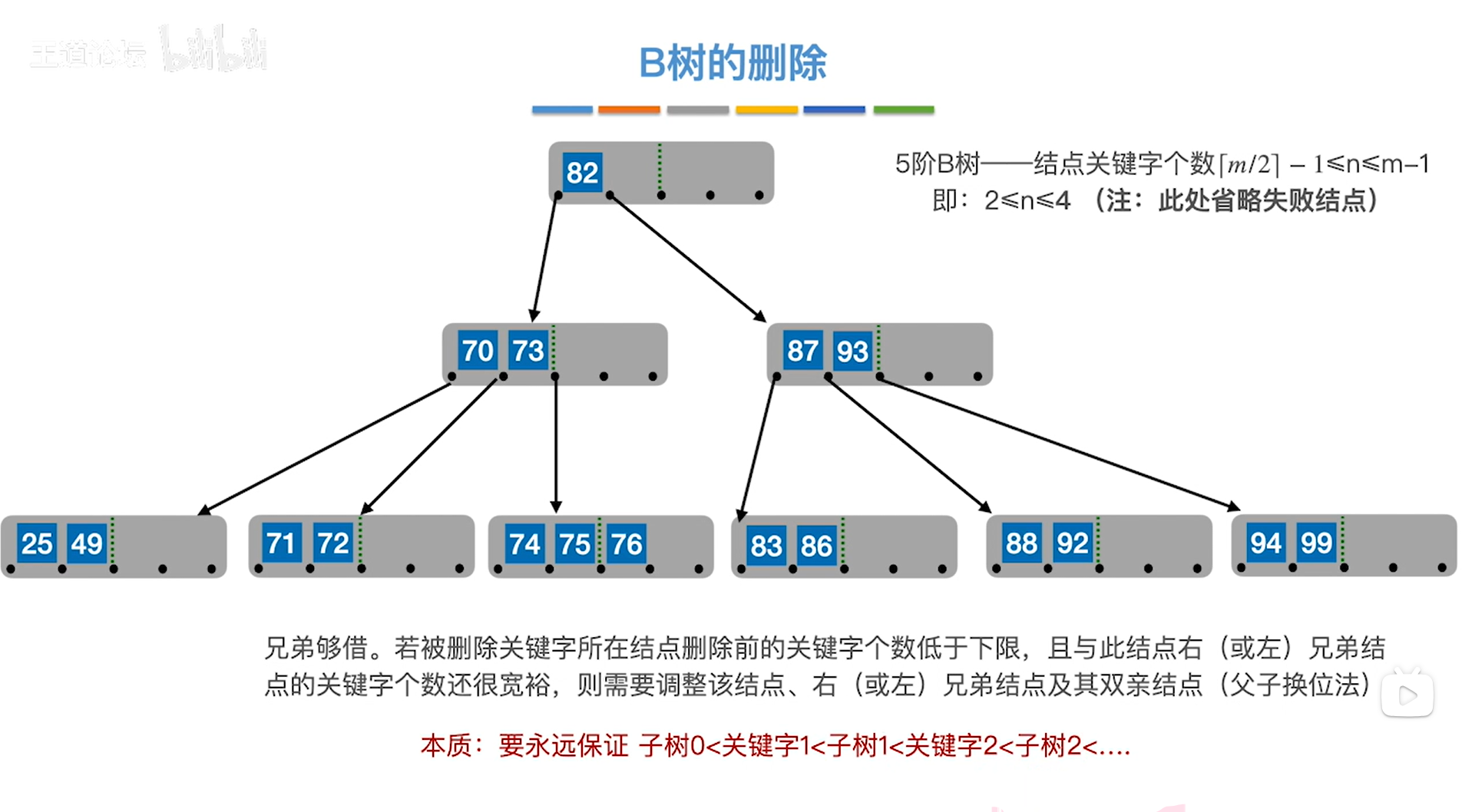
如上图,
接下来删除关键字49,
如下图:
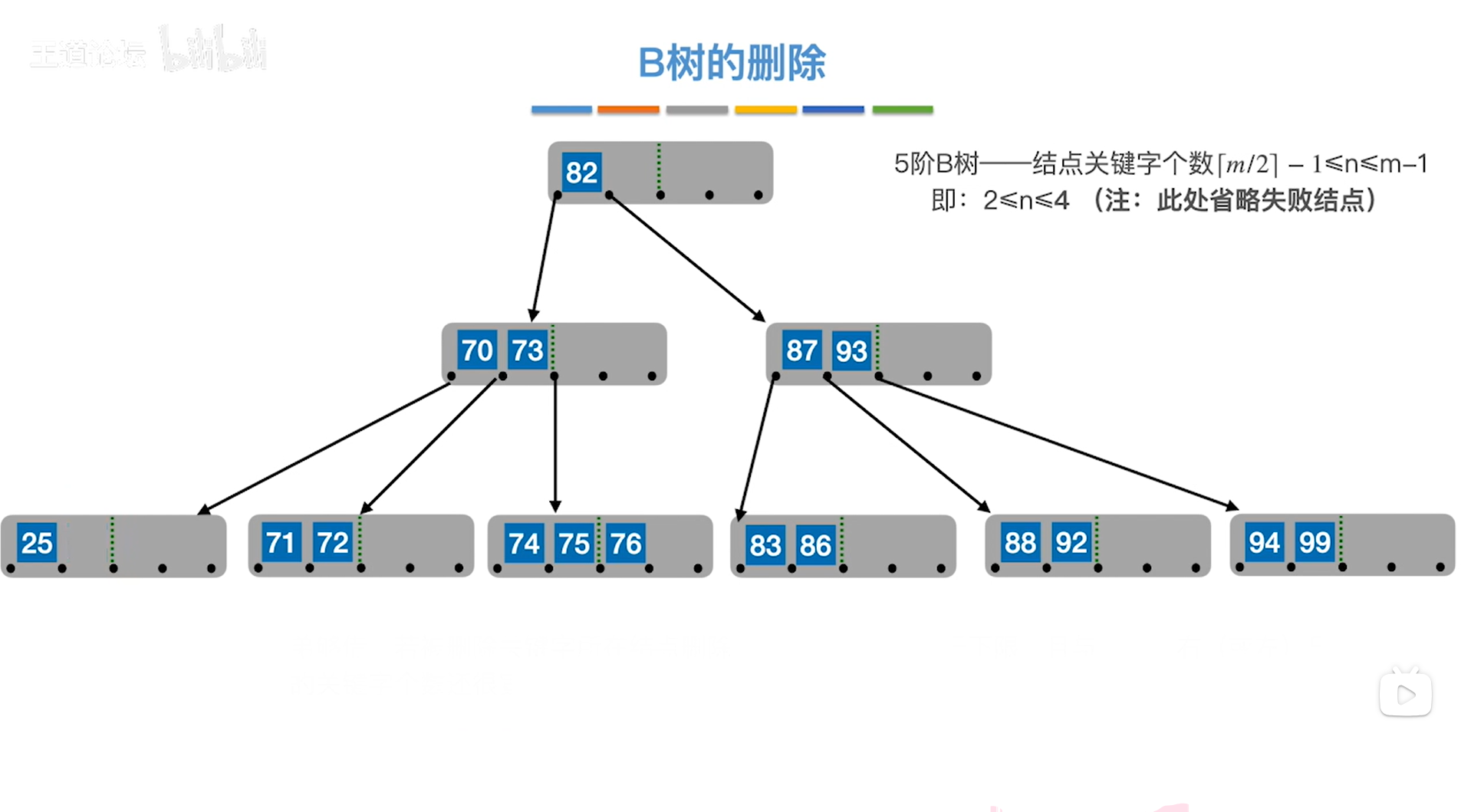
如上图,
删除49之后,49原来所在的结点中只有1个关键字25,低于1个结点中关键字个数的下限2,
那应该怎么解决呢?
注:结点中关键字是递增排序的
如果让只有1个关键字25的结点的右兄弟结点贡献一个关键字的话,该右兄弟结点中关键字的个数就会低于2,不符合5阶B树的特性,而且只有1个关键字25的结点没有左兄弟结点->情况二:"兄弟不够借",
因此可以把只有1个关键字25的结点和其右兄弟结点合并,
除了要合并只有1个关键字25的结点和其右兄弟结点外,还需要把这两个结点中间的关键字70给一起合并到结点中,
如下图:
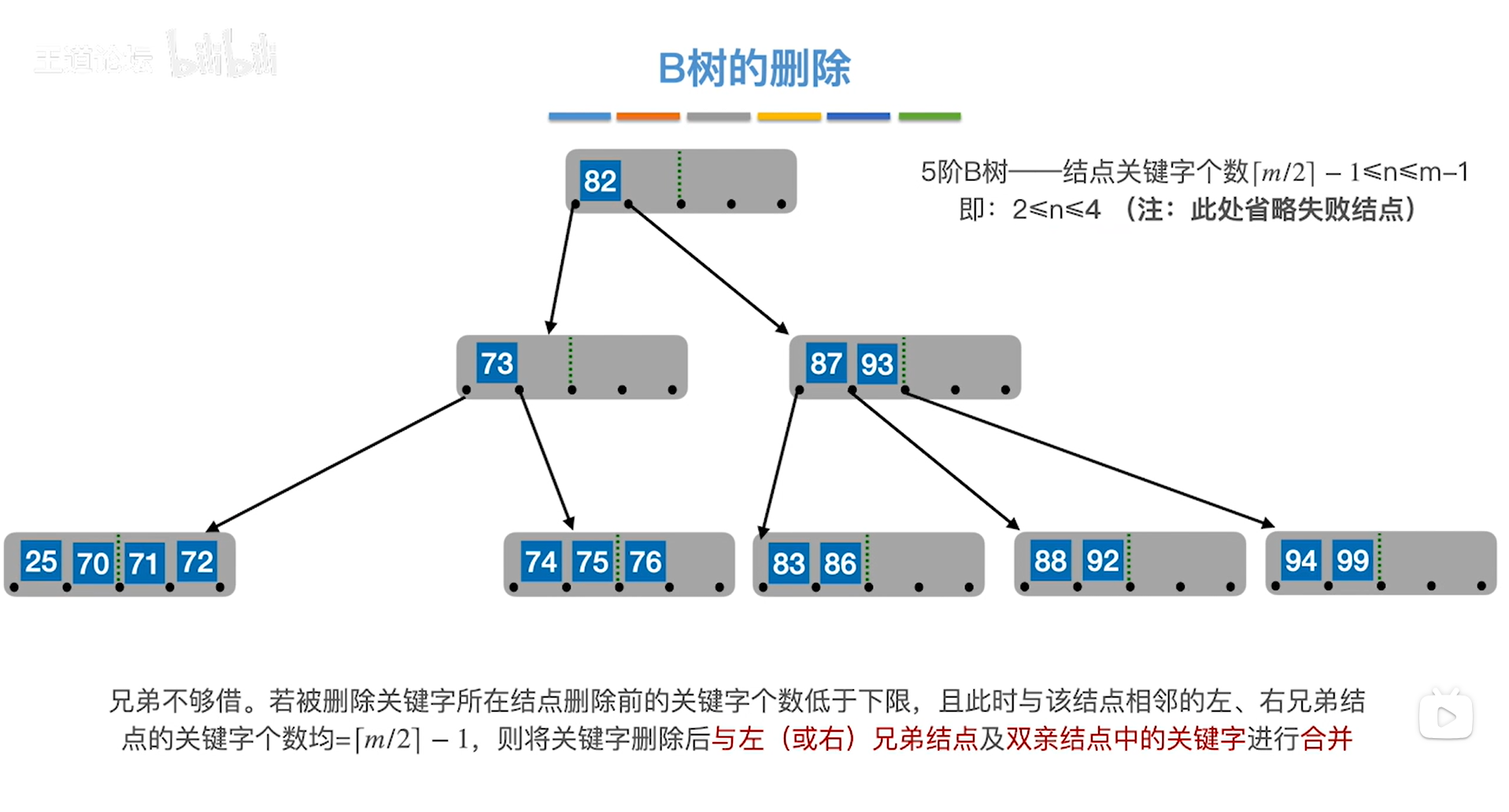
如上图,
由于刚才从包含关键字25的结点的父结点中借走了一个关键字70,此时只剩下关键字73,低于1个结点中关键字个数的下限2,也属于"兄弟不够借"的情况,
因此要把只包含关键字73的结点和其右兄弟结点(只包含关键字73的结点没有左兄弟结点)进行合并,
除了要合并只有1个关键字73的结点和其右兄弟结点外,还需要把这两个结点中间的关键字82给一起合并到结点中,
如下图:
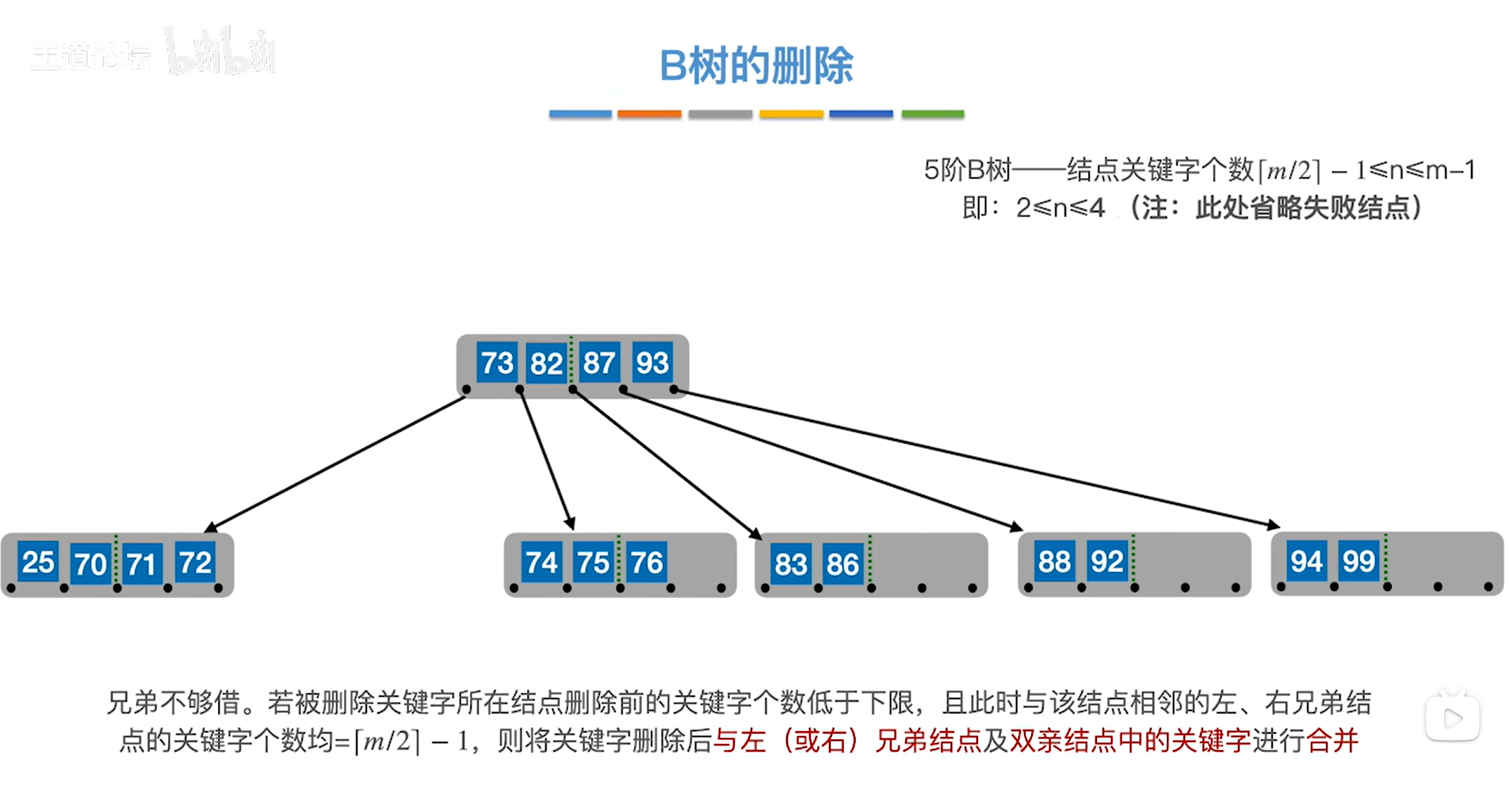
如上图,
此时符合5阶B树的特性。
2.总结:
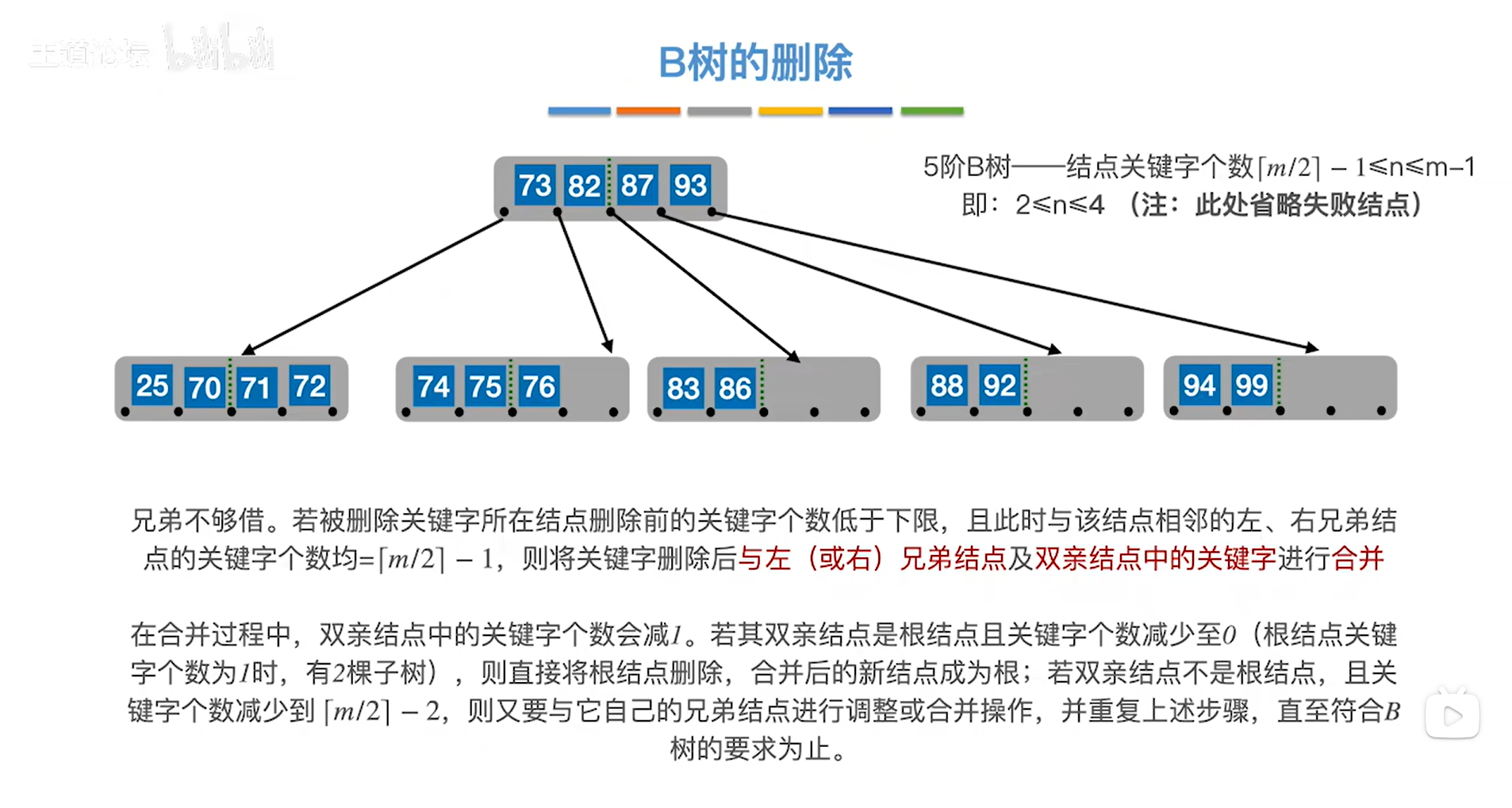
三.总结: