在对模型训练时,batch size盲目过大会导致GPU容量不够,因此通常会采用小批量训练。梯度积累技术的出现是为了让我们能够在逻辑上增大batch进行训练,嗯,逻辑上。
引用书中的原话就是:

书中首先引导我们思考一个问题,为什么神经网络在训练过程中会爆炸?就像之前跑项目的时候,常常会看到爆红,memory不够或受限,就其原因在于,主要的内存负担集中在向后传播这一过程,因为要计算梯度更新权重,就要存储向前传播时计算得到的激活值,当模型越大,激活值就越多,占用的空间越多。此时当batch也增大的时候,就会产生更多的激活值。
这样的恶性循环导致不得不减小batch,GA的存在能够帮助在内存限制下增加bacth大小。
Gradiants Accumulation
传统的mini-batch训练过程可以分为以下过程:
- 获取mini-batch
- 向前传播,存储激活值
- 向后传播:计算损失-->计算梯度-->更新权重
GA主要针对向后传播的最后一步做出改变,当前mini-batch的损失和梯度计算完成之后,并不更新权重,与随后几轮mini-batch计算得到的梯度累加后再进行计算。
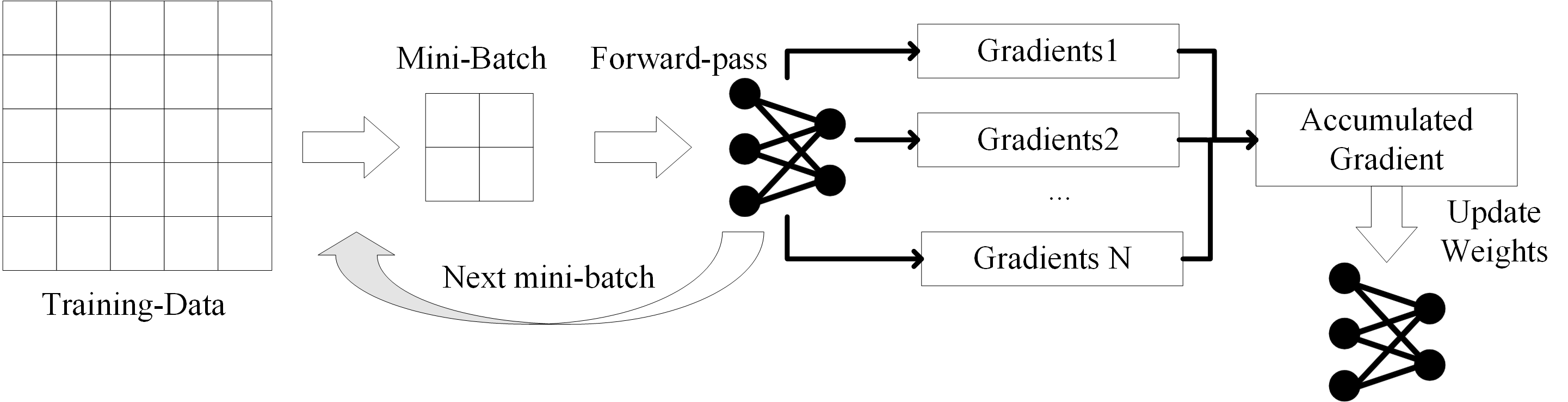
假设GPU最大的batch容量为16,但是我们想让batch达到64,该怎么做?
使用16的batch size,积累每一轮的gradients,每8个mini-batch更新一次权重,这样得到的batch值达到了16*8=128(官方给的栗子,可能是想凸显GA作用下batch会更灵活)
基于MINIST数据集的测试
官方给的笔记本基于MNIST数据集进行GA的测试。
受限导入必要的包
import sys
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import torch.nn.functional as F
import numpy as np
import pandas as pd
from time import time
from tqdm import tqdm
from torch.utils.data import DataLoader下载MNIST数据集的训练集和测试集
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))])
trainset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
trainloader = DataLoader(trainset, batch_size=32, shuffle=True)
testset = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform)
testloader = DataLoader(testset, batch_size=32, shuffle=False)定义一个简单的网络
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(28 * 28, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 128)
self.fc4 = nn.Linear(128, 10)
def forward(self, x):
x = x.view(x.size(0), -1)
x1 = torch.relu(self.fc1(x))
x2 = torch.relu(self.fc2(x1))
x3 = torch.relu(self.fc3(x2))
x4 = self.fc4(x3)
return x4定义评估函数
def evaluate(model):
model.eval()
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
inputs, labels = data
outputs = model(inputs) # use last element returned by forward function
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
return correct / total定义一个变量accumulation_steps = 4,即梯度累积步长为4
accumulation_steps = 4
net = Net()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)
for epoch in range(2):
net.train()
running_loss = 0.0
for idx, data in enumerate(trainloader):
inputs, labels = data
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
if ((idx + 1) % accumulation_steps == 0) or ((idx+1) == len(trainloader)):
optimizer.step()
optimizer.zero_grad()
running_loss += loss.item()
accuracy = evaluate(net)
print(f"Epoch {epoch + 1}, Loss: {round(running_loss / len(trainloader), 2)}, Accuracy: {accuracy * 100:.2f}%")再定义一个没有用到GA的训练循环做对比
net = Net()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)
for epoch in range(2):
net.train()
running_loss = 0.0
for idx, data in enumerate(trainloader):
optimizer.zero_grad()
inputs, labels = data
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
accuracy = evaluate(net)
print(f"Epoch {epoch + 1}, Loss: {round(running_loss / len(trainloader), 2)}, Accuracy: {accuracy * 100:.2f}%")如果成功运行了上面代码的话,我们会发现对运行时间上可能并没有什么作用,甚至不如普通的训练过程。作者也指出,GA的目标是减少总体内存使用。