SEA-RAFT：更简单、更高效、更准确的RAFT架构

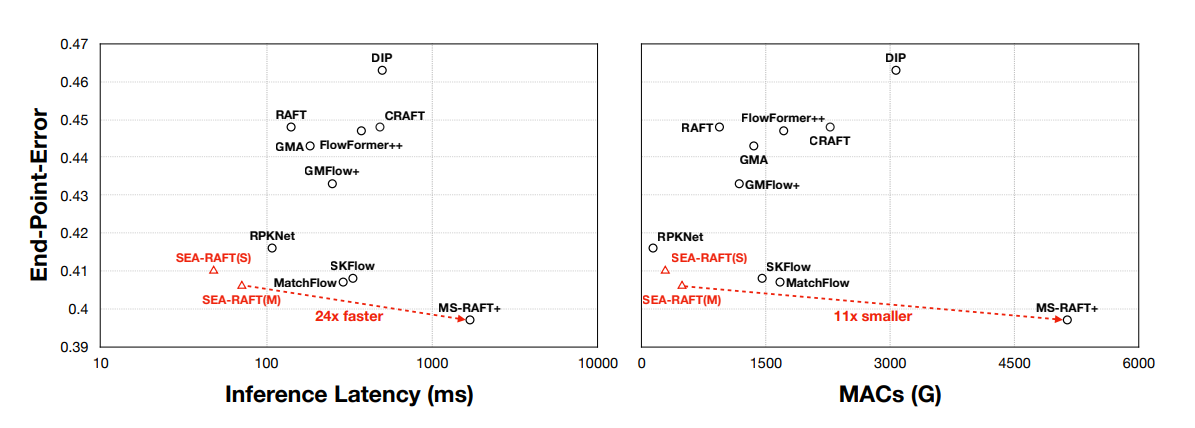
作者把SEA-RAFT的提升归功于以下三点：
New training loss: Mixture of Laplace（MoL）
SEA-RAFT没有使用绝对loss（比如L1，EPE等），而是预测MoL分布的参数，达到预测结果与GT flow之间的对数似然最大化。实验证明，MoL减少了对模糊情况的过拟合，提高了泛化能力。
Regress an initial flow Directly
通常，基于RAFT的方法会把光流初始化为0，然后通过多次迭代估计得到最终光流。SEA-RAFT选择直接使用context encoder预测初始光流，这种改动只增加了少量的计算开销，但是却极大地减少了迭代次数，推理效率提升明显（RAFT的迭代部分确实比较占资源）。
Rigid-motion pre-training
在TartanAir数据集上pre-train可以显著提升模型的泛化性，尽管TartanAir里的数据是由静态场景的相机运动产生的，光流多样性有限。

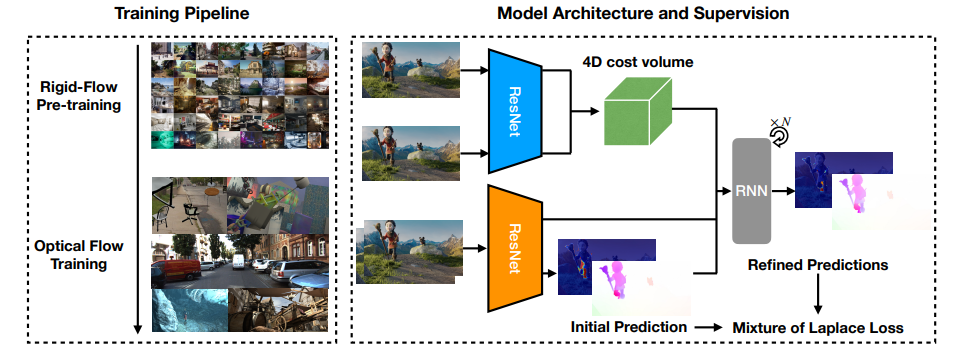
另外，作者额外提了一下：SEA-RAFT里提出的这些改动与RAFT-Style的方法是正交的关系，即改动可以比较容易地替换掉原先的模块。比如，模型结构（标准resnet替换feature encoder和context encoder，rnn替换gru等）

下面针对以上三点进行详细的描述：

iterative refinement

整体架构上延续了RAFT的做法，具体地，
给定两张连续的RGB图片$I_1$和$I_2$，$I_1$和$I_2$分别输入feature encoder，得到两张低分辨率的feature map：$F(I_1)$和$F(I_2)\in R^{h\times w\times D}$，然后$I_1$作为context encoder的输入，经过计算得到$C(I_1)\in R^{h\times w\times D}$。

根据向量内积计算相似性的原理，基于$F(I_1)$和$F(I_2)$创建了一个4D的相似性矩阵金字塔$[V_k]$。具体计算逻辑如下：

1. Reshape

$$F(I_1)\in R^{h\times w\times D}⟶F(I_1)\in R^{(h\times w)\times D}$$
$$F(I_2)\in R^{h\times w\times D}⟶F(I_2)\in R^{(h\times w)\times D}$$

2. Matrix multi

$$V=F(I_1)\ast F(I_2{)}^T$$

3. 构建4D相似性矩阵金字塔
   $$V_k=AvgPool2D(V,2^k)$$

所以，4D相似性金字塔里每个矩阵的shape为：
$$V_k\in R^{h\times w\times (\frac{h}{2^k})\times (\frac{w}{2^k})}$$

代码示例:

    def corr(fmap1, fmap2, num_head):
        batch, dim, h1, w1 = fmap1.shape
        h2, w2 = fmap2.shape[2:]
        fmap1 = fmap1.view(batch, num_head, dim // num_head, h1*w1)
        fmap2 = fmap2.view(batch, num_head, dim // num_head, h2*w2) 
        corr = fmap1.transpose(2, 3) @ fmap2
        corr = corr.reshape(batch, num_head, h1, w1, h2, w2).permute(0, 2, 3, 1, 4, 5)
        return corr  / torch.sqrt(torch.tensor(dim).float())

前两个维度始终保持最高分辨率，只在后两个维度上进行下采样。下采样是为了增加感受野，希望模型能够关注快速运动的物体，同时还能减小计算量；而前两个维度保持高分辨率可以保留更多有用信息，有利于模型关注学习较小的运动物体。

在RAFT的架构里，h和w设置为原始输入分辨率的1/8，4D相似性金字塔的层数设置为4，SEA-RAFT保留了这种配置。

在RAFT的架构采取了迭代式逐渐优化要预测的flow vector。初始flow vector设置为全0，即没有运动。每一次迭代时，使用当前的flow vector和一个查找半径$r$在4D相似性金字塔上提取运动特征。运动特征随即会被送入一个运动编码器MotionEncoder进一步提取运动信息。

查找半径$r$其实是一个三维的offset map，作用在上一次迭代输出的flow vector上。
假设$r=2$，offset map如下：
$\left[\begin{array}{c}(-2,-2),(-2,-1),(-2,0),(-2,1),(-2,2)\\ (-1,-2),(-1,-1),(-1,0),(-1,1),(-1,2)\\ (0,-2),(0,-1),(0,0),(0,1),(0,2)\\ (1,-2),(1,-1),(1,0),(1,1),(1,2)\\ (2,-2),(2,-1),(2,0),(2,1),(2,2)\end{array}\right]$

flow vector会与offset map中的每个元素相加，得到$2r+1$个flow vector，使用这些flow vector在4D相似性金字塔上提取相应的相似性信息，然后送入运动编码器计算提取运动特征。
这一步骤公式简化为：
$M=MotionEncoder(LookUp(V_k,\mu ,r))$

然后M送入RNN模块中进行下一次的预测：
$\acute{h}=RNN(h,M,C(I_1))$
$\Delta \mu =FLowHead(\acute{h})$

Mixture-of-Laplace Loss

部分光流训练数据中存在歧义，比如遮挡等，使得估计的光流与GT偏差较大，导致计算的loss（End-Point-Error）很大，这会在一定程度上误导模型优化方向。

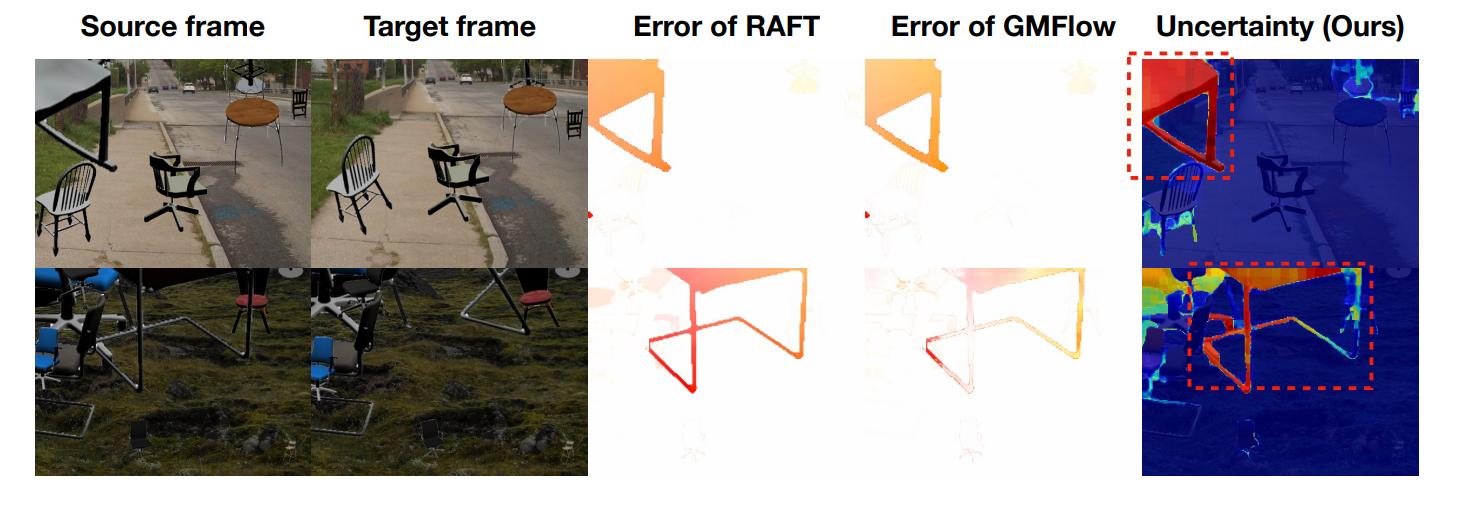
不再简单的计算End-Point-Error这种类L1的loss，而是计算模型预测光流的分布与实际光流分布的差异。
通常地，模型估计数据分布，一般选择常见的Gauss和Laplace分布，通过最大似然函数估计分布参数。

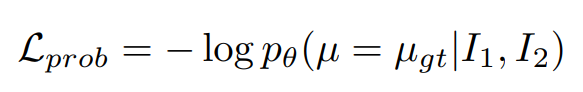
概率密度函数$p_{\theta }$由模型及其参数来表示。
SEA-RAFT选择使用Laplace分布作为模型要学习的分布函数$p_{\theta }$。所以loss可表示为：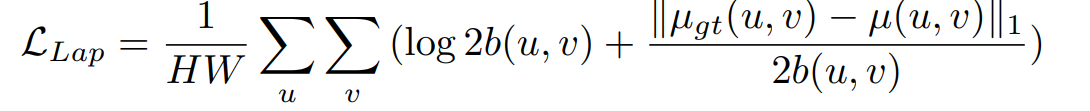
然而最大似然函数包含log项，loss中包含log项不利于训练收敛，所以模型直接预测log
设计了包含两项的loss：MoL

第一项：接近End-Point-Error这种类L1 loss，第二种则是Laplace分布
有一个参数α控制loss前后两项的权重，α由网络预测
Laplace分布的scale factor b也由网络预测，只不过是log b

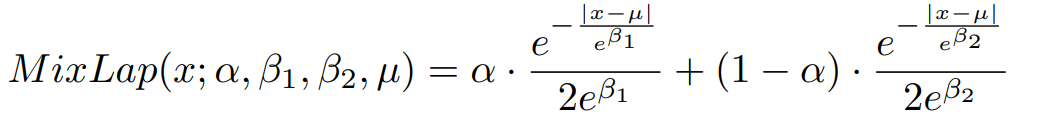
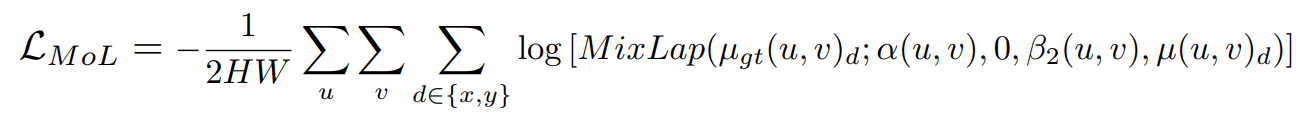
这样，既能在碰到正常样本时着重关注End-Point-Error，也能在歧义样本时关注不确定性的估计。

Direct Regression of Initial Flow

RAFT-style方法的iterative refinement通常会将初始光流初始化0，然而零初始化得到的光流与GT相差甚远，因此需要更多iteration去迭代优化。SEA-RAFT从Flow-Net的方法中借鉴了idea：给定前后两帧，直接利用context encoder估计一个初始光流。
这种方法显著提升了模型的收敛速度，在推理时可以降低iteration次数，从而降低计算量。

Large-Scale Rigid-Flow Pre-Training

先前大多数方法都是在一个小数据集上训练，数据样本少、场景多样性不够、不够真实。为了提升模型的泛化能力，SEA-RAFT在TartanAir数据集上进行了pre-train。TartanAir数据集提供了全景相机图像对的光流标签。TartanAir数据集里的这种运动形式可以看作是光流的一种特殊形式，静止场景，是改变了拍摄视角引起的运动。尽管缺乏运动的多样性，但是增加了运动的真实性和场景多样性，是模型具备了更好的泛化性。