单链表应用实践

发布于：2025-08-06 ⋅ 阅读:(20) ⋅ 点赞:(0)

目录

移除链表元素（力扣）

代码形成：

反转链表（力扣）

链表的中间结点（力扣）（快慢指针法）

思路：编辑

快慢指针实现代码

循环逻辑：

边界情况处理：

偶数长度的中间节点定义：

合并两个有序链表

代码实现：

申请空间，要释放

链表的回文结构

代码实现：

潜在改进点

思路：编辑

思路：编辑

移除链表元素（力扣）

https://leetcode.cn/problems/remove-linked-list-elements/description/

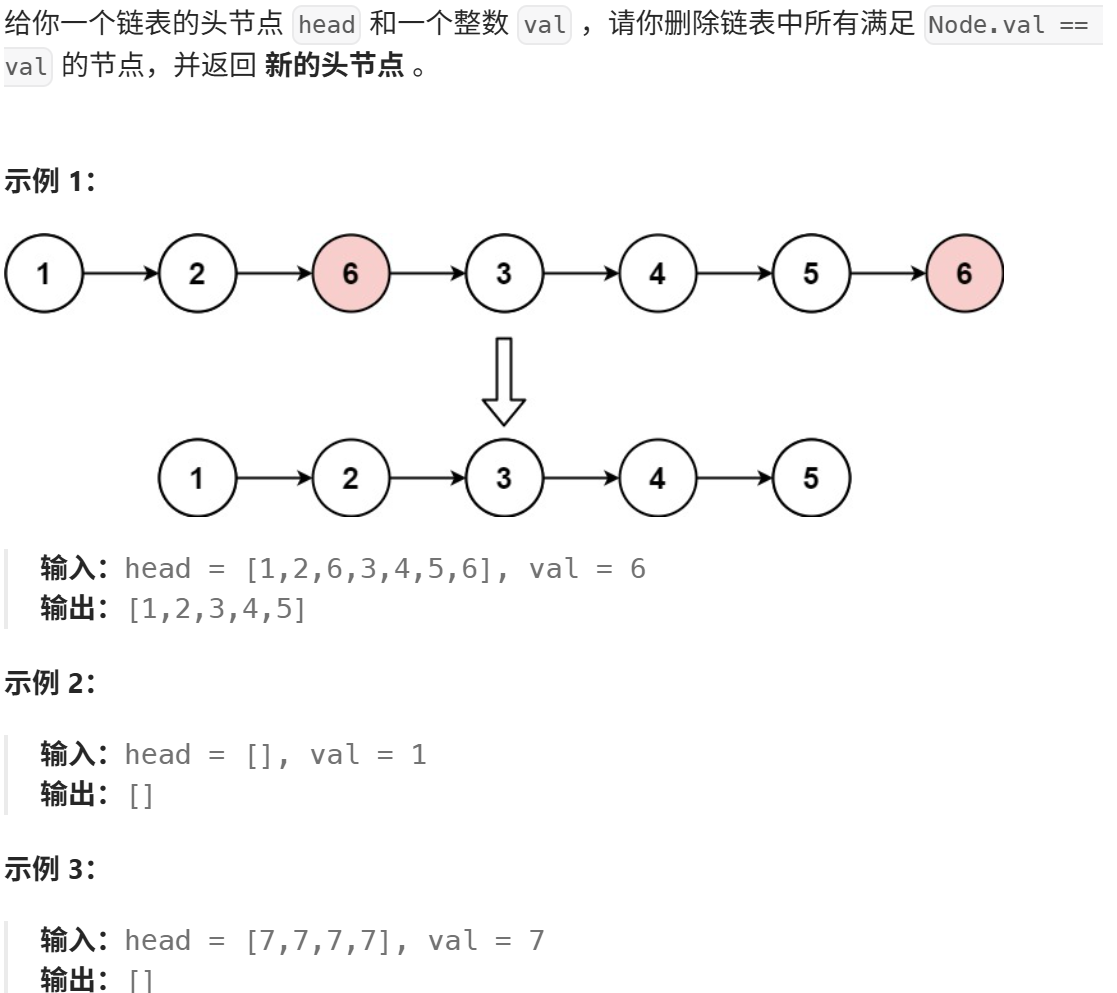
思路：

代码形成：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
 typedef struct ListNode ListNode;
struct ListNode* removeElements(struct ListNode* head, int val) {
    //创建空链表
    ListNode*newHead,*newtail;
    newHead=newtail=NULL;
    ListNode*pcur=head;
    while(pcur)
    {
        //把不为val的值插入新链表中
        if(pcur->val!=val)
        {
            //尾插
            //链表为空
            if(newHead==NULL)
            {
                newHead=newtail=pcur;
            }else
            {
                newtail->next=pcur;
                newtail=newtail->next;
            }
        }
        pcur=pcur->next;
    }
    if(newtail)
    newtail->next=NULL;
    return newHead;
}

注意：

newHead 和 newtail 用于维护新链表（存放所有不等于 val 的节点），初始为空。
pcur 用于遍历原链表，逐个检查节点的值
关键：原链表中被插入新链表的节点，其 next 指针可能指向原链表中的其他节点（甚至是需要删除的节点）。因此，新链表构建完成后，必须将尾节点的 next 置空，否则新链表可能包含不需要的节点或形成环。

反转链表（力扣）

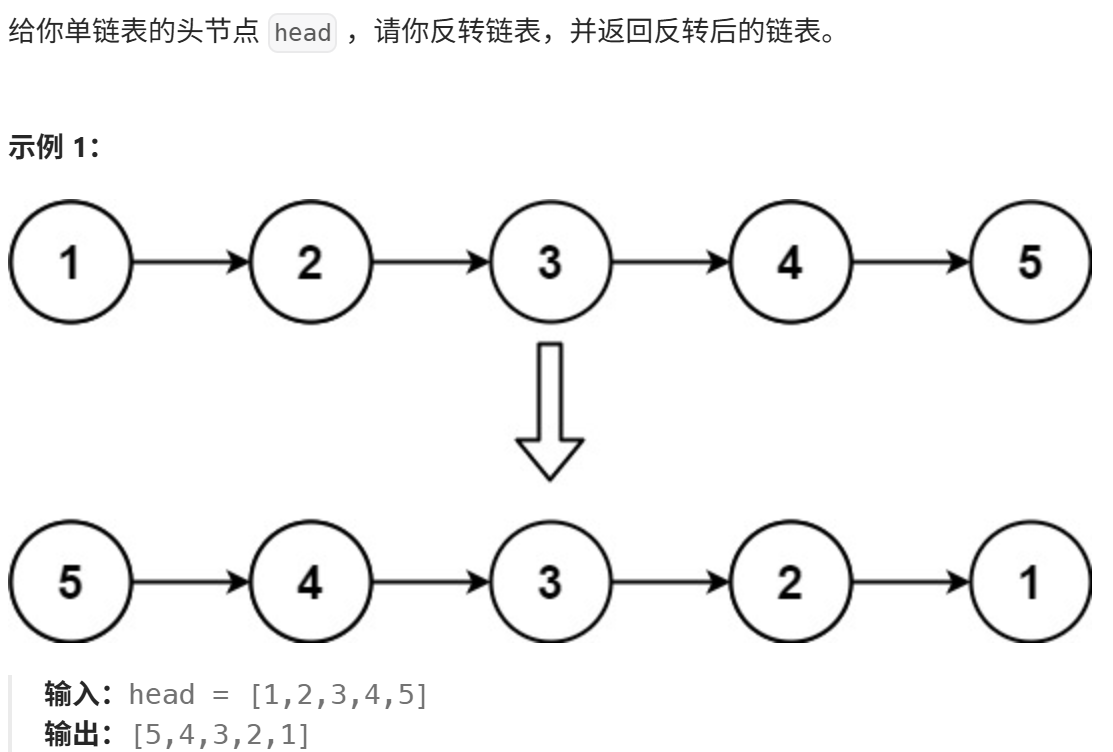
https://leetcode.cn/problems/reverse-linked-list/description/

思路：

通过三个指针（n1、n2、n3）逐步遍历链表，逐个反转节点的指向关系。具体来说：

n2 指向当前需要处理的节点

n1 指向 n2 的前一个节点（反转后 n2 要指向的节点）

n3 保存 n2 的下一个节点（防止反转后丢失后续节点）

通过循环让这三个指针依次后移，直到 n2 为空（遍历完所有节点），此时 n1 就是反转后链表的头节点。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */

struct ListNode* reverseList(struct ListNode* head) {
    //链表为空
     typedef struct ListNode ListNode;
    if(head==NULL)
    {
        return head;
    }//如果原链表为空（头节点为 NULL），直接返回 NULL，避免后续操作出错。
    //创建三个指针
    ListNode*n1,*n2,*n3;
    //初始化
    n1=NULL,n2=head,n3=n2->next;
    while(n2)
    {
        n2->next=n1;
        n1=n2;
        n2=n3;
        if(n3)
            n3=n3->next;
    }
    return n1;
}

注意：

代码正确处理了空链表的边界情况
当 n3 为 NULL 时（即 n2 是最后一个节点），不再执行 n3 = n3->next，避免空指针访问
整个过程只需要三个额外指针，空间效率高
反转后原链表的头节点会变成尾节点（next 为 NULL），符合链表规范

迭代法

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode ListNode;

struct ListNode* reverseList(struct ListNode* head) {
    // 终止条件：空链表或只有一个节点，直接返回
    if (head == NULL || head->next == NULL) {
        return head;
    }
    
    // 递归反转后续节点，得到反转后的头节点
    ListNode* newHead = reverseList(head->next);
    
    // 反转当前节点与下一个节点的指向
    head->next->next = head;  // 让下一个节点指向当前节点
    head->next = NULL;        // 当前节点成为尾节点，指向NULL
    
    return newHead;  // 始终返回反转后的头节点（原链表的最后一个节点）
}

适用于理解递归思想，但不适合长链表，可能会导致栈溢出

链表的中间结点（力扣）（快慢指针法）

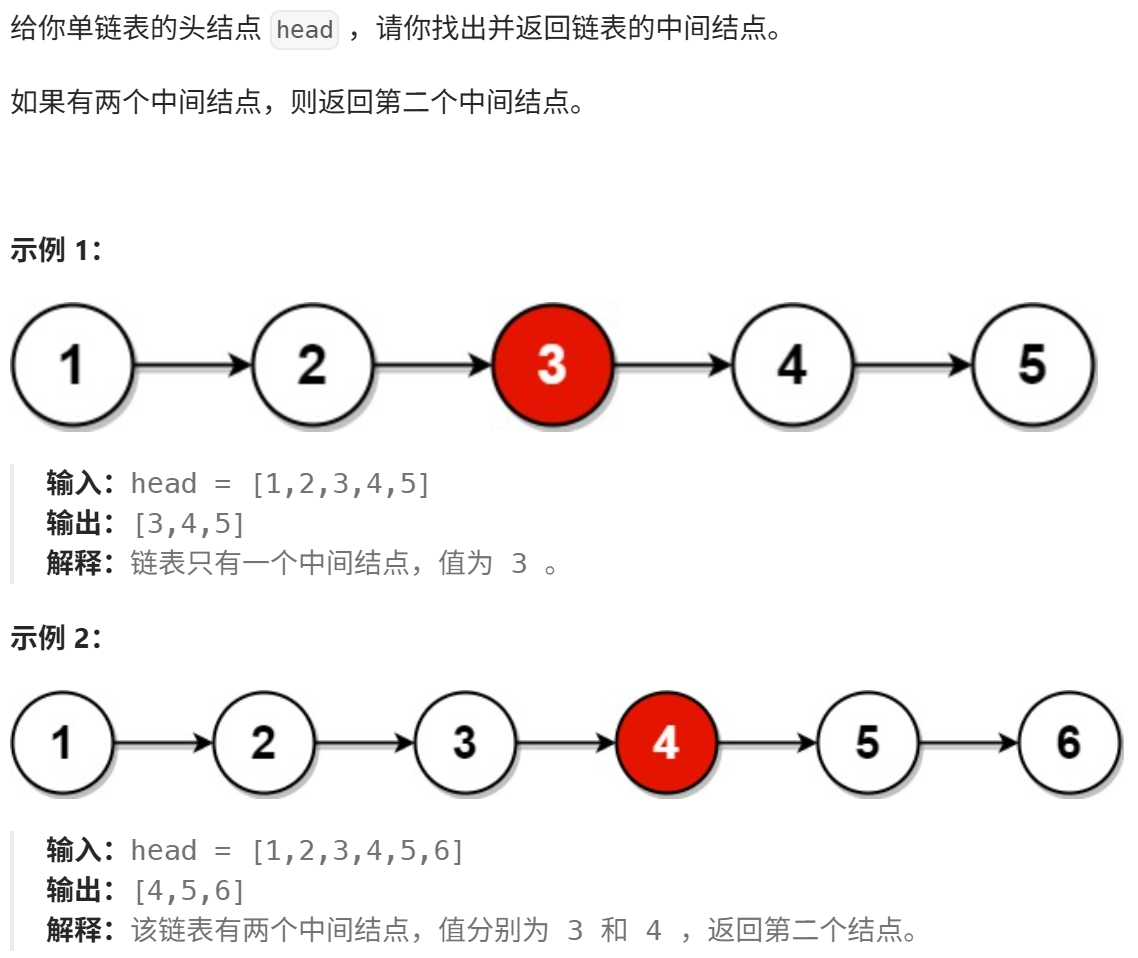
思路：

快慢指针实现代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {
    ListNode*l1,*l2;
    l1=l2=head;
    while(l1&&l1->next)
    {
        l1=l1->next->next;
        l2=l2->next;
    }
    return l2;
}

循环逻辑：

当 l1 能继续移动（即 l1 不为空且 l1->next 不为空）时，继续循环。
每次循环中，l1 前进 2 步，l2 前进 1 步，保持 l1 的速度是 l2 的 2 倍。
当循环结束时，l1 已到达或超过链表末尾，此时 l2 刚好在中间位置。

注意事项

边界情况处理：
- 若链表为空（head=NULL），快慢指针均为 NULL，直接返回 NULL，符合预期。
- 若链表只有一个节点，循环不执行，直接返回该节点，正确。
偶数长度的中间节点定义：
- 代码返回的是偶数长度链表的第二个中间节点（如 1->2->3->4 返回 3）。
- 若需要返回第一个中间节点（如 1->2->3->4 返回 2），只需调整循环条件为 while(l1->next && l1->next->next) 即可。

合并两个有序链表

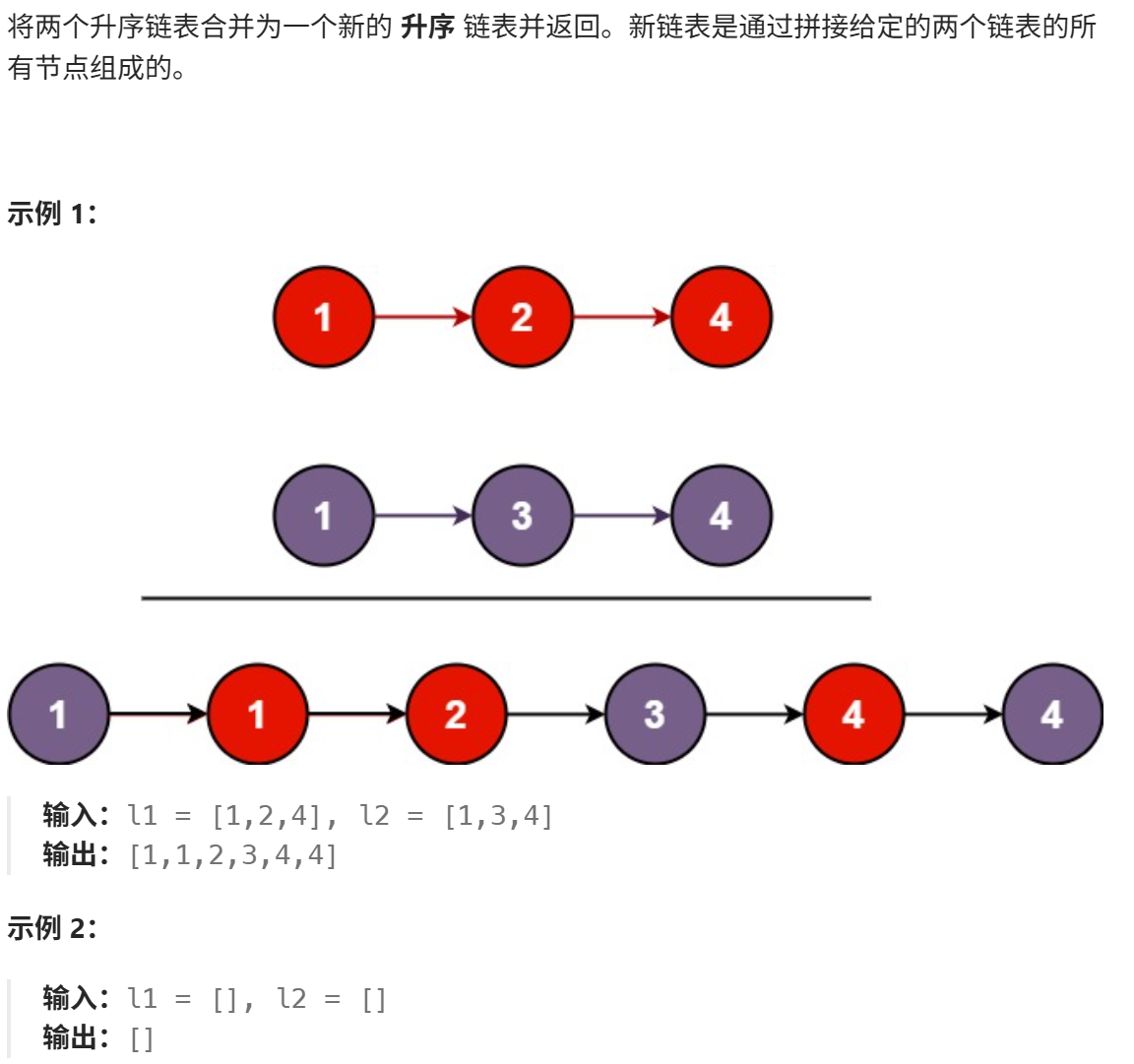
https://leetcode.cn/problems/merge-two-sorted-lists/description/

思路：

代码实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
    if (list1 == NULL)
        return list2;
    if (list2 == NULL)
        return list1;
    ListNode *newhead, *newtail;
    newhead=newtail = (ListNode*)malloc(sizeof(ListNode));//申请一个节点空间，非空结点
    while (list1 && list2) {
        if (list1->val < list2->val) {
            // 将1插入newhead后面
            newtail->next = list1;
            newtail = newtail->next;
            list1 = list1->next;
        }
        else
        {
            newtail->next = list2;
            newtail = newtail->next;
            list2 = list2->next;
        }
    }
    //总有一个先结束
    if(list1)
    {
        newtail->next=list1;
    }
    if(list2)
    {
        newtail->next=list2;
    }
    ListNode*rethead=newhead->next;
    free(newhead);
    newhead=NULL;
    return rethead;

}

哨兵节点（也称哑节点）是一个临时创建的空节点，用于简化链表操作（避免处理头节点为空的特殊情况）。
newhead 指向哨兵节点，newtail 始终指向新链表的尾节点（初始时与 newhead 相同）。

核心循环

while (list1 && list2) {  // 当两个链表都不为空时
    if (list1->val < list2->val) {
        newtail->next = list1;  // 将list1的当前节点接入新链表
        newtail = newtail->next;  // 尾指针后移
        list1 = list1->next;  // list1指针后移
    } else {
        newtail->next = list2;  // 将list2的当前节点接入新链表
        newtail = newtail->next;
        list2 = list2->next;
    }
}

循环结束条件：其中一个链表的节点被全部接入（list1 或 list2 为空）。
循环结束后，剩余未接入的节点一定是有序的（原链表本身有序），直接将其整体接入新链表尾部即可。

申请空间，要释放

ListNode* rethead = newhead->next;  // 新链表的真实头节点是哨兵节点的下一个
free(newhead);  // 释放哨兵节点（避免内存泄漏）
newhead = NULL;
return rethead;

优势：

时间复杂度：O (n + m)，其中 n 和 m 分别是两个链表的长度（每个节点仅遍历一次）。
空间复杂度：O (1)，仅使用常数级额外空间（哨兵节点在最后释放，不算有效空间）。
稳定性：保持原链表中相同值节点的相对顺序（例如：若两节点值相等，优先接入 list2 的节点，符合代码逻辑）。

改进：

newtail->next = list1 ? list1 : list2;

有一组遍历完后，使用这组更简便

链表的回文结构

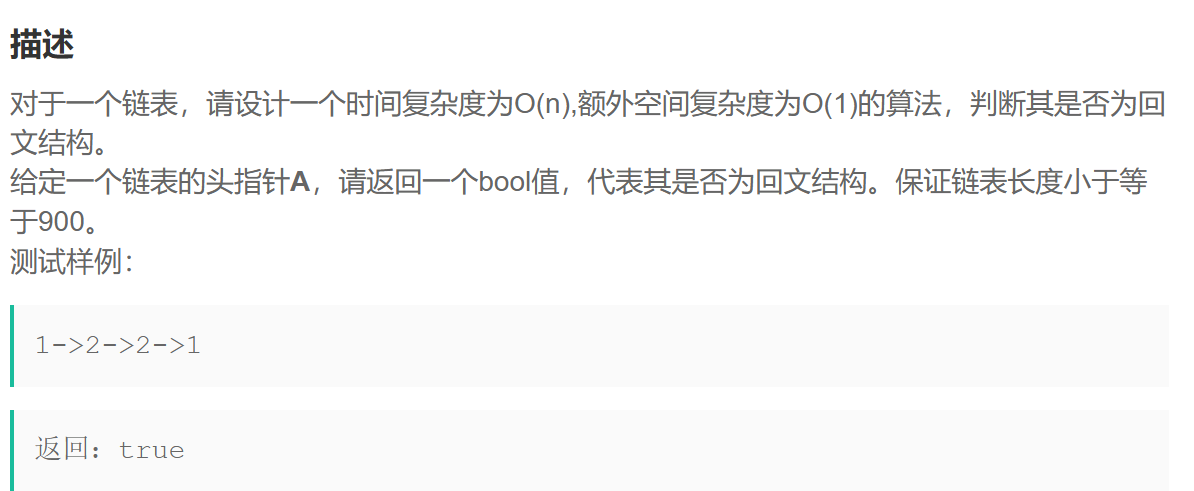
https://www.nowcoder.com/practice/d281619e4b3e4a60a2cc66ea32855bfa

思路1：

代码实现：

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};*/
class PalindromeList {
  public:
    bool chkPalindrome(ListNode* A) {
//创建数组-900
        int arr[900];
//遍历链表将值保存在数组中
        ListNode* pcur=A;
        int i = 0;
        while (pcur) {
            arr[i++] = pcur->val;
            pcur = pcur->next;
        }
//判断数组是否为回文结构
        int left = 0;
        int right = i - 1;
        while (left < right) {
            if (arr[left] != arr[right]) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
};

潜在改进点

数组大小固定的问题
- 目前数组大小固定为 900，如果链表长度超过 900，会导致数组越界
- 可以考虑使用动态分配内存（如new 操作符），根据实际链表长度创建数组
空间复杂度优化
- 目前空间复杂度为 O (n)，可以优化到 O (1)：
  - 找到链表中点
  - 反转后半部分链表
  - 比较前半部分和反转后的后半部分

思路2：

代码

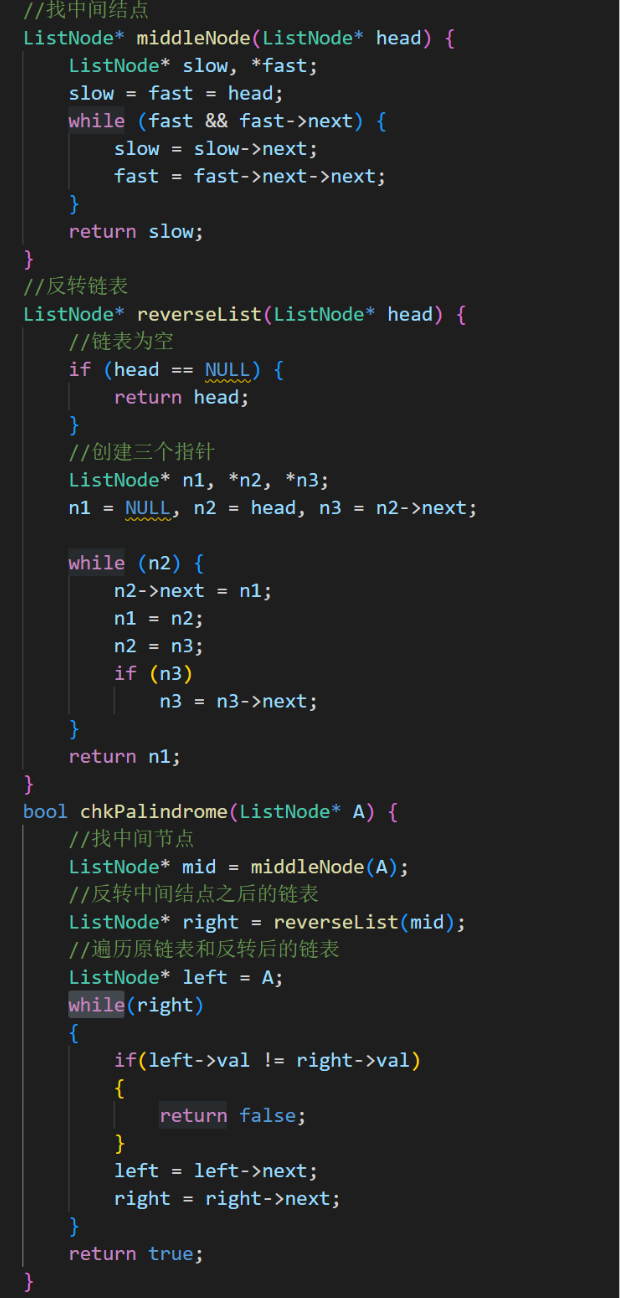
该方法相对复杂,但空间复杂度为o(1)

相交链表

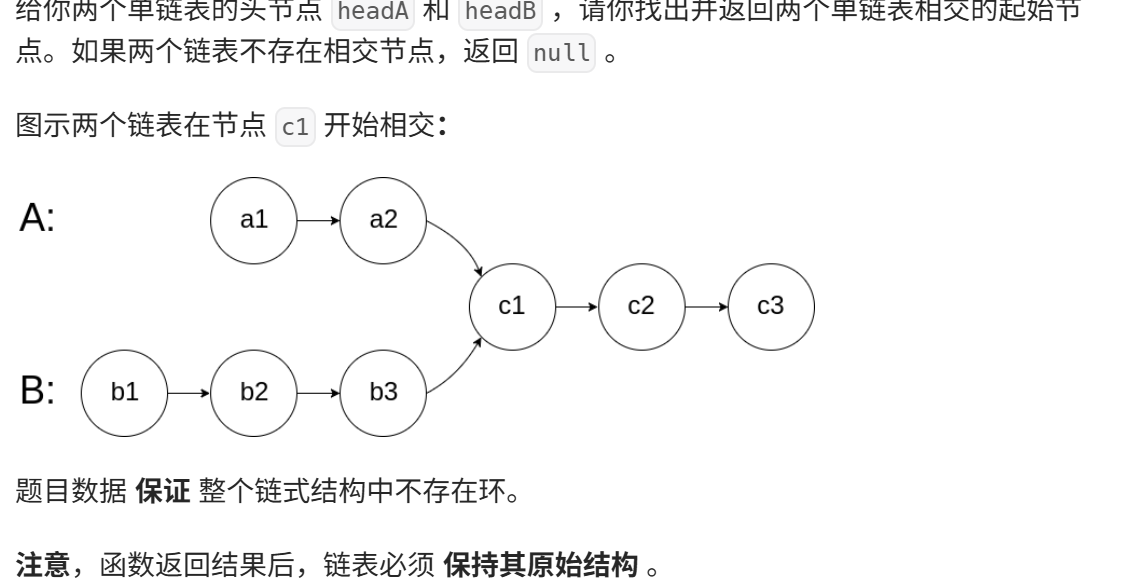
https://leetcode.cn/problems/intersection-of-two-linked-lists/description/

思路：

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
 typedef struct ListNode ListNode;

// 计算链表长度的函数
int getLength(ListNode* head) {
    int count = 0;
    ListNode* current = head;
    while (current) {
        count++;
        current = current->next;
    }
    return count;
}
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    // 计算两个链表的长度
    int lenA = getLength(headA);
    int lenB = getLength(headB);
    
    // 确定较长的链表和较短的链表
    ListNode* longList = lenA > lenB ? headA : headB;
    ListNode* shortList = lenA > lenB ? headB : headA;
    
    // 让较长的链表先走长度差的步数
    int diff = abs(lenA - lenB);
    for (int i = 0; i < diff; i++) {
        longList = longList->next;
    }
    
    // 同时移动两个链表的指针，寻找交点
    while (longList && shortList) {
        // 找到交点
        if (longList == shortList) {
            return longList;
        }
        longList = longList->next;
        shortList = shortList->next;
    }
    
    // 没有交点
    return NULL;
}

时间复杂度：O (n + m)，其中 n 和 m 分别是两个链表的长度
空间复杂度：O (1)，只使用了常数个额外空间

环形链表

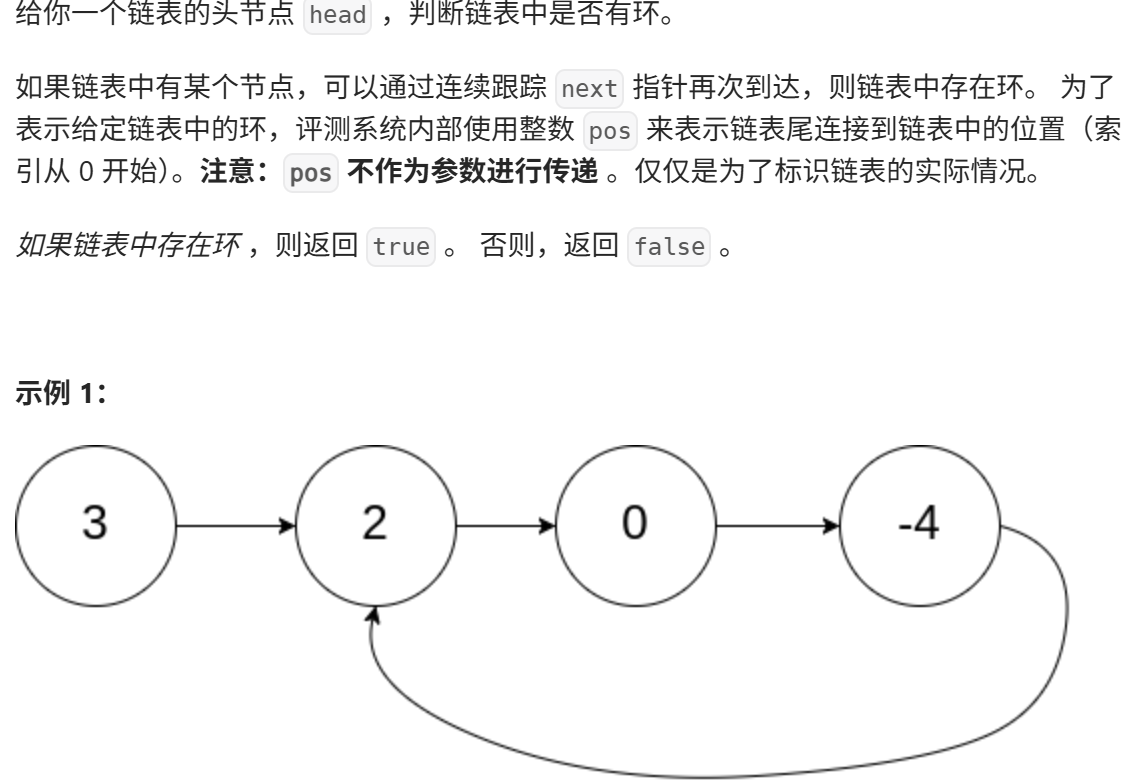
https://leetcode.cn/problems/linked-list-cycle/description/

思路：

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
 //快慢指针
 typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {
    ListNode*fast=head;
    ListNode*slow=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(slow==fast)
        {
            return true;
        }
    }
    return false;
}

时间复杂度：O (n)，其中 n 是链表的长度。在有环的情况下，快指针最多绕环一周就能追上慢指针
空间复杂度：O (1)，只使用了常数个额外空间，这是该算法相比哈希表方法的优势

环形链表2

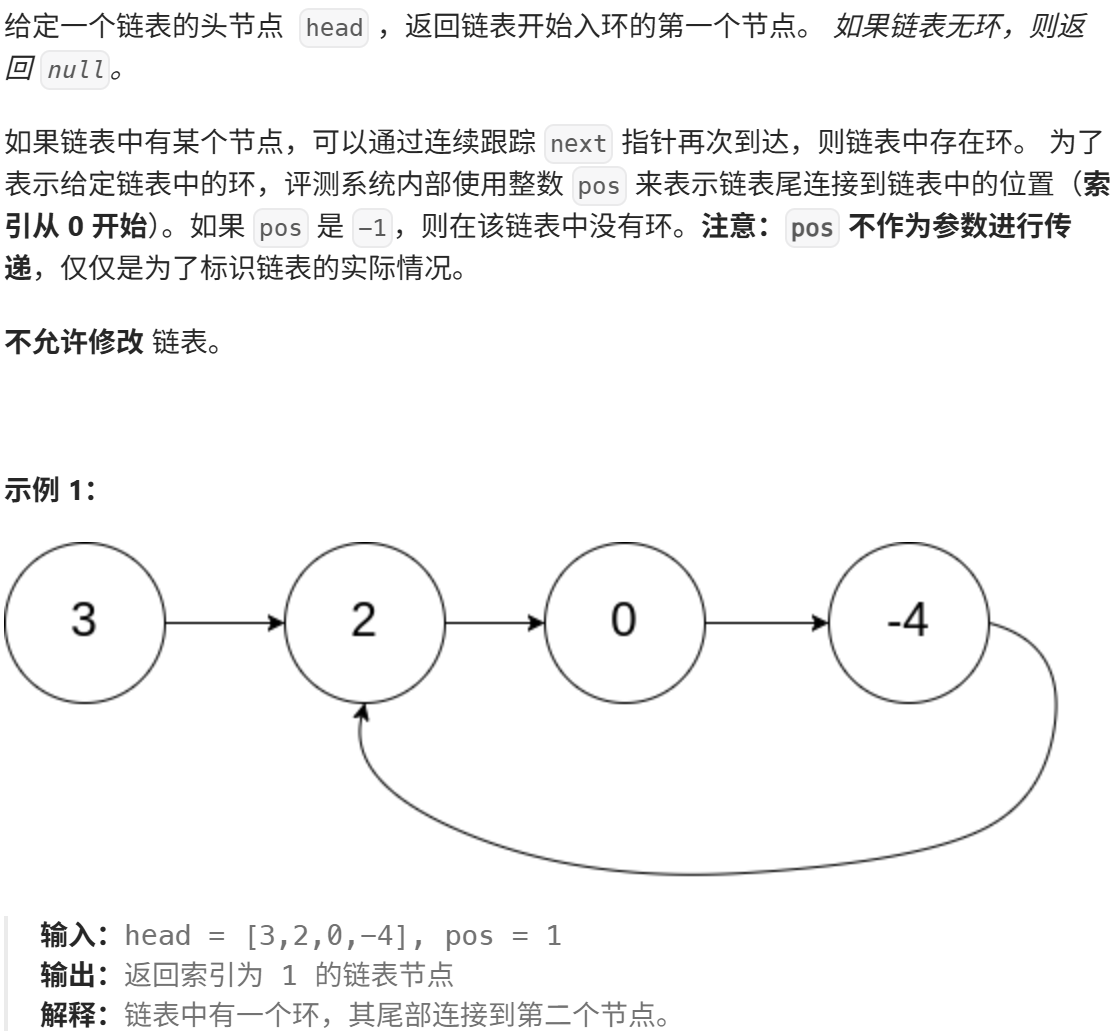
思路：

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
 typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {
    //快慢指针
    ListNode*slow=head;
    ListNode*fast=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)
        {
            ListNode*pcur=head;
            while(pcur!=slow)
            {
                //找进入环点
                pcur=pcur->next;
                slow=slow->next;
            } 
            return pcur;
        }
    }
    return NULL;
    
}

若链表存在环，快慢指针必定会在环内相遇（这是判断环存在的基础）
当快慢指针相遇后，将一个指针移到链表头部，两个指针以相同速度前进，它们再次相遇的位置就是环的入口节点

时间复杂度：O (n)，其中 n 是链表的长度
空间复杂度：O (1)，只使用了常数个额外空间