一.矩阵的定义
MATLAB 以矩阵作为数据操作的基本单位,这使得矩阵运算变得非常简捷、方便、高效。矩阵是由m*n个数q(i=1,2,…,m;j=1,2,…,n),排成的m行n列数表,记成

称为 mxn 矩阵,也可以记成aij或Am*n。其中,i表示行数,j表示列数。若 m=n,则该矩阵为n阶矩阵(n阶方阵)。
由有限个向量所组成的向量组可以构成矩阵,如果A=(aij)是mxn矩阵,那么A有m个n维行向量;有n个m维列向量。
矩阵的生成主要有直接输入法、M 文件生成法和文本文件生成法等。
二.MATLAB中矩阵的创建
1.按行直接输入
在键盘上直接按行方式输入矩阵是最方便、最常用的创建数值矩阵的方法,尤其适合较小的简单矩阵。在用此方法创建矩阵时,应当注意以下几点。
①输入矩阵时要以“[ ]”为其标识符号,矩阵的所有元素必须都在括号内。
②矩阵同行元素之间由空格(个数不限)或逗号分隔,行与行之间用分号或回车键分隔。
③矩阵大小不需要预先定义。
④矩阵元素可以是运算表达式。
⑤若“[ ]”中无元素,表示空矩阵。
⑥如果不想显示中间结果,可以用“ ;”结束。
>> a=[15 15 15;15 15 15;15 15 15]
a =
15 15 15
15 15 15
15 15 15
>> [[1 2 3];[2 4 6];[7 8 9]]
ans =
1 2 3
2 4 6
7 8 9
>> [[1,1+i,2];[2,3+2i,1]]
ans =
1.0000 + 0.0000i 1.0000 + 1.0000i 2.0000 + 0.0000i
2.0000 + 0.0000i 3.0000 + 2.0000i 1.0000 + 0.0000i2.M文件生成法
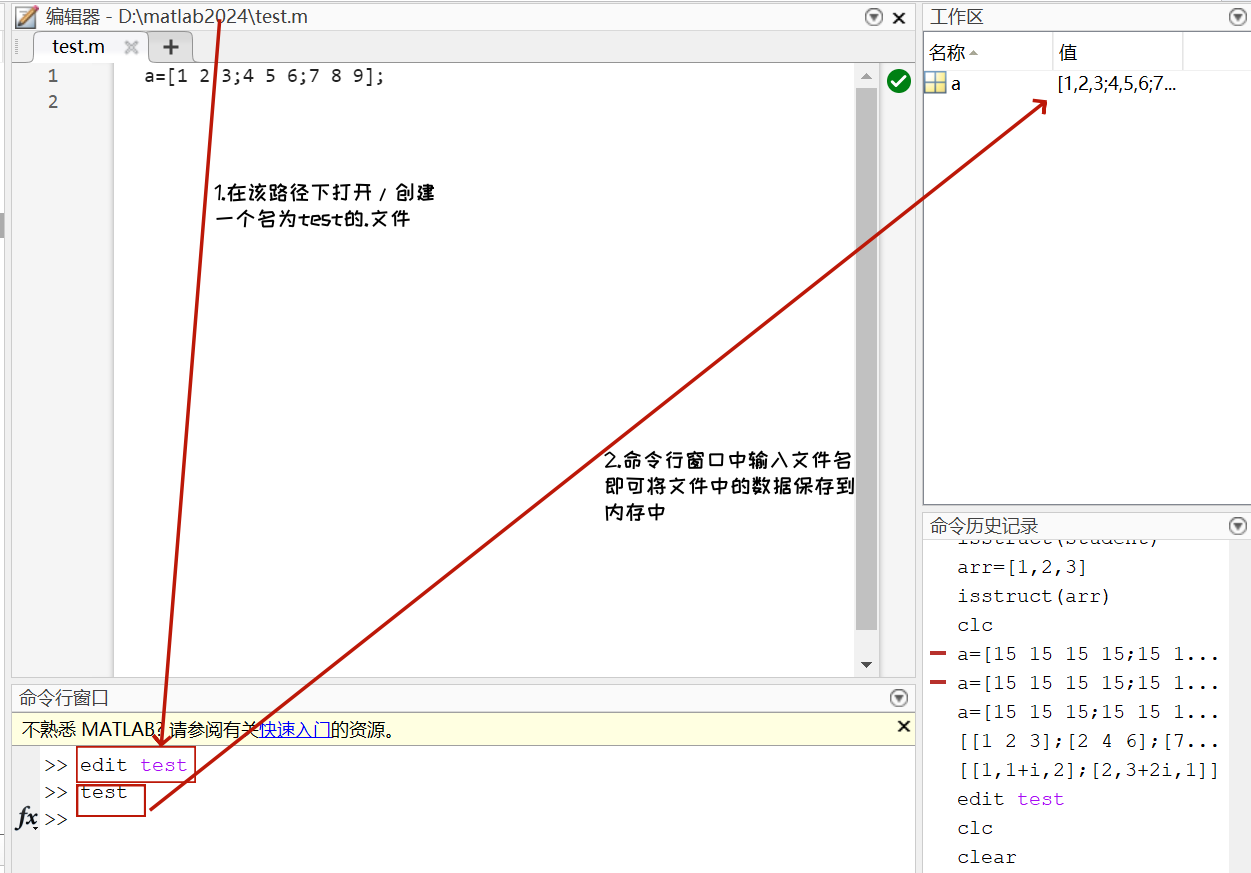
当矩阵的规模比较大时,直接输入法就显得笨拙,出差错也不易修改。为了解决这些问题,可以将所要输入的矩阵按格式先写入一文本文件中,并将此文件以m为其扩展名,即M 文件。
M 文件是一种可以在 MATLAB 环境下运行的文本文件,它可以分为命令式文件和函数式文件两种。在此处主要用到的是命令式M 文件,用它的简单形式来创建大型矩阵。在 MATLAB命令行窗口中输入 M 文件名,所要输入的大型矩阵即可被输入到内存中。
M 文件中的变量名与文件名不能相同,否则会造成变量名和函数名的混乱。运行 M文件时,需要先将 M文件sample.m 复制到当前目录文件夹下,否则运行时无法调用。
3.利用文本创建
MATLAB 中的矩阵还可以由文本文件创建,即在文件夹(通常为work文件夹)中建立txt 文件,在命令行窗口中直接调用此文件名即可。
(1)事先在记事本中建立文件。
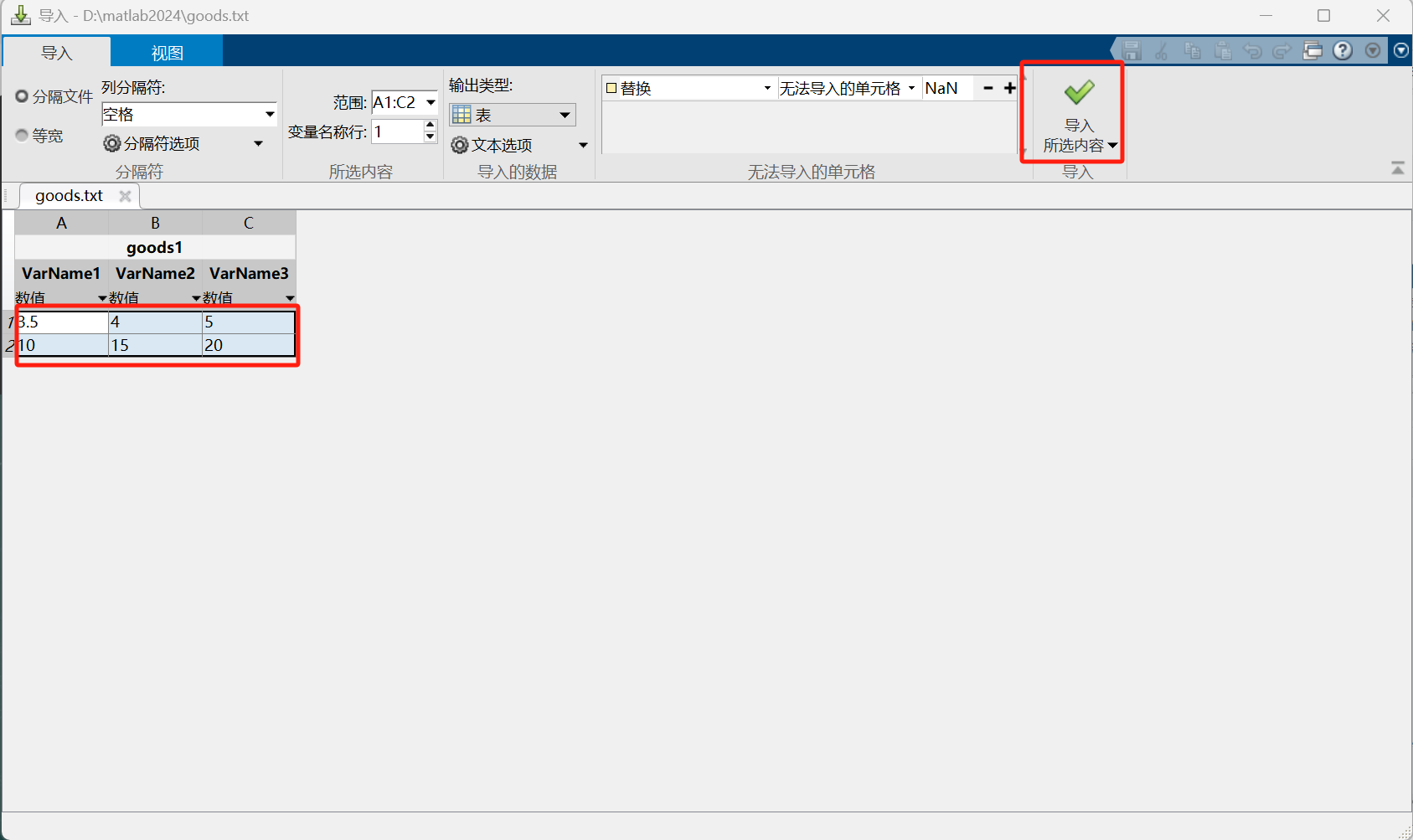
(2)以goods.txt保存,在MATLAB 命令行窗口中输入。
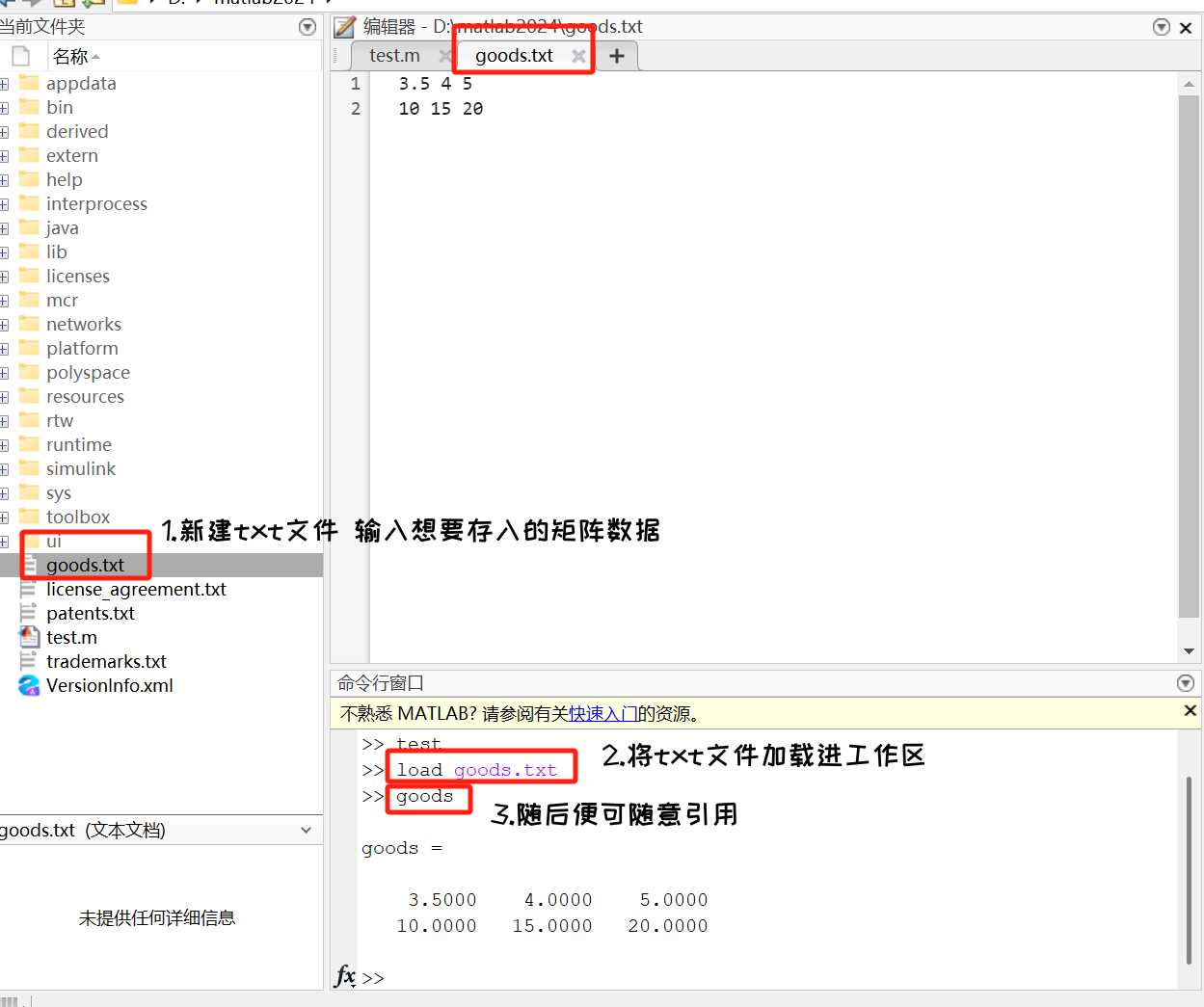
由此创建商品矩阵x。
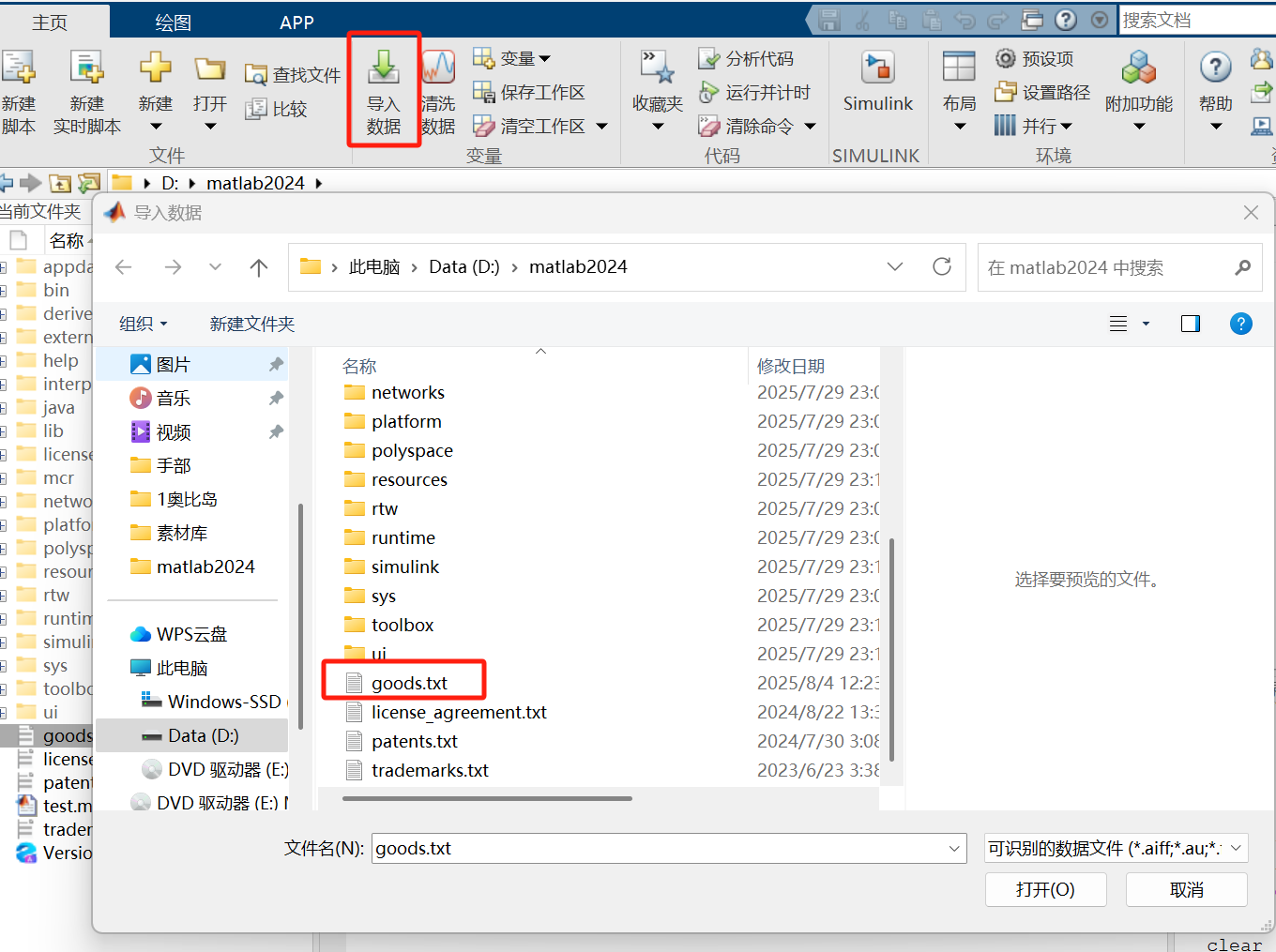
4.导入数据
三.MATLAB矩阵常用函数

(1)eye 函数:生成单位矩阵
>> E1=eye(3)
E1 =
1 0 0
0 1 0
0 0 1
>> E2=eye(2,4)
E2 =
1 0 0 0
0 1 0 0
>> E3=eye(size(E1))
E3 =
1 0 0
0 1 0
0 0 1
(2) ones 函数:生成全 1 矩阵
% 生成 3×3 全 1 矩阵
O1 = ones(3);
disp('ones(3) 生成的全 1 矩阵:');
disp(O1);
% 生成 2×4 全 1 矩阵
O2 = ones(2, 4);
disp('ones(2, 4) 生成的全 1 矩阵:');
disp(O2);
% 生成与矩阵 A 维数相同的全 1 矩阵
A = [1 2; 3 4; 5 6];
O3 = ones(size(A));
disp('ones(size(A)) 生成的全 1 矩阵(与 A 同维度):');
disp(O3);>> test
ones(3) 生成的全 1 矩阵:
1 1 1
1 1 1
1 1 1
ones(2, 4) 生成的全 1 矩阵:
1 1 1 1
1 1 1 1
ones(size(A)) 生成的全 1 矩阵(与 A 同维度):
1 1
1 1
1 1(3)eros 函数:生成全 0 矩阵
% 生成 3×2 全 0 矩阵
Z1 = zeros(3, 2);
disp('zeros(3, 2) 生成的全 0 矩阵:');
disp(Z1);
% 生成与矩阵 A 维数相同的全 0 矩阵
A = [1 2 3; 4 5 6];
Z2 = zeros(size(A));
disp('zeros(size(A)) 生成的全 0 矩阵(与 A 同维度):');
disp(Z2);>> test
zeros(3, 2) 生成的全 0 矩阵:
0 0
0 0
0 0
zeros(size(A)) 生成的全 0 矩阵(与 A 同维度):
0 0 0
0 0 0(4)rand 函数:生成均匀分布随机矩阵
每次运行结果不同,元素值在 0 到 1 之间随机 。
% 生成 3×3 在 [0,1] 区间均匀分布的随机矩阵
R1 = rand(3);
disp('rand(3) 生成的随机矩阵:');
disp(R1);
% 生成 2×4 在 [0,1] 区间均匀分布的随机矩阵
R2 = rand(2, 4);
disp('rand(2, 4) 生成的随机矩阵:');
disp(R2);
% 生成与矩阵 A 维数相同的随机矩阵
A = [1 2; 3 4];
R3 = rand(size(A));
disp('rand(size(A)) 生成的随机矩阵(与 A 同维度):');
disp(R3);>> test
rand(3) 生成的随机矩阵:
0.8147 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
rand(2, 4) 生成的随机矩阵:
0.9649 0.9706 0.4854 0.1419
0.1576 0.9572 0.8003 0.4218
rand(size(A)) 生成的随机矩阵(与 A 同维度):
0.9157 0.9595
0.7922 0.6557 (5)compan 函数:生成多项式伴随矩阵
% 多项式系数向量 P,对应多项式 x^3 + 2x^2 + 3x + 4 (注意系数按降幂排列,缺项补 0 )
P = [1 2 3 4];
C = compan(P);
disp('compan(P) 生成的伴随矩阵:');
disp(C);>> test
compan(P) 生成的伴随矩阵:
-2 -3 -4
1 0 0
0 1 0生成的伴随矩阵和多项式根等特性相关,可用于多项式分析 。
(6)diag 函数:生成对角矩阵
主对角线上是向量 v 的元素,其余为 0 。
% 以向量 v 的元素为对角线元素生成对角矩阵
v = [1 2 3];
D = diag(v);
disp('diag(v) 生成的对角矩阵:');
disp(D);>> test
diag(v) 生成的对角矩阵:
1 0 0
0 2 0
0 0 3
(7) hilb 函数:生成 Hilbert 矩阵
% 生成 3×3 Hilbert 矩阵
H = hilb(3);
disp('hilb(3) 生成的 Hilbert 矩阵:');
disp(H);>> test
hilb(3) 生成的 Hilbert 矩阵:
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000Hilbert 矩阵元素 H(i,j) = 1/(i + j - 1) ,是典型的病态矩阵,常用于测试算法稳定性 。
(8)magic 函数:生成魔方矩阵
% 生成 3 阶魔方矩阵(每行、每列、两条对角线元素和相等 )
M = magic(3);
disp('magic(3) 生成的魔方矩阵:');
disp(M);>> test
magic(3) 生成的魔方矩阵:
8 1 6
3 5 7
4 9 2magic(n) 函数生成的 n 阶魔方矩阵,是一个 n×n 的方阵,满足每行、每列以及两条主对角线上的元素之和都相等 ,这个相等的和值被称为幻和 。数学上,n 阶魔方矩阵幻和的计算公式是 S = n×(n² + 1)/2 。3 阶魔方矩阵经典结果是 [8 1 6; 3 5 7; 4 9 2] ,各行、列、对角线和为 15 。
(9)sparse 函数:生成稀疏矩阵
% 先创建一个普通矩阵 A
A = [0 0 1; 0 2 0; 3 0 0];
% 将 A 转化为稀疏矩阵形式
S = sparse(A);
disp('sparse(A) 生成的稀疏矩阵:');
disp(S);
% 查看稀疏矩阵存储方式(只存储非零元素的下标和值 )
disp('稀疏矩阵的存储内容:');
disp(full(S)); % full 函数可还原回普通矩阵查看 >> test
sparse(A) 生成的稀疏矩阵:
(3,1) 3
(2,2) 2
(1,3) 1
稀疏矩阵的存储内容:
0 0 1
0 2 0
3 0 0稀疏矩阵适合存储大部分元素为 0 的矩阵,节省内存,常用于大规模矩阵运算场景 。
四.MATLAB的矩阵运算
矩阵中的元素与向量中的元素一样,可以进行抽取引用、编辑修改等操作。
1.矩阵元素的修改
矩阵建立起来之后,还需要对其元素进行修改。表5-1列出了常用的矩阵元素修改命令。
(1)矩阵的扩充
>> A=eye(2)
A =
1 0
0 1
>> B=ones(2)
B =
1 1
1 1
>> C=[A B]
C =
1 0 1 1
0 1 1 1
>> D=[C;B A]
D =
1 0 1 1
0 1 1 1
1 1 1 0
1 1 0 1
>> 需要注意的是C的列数需要和B+A的一样
(2)矩阵中行的删除
>> C
C =
1 0 1 1
0 1 1 1
>> C(1,:)=[]
C =
0 1 1 1(3)矩阵中列的删除
>> C=[A B]
C =
1 0 1 1
0 1 1 1
>> C(:,2)=[]
C =
1 1 1
0 1 1(4)矩阵中元素的赋值
>> D=[A;B C]
D =
1 2 3
4 5 6
1 0 0
0 1 0
>> D(1,3)=5
D =
1 2 5
4 5 6
1 0 0
0 1 02.矩阵的变维
矩阵的变维可以用符号“ :”法和reshape 函数法。
①reshape 函数的调用
reshape(X,m,n),可将已知矩阵变维成m行n列的矩阵。
>> D(1,3)=5
D =
1 2 5
4 5 6
1 0 0
0 1 0
>> reshape(D,3,4)
ans =
1 0 0 6
4 2 1 0
1 5 5 0②“ :” 法
>> A=1:12
A =
列 1 至 11
1 2 3 4 5 6 7 8 9 10 11
列 12
12
>> C=zeros(3,4)
C =
0 0 0 0
0 0 0 0
0 0 0 0
>> C(:)=A(:)
C =
1 4 7 10
2 5 8 11
3 6 9 12变维是按列重新排的
3.矩阵的变向
C =
1 4 7 10
2 5 8 11
3 6 9 12
>> flipdim(C,1)
ans =
3 6 9 12
2 5 8 11
1 4 7 10
>> flipdim(C,2)
ans =
10 7 4 1
11 8 5 2
12 9 6 34.矩阵的抽取
对矩阵元素的抽取主要是指对角元素和上(下)三角阵的抽取。对角矩阵和三角矩阵的抽取命令见表 5-3。
(1)diag(X,k) 和 diag(X):抽取矩阵对角线元素
% 创建一个 4×4 矩阵
X = [1 2 3 4;
5 6 7 8;
9 10 11 12;
13 14 15 16];
% 抽取主对角线(k=0)元素,得到向量 [1,6,11,16]
d0 = diag(X);
disp('diag(X) 抽取主对角线结果:');
disp(d0);
% 抽取上方第 1 条对角线(k=1)元素,得到向量 [2,7,12]
d1 = diag(X,1);
disp('diag(X,1) 抽取上方第 1 条对角线结果:');
disp(d1);
% 抽取下方第 1 条对角线(k=-1)元素,得到向量 [5,10,15]
d_1 = diag(X,-1);
disp('diag(X,-1) 抽取下方第 1 条对角线结果:');
disp(d_1);>> test
diag(X) 抽取主对角线结果:
1
6
11
16
diag(X,1) 抽取上方第 1 条对角线结果:
2
7
12
diag(X,-1) 抽取下方第 1 条对角线结果:
5
10
15
k=0 对应主对角线,k>0 对应主对角线上方的对角线,k<0 对应主对角线下方的对角线,按此规则抽取对应位置元素组成向量 。
(2)diag(v,k) 和 diag(v):用向量构造对角矩阵
% 定义向量 v
v = [10,20,30];
% 构造主对角线为 v 的对角矩阵,得到 3×3 矩阵 diag(10,20,30)
M1 = diag(v);
disp('diag(v) 构造主对角线矩阵结果:');
disp(M1);
% 构造上方第 1 条对角线为 v 的矩阵,得到 5×5 矩阵(行数 = 向量长度 + |k| ,这里 k=1 ,所以 3 + 1 = 4 ?实际是 length(v)+abs(k) ,v 长度 3 ,k=1 ,得到 4×4 矩阵 )
M2 = diag(v,1);
disp('diag(v,1) 构造上方第 1 条对角线矩阵结果:');
disp(M2);>> test
diag(v) 构造主对角线矩阵结果:
10 0 0
0 20 0
0 0 30
diag(v,1) 构造上方第 1 条对角线矩阵结果:
0 10 0 0
0 0 20 0
0 0 0 30
0 0 0 0
diag(v) 会生成以 v 元素为主对角线的对角矩阵;diag(v,k) 则把 v 元素放到第 k 条对角线上,其余位置补 0 ,矩阵维度由向量长度和 k 共同决定 。
(3)tril 函数:提取下三角部分
% 还是用前面的 4×4 矩阵 X
X = [1 2 3 4;
5 6 7 8;
9 10 11 12;
13 14 15 16];
% 提取主下三角部分(主对角线及以下),得到下三角矩阵
T1 = tril(X);
disp('tril(X) 提取主下三角结果:');
disp(T1);
% 提取第 1 条对角线下面的部分(包括第 1 条对角线,k=1 ,即主对角线及下方 1 条对角线 )
T2 = tril(X,1);
disp('tril(X,1) 提取第 1 条对角线下面部分结果:');
disp(T2);
% 提取第 -1 条对角线下面的部分(k=-1 ,即主对角线下方第 1 条对角线及更下面 )
T3 = tril(X,-1);
disp('tril(X,-1) 提取第 -1 条对角线下面部分结果:');
disp(T3);>> test
tril(X) 提取主下三角结果:
1 0 0 0
5 6 0 0
9 10 11 0
13 14 15 16
tril(X,1) 提取第 1 条对角线下面部分结果:
1 2 0 0
5 6 7 0
9 10 11 12
13 14 15 16
tril(X,-1) 提取第 -1 条对角线下面部分结果:
0 0 0 0
5 0 0 0
9 10 0 0
13 14 15 0
tril(X) 直接提取主对角线及以下元素,形成下三角矩阵;tril(X,k) 依据 k 值确定提取范围,k 越大,包含的对角线越靠上,提取的下三角部分越 “大” 。
(4)triu 函数:提取上三角部分
% 基于矩阵 X 演示
X = [1 2 3 4;
5 6 7 8;
9 10 11 12;
13 14 15 16];
% 提取主上三角部分(主对角线及以上),得到上三角矩阵
U1 = triu(X);
disp('triu(X) 提取主上三角结果:');
disp(U1);
% 提取第 1 条对角线上面的部分(包括第 1 条对角线,k=1 ,即主对角线及上方 1 条对角线 )
U2 = triu(X,1);
disp('triu(X,1) 提取第 1 条对角线上面部分结果:');
disp(U2);
% 提取第 -1 条对角线上面的部分(k=-1 ,即主对角线上方第 1 条对角线及更上面 ,其实就是主对角线及以上 ,因为 k=-1 表示主对角线下方,取上面部分就是主对角线及以上 ,结果和 triu(X) 类似 )
U3 = triu(X,-1);
disp('triu(X,-1) 提取第 -1 条对角线上面部分结果:');
disp(U3);
>> test
triu(X) 提取主上三角结果:
1 2 3 4
0 6 7 8
0 0 11 12
0 0 0 16
triu(X,1) 提取第 1 条对角线上面部分结果:
0 2 3 4
0 0 7 8
0 0 0 12
0 0 0 0
triu(X,-1) 提取第 -1 条对角线上面部分结果:
1 2 3 4
5 6 7 8
0 10 11 12
0 0 15 16
triu(X) 提取主对角线及以上元素形成上三角矩阵;triu(X,k) 根据 k 确定提取范围,k 越小,包含的对角线越靠下,提取的上三角部分越 “大” ,和 tril 函数功能相反但逻辑类似 。
5.MATLAB矩阵基本运算
矩阵的基本运算包括加、减、乘、数乘、点乘、乘方、左除、右除、求逆等。其中加、减、乘与大家所学的线性代数中的定义是一样的,相应的运算符为+ - *
矩阵的除法运算是MATLAB所特有的,分为左除和右除,相应运算符为“\”和“/”。一般情况下,方程 A*X=B 的解是 X=A\B,而方程 X*A=B 的解是 X=B/A。
对于上述的四则运算,需要注意的是:矩阵的加、减、乘运算的维数要求与线性代数中的要求一致。
(1)矩阵的加减法
设A=(ai),B=(b)都是mxn矩阵,矩阵A与B的和记成A+B,规定为
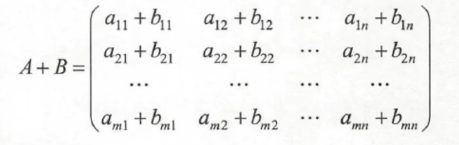
①交换律A+B=B+A
②结合律(A+B)+C=A+(B+C)
(2)矩阵的乘法运算
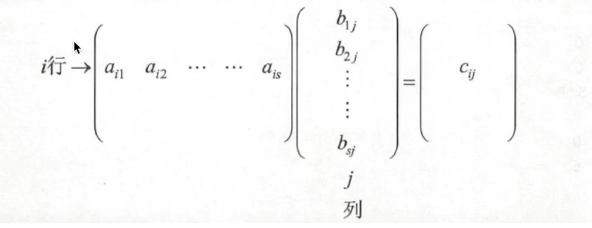
若3个矩阵有相乘关系,设A=(ai)是一个m*s矩阵,B=(b)是一个s*n矩阵,规定A与B的积为一个 m*n 矩阵 C=(cij)。
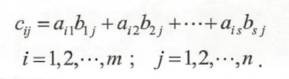
即 C=A*B,需要满足以下3种条件:
①矩阵4的列数与矩阵B的行数相同;
②矩阵C的行数等于矩阵A的行数,矩阵C的列数等于矩阵B的列数;
③矩阵C的第m行n列元素值等于矩阵A的m行元素与矩阵B的n列元素对应值积的和。
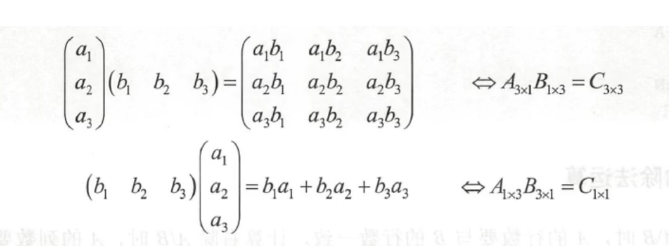
>> a=[1 2 3;4 5 6;7 8 9];
>> b=[4 5 6;7 8 9;10 11 12];
>> a*b
ans =
48 54 60
111 126 141
174 198 222注意:
①若矩阵A、B满足AB=0,未必有A=0或 B=0 的结论。
②AB≠BA,矩阵的乘法并不满足交换律。
(3)矩阵的点乘运算
点乘运算指将两矩阵中相同位置的元素进行相乘运算,将积保存在原位置组成新矩阵。
>> a=[1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> b=[4 5 6;7 8 9;10 11 12]
b =
4 5 6
7 8 9
10 11 12
>> a.*b
ans =
4 10 18
28 40 54
70 88 108(4)矩阵的除法运算
计算左除A\B时,A的行数要与B的行数一致。计算右除A/B时,A的列数要与B的列数一致。
①.左除运算
由于矩阵的特殊性,A*B通常不等于 B*A,除法也一样。因此除法要区分左右。线性方程组 D*X=B,如果D非奇异,即它的逆矩阵 inv(D)存在,则其解用 MATLAB 表示为X=inv(D)*B=D\B。符号“\”称为左除,即分母放在左边。
左除的条件:B的行数等于D的阶数(D的行数和列数相同,简称阶数)。
②.右除运算
若方程组表示为 X*D1=B1,D1非奇异,即它的逆阵 inv(D1)存在,则其解为X=B1*inv(D1)=B1/D1
符号“/”称为右除。
右除的条件:B1的列数等于D1的阶数(D1的行数和列数相同,简称阶数)。
5.MATLAB矩阵运算常用函数
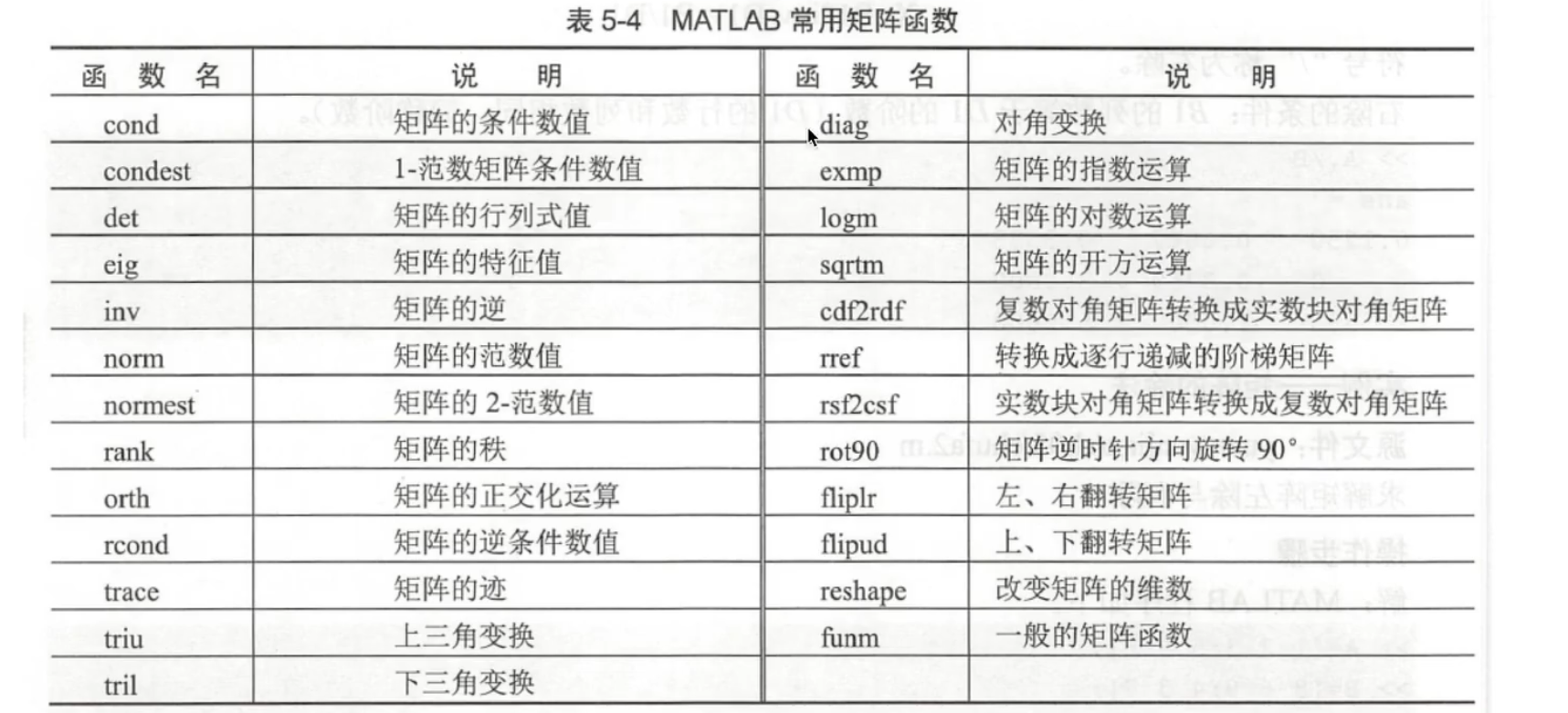
(1) 基础矩阵运算(行列式、逆、秩、迹)
% 定义一个测试矩阵
A = [1 2 3;
4 5 6;
7 8 9];
% 1. det:计算行列式
det_A = det(A);
disp('det(A) 行列式结果:');
disp(det_A); % 输出 0(因为矩阵行线性相关)
% 2. inv:计算矩阵的逆(注意:奇异矩阵无逆,这里换可逆矩阵演示)
B = [1 2; 3 4];
inv_B = inv(B);
disp('inv(B) 矩阵的逆:');
disp(inv_B); % 输出 [-2 1; 1.5 -0.5]
% 3. rank:计算矩阵的秩
rank_A = rank(A);
disp('rank(A) 矩阵的秩:');
disp(rank_A); % 输出 2(因为行线性相关)
% 4. trace:计算矩阵的迹(主对角线元素和)
trace_A = trace(A);
disp('trace(A) 矩阵的迹:');
disp(trace_A); % 输出 1+5+9=15>> test
det(A) 行列式结果:
6.6613e-16
inv(B) 矩阵的逆:
-2.0000 1.0000
1.5000 -0.5000
rank(A) 矩阵的秩:
2
trace(A) 矩阵的迹:
15
(2)特征值与范数
% 定义矩阵
C = [1 0; 0 2];
% 5. eig:计算特征值
eig_C = eig(C);
disp('eig(C) 特征值:');
disp(eig_C); % 输出 [1; 2](对角矩阵的特征值就是对角线元素)
% 6. norm:计算矩阵的范数(默认 2-范数)
norm_C = norm(C);
disp('norm(C) 矩阵范数(2-范数):');
disp(norm_C); % 输出 2(最大奇异值,对角矩阵的 2-范数是最大对角线元素)
% 7. normest:估算 2-范数(适合大矩阵快速计算)
normest_C = normest(C);
disp('normest(C) 估算 2-范数:');
disp(normest_C); % 输出 2(与 norm 结果一致)>> test
eig(C) 特征值:
1
2
norm(C) 矩阵范数(2-范数):
2
normest(C) 估算 2-范数:
2.0000
(3) 矩阵变换(三角矩阵、翻转、旋转)
% 定义矩阵
D = [1 2 3;
4 5 6;
7 8 9];
% 8. triu:提取上三角矩阵
triu_D = triu(D);
disp('triu(D) 上三角矩阵:');
disp(triu_D);
% 输出:
% 1 2 3
% 0 5 6
% 0 0 9
% 9. tril:提取下三角矩阵
tril_D = tril(D);
disp('tril(D) 下三角矩阵:');
disp(tril_D);
% 输出:
% 1 0 0
% 4 5 0
% 7 8 9
% 10. rot90:逆时针旋转 90°
rot90_D = rot90(D);
disp('rot90(D) 逆时针旋转 90°:');
disp(rot90_D);
% 输出:
% 3 6 9
% 2 5 8
% 1 4 7
% 11. fliplr:左右翻转
fliplr_D = fliplr(D);
disp('fliplr(D) 左右翻转:');
disp(fliplr_D);
% 输出:
% 3 2 1
% 6 5 4
% 9 8 7
% 12. flipud:上下翻转
flipud_D = flipud(D);
disp('flipud(D) 上下翻转:');
disp(flipud_D);
% 输出:
% 7 8 9
% 4 5 6
% 1 2 3>> test
triu(D) 上三角矩阵:
1 2 3
0 5 6
0 0 9
tril(D) 下三角矩阵:
1 0 0
4 5 0
7 8 9
rot90(D) 逆时针旋转 90°:
3 6 9
2 5 8
1 4 7
fliplr(D) 左右翻转:
3 2 1
6 5 4
9 8 7
flipud(D) 上下翻转:
7 8 9
4 5 6
1 2 3
(4)高级运算(条件数、指数、对数)
% 定义一个可逆且特征值全为正的矩阵(避免logm警告)
E = [4 1; 1 3]; % 特征值为5和2(均为正数,确保logm返回实数)
% 13. cond:计算条件数(衡量矩阵病态程度,值越大越病态)
cond_E = cond(E);
disp('cond(E) 条件数:');
disp(cond_E); % 输出约2.618(值较小,矩阵性态良好)
% 14. expm:矩阵的指数运算(基于矩阵幂级数)
expm_E = expm(E);
disp('expm(E) 矩阵指数:');
disp(expm_E);
% 输出指数矩阵(实数结果)
% 原理:expm(E) = sum_{k=0}^∞ (E^k / k!)
% 15. logm:矩阵的对数运算(expm的逆运算)
logm_E = logm(E);
disp('logm(E) 矩阵对数:');
disp(logm_E);
% 输出对数矩阵(实数结果,无警告)
% 验证:expm(logm_E) 应近似等于原矩阵E
disp('验证 logm 与 expm 的互逆性:');
disp(expm(logm_E)); % 输出接近原矩阵E
>> test
cond(E) 条件数:
1.9387
expm(E) 矩阵指数:
76.2898 40.4588
40.4588 35.8311
logm(E) 矩阵对数:
1.3470 0.2961
0.2961 1.0509
验证 logm 与 expm 的互逆性:
4.0000 1.0000
1.0000 3.0000
(5) 矩阵重构与简化
% 定义矩阵
F = [1 2 3 4;
5 6 7 8];
% 16. reshape:改变矩阵维度(元素按列优先重构)
reshape_F = reshape(F, 4, 2);
disp('reshape(F,4,2) 改变维度:');
disp(reshape_F);
% 输出:
% 1 5
% 2 6
% 3 7
% 4 8
% 17. rref:转换成行最简阶梯形
G = [1 2 3;
4 5 6;
7 8 9];
rref_G = rref(G);
disp('rref(G) 行最简阶梯形:');
disp(rref_G);
% 输出:
% 1 0 -1
% 0 1 2
% 0 0 0>> test
reshape(F,4,2) 改变维度:
1 3
5 7
2 4
6 8
rref(G) 行最简阶梯形:
1 0 -1
0 1 2
0 0 0
(6) 特殊矩阵运算
% 1. 先创建一个有复数特征值的矩阵(例如旋转矩阵)
A = [0 -1; 1 0]; % 特征值为 i 和 -i(共轭复数)
% 2. 求复数特征值和特征向量
[Vc, Dc] = eig(A); % Vc 是复数特征向量,Dc 是复数对角矩阵(特征值)
% 3. 使用 cdf2rdf 转换为实数块对角形式
[V, D] = cdf2rdf(Vc, Dc);
% 显示结果
disp('复数特征向量矩阵 Vc:');
disp(Vc);
disp('复数对角矩阵 Dc(特征值):');
disp(Dc);
disp('转换后的实数特征向量矩阵 V:');
disp(V);
disp('转换后的实数块对角矩阵 D:');
disp(D);>> test
复数特征向量矩阵 Vc:
0.7071 + 0.0000i 0.7071 + 0.0000i
0.0000 - 0.7071i 0.0000 + 0.7071i
复数对角矩阵 Dc(特征值):
0.0000 + 1.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 - 1.0000i
转换后的实数特征向量矩阵 V:
1.0000 0
0 -1.0000
转换后的实数块对角矩阵 D:
0 1
-1 0
6.MATLAB矩阵的幂运算
A是一个n阶矩阵,k是一个正整数,规定A^k=A*A*A*......*A(k个A相乘),称为矩阵的幂。其中k,l为正整数。
矩阵的幂运算是将矩阵中每个元素进行乘方运算,即:

在MATLAB中,幂运算就是在乘方符号" .^ "后面输入幂的次数。对于单个n阶矩阵A,A^k*A^l=A^(k+l),(A^K)^l=A^(k*l)。
对于两个n阶矩阵A与B,(A*B)^k≠A^k*B^k
7.MATLAB逆矩阵
(1)逆矩阵的定义
对于n阶方阵 A,如果有n阶方阵B满足AB=BA=I,则称矩阵A为可逆的,称方阵B为A的逆矩阵,记为 A^(-1)。
(2)逆矩阵的性质:
①若 A可逆,则A^(-1)是唯一的。
②若A可逆,则A^(-1)也可逆,并且(A^(-1))^(-1)=A。
③若n阶方阵A与B都可逆,则AB也可逆,且(AB)-1=B-A-。
④若 A可逆,则|A^(-1)|=|A|^(-1)
(3)奇异矩阵和非奇异矩阵:
我们把满足|A|≠0 的方阵 A称为非奇异的,否则就称为奇异的
(4)求解矩阵的逆使用函数 inv
调用格式:Y=inv(x)
(5)求解矩阵的逆条件数值使用函数 rcond
另外,常用的运算还有指数函数、对数函数、平方根函数等。用户可查看相应的帮助获得使用方法和相关信息。
8.MATLAB中矩阵的条件数
(1)矩阵的条件数
在数值分析中是一个重要的概念,在工程计算中也是必不可少的,它用于刻画一个矩阵的“病态”程度。
(2)条件数的定义
对于非奇异矩阵 A,其条件数的定义为cond(A)v=||A^-1||v *||A||v,其中v=1,2,……,F
它是一个大于或等于1的实数,当A的条件数相对较大,即cond(A)>>1时,矩阵A是“病态”的,反之是“良态”的。
9.MATLAB中矩阵的范式
范数是数值分析中的一个概念,它是向量或矩阵大小的一种度量,在工程计算中有着重要的作用。对于向量x∈R^n,常用的向量范数有以下几种。
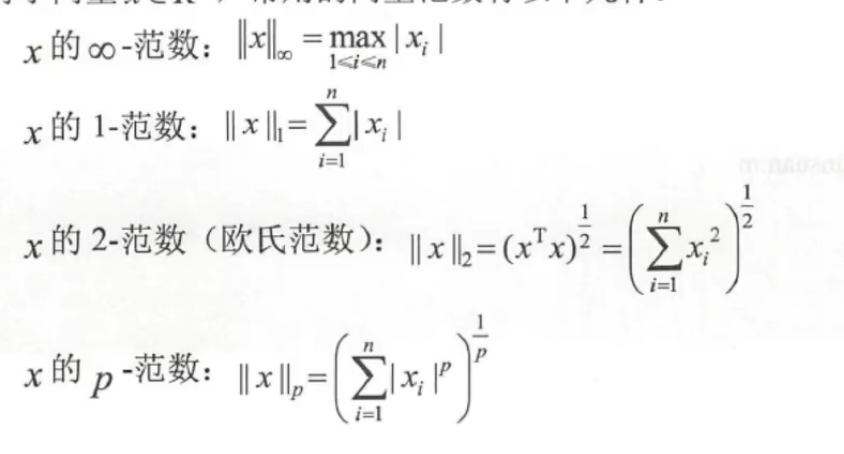

10.MATLAB中的奇异值分解

11.MATLAB中矩阵运算的方程求解
无论是在工程应用问题还是数学计算问题,方程都是问题转化的重要途径之一,通过将复杂的问题简单转化成矩阵的求解问题,最后在MATLAB 中进行函数计算。本节通过对一个方程组的应用来介绍如何介绍方程组的求解问题。

利用 MATLAB 中求解多元方程组的不同方法进行求解。
上面的方程符合Ax=b,首先需要确定方程组解的信息
系数矩阵 A 是由方程组中未知数 x1,x2,x3,x4 的系数按行排列构成的矩阵:
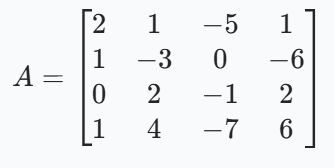
常数项向量 b 是方程组等号右边的常数按行排列构成的列向量:
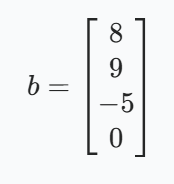
方法一:利用矩阵求逆(inv 函数 )
思路:如果矩阵 A 是可逆的(即行列式 det(A)≠0 ,满秩 ),那么方程组的解x=A^-1*b
% 定义系数矩阵 A
A = [2 1 -5 1; 1 -3 0 -6; 0 2 -1 2; 1 4 -7 6];
% 定义常数项向量 b
b = [8; 9; -5; 0];
% 计算矩阵 A 的逆矩阵
A_inv = inv(A);
% 求解方程组 Ax = b,得到解向量 x
x = A_inv * b;
% 显示解
disp('方程组的解为:');
disp(x);>> test
方程组的解为:
3.0000
-4.0000
-1.0000
1.0000首先通过 inv 函数求矩阵 A 的逆矩阵A_inv,然后将其与常数项向量 b 相乘,得到解向量 x 。
方法二:左除运算(\ 运算符 )
在 MATLAB 中,对于线性方程组 Ax = b ,更高效且数值稳定性更好的方法是使用左除运算符 \ ,代码如下:
% 定义系数矩阵 A
A = [2 1 -5 1; 1 -3 0 -6; 0 2 -1 2; 1 4 -7 6];
% 定义常数项向量 b
b = [8; 9; -5; 0];
% 直接使用左除运算求解
x = A \ b;
% 显示解
disp('方程组的解为:');
disp(x);>> test
方程组的解为:
3.0000
-4.0000
-1.0000
1.0000左除运算会根据矩阵 A 的特性(是否为方阵、是否满秩等 )自动选择合适的算法来求解方程组,一般优先推荐这种方法。
方法三:通过求秩和增广矩阵判断解的情况
在求解前,也可以先判断方程组解的情况,通过计算系数矩阵 A 的秩rank(A)和增广矩阵 [A|b]的秩rank([A b] 来确定:
% 定义系数矩阵 A
A = [2 1 -5 1; 1 -3 0 -6; 0 2 -1 2; 1 4 -7 6];
% 定义常数项向量 b
b = [8; 9; -5; 0];
% 构造增广矩阵
aug_matrix = [A b];
% 计算系数矩阵的秩和增广矩阵的秩
rank_A = rank(A);
rank_aug = rank(aug_matrix);
if rank_A == rank_aug && rank_A == size(A, 2)
disp('方程组有唯一解,求解结果如下:');
x = A \ b;
disp(x);
elseif rank_A == rank_aug && rank_A < size(A, 2)
disp('方程组有无穷多解');
else
disp('方程组无解');
end>> test
方程组有唯一解,求解结果如下:
3.0000
-4.0000
-1.0000
1.0000
这里 size(A, 2) 是获取矩阵 A 的列数(即未知数的个数 )。当系数矩阵的秩和增广矩阵的秩相等且等于未知数个数时,方程组有唯一解;当秩相等但小于未知数个数时,有无穷多解;当秩不相等时,方程组无解 。在你的这个例子中,一般是有唯一解的情况,然后再用左除等方法求解。
-----------------------------
编自2025/8/4和8/5。依旧无言