一、简介
贝叶斯分类是一类基于概率统计的分类算法的总称,这类算法均以18世纪英国数学家托马斯·贝叶斯提出的贝叶斯定理(Bayes' Theorem)为理论基础,故统称为贝叶斯分类。贝叶斯定理描述了在已知某些条件下,事件发生的概率如何随着新信息的获得而更新。
朴素贝叶斯分类(Naive Bayes Classifier)是贝叶斯分类中最简单且应用最广泛的一种分类方法。其"朴素"(Naive)一词源于该方法对特征条件做了一个很强的独立性假设:即假设所有特征之间都是相互独立的。尽管这个假设在实际中往往不成立,但朴素贝叶斯分类器在很多现实任务中仍然表现出色。
二、贝叶斯公式
要想运用朴素贝叶斯进行分类,我们必须深入理解贝叶斯公式及其工作原理。贝叶斯公式是概率论中的一个重要定理,描述了在已知某些条件下事件发生的概率。其数学表达式为:
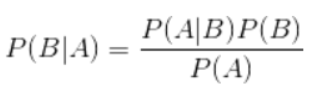
其中:
- P(A|B) 称为后验概率,表示在事件B发生的条件下事件A发生的概率
- P(B|A) 是似然概率,表示在事件A发生的条件下事件B发生的概率
- P(A) 是先验概率,表示事件A发生的初始概率
- P(B) 是边际概率,表示事件B发生的总概率
我们以在容器中的小球为例
容器A中有7个红球和3个白球,容器B中有1个红球和9个白球。我们需要计算在已知抽到红球的情况下,该红球来自容器A的概率。
根据贝叶斯定理,这个条件概率可以表示为:
P(A|红球) = [P(红球|A) × P(A)] / P(红球)
其中:
- P(红球|A) = 7/10(从容器A中抽到红球的概率)
- P(A) = 1/2(随机选择容器的先验概率,假设两个容器被选择的概率相等)
代入计算得: P(A|红球) = (7/10 × 1/2) ÷ (8/20) = 7/8 ≈ 87.5%
- P(红球) = (7+1)/(10+10) = 8/20(总体抽到红球的概率)
在贝叶斯定理的基础上结合全概公式,可以更全面地计算条件概率并处理复杂概率问题。以下是具体的扩展说明:
全概公式介绍:
- 公式:
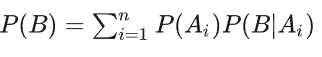
- 描述:将事件B的概率分解为多个互斥事件( Ai )下的条件概率之和。
- 公式:
结合两者我们就可以得到朴素贝叶斯的基本公式:
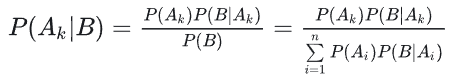
三、朴素贝叶斯分类器的基本表达方式
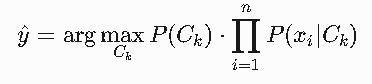
各组成部分详解
预测类别标签(y^)
- 表示算法输出的分类结果
- 例如:在垃圾邮件分类中,y^可能是"垃圾邮件"或"正常邮件"
- 在情感分析中,可能是"正面"、"中性"或"负面"
argmax_{C_k}运算
- 选择使后续表达式值最大的类别C_k
- 即对所有可能的类别计算后验概率,然后选择概率最大的那个类别
- 例如:假设有三个类别C1,C2,C3,分别计算P(C1|X),P(C2|X),P(C3|X),取最大值对应的类别
先验概率P(C_k)
- 表示类别C_k在训练数据中的比例
- 计算方式:P(C_k) = (训练集中类别C_k的样本数) / (总样本数)
- 例如:在1000封邮件中,有300封是垃圾邮件,则P(垃圾邮件)=0.3
条件概率连乘积∏_{i=1}^n P(x_i|C_k)
- 表示所有特征x_1到x_n在类别C_k下的条件概率的乘积
- 每个P(x_i|C_k)表示在类别C_k中,特征x_i出现的概率
- 例如:在垃圾邮件分类中,x_i可能是"免费"这个词,P(x_i|C_k)表示在垃圾邮件中"免费"出现的概率
特征独立性假设
- 这是"朴素"一词的来源,假设各特征之间相互独立
- 这使得计算大大简化,但现实中特征往往存在相关性
- 尽管如此,朴素贝叶斯在实际应用中仍表现良好
四、朴素贝叶分类函数
# sklearn.naive_bayes.MultinomialNB 参数详解
## alpha
**作用**:平滑参数(拉普拉斯/Lidstone平滑),默认值为1.0,用于防止零概率问题
**详细说明**:
- 当某个特征在训练集中未出现在某个类别时,会导致条件概率为0,通过平滑处理可以避免这种零概率问题
- 典型应用场景:文本分类中处理未出现的词汇
- 值越大,平滑效果越强(减少过拟合风险):
- 例如:alpha=1.0 比 alpha=0.5 平滑效果更强
- 特殊处理:
- 若设为0且 force_alpha=False,会自动调整为1e-10以避免数值错误
- 当force_alpha=True时,即使alpha接近0也会保持原值
## fit_prior
**作用**:是否从数据中学习类别先验概率,默认为 True
**行为细节**:
- True(默认):
- 根据训练数据计算各类别先验概率
- 计算公式:P(y=class_k) = (类k的样本数) / (总样本数)
- 示例:假设训练集有100个样本,其中A类60个,B类40个,则先验概率为[0.6, 0.4]
- False:
- 假设所有类别先验概率均等
- 计算公式:P(y=class_k) = 1 / (类别总数)
- 示例:对于3分类问题,每个类别的先验概率为1/3≈0.333
## class_prior
**作用**:手动指定类别先验概率,覆盖 fit_prior的设置
**使用规范**:
- 格式要求:
- 必须传入与类别数匹配的数组
- 数组元素之和应为1
- 示例:
- 二分类:[0.3, 0.7]
- 三分类:[0.2, 0.3, 0.5]
- 应用场景:
- 当已知各类别的真实分布时
- 例如:根据历史数据已知某疾病在人群中阳性率为5%
## force_alpha
**作用**:是否强制保持 alpha的原始值(即使接近0),默认为 False
**工作机制**:
- False(默认):
- 当alpha接近0时会自动调整为1e-10
- 避免数值计算不稳定
- True:
- 严格保持用户设置的alpha值
- 需要用户自行确保数值稳定性
五、代码实例
我们将使用scikit-learn内置的load_digits手写数字数据集,该数据集包含:
- 1797个手写数字样本
- 每个样本是8×8像素的灰度图像(64维特征向量)
- 像素值范围为0-16(表示灰度强度)
- 共10个类别(数字0-9)
# 导入必要的库
import pandas as pd # 数据处理库(虽然本例未直接使用,但通常用于数据预处理)
from sklearn.naive_bayes import MultinomialNB # 多项式朴素贝叶斯分类器
from sklearn.model_selection import train_test_split # 数据集划分工具
from sklearn.datasets import load_digits # 手写数字数据集
from sklearn.metrics import classification_report # 分类评估报告
# 加载内置手写数字数据集(每个样本是8x8像素的图像,共10类数字0-9)
# 注意:MultinomialNB通常用于离散计数数据,此处像素值被强制视为计数(可能需归一化)
digits = load_digits()
# 获取特征矩阵x和标签向量y
# x.shape=(n_samples,64), y.shape=(n_samples,)
x, y = digits.data, digits.target
# 划分训练集和测试集(70%训练,30%测试,random_state固定随机种子保证可复现性)
x_train, x_test, y_train, y_test = train_test_split(
x, y,
test_size=0.3,
random_state=42 # 固定随机种子确保每次划分结果一致
)
# 初始化多项式朴素贝叶斯模型
# 参数说明:
# - alpha=1.0:拉普拉斯平滑参数,防止零概率问题(默认值)
# - fit_prior=True:学习类别先验概率(根据数据分布自动计算)
# - class_prior=None:不手动指定先验概率[7](@ref)
model = MultinomialNB()
# 训练模型:计算每个类别的特征概率分布(多项式分布参数)
# 注意:此处像素值被当作离散计数处理,可能需先归一化为整数[7](@ref)
model.fit(x_train, y_train)
# 使用训练好的模型对测试集进行预测
y_pred = model.predict(x_test)
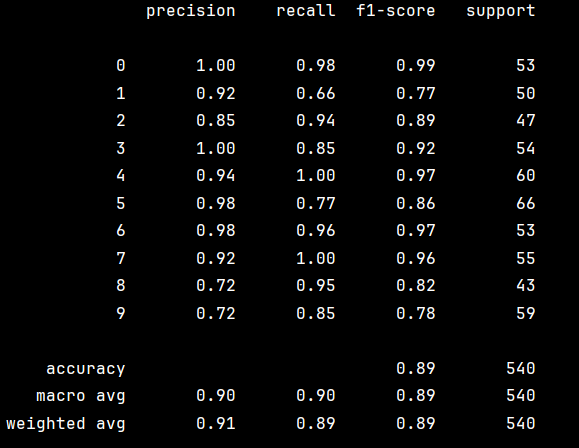
# 生成分类评估报告,包含以下指标:
# - precision:预测为某类的样本中实际正确的比例
# - recall:实际为某类的样本中被正确预测的比例
# - f1-score:precision和recall的调和平均数
# - support:测试集中每类的样本数[4](@ref)
print(classification_report(y_test, y_pred))