贪心+矩阵算法

贪心算法

贪心的本质是：选择每一阶段的局部最优，从而达到全局最优

做题的时候，只要想清楚 局部最优 是什么，如果推导出全局最优，其实就够了。

相减问题(怎么相减利润最大化)

买卖股票的最佳实际

思路：如果第i天卖出股票，则最大利润为(该天的股价-前面天数中最小的股价)，然后与已知的最大利润比较，如果大于则更新当前最大利润的值

• 只要找到一个最低买入价 minPrice，然后在后面找到最大差价。

• 遍历价格数组，同时维护：

  • 当前最小价格 minPrice

  • 当前最大利润 maxProfit = max(maxProfit, prices[i] - minPrice)

class Solution {
    public int maxProfit(int[] prices) {
        // 初始化最大利润为0，最低价格为第一个价格
        int maxProfit = 0;
        int minPrice = 100000;

        // 遍历价格数组
        for (int price : prices) {
            // 更新最低价格
            minPrice = Math.min(minPrice, price);
            // 更新最大利润
            maxProfit = Math.max(maxProfit, price - minPrice);
        }
        
        return maxProfit;
    }
}

买卖股票的最佳实际Ⅱ

遍历整个股票交易日价格列表 price，并执行贪心策略：所有上涨交易日都买卖（赚到所有利润），所有下降交易日都不买卖（永不亏钱）。

• 设 tmp 为第 i-1 日买入与第 i 日卖出赚取的利润，即 tmp = prices[i] - prices[i - 1] ；
• 当该天利润为正 tmp > 0，则将利润加入总利润 profit；当利润为 0 或为负，则直接跳过；
• 遍历完成后，返回总利润 profit。

等价于每天都与前一天做交易，赚才去买

class Solution {
    public int maxProfit(int[] prices) {
        int profit = 0;
        for (int i = 1; i < prices.length; i++) {
            int tmp = prices[i] - prices[i - 1];
            if (tmp > 0) profit += tmp;
        }
        return profit;
    }
}

抵达问题(抵达范围内是否出现更大的抵达范围)

跳跃游戏

此处i比较“原本范围内出现的最大抵达值”，由原本起始点字母出现的最大抵达范围一直在更新

思路：就是从起点出发，能够达到的最大点位，如果小于抵达不了则错误

• 如果某一个作为 起跳点 的格子可以跳跃的距离是 3，那么表示后面 3 个格子都可以作为 起跳点
• 可以对每一个能作为 起跳点 的格子都尝试跳一次，把 能跳到最远的距离 不断更新
• 如果可以一直跳到最后，就成功了

class Solution {
    public boolean canJump(int[] nums) {
        int maxReach = 0; // 记录能到达的最远索引
        int n = nums.length;
        
        for (int i = 0; i < n; i++) {
            // 如果当前位置 i 已经超出最大可达范围，则说明无法继续前进
            if (i > maxReach) {
                return false;
            }
            // 更新最大可达范围
            maxReach = Math.max(maxReach, i + nums[i]);
            // 如果最大可达范围已经超过或等于最后一个索引，则返回 true
            if (maxReach >= n - 1) {
                return true;
            }
        }
        return false;
    }
}

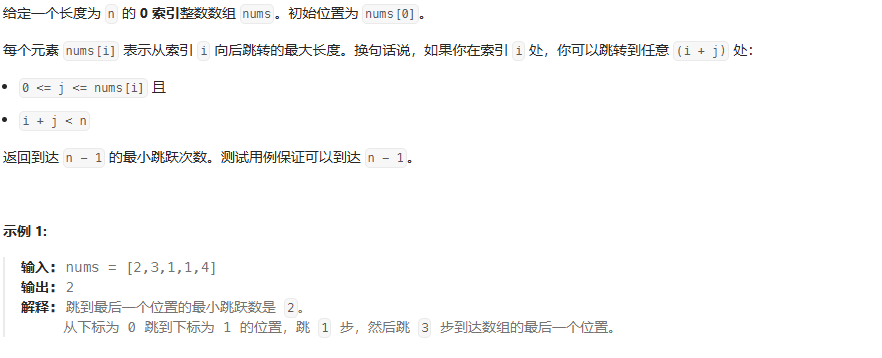
跳跃游戏Ⅱ（判断跳不跳）

此处i比较“原本出现范围的最大值”

思路：注意这个肯定是可以抵达到的 所以不需要判断 i > maxReach 无法抵达情况

可以这样想：判断当前节点能够抵达最大范围，在这范围内都要可以跳跃的，只有抵达范围边界，才会jumps加1， // 并选取当前节点抵达范围内的范围节点最大抵达范围，如果最大抵达范围大于nums.length长度，返回jumps

维护两个变量：

• curEnd：当前跳跃可达的最远边界。
• curFarthest：在当前跳跃范围内能到达的最远位置。

从左到右遍历数组（不包含最后一个元素，因为到达最后一个元素就结束）：

• 不断更新 curFarthest = max(curFarthest, i + nums[i])。
• 当 i 到达 curEnd 时，说明当前跳跃范围已经用完，需要增加一次跳跃次数 jumps++，并更新 curEnd = curFarthest。

如果 curEnd 已经到达或超过末尾，返回 jumps。

public int jump(int[] nums) {
    int jumps = 0;
    int curEnd = 0;
    int curFarthest = 0;

    for (int i = 0; i < nums.length - 1; i++) {
        curFarthest = Math.max(curFarthest, i + nums[i]);
        if (i == curEnd) { 
            jumps++;
            curEnd = curFarthest;
            if (curEnd >= nums.length - 1) {
                break;
            }
        }
    }
    return jumps;
}

划分字母区间

此处i比较“原本范围内出现的最大抵达值”，由原本起始点字母出现的最大抵达范围一直在更新

思路： 重复的字母只能出现在同一区间，那么建立字母表，记录字母出现的最大下表。就可以将问题转为抵达问题 // 即使在抵达范围内的元素出现了更大的抵达值，就直到指针到达该最大抵达值位置

   public List<Integer> partitionLabels(String s){
        char[] sChar = s.toCharArray();
        int n = s.length();
        int[] last = new int[26];
        for(int i = 0;i<n;i++){
            last[sChar[i] - 'a'] = i;// 每个字母出现的最后下标
        }

        List<Integer> ans = new ArrayList<>();
        int left = 0;
        int right = 0;
        for(int i =0;i<n;i++){
            right = Math.max(right,last[sChar[i]-'a']); // 当前字母可以抵达最大范围
            if(i == right){
                ans.add(right-left+1);
                left = right+1;
            }
        }
        return ans;

    }

矩阵

堆

数组中第K个最大元素

    public int findKthLargest(int[] nums, int k) {
        int n = nums.length;
        // 转换为找第n-k小的元素（从0开始）
        return quickselect(nums, 0, n - 1, n - k);
    }

    // 使用Hoare分区方案的快速选择算法
    private int quickselect(int[] nums, int left, int right, int k) {
        if (left == right) return nums[k]; // 基线条件

        // 随机选择pivot避免最坏情况
        int pivotIndex = left + new Random().nextInt(right - left + 1);
        int pivotValue = nums[pivotIndex];

        // 分区 每次循环只交换一次
        // 初始化左右指针
        int i = left - 1, j = right + 1;
        while (i < j) {
            // 从左找到第一个不小于pivot的元素
            do i++; while (nums[i] < pivotValue); // 先执行循环体，再检查条件
            // 从右找到第一个不大于pivot的元素
            do j--; while (nums[j] > pivotValue);

            // 交换这两个元素
            if (i < j) {
                int tmp = nums[i];
                nums[i] = nums[j];
                nums[j] = tmp;
            }
        }

        // 根据k的位置决定处理哪一部分
        // j停止的位置就是小于midValue范围
        if (k <= j) {
            return quickselect(nums, left, j, k);
        } else {
            return quickselect(nums, j + 1, right, k);
        }
    }

快排解法（随机选元素）

    private Random rand = new Random();

    public int findKthLargest (int[] nums,int k){
        int n = nums.length;
        return quickSelect(nums,0,n-1,n-k);
    }

    private int quickSelect(int[] nums,int left,int right,int targetIndex){
        int pivotIndex = partiton(nums,left,right);

        if(pivotIndex == targetIndex){
            return nums[pivotIndex];
        }else if(pivotIndex > targetIndex){
            return quickSelect(nums,left,pivotIndex-1,targetIndex);
        }else {
            return quickSelect(nums, pivotIndex+1, right, targetIndex);
        }
    }

    private int partiton(int[] nums,int left,int right){
        int pivotIndex = left + rand.nextInt(right-left+1); // 随机选取节点
        int pivotValue = nums[pivotIndex];  // 该节点值
        swap(nums,pivotIndex,right);  // 将该值放到末尾
        int storeIndex = left;
        for(int i = left;i<right;i++){ // 单指针划分小于/大于pivotValue区间
            if(nums[i]<pivotValue){
                swap(nums,storeIndex,i);
                storeIndex++;
            }
        }
        swap(nums,storeIndex,right); // 再把中位值互换回来
        return storeIndex;
    }

    private void swap(int[] nums,int i,int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

这个不太行，标准应该是快速排序

public int findKthLargest(int[] nums, int k) {
    // 1. 定义桶数组，大小 20001，表示存储 [-10000, 10000] 范围内的整数频率
    int[] buckets = new int[20001];
    int n = nums.length;

    // 2. 统计每个数字出现的次数
    for (int i = 0; i < n; i++) {
        // nums[i] + 10000 是为了将负数映射到 0~20000 的索引范围
        buckets[nums[i] + 10000]++;
    }

    // 3. 从大到小遍历桶（即从最大值到最小值）
    for (int i = 20000; i >= 0; i--) {
        // 每访问一个桶，就相当于从最大值开始往下数 k 个
        k -= buckets[i];
        if (k <= 0) {
            // 桶索引还原为原值：i - 10000
            return i - 10000;
        }
    }
    
    return 0; // 理论上不会走到这里
}

快速排序

递归+分区+互换值

// 分治快排
class QuickSort {
    public void quickSort(int[] nums, int left, int right) {
        if (left >= right) return; // 递归结束条件 索引

        int pivotIndex = partition(nums, left, right); // 找到 pivot 位置
        quickSort(nums, left, pivotIndex - 1);  // 排序左半部分
        quickSort(nums, pivotIndex + 1, right); // 排序右半部分
    }
    
    // 分区函数
    private int partition(int[] nums, int left, int right) {
        int pivot = nums[right]; // 选取最后一个元素作为 pivot
        int i = left; // i 指向比 pivot 小的区域的末尾

        for (int j = left; j < right; j++) {
            if (nums[j] < pivot) { // 如果当前元素比 pivot 小
                swap(nums, i, j);
                i++;
            }
        }
        swap(nums, i, right); // pivot 放到中间
        return i; // 返回 pivot 位置
    }
    // 交换值函数
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    // 测试
    public static void main(String[] args) {
        int[] arr = {3, 6, 8, 10, 1, 2, 1};
        QuickSort qs = new QuickSort();
        qs.quickSort(arr, 0, arr.length - 1);
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

栈

Stack<Integer> stack = new Stack<>();

有效括号

class Solution {
    public boolean isValid(String s) {
        //特殊情况
        if(s.isEmpty()){
            return true;
        }
        //创建栈，字符类型
        Stack<Character> stack = new Stack<Character>();
        
        for(char c:s.toCharArray()){

            if(c == '('){
                stack.push(')');
            }
            else if(c == '{'){
                stack.push('}');
            }
            else if(c=='['){
                stack.push(']');
            }
            // 要先判断是否为空，再判断出栈
            else if(stack.empty() || c!=stack.pop()){
                return false;
            }
        }

        if(stack.empty()){
            return true;
        }
        return false;
    }
}

每日温度

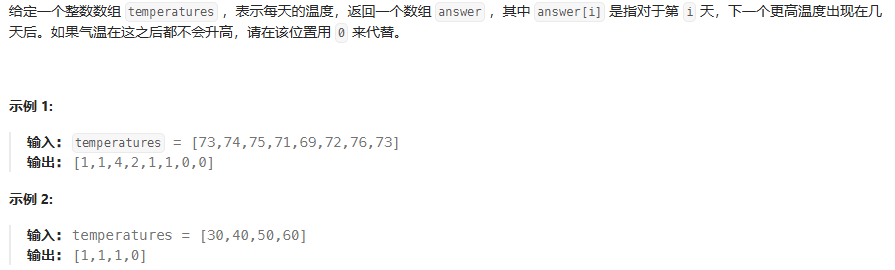
stack.peek() 返回栈顶元素，但不弹出（空栈会抛出异常）

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        int[] result = new int[n];
        Stack<Integer> stack = new Stack<>(); // 单调递减栈，存索引

        for (int i = 0; i < n; i++) {
            // 如果当前温度比栈顶索引的温度高，则计算等待天数
            while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                int prevIndex = stack.pop();
                result[prevIndex] = i - prevIndex;
            }
            // 当前索引入栈
            stack.push(i);
        }
        
        return result;
    }
}