【LeetCode】单链表经典算法：移除元素，反转链表，约瑟夫环问题，找中间节点，分割链表

问题一：删除链表中特定值节点

（一）问题描述

给定链表头节点head和整数val，删除所有值等于val的节点，返回新头节点。

示例1：

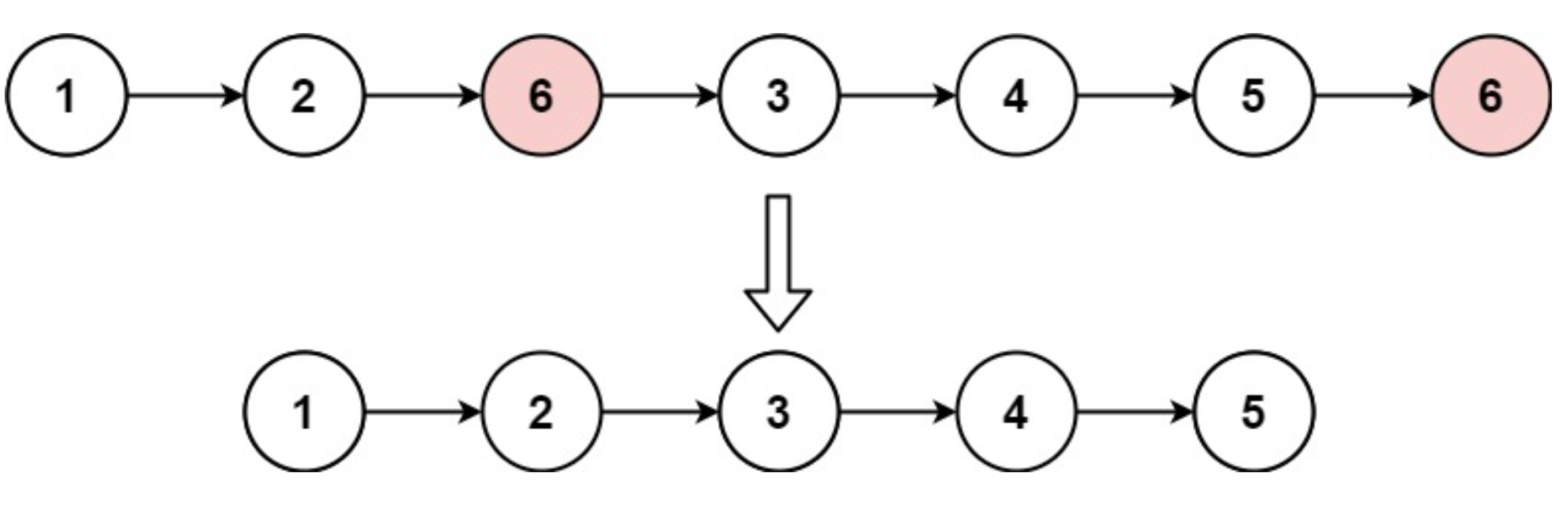
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：
输入：head = [], val = 1
输出：[]

示例 3：
输入：head = [7,7,7,7], val = 7
输出：[]

（二）解题思路

• 哨兵节点辅助：由于头节点可能被删除，创建哨兵节点dummy，其next指向原头节点。这样，头节点和其他节点的删除操作可统一处理。
• 遍历与删除：用指针cur从哨兵节点开始遍历，若cur->next节点值等于val，则跳过该节点（cur->next = cur->next->next ）；否则，移动cur指针继续遍历。

（三）代码实现

ListNode* removeElements(ListNode* head, int val) {
    ListNode dummy;
    dummy.next = head;
    ListNode* cur = &dummy;
    while (cur->next != NULL) {
        if (cur->next->val == val) {
            ListNode* temp = cur->next;
            cur->next = cur->next->next;
            free(temp); // 释放被删除节点内存，避免内存泄漏
        } else {
            cur = cur->next;
        }
    }
    return dummy.next;
}

（四）代码解析

• dummy是哨兵节点，栈上分配，无需手动释放。通过它统一处理头节点删除情况。
• 遍历中，找到要删除节点时，先用temp保存，修改指针后释放内存，符合C语言内存管理要求。

问题二：反转链表

（一）问题描述

给定链表头节点，反转链表并返回新头节点。

示例1：

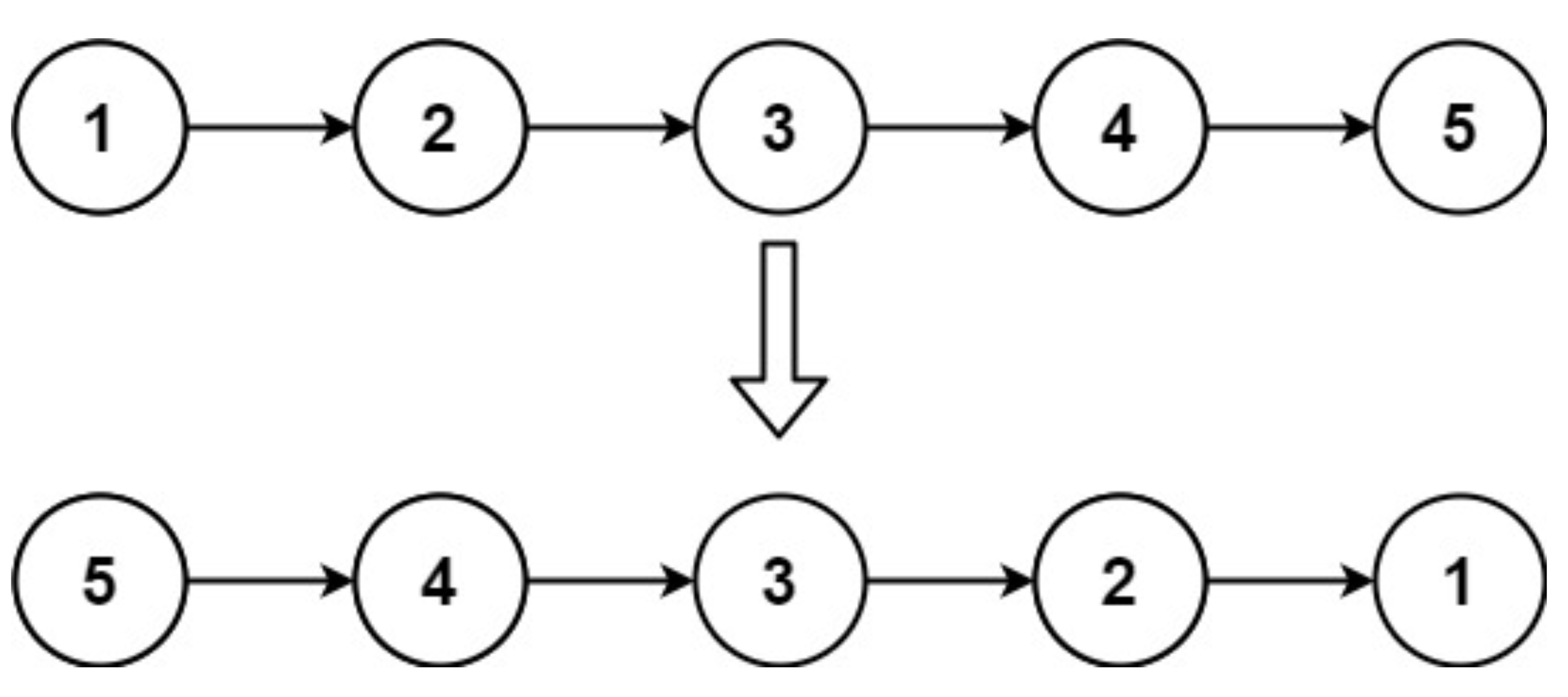
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例2：

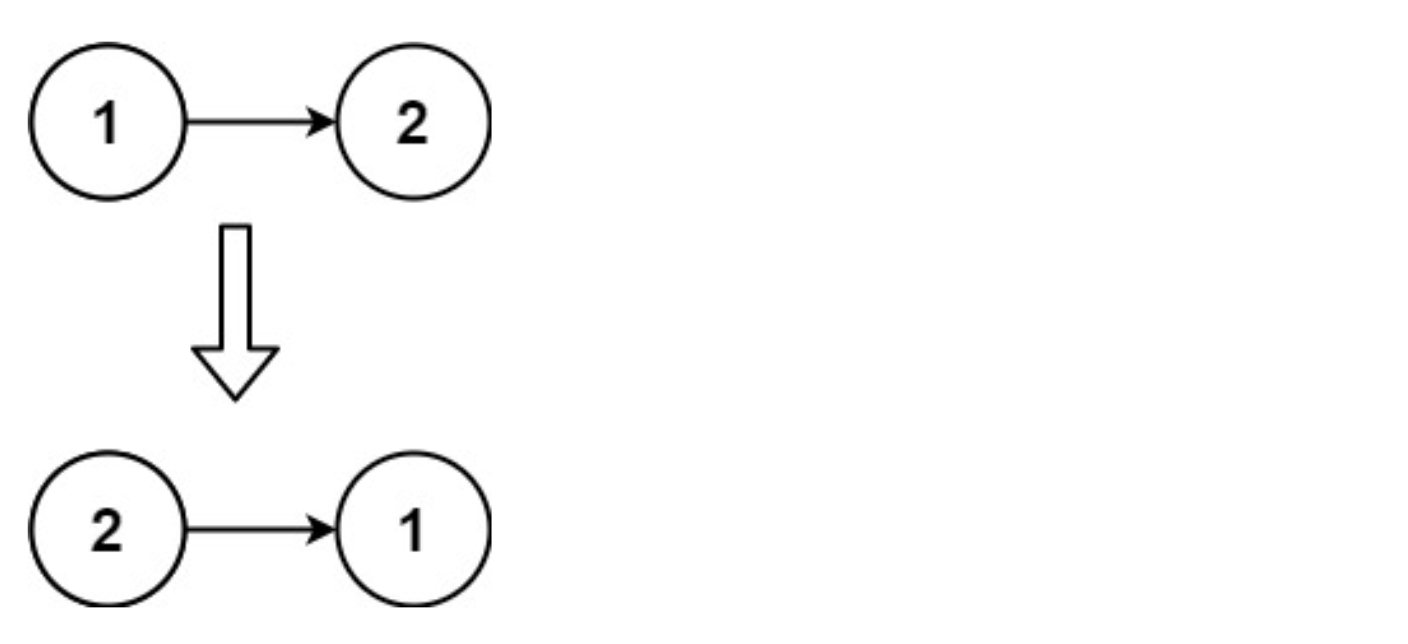
输入：head = [1,2]
输出：[2,1]

示例 3：
输入：head = []
输出：[]

（二）解题思路

• 双指针迭代：用prev（初始为NULL ）和cur（初始为头节点 ）两个指针。遍历中，保存cur->next，将cur->next指向prev完成反转，再更新prev和cur指针。

（三）代码实现

ListNode* reverseList(ListNode* head) {
    ListNode* prev = NULL;
    ListNode* cur = head;
    while (cur != NULL) {
        ListNode* nextTemp = cur->next;
        cur->next = prev;
        prev = cur;
        cur = nextTemp;
    }
    return prev;
}

（四）代码解析

• 每次循环先暂存cur的下一个节点nextTemp，避免反转后找不到后续节点。
• 逐步修改指针指向，完成链表反转，最终prev成为新头节点。

问题三：合并两个有序链表

（一）问题描述

将两个升序链表合并为一个新升序链表返回。

示例1：
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：
输入：l1 = [], l2 = []
输出：[]

示例 3：
输入：l1 = [], l2 = [0]
输出：[0]

（二）解题思路

• 哨兵节点简化：创建dummy节点，其next用于构建新链表。用cur指针遍历拼接。
• 比较与拼接：同时遍历两个链表，比较节点值，将较小值的节点接在cur后，并移动对应链表指针；某链表遍历完，直接拼接另一链表剩余部分。

（三）代码实现

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    ListNode dummy;
    dummy.next = NULL;
    ListNode* cur = &dummy;
    while (l1 != NULL && l2 != NULL) {
        if (l1->val < l2->val) {
            cur->next = l1;
            l1 = l1->next;
        } else {
            cur->next = l2;
            l2 = l2->next;
        }
        cur = cur->next;
    }
    cur->next = (l1 != NULL) ? l1 : l2;
    return dummy.next;
}

（四）代码解析

• dummy在栈上，方便管理。cur始终指向新链表当前末尾节点，用于拼接。
• 循环处理两链表都有节点的情况，最后拼接剩余节点，保证覆盖所有情况。

问题四：找链表中间节点

（一）问题描述

找到单链表中间节点，若有两个中间节点，返回第二个。

示例1：

输入：head = [1,2,3,4,5]
输出：[3,4,5]
解释：链表只有一个中间结点，值为 3 。

示例2:

输入：head = [1,2,3,4,5,6]
输出：[4,5,6]
解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。

（二）解题思路

• 快慢指针法：快指针fast每次走两步，慢指针slow每次走一步。当fast走到末尾（fast或fast->next为NULL ），slow指向中间节点。

（三）代码实现

ListNode* middleNode(ListNode* head) {
    ListNode* slow = head;
    ListNode* fast = head;
    while (fast != NULL && fast->next != NULL) {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}

（四）代码解析

• 利用快慢指针速度差，保证遍历结束时slow位置符合要求。无需额外空间，时间复杂度O(n) 。

问题五：链表分割（按值分区）

（一）问题描述

给定链表头节点和特定值x，使所有小于x的节点在大于等于x节点之前，无需保留原相对位置。

示例1:

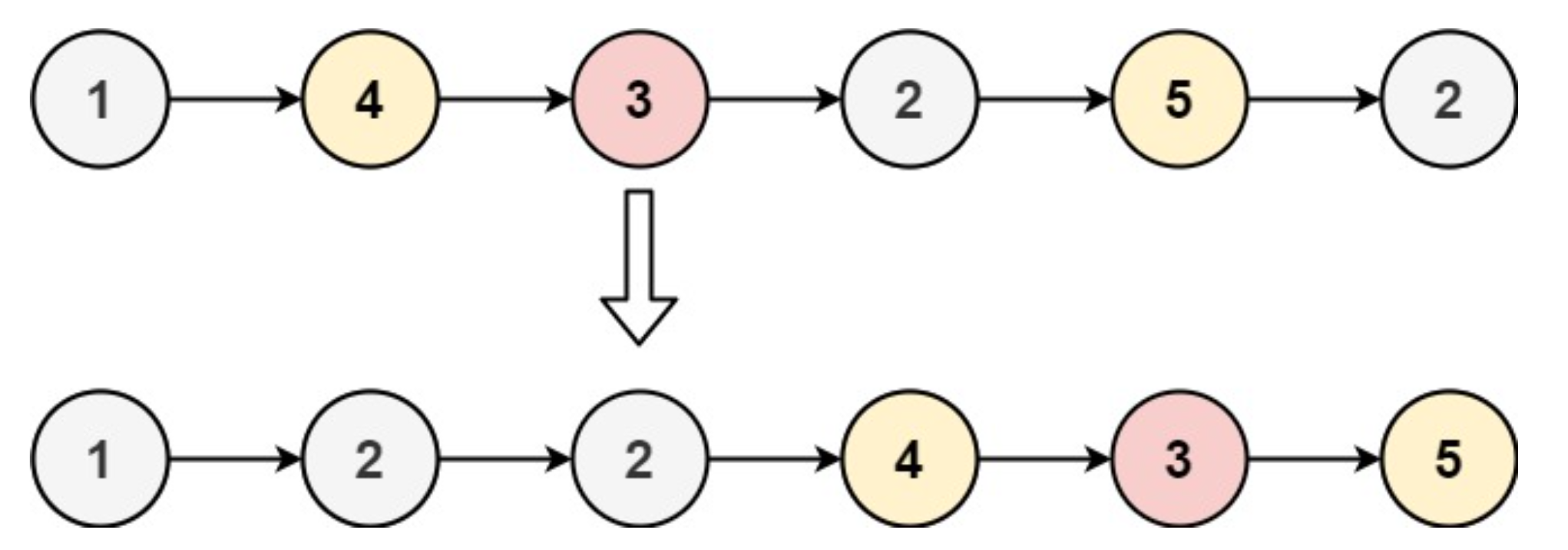
输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

示例 2：
输入：head = [2,1], x = 2
输出：[1,2]

（二）解题思路

• 双链表拆分：创建两个哨兵节点smallDummy和largeDummy，分别存储小于x和大于等于x的节点。遍历原链表，按值分配节点到对应链表，最后拼接两个链表。

（三）代码实现

ListNode* partition(ListNode* head, int x) {
    ListNode smallDummy, largeDummy;
    smallDummy.next = NULL;
    largeDummy.next = NULL;
    ListNode* smallCur = &smallDummy;
    ListNode* largeCur = &largeDummy;
    while (head != NULL) {
        if (head->val < x) {
            smallCur->next = head;
            smallCur = smallCur->next;
        } else {
            largeCur->next = head;
            largeCur = largeCur->next;
        }
        head = head->next;
    }
    largeCur->next = NULL; // 断开large链表末尾，避免环
    smallCur->next = largeDummy.next;
    return smallDummy.next;
}

（四）代码解析

• 两个哨兵节点在栈上，分别构建两个子链表。遍历后，处理large链表末尾（置NULL ），再拼接，得到符合要求的新链表。

问题六：约瑟夫环问题

（一）问题描述

n个人围成圈，从第1人开始报数，报到m的人离开，最后留下的人编号是多少。

示例1
输入：5,2
返回值：3
说明：开始5个人 1，2，3，4，5 ，从1开始报数，1->1，2->2编号为2的人离开
1，3，4，5，从3开始报数，3->1，4->2编号为4的人离开
1，3，5，从5开始报数，5->1，1->2编号为1的人离开
3，5，从3开始报数，3->1，5->2编号为5的人离开
最后留下人的编号是3

示例2
输入：1,1
返回值：1

（二）解题思路

• 数学推导（递推公式）：设f(n, m)为n人时最后存活者编号。递推关系f(n, m) = (f(n - 1, m) + m) % n ，初始条件f(1, m) = 0（编号从0开始方便计算，最后转换为题目要求的1 - n编号 ）。

（三）代码实现

int lastRemaining(int n, int m) {
    int res = 0;
    for (int i = 2; i <= n; i++) {
        res = (res + m) % i;
    }
    return res + 1; // 转换为1 - n编号
}

（四）代码解析

• 从i = 2开始递推，模拟人数从2到n的过程。最后+1是因为递推公式基于0开始编号，转换为题目要求的1 - n范围。

总结与拓展

通过这六个问题，我们深入练习了C语言中链表的各种操作，从基础的增删改查（删除、反转、合并等 ）到利用链表解决实际逻辑问题（分割 ），还接触了数学推导解决约瑟夫环的思路。

拓展建议：

• 尝试用递归方式实现反转链表、合并链表等操作，加深对递归的理解。
• 对于约瑟夫环问题，可尝试用链表模拟过程（虽然时间复杂度高，但能巩固链表操作 ），对比数学方法的效率差异。
• 思考这些算法在实际项目中的应用场景，比如链表分割在数据筛选、约瑟夫环在游戏开发中的逻辑控制等，让知识更好地落地。